博弈论

要想在现代社会做一个有文化的人，你必须对博弈论有一个大致了解。

简介

博弈论作为运筹学的一个分支，是一门以数学为基础，研究发生对抗与冲突时如何选择最优策略的学问。在我国，博弈论也被称为对策论。
游戏中何时出致胜的一招：不仅依赖自身的行为，还取决于对手的行动。
所有科学，不过是日常思考的提炼而已。——爱因斯坦
博弈论应是“交互的决策论”。——罗伯特 奥曼（2005年诺贝尔经济学奖获得者）
博弈论是交互式条件下“最优理性决策”。
博弈的精髓在于基于系统思维基础上的理性换位思考。
一种重要的思维模式：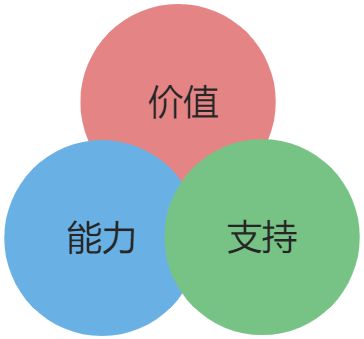

• 价值判断（知彼）；
• 能力判断（知己）；
• 寻求支持（合作）。

选择是人生最大的智慧，在冲突局势下决策者如何选择最优策略是人们普遍关心的问题。
博弈论则为交互的决策提供了一个分析框架，它的应用远远超出了经济学的范畴，正在成为政治学、哲学、军事科学、生物学、法学、社会学等领域极其有用的分析工具。

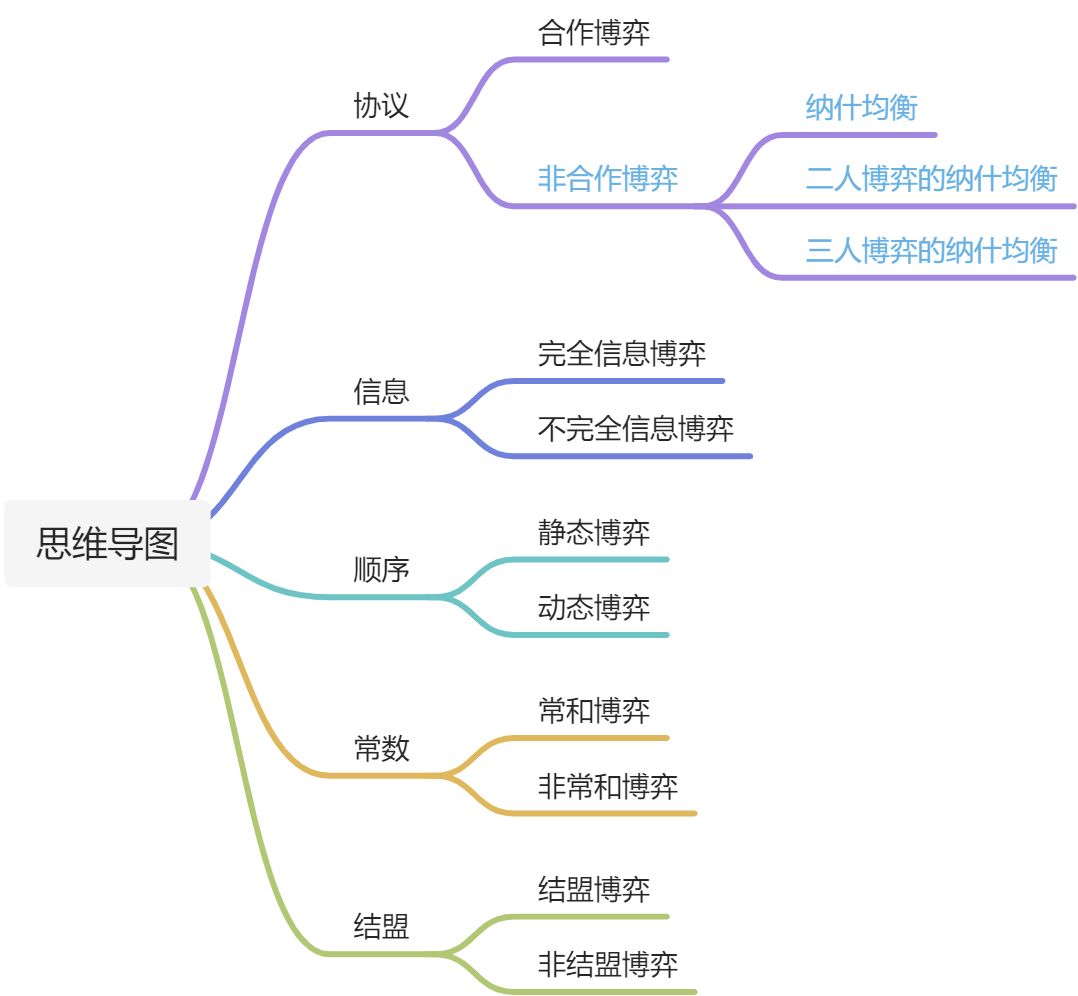
博弈论的分类

著名案例

囚徒困境

个人理性通过市场机制导致社会福利最优结论并不总是成立的！——>虽然“看不见的手”是有力的，但不是万能的。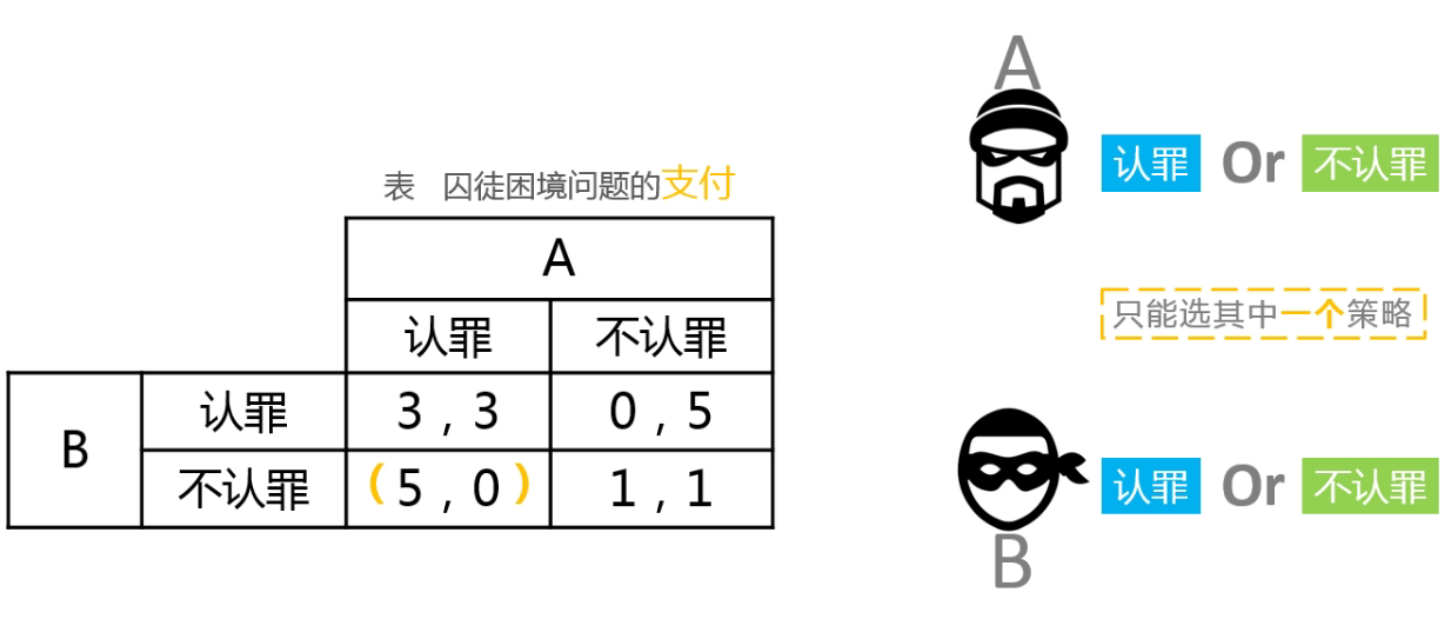

田忌赛马

博弈论的研究方法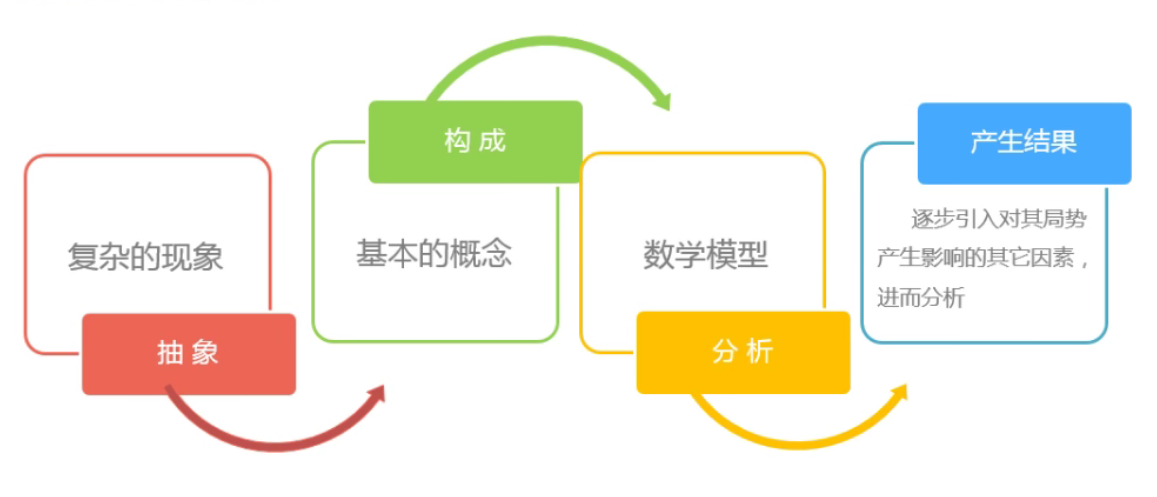

博弈论的基本假设：
个人理性：他必须并且能够充分考虑到人们之间行为的相互作用及其可能的影响，能够做出合乎理性的选择。

占优策略与占优策略均衡

在系统思维基础上，进行理性换位思考，采取最优策略，以最小代价取得最大利益。
均衡：在经济学中，稳定且可测的互动行为模式。
占优策略均衡：当一个博弈中的每一位参与者都选择了各自的占优策略时，相应的博弈结果就是占优策略均衡。不管所有其他参与人选择什么策略，这个参与人的占优策略都是他自己的最优策略。
纳什均衡：由所有参与人的最优策略组成的策略组合。此策略组合也被称为纳什均衡点。
合作均衡：各方协调行动，以求共同的支付最优化的策略而达到的结果。一般来说，如果博弈的参与者都能够履行协商后的策略，则他们选择的策略就构成了合作均衡。
纳什均衡：指的是这样一种策略组合，这种策略组合由所有参与人最优策略组成。
即在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动，因为局中的每一个博弈者都不可能因为单方面改变自己的策略而增加收益。

博弈分析的目标之一：找到博弈参与者之间稳定的、可预测的互动行为模式。

纳什均衡寻找方法：
关键：确定最优反应策略
方法步骤：

  1. 将收益矩阵中与每一策略的最优反应策略相应的收益数字标注下划线。
  1. 如果一个方框中的两个数字都被标注下划线下
  1. 这个方框对应的策略组合就是该博弈的一个纳什均衡

有些博弈不存在占有策略均衡，可能存在纳什均衡。 博弈论研究的是理性行为，这意味着每个局中人都会根据对手的策略选择自己的最优反应

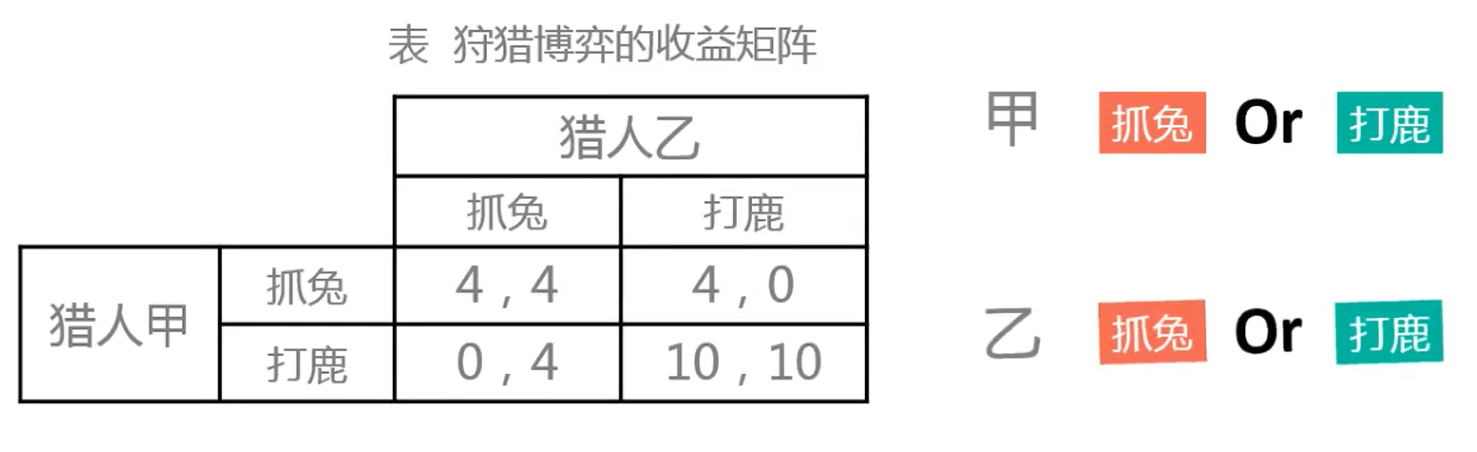
• 相对甲，乙的选择
  • 假设1：如果甲选择抓兔，乙最优选择是抓兔。
  • 假设2：如果甲选择打鹿，乙最优选择是打鹿。

则乙不存在占优策略。

• 相对乙，甲的选择
  • 假设1：如果乙选择抓兔，甲最优选择是抓兔。
  • 假设2：如果乙选择打鹿，甲最优选择是打鹿。

则乙不存在占优策略。
结论：

• 则表明此策略不存在占优策略均衡。
• 存在两个纳什均衡:（抓兔，抓兔)、(打鹿，打鹿)

多重纳什均衡：当一局博弈存在两个或两个以上的纳什均衡，就称为这局博弈存在多重纳什均衡。
纳什均衡的多重性问题：对于那些有多个纳什均衡存在的博弈而言，我们无法肯定地证明这个博弈的纳什均衡一定会出现，这也是博弈分析中真正的难题，通常称这个问题为纳什均衡的多重性问题。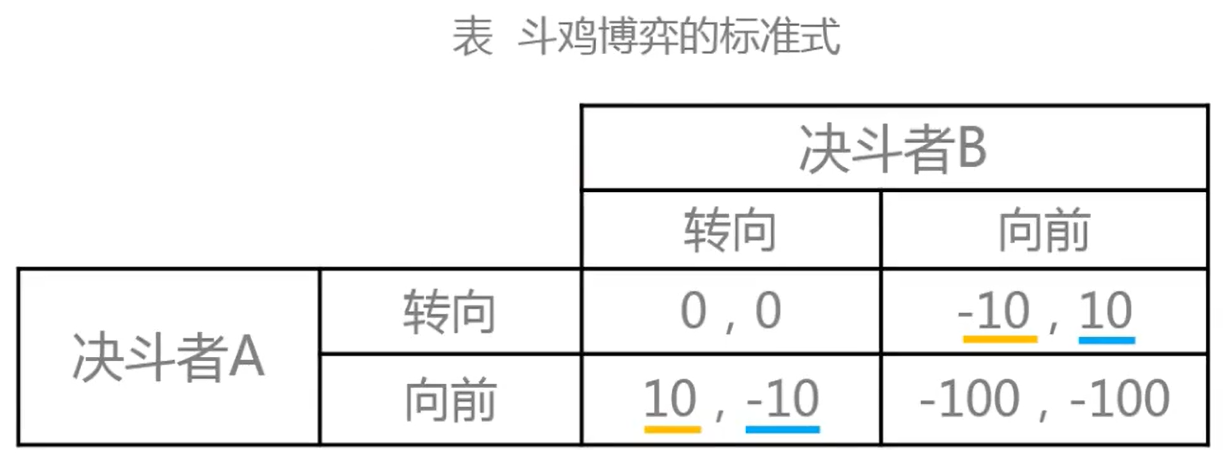

该博弈有两个纳什均衡：（向前，转向）与（转向，向前）即一个人向前，另一个人转向避让。

二人博弈的纳什均衡

零和博弈：零和博弈（zero-sum game），又称零和游戏，与非零和博弈相对，是博弈论的一个概念，属非合作博弈。它是指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”，故双方不存在合作的可能。
纯策略纳什均衡：是指在一个纯策略组合中,如果给定其他的策略不变，该节点不会单方面改变自己的策略，否则不会使节点访问代价变小。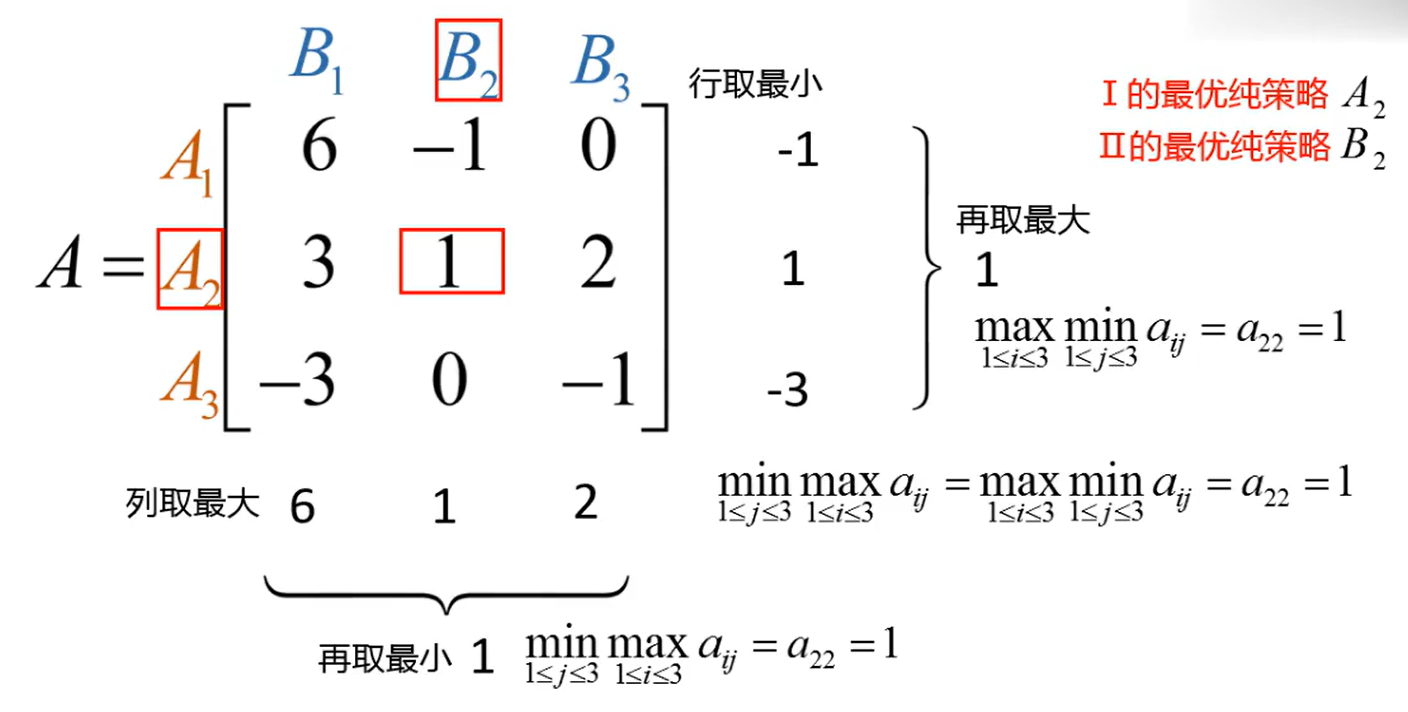

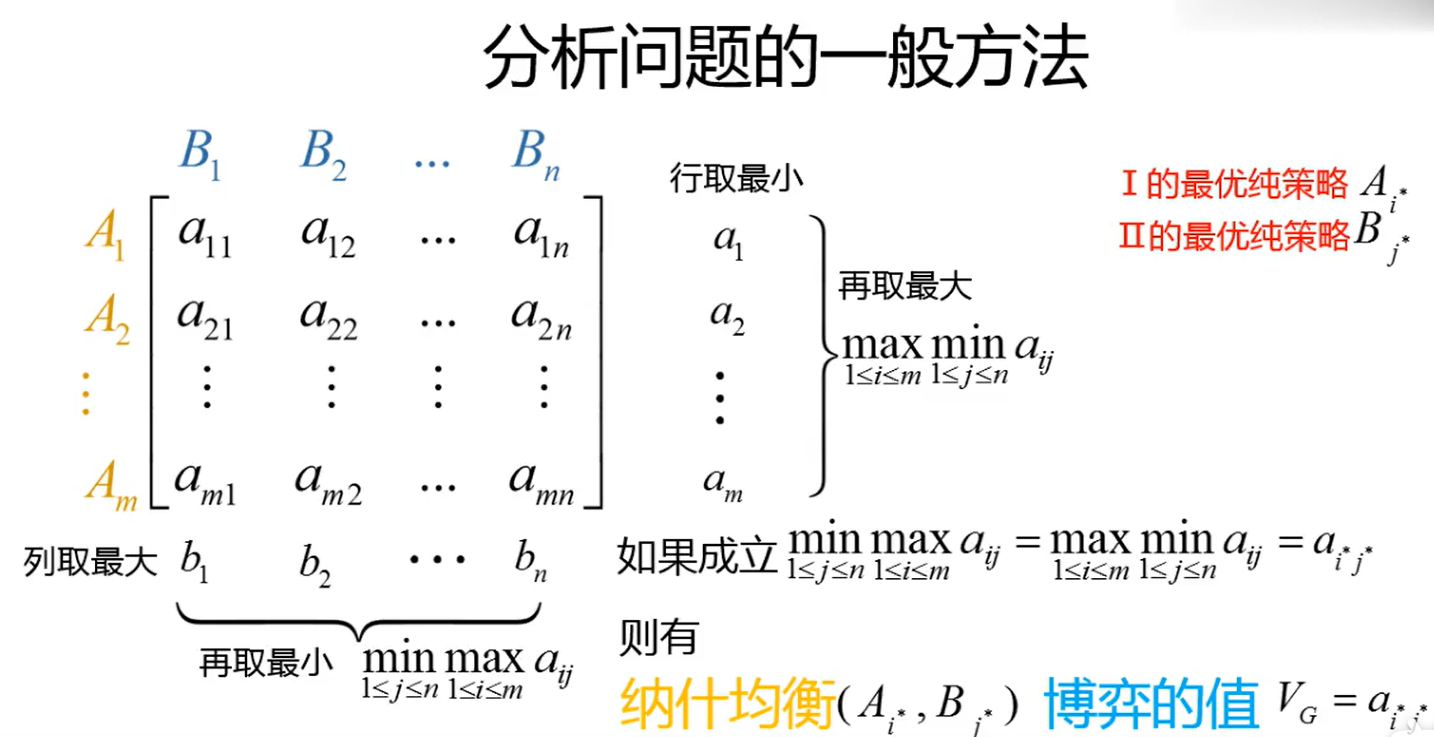
博弈在纯策略意义下的纳什均衡可以不唯一，博弈的值是唯一的

• 各方的收益或损失的总和不是零值；
• 局中人之间不再是完全对立；
• 一个局中人的所得并不是一定意味着其他局中人要同样数量的损失；
• 博弈参与者之间可能存在着某种共同的利益，可以“双赢”或“多赢”。

二人零和博弈的混合策略是以一定的概率在两个或多个纯策略中进行选择的策略。
任何一个给定的二人零和博弈一定存在混合策略下的纳什均衡。

奇数定理：几乎所有有限策略的博弈都有奇数个纳什均衡，包括纯策略纳什均衡和混合策略纳什均衡。