哈夫曼树

哈夫曼树是一种优化的树状结构。下面来介绍一下它。
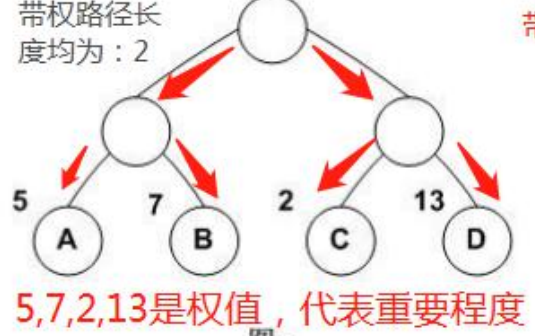
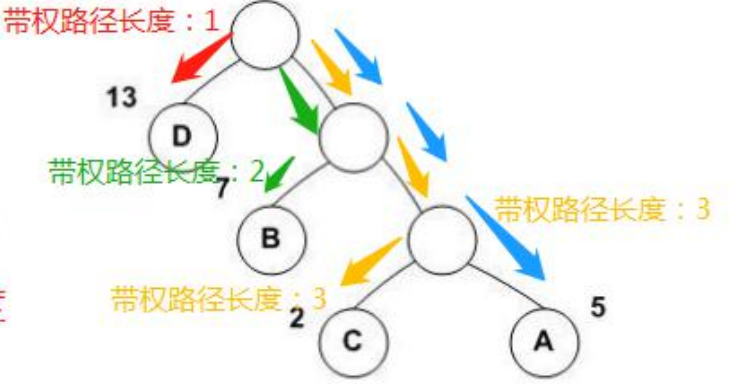
哈夫曼树是一种带权路径长度最短的二叉树，也被称为最优二叉树。我们可以把一个一个节点都看作带有权重的节点，然后某个节点到另一个节点若是可以直接相通，则带权路径长度为1，若是去某个节点需要经过1个节点，那带权路径长度即为2，以此类推。我们一般的网络状结构每层的各个节点的带权路径长度都是一样的，因为其为层状结构。如图所示，而哈夫曼树是一种通过改变各个节点带权路径长度以及安排权重不同的节点的位置使整个图的总带权路径长度最小。如图所示，第一幅图算出来的总带权路径长度为52，第二幅图算出来的总带权路径长度为48，说明第二个更简洁一些，这就是哈夫曼树的优化作用。假设我们有四个带权重的节点，哈夫曼树建立的过程是先把权重最大的两个先放在一边，代号分别是1和2（节点1权重大于节点2），拿出两个小权重节点（代号为3和4）排成并列，然后这两个小权重节点合并会生成一个新的权重节点（代号为5），这个节点置于这两个小权重节点的上方，然后我们在把节点2取出与节点5作合并，生成节点6，最后节点6与节点1作合并生成最上方的分叉节点0。那么生成那么哈夫曼树在词向量中能怎么应用呢？这时候我们可以将带有不同权重的节点看作是词，相应的权重可以看作是对应词出现的频率，我们每个节点都会用sigmoid函数做二分类，然后一层一层的做二分类，然后最后会得到很多值，每个值都是相应各个节点做二分类时得到的概率的连乘值，这些值加起来为1。说到这是不是很熟悉了，这就相当于做了一次softmax多分类，但是过程又不同，我们称之为分层softmax。