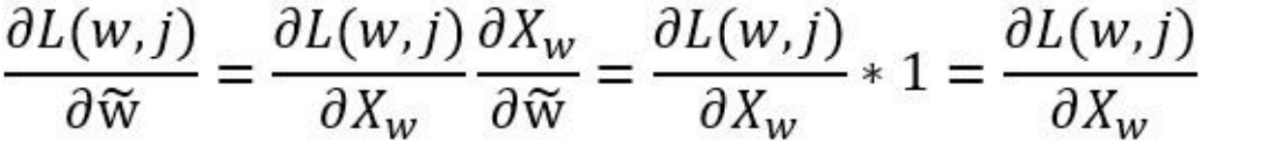哈夫曼树在CBOW模型上的应用

首先需要提出的是，哈夫曼树模型是一个分层的softmax模型，由于softmax一般应用在输出层，所以哈夫曼树模型也应该应用到输出层上。下面我们一起来探讨探讨哈夫曼树模型在CBOW模型上的应用。
CBOW模型的流程这里就不再赘述了，我们直接切入重点。还记得我们的CBOW模型在投影层之后输出的是什么吗，我们在投影层对上下文的词向量进行了加和求平均，因此投影层输出的是一个向量，这个向量包含了上下文词的所有信息。然后我们把这个向量看成根节点，正如我们上一节提到的哈夫曼树模型，我们需要一个根节点，然后根据这个根节点不断地做二叉树。每个节点分叉两个节点前需要做sigmoid二分类，然后会产生正例概率和负例概率，sigmoid函数的形式这里就不再赘述了。
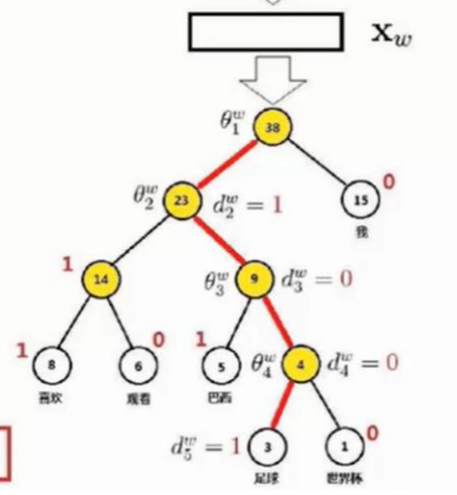
如图所示的过程，向左走为负例，向右走为正例，θ代表着节点前的参数向量，pw代表着路径，dw代表着pw路径上的第j个节点对应的编码，这个编码为0或者1。
如图所示我们第一次二分走的是负例，然后是正例，然后是正例，最后是负例，最后我们会得到一个概率值，这个概率值是经过的所有节点的概率的乘积。需要提出的是，经历的每个节点不一定走的全是正例方向，你有很大的可能走负例方向，这是需要特别提出的，只要我们最后输出的是正例就可以。我们把所有节点概率乘积称为最大似然函数，可以理解为使一系列事情全部发生的最大概率。由于乘积模式极其不容易求导，所以我们常常把最大似然函数转变成对数最大似然函数，这样可以有效地将乘积形式转换为加和形式，事实上，接下来的操作与我们推导交叉熵损失函数时并无二致，这里就不列出公式了。我们对损失函数求偏导，注意我们是对节点前的参数向量θ求偏导，这是需要特别提出的。我们对参数的更新使用的是随机梯度上升法，需要特别指出的是，我们需要更新两组参数，一组是进入投影层之前的look up table矩阵参数，一组参数是我们做哈夫曼树的时候节点前的参数θ，因此我们需要用链式求导法则求导，我们的损失函数先对θ求偏导，得到的Xw再对W求偏导。形式就是这样的，由于我们投影层做的运算是加和求平均的运算，不像往常的隐藏层一样做非线性变换，我们都该知道，加法求偏导是1，因此Xw对W的求导是1。我们由此得到梯度值，然后形式就像梯度下降公式一样，这里之所以叫做梯度上升是因为我们想使所有事件发生的概率达到最大，所以这里称作梯度上升，但是不论是梯度上升或是梯度下降，公式都是同一个，这点我们无需担心。
Skip-gram模型对哈夫曼树的应用和CBOW模型如出一辙，就不再赘述了。