leetcode150

题目

150 逆波兰表达式求值
根据 逆波兰表示法，求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：
输入：tokens = [“2”,”1”,”+”,”3”,”“]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) 3) = 9

思路

逆波兰表达式：是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

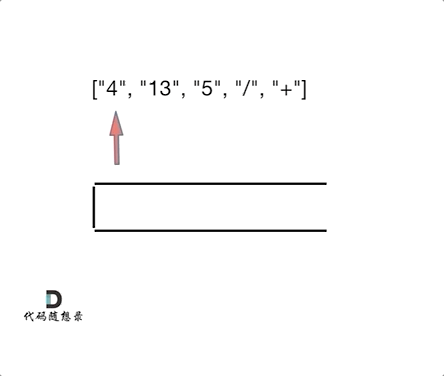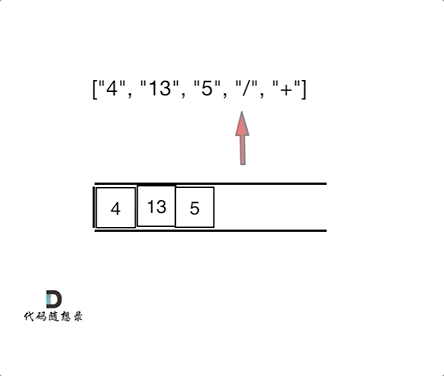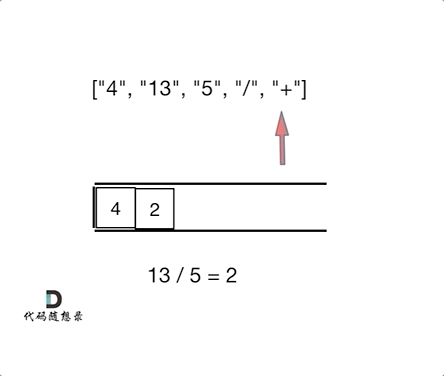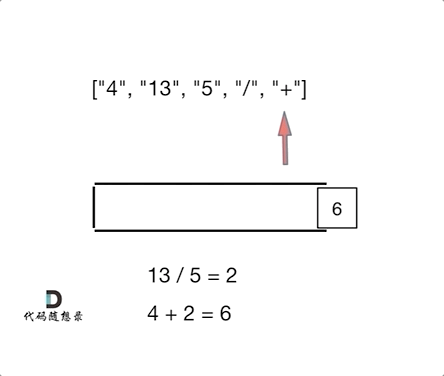
class Solution
{
public:
    int evalRPN(vector<string> &tokens)
    {
        std::stack<int> st;
        for (auto str : tokens)
        {
            if (str == "+")
            {
                int second = st.top();
                st.pop();
                int first = st.top();
                st.pop();
                st.push(first + second);
            }
            else if (str == "-")
            {
                int second = st.top();
                st.pop();
                int first = st.top();
                st.pop();
                st.push(first - second);
            }
            else if (str == "*")
            {
                int second = st.top();
                st.pop();
                int first = st.top();
                st.pop();
                st.push(first * second);
            }
            else if (str == "/")
            {
                int second = st.top();
                st.pop();
                int first = st.top();
                st.pop();
                st.push(first / second);
            }
            else //数字
            {
                st.push(std::stoi(str));
            }
        }
        return st.top();
    }
};