adaboost.py
元算法是对其他算法进行组合的一种方式。

bagging：自举汇聚法（bootstrap aggregating），在原始数据集中选取S次得到S个新数据集的方法。类似于放回取样。

boosting：集中关注被已有分类器错分的数据获得新的分类器。
bagging分类器的权重相等，而boosting中的分类器权重并不相等，每个权重代表分类器在上一轮迭代中的成功度。

AdaBoost是其中一种boosting算法。

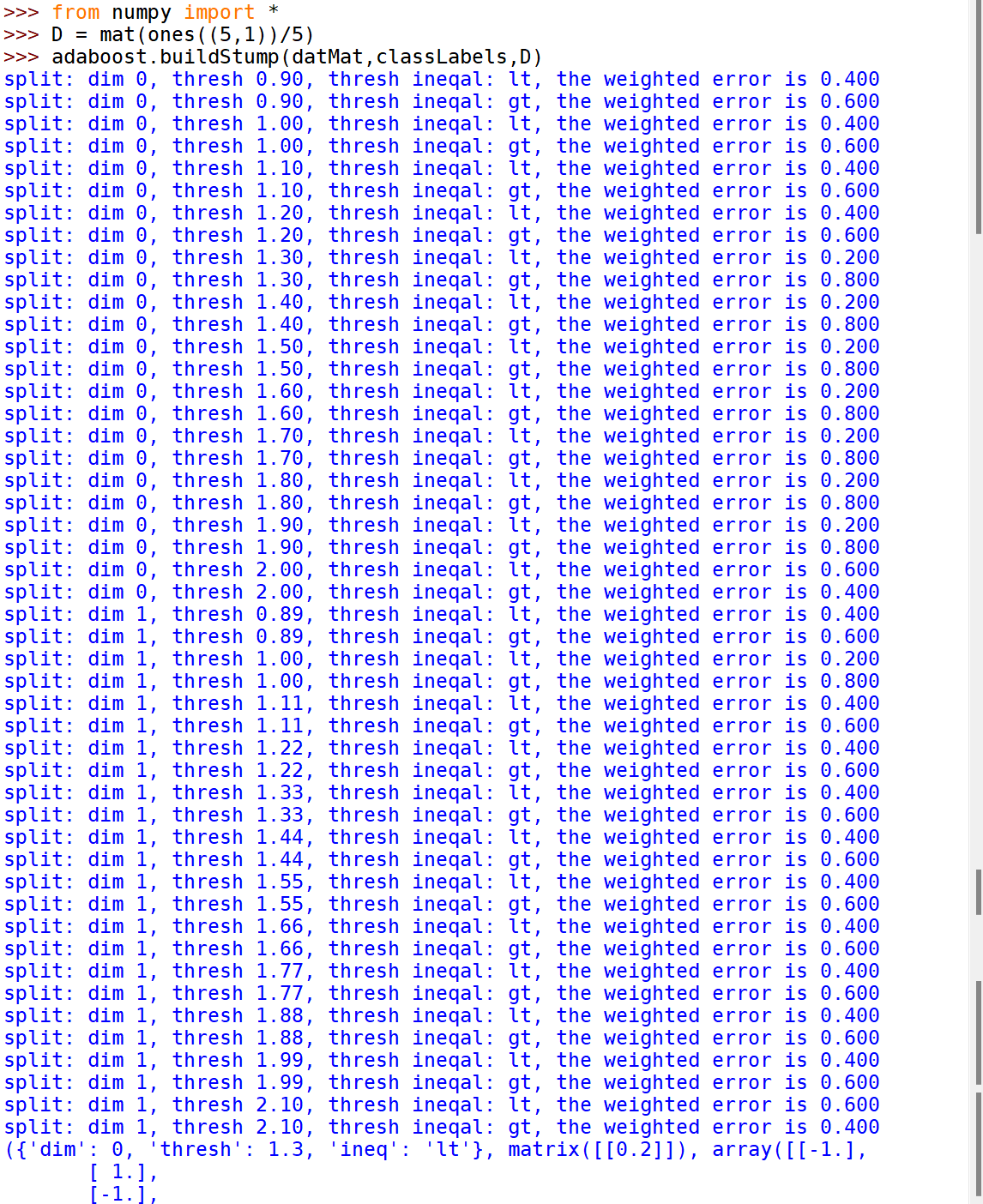
基于单层决策树构建弱分类器

只有单层，根据单个特征进行分类，因此类似于一个树桩。

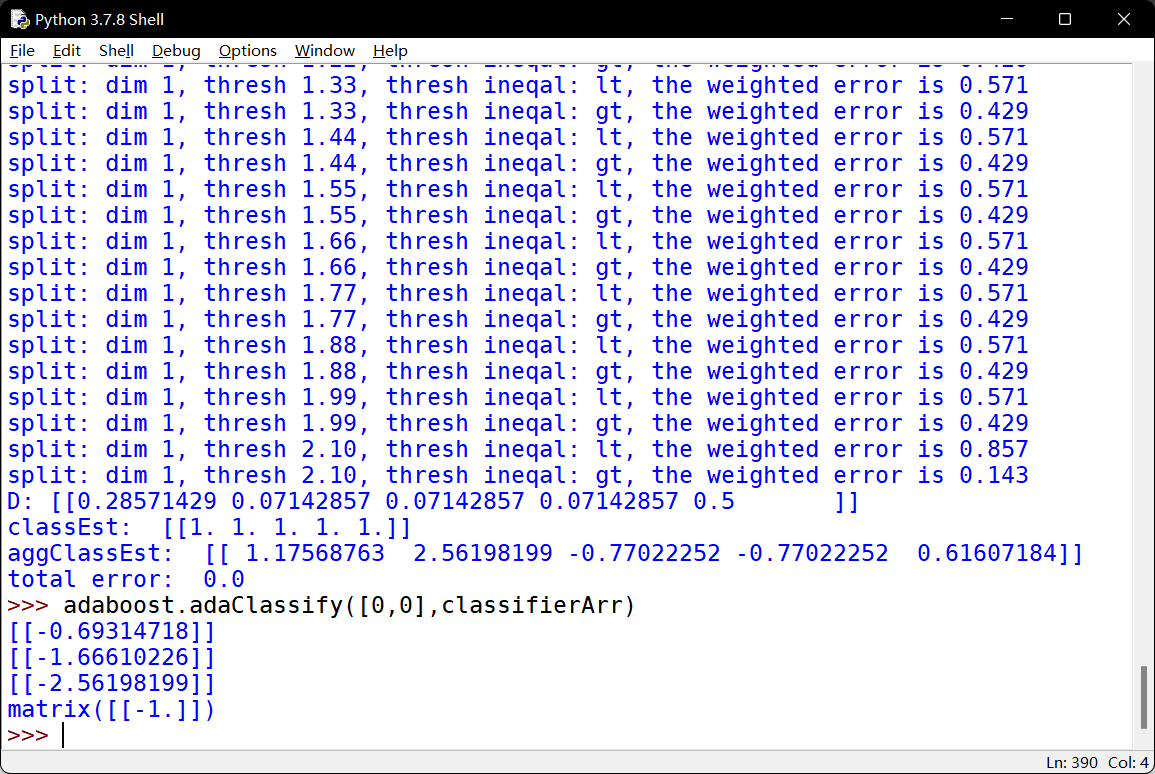
image.png

完整AdaBoost算法的实现

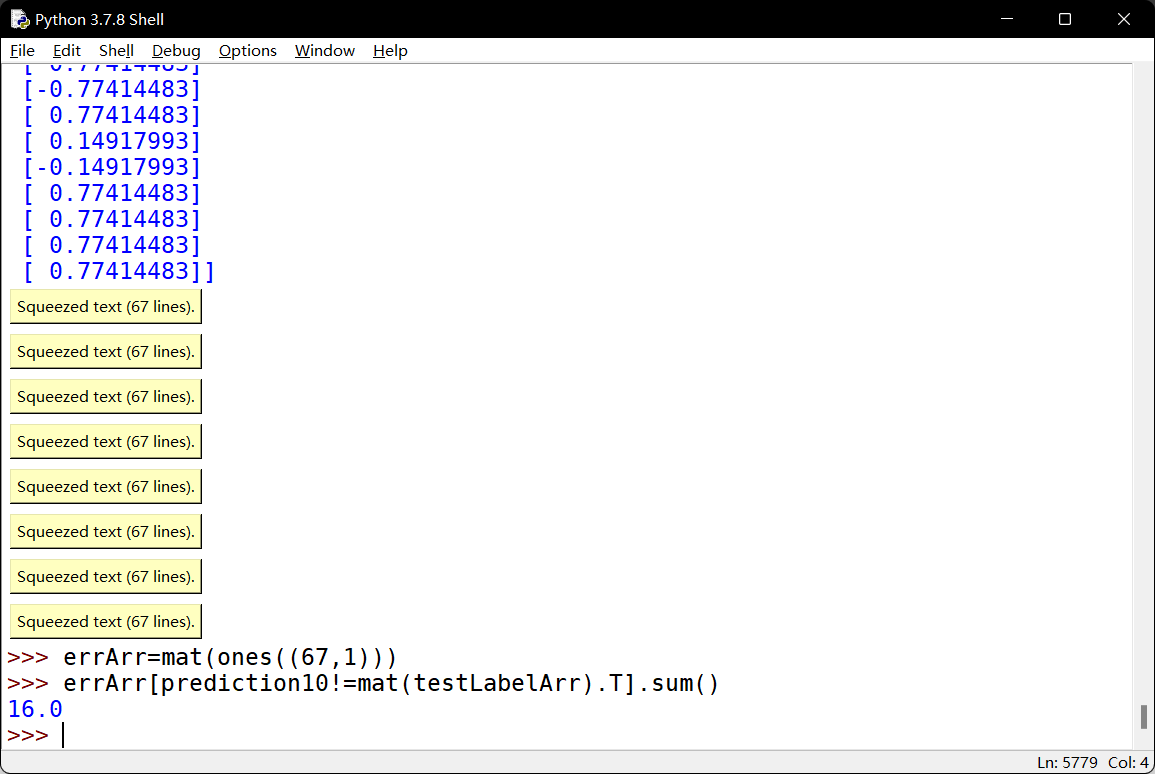
image.png
image.png
image.png

测试算法：基于AdaBoost的分类

image.png

示例：在一个难数据集上应用AdaBoost

image.png

非均衡分类的问题：

很多时候分类的代价并不相等，例如判断癌症

其他分类性能度量指标：正确率，召回率及ROC曲线

混淆矩阵：
真阳TP
真阴TN
假阳FP
假阴FN

正确率=TP/（TP+FP）
召回率=TP/（TP+FN）

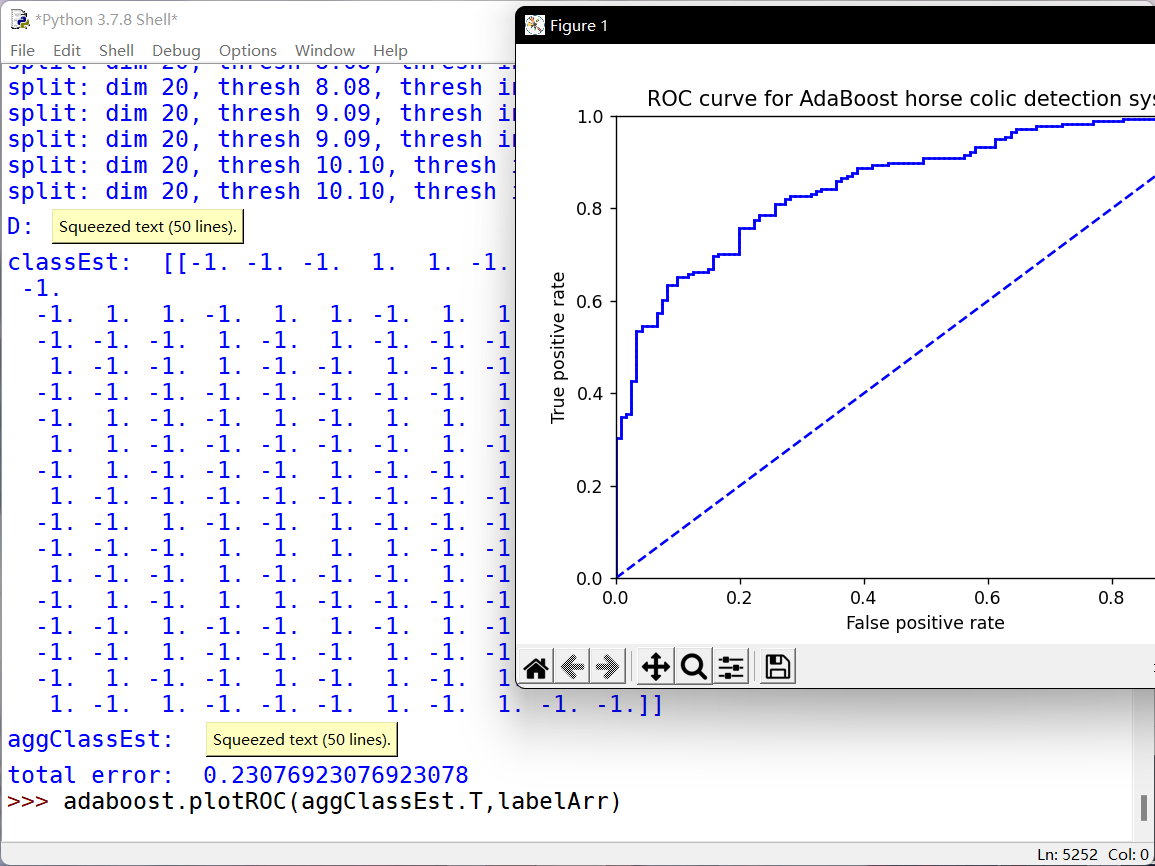
ROC曲线：当阈值变化时真阳率与假阳率的变化情况

AUC：在图线下面的面积大小。完美分类器的AUC为1.0,随机猜测的为0.5

  1. def plotROC(predStrengths, classLabels):
  2.     import matplotlib.pyplot as plt
  3.     cur = (1.0,1.0) #cursor
  4.     ySum = 0.0 #variable to calculate AUC
  5.     numPosClas = sum(array(classLabels)==1.0)
  6.     yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
  7.     sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
  8.     fig = plt.figure()
  9.     fig.clf()
  10.     ax = plt.subplot(111)
  11.     #loop through all the values, drawing a line segment at each point
  12.     for index in sortedIndicies.tolist()[0]:
  13.         if classLabels[index] == 1.0:
  14.             delX = 0; delY = yStep;
  15.         else:
  16.             delX = xStep; delY = 0;
  17.             ySum += cur[1]
  18.         #draw line from cur to (cur[0]-delX,cur[1]-delY)
  19.         ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
  20.         cur = (cur[0]-delX,cur[1]-delY)
  21.     ax.plot([0,1],[0,1],'b--')
  22.     plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
  23.     plt.title('ROC curve for AdaBoost horse colic detection system')
  24.     ax.axis([0,1,0,1])
  25.     plt.show()
  26.     print("the Area Under the Curve is: ",ySum*xStep)

image.pngimage.png