成都笨笨
博客园首页新随笔联系订阅 管理| | < | 2017年11月 | > |
| —- | —- | —- |
管理| | < | 2017年11月 | > |
| —- | —- | —- |
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 29 | 30 | 31 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
常用链接
- 我的随笔
- 我的评论
- 我的参与
- 最新评论
-
最新随笔
- 2. LBS之Geohash字符串编码
- 3. 身份证号码验证算法
- 4. 机器学习之寻找KMeans的最优K
- 5. 大数据系统之监控系统(二)Flume的扩展
- 6. 大数据系统之监控系统(一)
- 7. 大数据系统之系统设计
- 8. 机器学习的一些常用算法
- 9. Zookeeper(一)从抽屉算法到Quorum (NRW)算法
-
我的标签
算法(11)
- hive(8)
- 大数据(8)
- 搜索引擎(6)
- hive存储(5)
- hive的文件格式(4)
- PSO(4)
- 机器学习(4)
- 粒子算法(4)
- 日志监控(3)
-
随笔分类(36)
- hive安装配置(3)
- java(2)
- mahout(1)
- solr(1)
- 大数据(5)
- 机器学习(3)
- 十年老程序员找工作的经历(1)
- 搜索引擎(1)
- 搜索引擎手记(3)
- 算法(12)
-
随笔档案(31)
- 2016年6月 (5)
- 2016年5月 (1)
- 2015年12月 (9)
-
文章分类(14)
- hive(5)
- java(2)
- storm
-
文章档案(15)
- 2016年6月 (2)
- 2016年2月 (2)
- 2016年1月 (2)
-
hive
积分与排名
积分 -24334
排名 -14139
最新评论
- 1. Re:搜索引擎-一种提示词推荐算法
- 实现一个智能提示功能需要ajax、数据库、jsp/php、算法等很多知识,如果数据量大,还需要特殊优化一个小功能,花费太大精力很不划算92find.com上的一个js插件实现了搜索框自动补全托管服务,……
- —auo
- 2. Re:大数据系统之系统设计
- @Fredric_2013对…
- —成都笨笨
- 3. Re:大数据系统之系统设计
- 请问您这里PC\APP\WEB数据源,是指终端吗?是直接将终端的日志(比如Android或IOS)吐到kalfa集群?
- —Fredric_2013
- 4. Re:基于信息熵的无字典分词算法
- mark
- —tai君
- 5. Re:你真的说的清楚ArrayList和LinkedList的区别吗
- 有多大区别啊。就是一个链表一个数组,数据结构里面烂大街的东西了。封装了一下就不认识它们了么。
—安息茴香
阅读排行榜
- 2. 大数据系统之监控系统(一)(2186)
- 3. 算法(三)粒子群算法PSO的介绍(1720)
- 4. 机器学习之寻找KMeans的最优K(1614)
5. 大数据系统之监控系统(二)Flume的扩展(1532)
评论排行榜
- 2. 大数据系统之系统设计(2)
- 3. 搜索引擎-一种提示词推荐算法(1)
-
推荐排行榜
- 2. Solr5.0源码分析-SolrDispatchFilter(1)
- 3. 你真的说的清楚ArrayList和LinkedList的区别吗(1)
- 4. mapreduce导出MSSQL的数据到HDFS(1)
- 5. 机器学习之寻找KMeans的最优K(1)
机器学习之寻找KMeans的最优K
K-Means聚类算法是最为经典的,同时也是使用最为广泛的一种基于划分的聚类算法,它属于基于距离的无监督聚类算法。KMeans算法简单实用,在机器学习算法中占有重要的地位。对于KMeans算法而言,如何确定K值,确实让人头疼的事情。
最近这几天一直忙于构建公司的推荐引擎。对用户群体的分类,要使用KMeans聚类算法,就研究了一下。探索K的选择
对数据进行分析之前,采用一些探索性分析手段还是很有必要的。
对于高维空间,我们可以采用降维的方式,把多维向量转化为二维向量。好在,R语言包里提供了具体的实现,MDS是个比较好的方式。
多维标度分析(MDS)是一种将多维空间的研究对象简化到低维空间进行定位、分析和归类,同时又保留对象间原始关系的数据分析方法。R语言包提供了经典MDS和非度量MDS。
通过MDS对数据进行处理后,采用ggplot绘出点图,看看数据分布的情况,使得我们对要聚类的数据有个直观的认识。SSE和Silhouette Coefficient系数
我们还可以通过SSE和Silhouette Coefficient系数的方法评估最优K。譬如对K从1到15计算不同的聚类的SSE,由于kmeans算法中的随机因数,每次结果都不一样,为了减少时间结果的偶然性,对于每个k值,都重复运行50次,求出平均的SSE,最后绘制出SSE曲线。Silhouette Coefficient也采用同样做法。
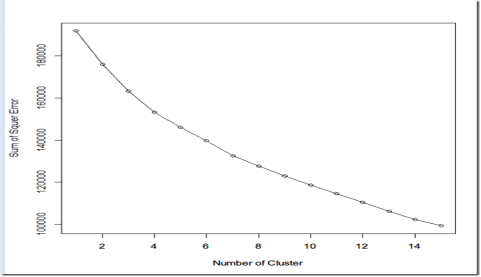
SSE结果
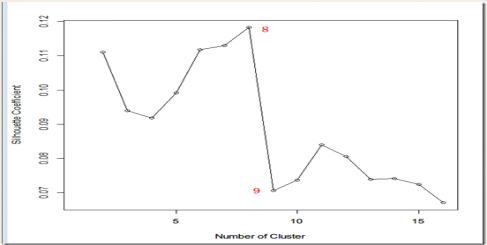
Silhouette Coefficient结果
从上图来看,8和9明显有一个尖峰。我们大体可以确定K的数目是8。值得注意在有些时候,这种方法有可能无效,但仍然不失为一个很好的方法。DB INDEX准则
DB INdex准则全称Davies Bouldin index 。类内离散度和类间聚类常被用来判断聚类的有效性,DB INdex准则同时使用了类间聚类和类内离散度。通过计算这个指数,来确定到底哪个Cluster最合理

R语言代码如下: 1 data <- read.csv(“a.csv”, header = T,
2
3 stringsAsFactors = F)
4 DB_index <- function(x, cl, k) {
5 data <- split.data.frame(x, cl$cluster)
6 # 计算类内离散度
7
8 S <- NULL
9 for (i in 1:k) {
10 S[i] <- sum(rowSums((data[[i]] - cl$centers[i])^2))/nrow(data[[i]])
11 }
12
13 # 计算类间聚类
14
15 D <- as.matrix(dist(cl$centers))
16
17 # 计算DB index
18
19 R <- NULL
20 for (i in 1:k) {
21 R <- c(max((S[i] + S[-i])/D[-i, i]), R)
22 }
23 DB <- sum(R)/k
24 return(DB)
25 }
26
27 # 循环计算不同聚类数的DB_Index指数
28
29 DB <- NULL
30 for (i in 2:15) {
31
32 cl <- kmeans(data, i)
33
34 DB <- c(DB_index(data, cl, i), DB)
35
36 }
37 plot(2:15, DB)
38 lines(2:15, DB)
1 data <- read.csv(“a.csv”, header = T,
2
3 stringsAsFactors = F)
4 DB_index <- function(x, cl, k) {
5 data <- split.data.frame(x, cl$cluster)
6 # 计算类内离散度
7
8 S <- NULL
9 for (i in 1:k) {
10 S[i] <- sum(rowSums((data[[i]] - cl$centers[i])^2))/nrow(data[[i]])
11 }
12
13 # 计算类间聚类
14
15 D <- as.matrix(dist(cl$centers))
16
17 # 计算DB index
18
19 R <- NULL
20 for (i in 1:k) {
21 R <- c(max((S[i] + S[-i])/D[-i, i]), R)
22 }
23 DB <- sum(R)/k
24 return(DB)
25 }
26
27 # 循环计算不同聚类数的DB_Index指数
28
29 DB <- NULL
30 for (i in 2:15) {
31
32 cl <- kmeans(data, i)
33
34 DB <- c(DB_index(data, cl, i), DB)
35
36 }
37 plot(2:15, DB)
38 lines(2:15, DB) ## CANOPY算法
Canopy聚类最大的特点是不需要事先指定k值(即clustering的个数),与其他聚类算法相比,Canopy聚类虽然精度较低,但其在速度上有很大优势。
## CANOPY算法
Canopy聚类最大的特点是不需要事先指定k值(即clustering的个数),与其他聚类算法相比,Canopy聚类虽然精度较低,但其在速度上有很大优势。
因此可以使用Canopy聚类先对数据进行“粗”聚类,得到k值后再使用K-means进行进一步“细”聚类。这个算法不多说了,mahout聚类里有具体实现。
参阅:https://en.wikipedia.org/wiki/Davies-Bouldin_index mahout大数据机器学习算法机器学习KMeansmahout好文要顶关注我收藏该文

 成都笨笨
成都笨笨
关注 - 4
粉丝 - 17+加关注10« 大数据系统之监控系统(二)Flume的扩展
» shell变量详解
2016-06-27 21:23成都笨笨16140编辑收藏刷新评论刷新页面返回顶部登录注册访问【推荐】50万行VC++源码: 大型组态工控、电力仿真CAD与GIS源码库
【活动】阿里云双11活动开始预热 云服务器限时2折起
【调查】有奖调研即刻参与,你竟然是酱紫程序猿!
【推荐】Vue.js 2.x 快速入门,大量高效实战示例
腾讯股价频创历史新高 马化腾重登中国首富宝座
乐视致新发公开信:让商业回归本质 业务不受外部影响
Skype视频面试服务更新加入群面和更多编程语言
逾8成企业雇员认为Face ID可靠,能取代密码
京东商城“跨界”住房租赁电商业务:正在收购域名
更多新闻…
改善程序员生活质量的 3+10 习惯
NASA的10条代码编写原则
为什么你参加了那么多培训,却依然表现平平?
写给初学前端工程师的一封信
实用VPC虚拟私有云设计原则
更多知识库文章…博客园沪江博客

