测试数据科学家聚类技术的40个问题（能力测验和答案）（下）

测试数据科学家聚类技术的40个问题（能力测验和答案）（下）

2017-03-24AI科技大本营> 【AI100 导读】本次测试的重点主要集中在概念、聚类基本原理以及各种技术的实践知识等方面。本文为下部，包括21-40题。上部请查看：

测试数据科学家聚类技术的40个问题（能力测验和答案）（上）

Questions & Answers

Q21. 给定具有以下属性的六个点：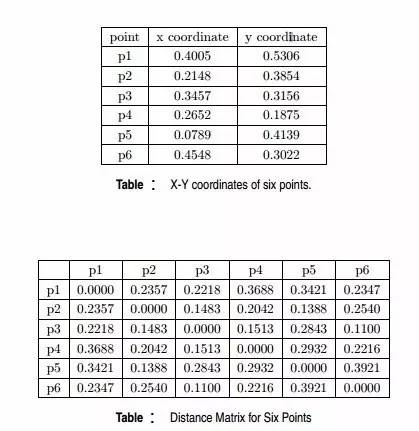


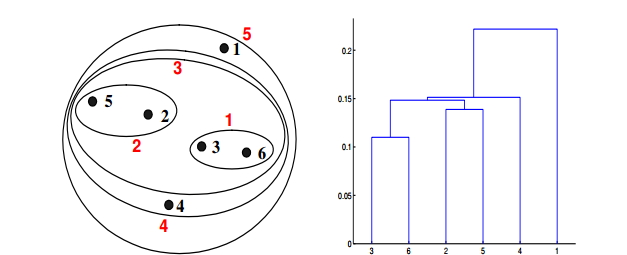
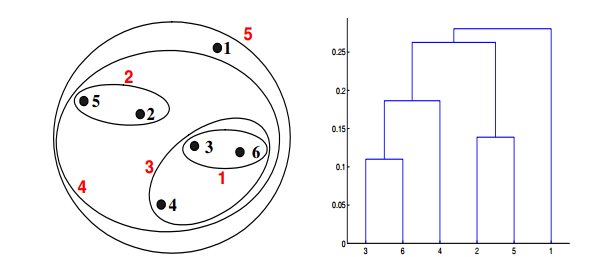
如果在层次聚类中使用组平均值接近函数，可以通过下面哪些聚类表示和树形图来描述？

答案：C

对于层次聚类的的群平均值，两个簇的接近度指的是不同集群中的每一对点对的近似值的平均值。这是最大值和最小值方法之间的中间方法，下面的等式可以表示：



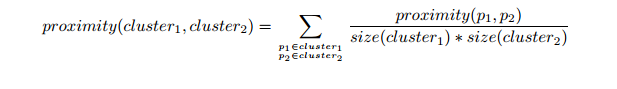
我们来计算一下某些簇之间的距离。dist({3, 6, 4}, {1}) = (0.2218 + 0.3688 + 0.2347)/(3 ∗ 1) = 0.2751，dist({2, 5}, {1}) = (0.2357 + 0.3421)/(2 ∗1) = 0.2889. dist({3, 6, 4}, {2, 5}) = (0.1483 + 0.2843 + 0.2540 + 0.3921 +0.2042 + 0.2932)/(6∗1) = 0.2637。因为dist({3, 6, 4}, {2, 5})小于dist({3, 6, 4},{1}) 和dist({2, 5}, {1})，所以这两个簇在第四阶段被合并到了一起。

Q22. 给定具有以下属性的六个点：


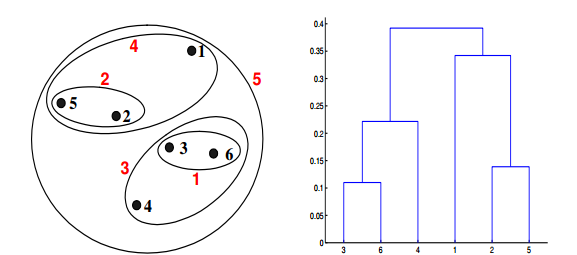
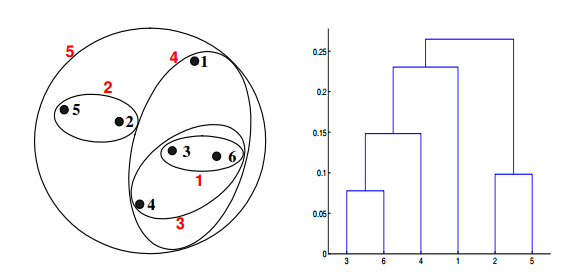
如果在层次聚类中使用 Ward 方法的接近函数，可以通过下面哪些聚类表示和树形图来描述？

答案：D

Ward 方法是一种质心算法。质心方法通过计算集群的质心之间的距离来计算两个簇的接近度。对于 Ward 方法来说，两个簇的接近度指的是当两个簇合并时产生的平方误差的增量。在6%的样本数据集中，使用 Ward 方法产生的结果和使用最大值、最小值、组平均值的聚类结果会有所不同。

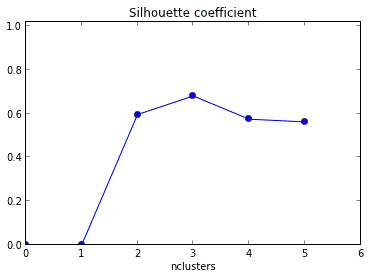
Q23. 根据下图，簇的数量的最佳选择是？

1. 1

2. 2

3. 3

4. 4

答案：C

轮廓系数旨在将某个对象与自己的簇的相似程度和与其他簇的相似程度进行比较。轮廓系数最高的簇的数量表示簇的数量的最佳选择。

Q24. 在聚类分析之前处理缺失值的有效迭代策略有哪些？

1. 平均值插补法

2. 由最近的值进行分配

3. 用期望最大化算法进行插补

4. 以上都是

答案：C

上面提到的所有方法都可以有效的在聚类分析之前处理缺失值，但是只有期望最大化算法是可以迭代的。

Q25. K均值算法有一些局限性。 其中的一个是，把一个点（完全属于一个集群或根本不属于一个集群的点）强制分配到一个集群。

注意：软性分配可以被认为是被分配给每个聚类的概率：例如 K= 3 时对于一些点 Xn，p1 = 0.7，p2 = 0.2，p3 = 0.1

下面哪些算法允许软性分配？**

1. 高斯模糊模型

2. 模糊K均值

选项：

1. 1

2. 2

3. 1 2

4. 以上都不是

答案：C

高斯模糊模型和模糊K均值都允许进行软性分配。

Q26. 假设你想使用K均值聚类算法将7个观测值聚类到3个簇中。在第一次迭代簇之后，C1、C2和C3具有以下观测值：

C1: {(2,2), (4,4), (6,6)}
C2: {(0,4), (4,0)}
C3: {(5,5), (9,9)}

如果继续进行第二次迭代，哪一个将成为集群的质心？

1. C1: (4,4), C2: (2,2), C3: (7,7)

2. C1: (6,6), C2: (4,4), C3: (9,9)

3. C1: (2,2), C2: (0,0), C3: (5,5)

4. 以上都不是

答案：A

找到集群中数据点的质心 C1 = ((2+4+6)/3,(2+4+6)/3) = (4, 4)
找到集群中数据点的质心 C2 = ((0+4)/2, (4+0)/2) =(2, 2)
找到集群中数据点的质心 C3 = ((5+9)/2, (5+9)/2) =(7, 7)
因此, C1: (4,4), C2: (2,2), C3: (7,7)

Q27. 假设你想用K均值聚类方法将7个观测值聚类到3个簇中，在第一次迭代簇之后，C1、C2、C3具有以下观测值：

C1: {(2,2), (4,4), (6,6)}
C2: {(0,4), (4,0)}
C3: {(5,5), (9,9)}

在第二次迭代中，观测点（9，9）到集群质心C1的 Manhattan 距离是？

1. 10

2. 5 * sqrt（2）

3. 13 * sqrt（2）

4. 以上都不是

答案：A

（4,4）和（9,9）的 Manhattan 距离是：（9-4）+（9-4）= 10。

Q28. 如果聚类分析现在有两个变量V1和V2，对于K均值分析（k=3）的描述，下面哪些是正确的？
**

1. 如果V1和V2完全相关，簇的质心会在一条直线上

2. 如果V1和V2完全不相关，簇的质心会在一条直线上

选项：

1. 1

2. 2

3. 1 2

4. 以上都不是

答案：A

如果变量V1和V2完全相关，那么所有的数据点都会在同一条直线上，三个簇的质心也会在同一条直线上。

Q29. 应用K均值算法之前，特征缩放是一个很重要的步骤。这是为什么呢？

1. 在距离计算中，它为所有特征赋予相同的权重

2. 不管你用不用特征缩放，你总是会得到相同的簇

3. 在Manhattan距离中，这是重要的步骤，但是Euclidian中则不是

4. 以上都不是

答案：A

特征缩放保证了在聚类分析中每一个特征都有同样的权重。想象这样一个例子，对体重范围在55-100（kg）和身高在5.6到6.4（英寸）的人进行聚类分析。因为体重的范围远远高于身高的范围，如果不进行缩放，产生的簇会对结果产生误导。因此，使它们具有相同的级别就显得很有必要了，只有这样才能保证聚类结果权重相同。

Q30. 为了在K均值算法中找到簇的最优值，可以使用下面哪些方法？

1. Elbow 法

2. Manhattan 法

3. Ecludian 法

4. 以上都是

5. 以上都不是

答案：A

在上面给出的选项中，只有 Elbow 方法是用来寻找簇数的最优值的。方差百分比是一个与簇数有关的函数，Elbow 方法关注的就是方差百分比：分析时应该选择多个簇，以便在添加另一个簇时，不会给出更好的数据建模。

Q31. 关于K均值聚类的描述正确的是？
**

1. K均值对簇中心初始化非常敏感

2. 初始化不良会导致收敛速度差

3. 初始化不良可能导致整体聚集不良

选项：

1. 1 3

2. 1 2

3. 2 3

4. 1 2 3

答案：D

上面给出的三个描述都是正确的。K均值对簇中心初始化非常敏感。而且，初始化不良会降低收敛的速度差并会使得整体聚集效果不佳。

Q32. 可以用下面哪一种方法来获得和全局最小值有关的K均值算法的良好结果？
**

1. 试着运行不同的质心初始化算法

2. 调整迭代的次数

3. 找出最佳的簇数

选项：

1. 2 3

2. 1 3

3. 1 2

4. 以上都是

答案：D

上面列举的所有选项都是为了获得良好的聚类结果而采用的标准实践。

Q33. 根据下图的结果，簇的数量的最好选择是？**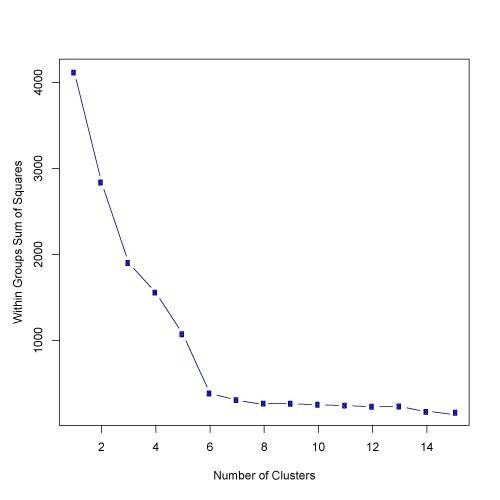

1. 5

2. 6

3. 14

4. 大于14

答案：B

根据上面的结果，使用 elbow 方法的簇数的最优选择是6。

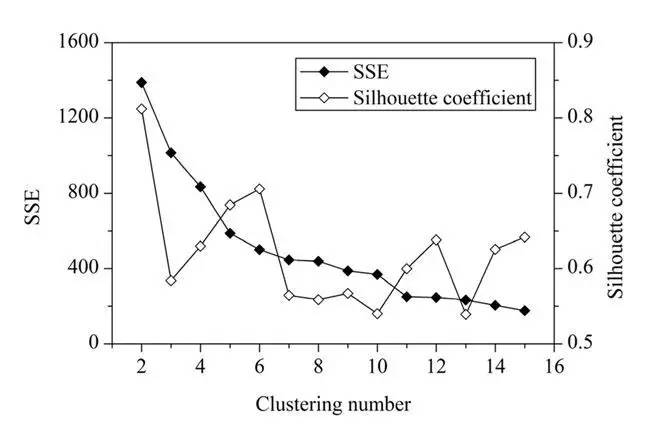
Q34. 根据下图的结果，簇的数量的最好选择是？**

1. 2

2. 4

3. 6

4. 8

答案：C

一般来说，平均轮廓系数越高，聚类的质量也相对较好。在这道题中，对于研究区域的网格单元，最优聚类数应该是2，这时平均轮廓系数的值最高。但是，聚类结果（k=2）的 SSE 值太大了。当 k=6 时，SEE 的值会低很多，但此时平均轮廓系数的值非常高，仅仅比 k=2 时的值低一点。因此，k=6 是最佳的选择。

Q35. 对于在初始化中使用了 Forgy 方法的K均值算法，下面哪个顺序是正确的？
**

1. 指定簇的数量

2. 随机分配簇的质心

3. 将每个数据点分配给最近的簇质心

4. 将每个点重新分配给最近的簇质心

5. 重新计算簇的质心

选项：

1. 1 2 3 5 4

2. 1 3 2 4 5

3. 2 1 3 4 5

4. 以上都不是

答案：A

用于K均值初始化的方法是 Forgy 和随机分区。Forgy 方法从数据集中随机选择k个观测值，并将其作为初始值。随机分区方法是先随机为每个观测值分配一个簇，随后进行更新，簇的随机分配点的质心就是计算后得到的初始平均值。

Q36. 如果你要用具有期望最大化算法的多项混合模型将一组数据点聚类到两个集群中，下面有哪些重要的假设？
**

1. 所有数据点遵循两个高斯分布

2. 所有数据点遵循n个高斯分布(n>2)

3. 所有数据点遵循两个多项分布

4. 所有数据点遵循n个多项分布(n>2)

答案：C

在聚类中使用期望最大化算法，本质是将数据点按照所选数量的簇进行分类，这个数量和预期生成的不同分布的数量是相同的，而且分布也必须是相同的类型。

Q37. 下面对基于质心的K均值聚类分析算法和基于分布的期望最大化聚类分析算法的描述，哪些是不正确的？
**

1. 都从随机初始化开始

2. 都是可迭代算法

3. 两者对数据点的假设很强

4. 都对异常值敏感

5. 期望最大化算法是K均值的特殊情况

6. 都需要对所需要的簇数有先验知识

7. 结果是不可再现的。

选项：

1. 1

2. 5

3. 1 3

4. 6 7

5. 4 6 7

6. 以上都不是

答案：B

上面的描述中只有第五个是错的，K均值是期望最大化算法的特殊情况，K均值是在每次迭代中只计算聚类分布的质心。

Q38. 下面关于 DBSCAN 聚类算法的描述不正确的是？
**

1. 集群中的数据点必须处于到核心点的距离阈限内

2. 它对数据空间中数据点的分布有很强的假设

3. 它具有相当高的时间复杂度O(n3)

4. 它不需要预先知道期望出现的簇的数量

5. 它对于异常值具有强大的作用

选项：

1. 1

2. 2

3. 4

4. 2 3

5. 1 5

6. 1 3 5

答案：D

DBSCAN 可以形成任意形状的聚类，数据点在数据空间的分布很难预测。
DBSCAN 有比较低的时间复杂度 O(n log n)。

Q39. 以下哪项的F分数存在上限和下限？
**

1. [0,1]

2. (0,1)

3. [-1,1]

4. 以上都不是

答案：A

F分数的最小可能值是0，最大可能值是1。1表示每个数据点都被分配给了正确的聚类，0表示聚类分析的旋进和（或）回调为0。在聚类分析中，我们期望出现的是F分数的高值。

Q40. 下面是对6000个数据点进行聚类分析后聚集成的3个簇：A、B和C：

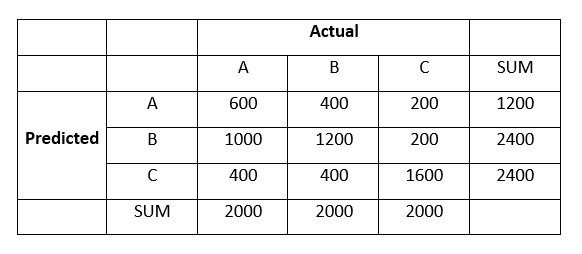
集群B的F1分数是多少？

1. 3

2. 4

3. 5

4. 6

答案：D

True Positive, TP = 1200
True Negative, TN = 600 + 1600 = 2200
False Positive, FP = 1000 + 200 = 1200
False Negative, FN = 400 + 400 = 800

因此，
Precision = TP / (TP + FP) = 0.5
Recall = TP / (TP + FN) = 0.6

最后，
F1 = 2 (Precision Recall)/(Precision + recall) = 0.54 ~ 0.5

结 语**

真心希望这次测试的答案对你有用。本次测试的重点主要集中在概念、聚类基本原理以及各种技术的实践知识等方面。

测试数据科学家聚类技术的40个问题（能力测验和答案）（上）

本文作者 Saurav Kaushik 是数据科学爱好者，还有一年他就从新德里 MAIT 毕业了，喜欢使用机器学习和分析来解决复杂的数据问题。

本文由 AI100 编译，转载需得到本公众号同意。

编译：AI100

原文链接：https://www.analyticsvidhya.com/blog/2017/02/test-data-scientist-clustering/

查看更多 AI 最新头条，请访问 AI100 微信公众号：

点击↙阅读原文↙查看更多资讯
阅读原文