kmeans聚类理论篇 - bourneli - 博客园 - 图1 分享到 kmeans聚类理论篇 - bourneli - 博客园 - 图2

QQ空间微博腾讯微博人人网微信一键分享查看更多(96)kmeans聚类理论篇 - bourneli - 博客园 - 图3JiaThis | | —- | —- |

kmeans聚类理论篇 - bourneli - 博客园 - 图4# bourneli(李伯韬)的技术博客

博客搬家了，新的日志会在一数一世界更新！

  • 博客园
  • 首页
  • 新随笔
  • 联系

  • 订阅

  • 管理 随笔 - 119 文章 - 17 评论 - 62# kmeans聚类理论篇
    前言
    kmeans是最简单的聚类算法之一，但是运用十分广泛。最近在工作中也经常遇到这个算法。kmeans一般在数据分析前期使用，选取适当的k，将数据分类后，然后分类研究不同聚类下数据的特点。
    本文记录学习kmeans算法相关的内容，包括算法原理，收敛性，效果评估聚，最后带上R语言的例子，作为备忘。

    算法原理
    kmeans的计算方法如下：
    1 随机选取k个中心点
    2 遍历所有数据，将每个数据划分到最近的中心点中
    3 计算每个聚类的平均值，并作为新的中心点
    4 重复2-3，直到这k个中线点不再变化（收敛了），或执行了足够多的迭代
    时间复杂度：O(Inkm)
    空间复杂度：O(n    m)
    其中m为每个元素字段个数，n为数据量，I为跌打个数。一般I,k,m均可认为是常量，所以时间和空间复杂度可以简化为O(n)，即线性的。

    算法收敛
    从kmeans的算法可以发现，SSE其实是一个严格的坐标下降（Coordinate Decendet）过程。设目标函数SSE如下：
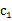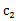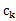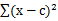
    SSE(kmeans聚类理论篇 - bourneli - 博客园 - 图5,kmeans聚类理论篇 - bourneli - 博客园 - 图6,…,kmeans聚类理论篇 - bourneli - 博客园 - 图7) = kmeans聚类理论篇 - bourneli - 博客园 - 图8
    采用欧式距离作为变量之间的聚类函数。每次朝一个变量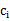kmeans聚类理论篇 - bourneli - 博客园 - 图9的方向找到最优解，也就是求偏倒数，然后等于0，可得
    c_i=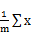kmeans聚类理论篇 - bourneli - 博客园 - 图10 其中m是c_i所在的簇的元素的个数
    也就是当前聚类的均值就是当前方向的最优解（最小值），这与kmeans的每一次迭代过程一样。所以，这样保证SSE每一次迭代时，都会减小，最终使SSE收敛。
    由于SSE是一个非凸函数（non-convex function），所以SSE不能保证找到全局最优解，只能确保局部最优解。但是可以重复执行几次kmeans，选取SSE最小的一次作为最终的聚类结果。

    0-1规格化
    由于数据之间量纲的不相同，不方便比较。举个例子，比如游戏用户的在线时长和活跃天数，前者单位是秒，数值一般都是几千，而后者单位是天，数值一般在个位或十位，如果用这两个变量来表征用户的活跃情况，显然活跃天数的作用基本上可以忽略。所以，需要将数据统一放到0~1的范围，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。具体计算方法如下：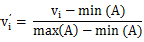
    kmeans聚类理论篇 - bourneli - 博客园 - 图11
    其中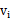kmeans聚类理论篇 - bourneli - 博客园 - 图12属于A。
    轮廓系数
    轮廓系数（Silhouette Coefficient）结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。具体计算方法如下：

  1. 对于第i个元素x_i，计算x_i与其同一个簇内的所有其他元素距离的平均值，记作a_i，用于量化簇内的凝聚度。
  2. 选取x_i外的一个簇b，计算x_i与b中所有点的平均距离，遍历所有其他簇，找到最近的这个平均距离,记作b_i，用于量化簇之间分离度。
  3. 对于元素x_i，轮廓系数s_i = (b_i – a_i)/max(a_i,b_i)
  4. 计算所有x的轮廓系数，求出平均值即为当前聚类的整体轮廓系数

从上面的公式，不难发现若s_i小于0，说明x_i与其簇内元素的平均距离小于最近的其他簇，表示聚类效果不好。如果a_i趋于0，或者b_i足够大，那么s_i趋近与1，说明聚类效果比较好。

K值选取
在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

实际应用
下面通过例子（R实现，完整代码见附件）讲解kmeans使用方法，会将上面提到的内容全部串起来 ?| | library(fpc)``# install.packages("fpc")``data(iris)``head(iris) | | —- | —- |

加载实验数据iris，这个数据在机器学习领域使用比较频繁，主要是通过画的几个部分的大小，对花的品种分类，实验中需要使用fpc库估计轮廓系数，如果没有可以通过install.packages安装。 ?| | # 0-1 正规化数据``min.max.norm <- ``function``(x){`` ``(x-min(x))/(max(x)-min(x))``}``raw.data <- iris[,1:4]``norm.data <- data.frame(sl = min.max.norm(raw.data[,1]),`` ``sw = min.max.norm(raw.data[,2]),`` ``pl = min.max.norm(raw.data[,3]),`` ``pw = min.max.norm(raw.data[,4])) | | —- | —- |

对iris的4个feature做数据正规化，每个feature均是花的某个不为的尺寸。 ?| | # k取2到8，评估K``K <- 2:8``round <- 30``# 每次迭代30次，避免局部最优``rst <- sapply(K, ``function``(i){`` ``print(paste(``"K="``,i))`` ``mean(sapply(1:round,``function``(r){`` ``print(paste(``"Round"``,r))`` ``result <- kmeans(norm.data, i)`` ``stats <- cluster.stats(dist(norm.data), result$cluster)`` ``stats$avg.silwidth`` ``}))``})``plot(K,rst,type=``'l'``,main=``'轮廓系数与K的关系'``, ylab=``'轮廓系数'``) | | —- | —- |

评估k，由于一般K不会太大，太大了也不易于理解，所以遍历K为2到8。由于kmeans具有一定随机性，并不是每次都收敛到全局最小，所以针对每一个k值，重复执行30次，取并计算轮廓系数，最终取平均作为最终评价标准，可以看到如下的示意图，

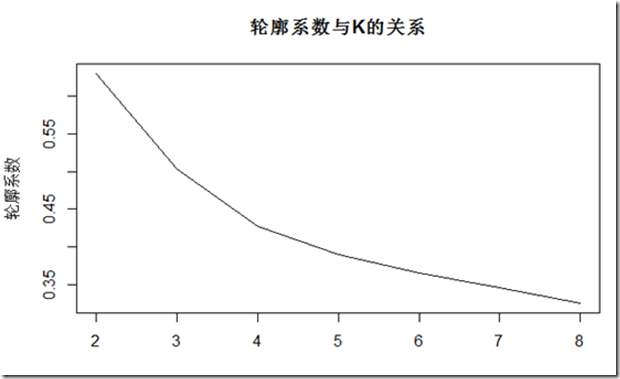
kmeans聚类理论篇 - bourneli - 博客园 - 图13

当k取2时，有最大的轮廓系数，虽然实际上有3个种类。 ?| | # 降纬度观察``old.par <- par(mfrow = c(1,2))``k = 2``# 根据上面的评估 k=2最优``clu <- kmeans(norm.data,k)``mds = cmdscale(dist(norm.data,method=``"euclidean"``))``plot(mds, col=clu$cluster, main=``'kmeans聚类 k=2'``, pch = 19)``plot(mds, col=iris$Species, main=``'原始聚类'``, pch = 19)``par(old.par) | | —- | —- |

聚类完成后，有源原始数据是4纬，无法可视化，所以通过多维定标(Multidimensional scaling)将纬度将至2为，查看聚类效果，如下

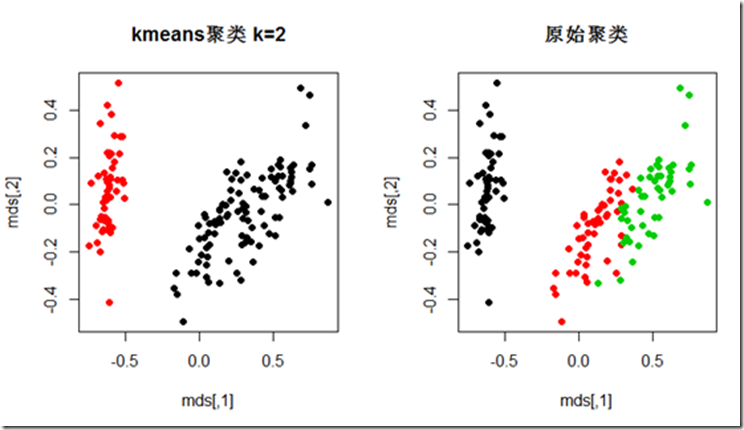
kmeans聚类理论篇 - bourneli - 博客园 - 图14
可以发现原始分类中和聚类中左边那一簇的效果还是拟合的很好的，右测原始数据就连在一起，kmeans无法很好的区分，需要寻求其他方法。

kmeans最佳实践
1. 随机选取训练数据中的k个点作为起始点
2. 当k值选定后，随机计算n次，取得到最小开销函数值的k作为最终聚类结果，避免随机引起的局部最优解
3. 手肘法选取k值：绘制出k—开销函数闪点图，看到有明显拐点（如下）的地方，设为k值，可以结合轮廓系数。
4. k值有时候需要根据应用场景选取，而不能完全的依据评估参数选取。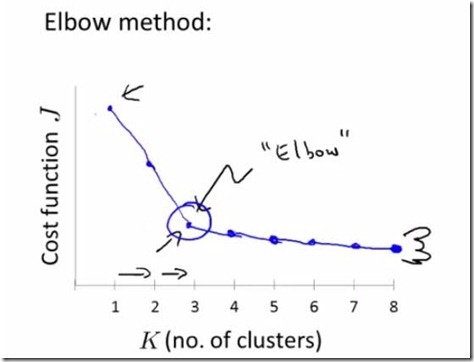
kmeans聚类理论篇 - bourneli - 博客园 - 图15


参考
[1] kmeans 讲义by Andrew NG
[2] 坐标下降法（Coordinate Decendent）
[3] 数据规格化
[4] 维基百科—轮廓系数)
[5] kmeans算法介绍
[6] 降为方法—多维定标
[7] Week 8 in Machine Learning, by Andrew NG, Coursera 数据分析&挖掘R好文要顶关注我收藏该文kmeans聚类理论篇 - bourneli - 博客园 - 图16kmeans聚类理论篇 - bourneli - 博客园 - 图17kmeans聚类理论篇 - bourneli - 博客园 - 图18bourneli
关注 - 9
粉丝 - 143+加关注30« PCA主成份分析学习记要
» R绘制3D散点图
2014-04-04 13:59bourneli498534编辑收藏
#1楼2015-09-24 19:58fanfan123 支持(0)反对(0)#2楼2016-05-23 14:04stillwatersi 支持(0)反对(0)#3楼2017-07-27 16:46DC_lambert 支持(0)反对(0)#4楼2017-07-27 16:47wendy0 支持(0)反对(0)刷新评论刷新页面返回顶部登录注册访问【推荐】50万行VC++源码: 大型组态工控、电力仿真CAD与GIS源码库
【活动】阿里云双11活动开始预热 云服务器限时2折起
【调查】有奖调研即刻参与，你竟然是酱紫程序猿！
【推荐】Vue.js 2.x 快速入门，大量高效实战示例
kmeans聚类理论篇 - bourneli - 博客园 - 图19
腾讯股价频创历史新高 马化腾重登中国首富宝座
乐视致新发公开信：让商业回归本质 业务不受外部影响
Skype视频面试服务更新加入群面和更多编程语言
逾8成企业雇员认为Face ID可靠，能取代密码
京东商城“跨界”住房租赁电商业务：正在收购域名
更多新闻…kmeans聚类理论篇 - bourneli - 博客园 - 图20
改善程序员生活质量的 3+10 习惯
NASA的10条代码编写原则
为什么你参加了那么多培训，却依然表现平平？
写给初学前端工程师的一封信
实用VPC虚拟私有云设计原则
更多知识库文章…### 公告 bourneli
5年11个月
143
9+加关注| | < | 2017年11月 | > | | —- | —- | —- |
日 一 二 三 四 五 六
29 30 31 1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 1 2
3 4 5 6 7 8 9

搜索

最新随笔

最新评论