pca 和lda区别
2017年1月26日 星期四
23:49
http://blog.csdn.net/scyscyao/article/details/5987581
这学期选了门模式识别的课。发现最常见的一种情况就是,书上写的老师ppt上写的都看不懂,然后绕了一大圈去自己查资料理解,回头看看发现,Ah-ha,原来本质的原理那么简单,自己一开始只不过被那些看似formidable的细节吓到了。所以在这里把自己所学的一些点记录下来,供备忘,也供参考。
1. K-Nearest Neighbor
K-NN可以说是一种最直接的用来分类未知数据的方法。基本通过下面这张图跟文字说明就可以明白K-NN是干什么的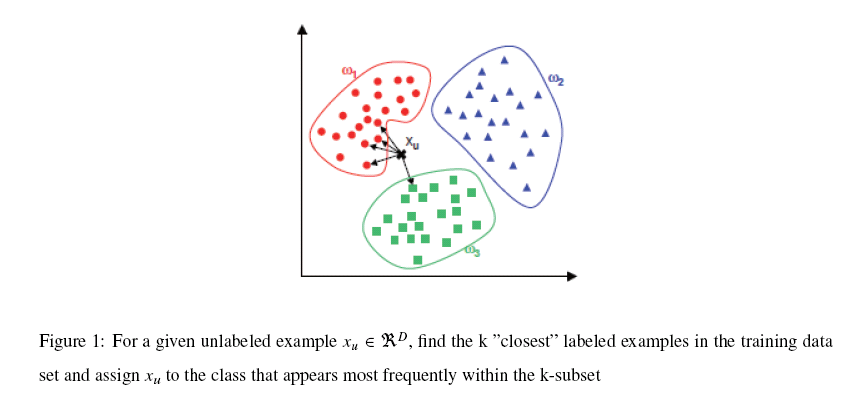
简单来说,K-NN可以看成:有那么一堆你已经知道分类的数据,然后当一个新数据进入的时候,就开始跟训练数据里的每个点求距离,然后挑离这个训练数据最近的K个点看看这几个点属于什么类型,然后用少数服从多数的原则,给新数据归类。一个比较好的介绍k-NN的课件可以见下面链接,图文并茂,我当时一看就懂了
http://courses.cs.tamu.edu/rgutier/cs790_w02/l8.pdf
实际上K-NN本身的运算量是相当大的,因为数据的维数往往不止2维,而且训练数据库越大,所求的样本间距离就越多。就拿我们course project的人脸检测来说,输入向量的维数是1024维(32x32的图,当然我觉得这种方法比较silly),训练数据有上千个,所以每次求距离(这里用的是欧式距离,就是我们最常用的平方和开根号求距法) 这样每个点的归类都要花上上百万次的计算。所以现在比较常用的一种方法就是kd-tree。也就是把整个输入空间划分成很多很多小子区域,然后根据临近的原则把它们组织为树形结构。然后搜索最近K个点的时候就不用全盘比较而只要比较临近几个子区域的训练数据就行了。kd-tree的一个比较好的课件可以见下面链接:
http://www.inf.ed.ac.uk/teaching/courses/inf2b/learnnotes/inf2b-learn06-lec.pdf
当然,kd-tree有一个问题就是当输入维数跟训练数据数量很接近时就很难优化了。所以用PCA(稍后会介绍)降维大多数情况下是很有必要的
2. Bayes Classifier
贝叶斯方法一篇比较科普的中文介绍可以见pongba的平凡而神奇的贝叶斯方法: http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/,实际实现一个贝叶斯分类器之后再回头看这篇文章,感觉就很不一样。
在模式识别的实际应用中,贝叶斯方法绝非就是post正比于priorlikelihood这个公式这么简单,一般而言我们都会用正态分布拟合likelihood来实现。
用正态分布拟合是什么意思呢?贝叶斯方法式子的右边有两个量,一个是prior先验概率,这个求起来很简单,就是一大堆数据中求某一类数据占的百分比就可以了,比如300个一堆的数据中A类数据占100个,那么A的先验概率就是1/3。第二个就是likelihood,likelihood可以这么理解:对于每一类的训练数据,我们都用一个multivariate正态分布来拟合它们(即通过求得某一分类训练数据的平均值和协方差矩阵来拟合出一个正态分布),然后当进入一个新的测试数据之后,就分别求取这个数据点在每个类别的正态分布中的大小,然后用这个值乘以原先的prior便是所要求得的后验概率post了。
贝叶斯公式中还有一个evidence,对于初学者来说,可能会一下没法理解为什么在实际运算中它不见了。实则上,evidence只是一个让最后post归一化的东西,而在模式分类中,我们只需要比较不同类别间post的大小,归一化反而增加了它的运算量。当然,在有的地方,这个evidence绝对不能省,比如后文提到的GMM中,需要用到EM迭代,这时候如果不用evidence将post归一化,后果就会很可怕。
Bayes方法一个不错的参考网页可见下面链接:
http://www.cs.mcgill.ca/~mcleish/644/main.html
3. Principle Component Analysis
PCA,译为主元分析或者主成份分析,是一种很好的简化数据的方法,也是PR中常见到不能再常见的算法之一。CSDN上有一篇很不错的中文博客介绍PCA,《主元分析(PCA)理论分析及应用》,可以见下面链接:
http://blog.csdn.net/ayw_hehe/archive/2010/07/16/5736659.aspx
对于我而言,主元分析最大的意义就是让我明白了线性代数中特征值跟特征向量究竟代表什么,从而让我进一步感受到了线性代数的博大精深魅力无穷。- -|||
PCA简而言之就是根据输入数据的分布给输入数据重新找到更能描述这组数据的正交的坐标轴,比如下面一幅图,对于那个椭圆状的分布,最方便表示这个分布的坐标轴肯定是椭圆的长轴短轴而不是原来的x y。
那么如何求出这个长轴和短轴呢?于是线性代数就来了:我们求出这堆数据的协方差矩阵(关于什么是协方差矩阵,详见本节最后附的链接),然后再求出这个协方差矩阵的特征值和特征向量,对应最大特征值的那个特征向量的方向就是长轴(也就是主元)的方向,次大特征值的就是第二主元的方向,以此类推。
关于PCA,推荐两个不错的tutorial:
(1) A tutorial on Principle Component Analysis从最基本的数学原理到应用都有,让我在被老师的讲课弄晕之后瞬间开悟的tutorial:
http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
(2) 里面有一个很生动的实现PCA的例子,还有告诉你PCA跟SVD是什么关系的,对编程实现的帮助很大(当然大多数情况下都不用自己编了):
http://www.math.ucsd.edu/~gptesler/283/pca_07-handout.pdf
4. Linear Discriminant Analysis
LDA,基本和PCA是一对双生子,它们之间的区别就是PCA是一种unsupervised的映射方法而LDA是一种supervised映射方法,这一点可以从下图中一个2D的例子简单看出
图的左边是PCA,它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据内部的分类信息。因此,虽然做了PCA后,整组数据在表示上更加方便(降低了维数并将信息损失降到最低),但在分类上也许会变得更加困难;图的右边是LDA,可以明显看出,在增加了分类信息之后,两组输入映射到了另外一个坐标轴上,有了这样一个映射,两组数据之间的就变得更易区分了(在低维上就可以区分,减少了很大的运算量)。
PCA 是无监督的,它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据内部的分类信息
用主要的特征代替其他相关的非主要的特征,所有特征之间的相关度越高越好
但是分类任务的特征可能是相互独立的
LDA是有监督的,使得类别内的点距离越近越好(集中),类别间的点越远越好。
在实际应用中,最常用的一种LDA方法叫作Fisher Linear Discriminant,其简要原理就是求取一个线性变换,是的样本数据中“between classes scatter matrix”(不同类数据间的协方差矩阵)和“within classes scatter matrix”(同一类数据内部的各个数据间协方差矩阵)之比的达到最大。关于Fisher LDA更具体的内容可以见下面课件,写的很不错~
http://www.csd.uwo.ca/~olga/Courses//CS434a_541a//Lecture8.pdf
5. Non-negative Matrix Factorization
NMF,中文译为非负矩阵分解。一篇比较不错的NMF中文介绍文可以见下面一篇博文的链接,《非负矩阵分解:数学的奇妙力量》
http://chnfyn.blog.163.com/blog/static/26954632200751625243295/
这篇博文很大概地介绍了一下NMF的来龙去脉(当然里面那幅图是错的。。。),当然如果你想更深入地了解NMF的话,可以参考Lee和Seung当年发表在Nature上面的NMF原文,”Learning the parts of objects by non-negative matrix factorization”
http://www.seas.upenn.edu/~ddlee/Papers/nmf.pdf
读了这篇论文,基本其他任何介绍NMF基本方法的材料都是浮云了。
NMF,简而言之,就是给定一个非负矩阵V,我们寻找另外两个非负矩阵W和H来分解它,使得后W和H的乘积是V。论文中所提到的最简单的方法,就是根据最小化||V-WH||的要求,通过Gradient Discent推导出一个update rule,然后再对其中的每个元素进行迭代,最后得到最小值,具体的update rule见下图,注意其中Wia等带下标的符号表示的是矩阵里的元素,而非代表整个矩阵,当年在这个上面绕了好久。。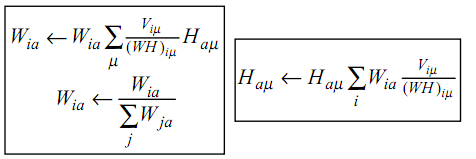
当然上面所提的方法只是其中一种而已,在http://spinner.cofc.edu/~langvillea/NISS-NMF.pdf中有更多详细方法的介绍。
相比于PCA、LDA,NMF有个明显的好处就是它的非负,因为为在很多情况下带有负号的运算算起来都不这么方便,但是它也有一个问题就是NMF分解出来的结果不像PCA和LDA一样是恒定的。
6. Gaussian Mixture Model
GMM高斯混合模型粗看上去跟上文所提的贝叶斯分类器有点类似,但两者的方法有很大的不同。在贝叶斯分类器中,我们已经事先知道了训练数据(training set)的分类信息,因此只要根据对应的均值和协方差矩阵拟合一个高斯分布即可。而在GMM中,我们除了数据的信息,对数据的分类一无所知,因此,在运算时我们不仅需要估算每个数据的分类,还要估算这些估算后数据分类的均值和协方差矩阵。。。也就是说如果有1000个训练数据10租分类的话,需要求的未知数是1000+10+10(用未知数表示未必确切,确切的说是1000个1x10标志向量,10个与训练数据同维的平均向量,10个与训练数据同维的方阵)。。。反正想想都是很头大的事情。。。那么这个问题是怎么解决的呢?
这里用的是一种叫EM迭代的方法。
具体使用方法可以参考http://neural.cs.nthu.edu.tw/jang/books/dcpr/doc/08gmm.pdf 这份台湾清华大学的课件,写的真是相当的赞,实现代码的话可以参考:
1. 倩倩的博客http://www.cnblogs.com/jill_new/archive/2010/12/01/1893851.html 和
2. http://www.cs.ru.nl/~ali/EM.m
当然 Matlab里一般也会自带GMM工具箱,其用法可以参考下面链接:
http://www.mathworks.com/help/toolbox/stats/gmdistribution.fit.html
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
LDA:
LDA的全称是Linear Discriminant Analysis(线性判别分析),是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant,因为它被Ronald Fisher发明自1936年,Discriminant这次词我个人的理解是,一个模型,不需要去通过概率的方法来训练、预测数据,比如说各种贝叶斯方法,就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法,据我所知,百度的商务搜索部里面就用了不少这方面的算法。
LDA的原理是,将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近。要说明白LDA,首先得弄明白线性分类器(Linear Classifier):因为LDA是一种线性分类器。对于K-分类的一个分类问题,会有K个线性函数:
当满足条件:对于所有的j,都有Yk > Yj,的时候,我们就说x属于类别k。对于每一个分类,都有一个公式去算一个分值,在所有的公式得到的分值中,找一个最大的,就是所属的分类了。
上式实际上就是一种投影,是将一个高维的点投影到一条高维的直线上,LDA最求的目标是,给出一个标注了类别的数据集,投影到了一条直线之后,能够使得点尽量的按类别区分开,当k=2即二分类问题的时候,如下图所示: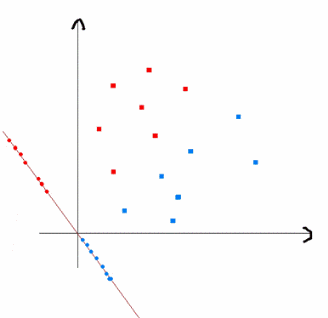
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点,经过原点的那条线就是投影的直线,从图上可以清楚的看到,红色的点和蓝色的点被原点明显的分开了,这个数据只是随便画的,如果在高维的情况下,看起来会更好一点。下面我来推导一下二分类LDA问题的公式:
假设用来区分二分类的直线(投影函数)为:
LDA分类的一个目标是使得不同类别之间的距离越远越好,同一类别之中的距离越近越好,所以我们需要定义几个关键的值。
类别i的原始中心点为:(Di表示属于类别i的点)
类别i投影后的中心点为:
衡量类别i投影后,类别点之间的分散程度(方差)为:
最终我们可以得到一个下面的公式,表示LDA投影到w后的损失函数:
我们分类的目标是,使得类别内的点距离越近越好(集中),类别间的点越远越好。分母表示每一个类别内的方差之和,方差越大表示一个类别内的点越分散,分子为两个类别各自的中心点的距离的平方,我们最大化J(w)就可以求出最优的w了。想要求出最优的w,可以使用拉格朗日乘子法,但是现在我们得到的J(w)里面,w是不能被单独提出来的,我们就得想办法将w单独提出来。
我们定义一个投影前的各类别分散程度的矩阵,这个矩阵看起来有一点麻烦,其实意思是,如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近,则Si里面元素的值就越小,如果分类的点都紧紧地围绕着mi,则Si里面的元素值越更接近0.
带入Si,将J(w)分母化为: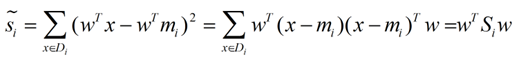
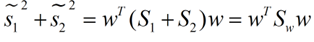
同样的将J(w)分子化为:
这样损失函数可以化成下面的形式:
这样就可以用最喜欢的拉格朗日乘子法了,但是还有一个问题,如果分子、分母是都可以取任意值的,那就会使得有无穷解,我们将分母限制为长度为1(这是用拉格朗日乘子法一个很重要的技巧,在下面将说的PCA里面也会用到,如果忘记了,请复习一下高数),并作为拉格朗日乘子法的限制条件,带入得到: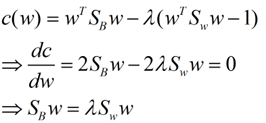
这样的式子就是一个求特征值的问题了。
对于N(N>2)分类的问题,我就直接写出下面的结论了: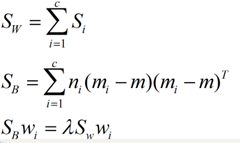
这同样是一个求特征值的问题,我们求出的第i大的特征向量,就是对应的Wi了。
这里想多谈谈特征值,特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用,特征值表示的是矩阵的性质,当我们取到矩阵的前N个最大的特征值的时候,我们可以说提取到的矩阵主要的成分(这个和之后的PCA相关,但是不是完全一样的概念)。在机器学习领域,不少的地方都要用到特征值的计算,比如说图像识别、pagerank、LDA、还有之后将会提到的PCA等等。
下图是图像识别中广泛用到的特征脸(eigen face),提取出特征脸有两个目的,首先是为了压缩数据,对于一张图片,只需要保存其最重要的部分就是了,然后是为了使得程序更容易处理,在提取主要特征的时候,很多的噪声都被过滤掉了。跟下面将谈到的PCA的作用非常相关。
特征值的求法有很多,求一个D D的矩阵的时间复杂度是O(D^3), 也有一些求Top M的方法,比如说power method,它的时间复杂度是O(D^2 * M), 总体来说,求特征值是一个很费时间的操作,如果是单机环境下,是很局限的。
PCA:
主成分分析(PCA)与LDA有着非常近似的意思,LDA的输入数据是带标签的,而PCA的输入数据是不带标签的,所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在,给定了训练数据后,将会得到一系列的判别函数(discriminate function),之后对于新的输入,就可以进行预测了。而PCA更像是一个预处理的方法,它可以将原本的数据降低维度,而使得降低了维度的数据之间的方差最大(也可以说投影误差最小,具体在之后的推导里面会谈到)。
方差这个东西是个很有趣的,有些时候我们会考虑减少方差(比如说训练模型的时候,我们会考虑到方差-偏差的均衡),有的时候我们会尽量的增大方差。方差就像是一种信仰(强哥的话),不一定会有很严密的证明,从实践来说,通过尽量增大投影方差的PCA算法,确实可以提高我们的算法质量。
说了这么多,推推公式可以帮助我们理解。我下面将用两种思路来推导出一个同样的表达式。首先是最大化投影后的方差,其次是最小化投影后的损失(投影产生的损失最小)。
最大化方差法:
假设我们还是将一个空间中的点投影到一个向量中去。首先,给出原空间的中心点:
假设u1为投影向量,投影之后的方差为:
上面这个式子如果看懂了之前推导LDA的过程,应该比较容易理解,如果线性代数里面的内容忘记了,可以再温习一下,优化上式等号右边的内容,还是用拉格朗日乘子法:
将上式求导,使之为0,得到:
这是一个标准的特征值表达式了,λ对应的特征值,u对应的特征向量。上式的左边取得最大值的条件就是λ1最大,也就是取得最大的特征值的时候。假设我们是要将一个D维的数据空间投影到M维的数据空间中(M < D), 那我们取前M个特征向量构成的投影矩阵就是能够使得方差最大的矩阵了。
最小化损失法:
假设输入数据x是在D维空间中的点,那么,我们可以用D个正交的D维向量去完全的表示这个空间(这个空间中所有的向量都可以用这D个向量的线性组合得到)。在D维空间中,有无穷多种可能找这D个正交的D维向量,哪个组合是最合适的呢?
假设我们已经找到了这D个向量,可以得到:
我们可以用近似法来表示投影后的点:
上式表示,得到的新的x是由前M 个基的线性组合加上后D - M个基的线性组合,注意这里的z是对于每个x都不同的,而b对于每个x是相同的,这样我们就可以用M个数来表示空间中的一个点,也就是使得数据降维了。但是这样降维后的数据,必然会产生一些扭曲,我们用J描述这种扭曲,我们的目标是,使得J最小:
上式的意思很直观,就是对于每一个点,将降维后的点与原始的点之间的距离的平方和加起来,求平均值,我们就要使得这个平均值最小。我们令:
将上面得到的z与b带入降维的表达式:
将上式带入J的表达式得到:
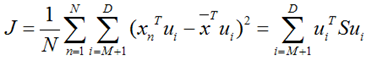
再用上拉普拉斯乘子法(此处略),可以得到,取得我们想要的投影基的表达式为:
这里又是一个特征值的表达式,我们想要的前M个向量其实就是这里最大的M个特征值所对应的特征向量。证明这个还可以看看,我们J可以化为:
也就是当误差J是由最小的D - M个特征值组成的时候,J取得最小值。跟上面的意思相同。
下图是PCA的投影的一个表示,黑色的点是原始的点,带箭头的虚线是投影的向量,Pc1表示特征值最大的特征向量,pc2表示特征值次大的特征向量,两者是彼此正交的,因为这原本是一个2维的空间,所以最多有两个投影的向量,如果空间维度更高,则投影的向量会更多。
总结:
本次主要讲了两种方法,PCA与LDA,两者的思想和计算方法非常类似,但是一个是作为独立的算法存在,另一个更多的用于数据的预处理的工作。另外对于PCA和LDA还有核方法,本次的篇幅比较大了,先不说了,以后有时间再谈:
已使用 Microsoft OneNote 2016 创建。

