从某种程度上说, 我们的世界是由最优化问题组成的
每一天,我们的生活都面临无数的最优化问题: 上班怎么选择乘车路线,才能舒服又快速的到达公司;旅游如何选择航班和宾馆,既省钱又能玩的开心; 跳槽应该选择哪家公司,钱多、事少、离家近,前台妹子颜值高;买房子应该选在哪里,交通发达有学区,生活便利升值快。
可以看出,上面所有的问题都面临无数的选择, 我们会根据自己的偏好对每个选择打一个不同的分数,再从所有的选择中找出最优的一个。这个寻求最优解的过程其实就是最优化问题,我们要打的分数就称为目标函数。
最优化问题往往还要面临一定的约束条件,比如对旅行路线的选择,总花费和出发、到达时间就构成了约束条件,对买房子的选择,离公司的路程、总价也可能构成约束条件。我们选择的最优解也必须满足这些约束条件。
实际上,最优化问题是机器学习、人工智能等问题的基础,也在互联网广告、推荐系统、机器人、无人驾驶等领域有着广泛应用。
之前的文章里也有提到,目前炙手可热的深度学习的兴起也依赖于最优化方法的改进。最优化方法是机器学习中模型训练的基础,机器学习的很大一部分内容就是通过最优化方法找到最合适的参数,使得模型的目标函数最优。
最优化问题 - 定义
结合上面的例子,最优化问题就可以定义为: 在给定的约束条件下, 选择最优的参数和方案,来使得目标函数最大化 / 最小化的问题。
最优化问题的主要形式是:

这里可以引出最优化问题的三个基本要素:
- 目标函数: 用来衡量结果的好坏
- 参数值:未知的因子,需要通过数据来确定。
- 约束条件:需要满足的限制条件
最优化问题 - 举例
一个最简单的最优化问题,就是下面这个例子:

作为一个经典的最优化问题,三个基本要素分别为:
- 目标函数:最大化操场面积 S, S = x * y
- 参数值: 长 x、宽 y
- 约束条件: x + 2y = 60
如果大家高中碰到过类似问题的话,应该记得当初的主要思路是
- 把 y 表示成 x 的格式:面积 S = x*(60-x)/2
- 最大化 S,相当于对 x 求导,求导数等于 0 的点
- 得到 x= 30 , y = (60-x)/2 = 15, 最大的面积是 450
我们为什么能够这样求解?有几点原因:
- 目标函数连续并且可导
- 目标函数的一阶导数可以直接求解
- 问题是个凸优化问题,有且仅有 1 个全局最优点
- 只有两个变量
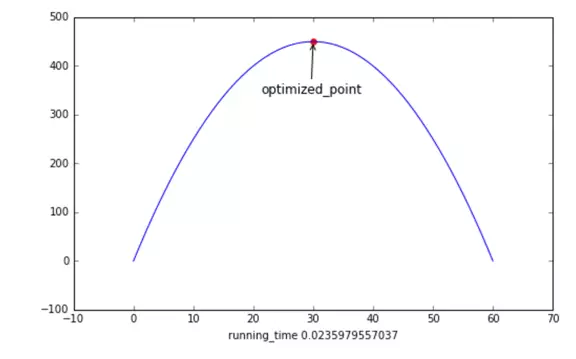
所以,上面的例子是个比较简单的最优化问题。如果上面的任何一个条件不满足的话,都不能用当前的方法求解,而需要求助于更复杂的方法。
比如, 目标函数不是凸函数时,可能有多个导数为 0 的点:
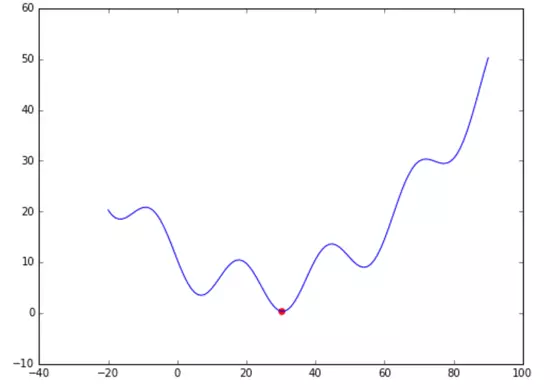
又比如,有可能有超过两个变量,那么优化问题就需要同时考虑多个参数,优化问题需要扩展到多维:
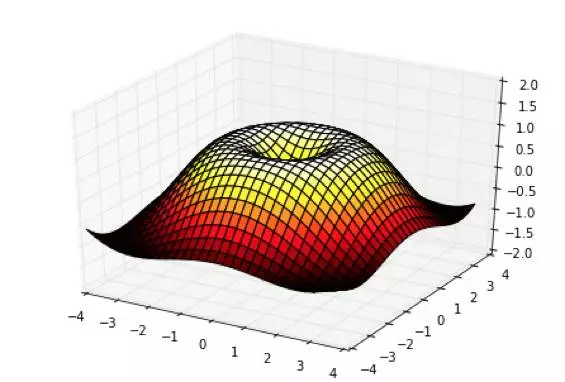
下面,我们就来介绍一下针对最优化问题的分类,以及对应的不同解法。
最优化问题 - 分类
根据约束条件的种类,最优化问题可以分成以下种类:
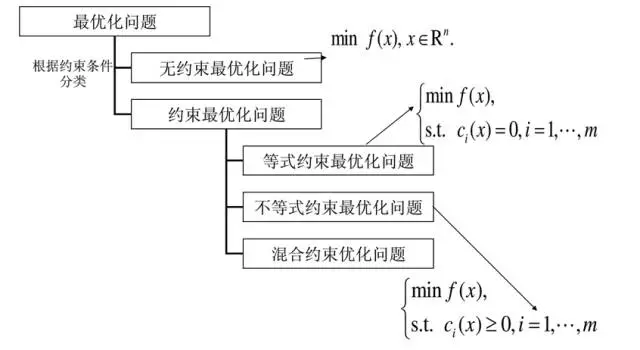
而根据目标函数的状态, 最优化问题又可以分成:
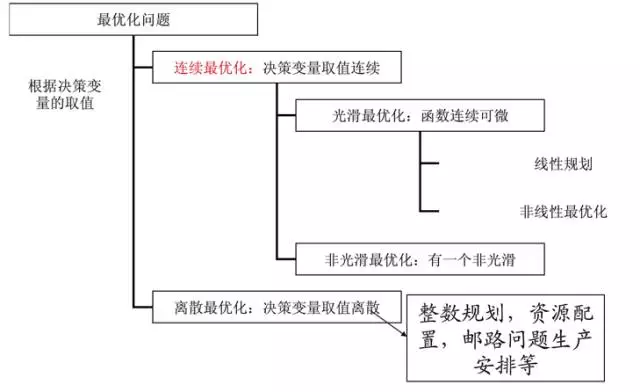
最优化问题 - 解法分类和选择
在实际的工作中,我们如何来选择最优化问题的解法呢?
基本的依据有以下几点:
- 目标函数是否连续可导
- 目标函数的形式,是否为线性函数或者二次函数
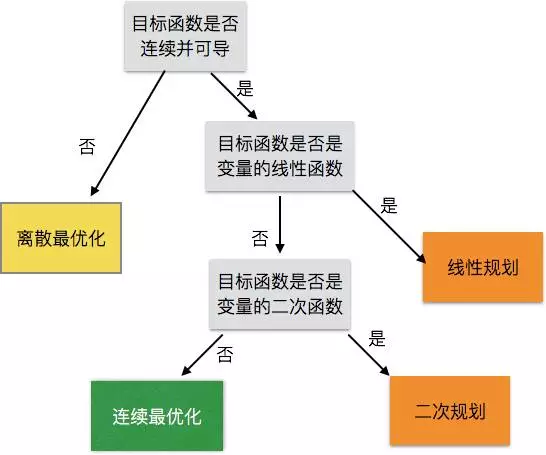
对应上图:
- 离散最优化方法: 主要用于求解目标函数不连续或者不可导的情况,典型的解法有爬山法、模拟退火、遗传算法和蚁群算法等。
- 线性规划和二次规划:运筹学的重要研究内容,适用于目标函数是线性或二次函数的形式。
- 连续最优化方法: 适用于逻辑回归、SVM、神经网络等机器学习问题,主要方法包括梯度下降、牛顿法和拟牛顿法。
更多精彩,敬请期待:


