判别分析与聚类分析

判别分析与聚类分析

原创2016-06-27吴利伟医研云

分类是面对生物学和医学数据时，从中提取有意义信息的基本手段，是非常重要的研究方法。 分类有两个要素：分类对象、分类依据 分类对象：有被分类的个体组成 分类依据：取决于被分类的个体所具有的性质 分类的统计学方法主要有两类：判别分析和聚类分析

判别分析
判别分析（discriminant analysis）：是在分类对象的类别归属明确的情况下，根据对象的某些特征构造判别函数来判定其类别归属的统计学方法。医学诊断的推理过程，可用数学方法精确描述。

经典判别方法：Fisher判别和Bayes判别。
Fisher判别：又称典则判别（canonical discriminant），适用于两类和多类判别。基本原理就是找到一个投影轴，使两类样本在投影轴上交叠部分最少，从而使分类效果达到最佳。这个投影轴就是判别函数。

判别规则：建立判别式后，逐例计算判别值，进一步求出两类判别值与总均属，然后进行判别。

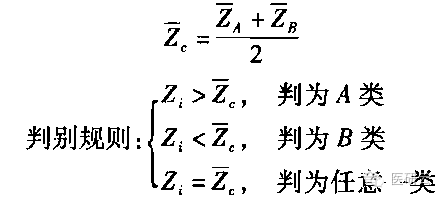
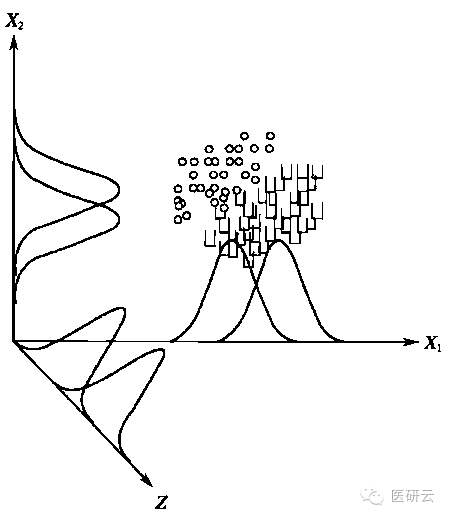
判别效果的评价
判别效果一般用误判概率P来衡量。误判概率可通过前瞻性和回顾性两种方式获得估计。回顾性误判概率估计是指用建立判别函数的样本回代判别，常会夸大判别效果。
一般，建立判别函数需要将随机样本分为两个部分，分别占总样本量的85%和15%，前者用于建立判别函数，成为训练样本。后者考核函数的判别效果，成为验证样本。
用验证样本计算的误判概率作为前瞻性误判概率估计比较客观。

刀切法（jackknife）误判概率估计：也称交叉核实法（cross validation）。步骤是：
1 顺序剔除一个样品，用余下的样品建立判别函数
2 用判别函数判别被剔除的样品
3 不断重复上两步，到全部判别完成
4 计算判别概率
样本量偏少时，本法比较客观。

多类判别：
多类中体的Fisher判别思路是先找到r个投影方向，使得每一个方向上类间变异尽量大，类内变异尽量小，且各方向两两不相关，然后用这r个判别函数构造判别规则，最后，给予r个判别函数，计算待判定的样品与各样本指标变量均数的距离，距离最小的就是这一类。

最大似然判别法
最大似然判别法又称尤度法，适用于指标为定性资料的两类判别或多类判别。此方法的基本思想是：当从模型总体随机抽取n组样本观测值后，最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大，而不是像最小二乘估计法旨在得到使得模型能最好地拟合样本数据的参数估计量。

Bayes公式判别法
与最大似然判别法原理相似，也是采用概率进行判别，要求各类近似服从多元正态分布，多用于多类判别。

最大似然判别法和Bayes公式判别法都是以概率为叛据，因此要求训练样本较大。

聚类分析
已知类别的归类叫判别分析。未知类别，找出分类，叫聚类分析。
聚类分析按照分类目的分为两大类：
1 R型聚类：又称指标聚类，是指将m个指标归类的方法，目的是指标降维从而选择有代表性的指标。
2 Q型聚类：又称样品聚类，是指将n个样品归类的方法，其目的是找出样品间的共性。

聚类关键问题是如何定义相似性，即如何把相似性数量化。相似性的指标度量即相似性系数（similarity coefficient）。

系统聚类（hierarchical clustering analysis）：是将相似的样品或变量归类的最常用的方法，过程如下：
1 将每个样品独自视为一类，计算类间的相似性系数矩阵。
2 将相似性系数最大（距离最小或相关系数最大）两类合并成新类
3 重复上述过程，直到全部合并成一类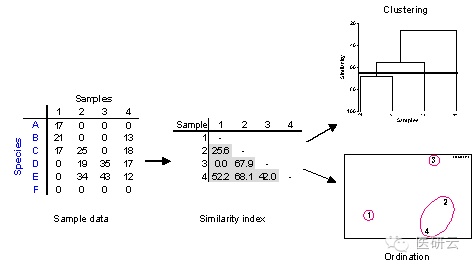

聚类分析现代应用越来越多，尤其是在数据挖掘过程中，我们用聚类分析能够快速给予数据个体大概分类，并提示一些内部结构和规律。现在，模糊数学、神经网络、支持矢量机等算法都已经用于判别分析和聚类分析，广泛用于人工智能和大数据处理。

阅读原文