Zset数据结构分析

命令查看

127.0.0.1:6379> zadd zset1 2 lisi
(integer) 1
127.0.0.1:6379> zadd zset1 1 zhangsan
(integer) 1
127.0.0.1:6379> zadd zset1 3 wangwu
(integer) 1
127.0.0.1:6379> zrange zset1 0 -1
1) "zhangsan"
2) "lisi"
3) "wangwu"
127.0.0.1:6379> object encoding zset1
"ziplist"
127.0.0.1:6379> zadd zset1 9999999999999 sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss
(integer) 1
127.0.0.1:6379> object encoding zset1
"skiplist"

我们可以看到zset的底层结构也是有两种， ziplist 和 skiplist 。

• zipList：满足以下两个条件
  • [score,value]键值对数量少于128个；
  • 每个元素的长度小于64字节；
• skipList：不满足以上两个条件时使用hash和skipList
  • hash用来存储value到score的映射，这样就可以在O(1)时间内找到value对应的分数；
  • skipList按照从小到大的顺序存储分数
  • skipList每个元素的值都是[socre,value]对。

简单来讲，dict用来查询数据到分数的对应关系，而skiplist用来根据分数查询数据（可能是范围查找）。

zipList和上一篇Set数据结构分析一样，这一篇主要说skipList。

skiplist是什么？

skiplist本质上也是一种查找结构，用于解决算法中的查找问题（Searching），即根据给定的key，快速查到它所在的位置（或者对应的value）。
我们在《Redis内部数据结构详解》系列的第一篇中介绍dict的时候，曾经讨论过：一般查找问题的解法分为两个大类：一个是基于各种平衡树，一个是基于哈希表。但skiplist却比较特殊，它没法归属到这两大类里面。
这种数据结构是由William Pugh发明的，最早出现于他在1990年发表的论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》。对细节感兴趣的同学可以下载论文原文来阅读。
skiplist，顾名思义，首先它是一个list。实际上，它是在有序链表的基础上发展起来的。

步骤一 新建一个有序链表

一个有序链表，如下图（最左侧的灰色节点表示一个空的头结点）：

在这样一个链表中，如果我们要查找某个数据，那么需要从头开始逐个进行比较，直到找到包含数据的那个节点，或者找到第一个比给定数据大的节点为止（没找到）。也就是说，时间复杂度为O(n)。同样，当我们要插入新数据的时候，也要经历同样的查找过程，从而确定插入位置。

步骤二 抽取二级索引节点

假如我们每相邻两个节点增加一个指针，让指针指向下下个节点，如下图：

这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半（上图中是7, 19, 26）。现在当我们想查找数据的时候，可以先沿着这个新链表进行查找。当碰到比待查数据大的节点时，再回到原来的链表中进行查找。比如，我们想查找23，查找的路径是沿着下图中标红的指针所指向的方向进行的：

• 23首先和7比较，再和19比较，比它们都大，继续向后比较。
• 但23和26比较的时候，比26要小，因此回到下面的链表（原链表），与22比较。
• 23比22要大，沿下面的指针继续向后和26比较。23比26小，说明待查数据23在原链表中不存在，而且它的插入位置应该在22和26之间。

在这个查找过程中，由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了。需要比较的节点数大概只有原来的一半。

步骤三 抽取三级索引节点

利用同样的方式，我们可以在上层新产生的链表上，继续为每相邻的两个节点增加一个指针，从而产生第三层链表。如下图：

在这个新的三层链表结构上，如果我们还是查找23，那么沿着最上层链表首先要比较的是19，发现23比19大，接下来我们就知道只需要到19的后面去继续查找，从而一下子跳过了19前面的所有节点。可以想象，当链表足够长的时候，这种多层链表的查找方式能让我们跳过很多下层节点，大大加快查找的速度。
skiplist正是受这种多层链表的想法的启发而设计出来的。实际上，按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似于一个二分查找，使得查找的时间复杂度可以降低到O(log n)。但是，这种方法在插入数据的时候有很大的问题。新插入一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。删除数据也有同样的问题。
skiplist为了避免这一问题，它不要求上下相邻两层链表之间的节点个数有严格的对应关系，而是为每个节点随机出一个层数(level)。比如，一个节点随机出的层数是3，那么就把它链入到第1层到第3层这三层链表中。

为了表达清楚，下图展示了如何通过一步步的插入操作从而形成一个skiplist的过程：

从上面skiplist的创建和插入过程可以看出，每一个节点的层数（level）是随机出来的，而且新插入一个节点不会影响其它节点的层数。因此，插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整。这就降低了插入操作的复杂度。实际上，这是skiplist的一个很重要的特性，这让它在插入性能上明显优于平衡树的方案。这在后面我们还会提到。
根据上图中的skiplist结构，我们很容易理解这种数据结构的名字的由来。skiplist，翻译成中文，可以翻译成“跳表”或“跳跃表”，指的就是除了最下面第1层链表之外，它会产生若干层稀疏的链表，这些链表里面的指针故意跳过了一些节点（而且越高层的链表跳过的节点越多）。这就使得我们在查找数据的时候能够先在高层的链表中进行查找，然后逐层降低，最终降到第1层链表来精确地确定数据位置。在这个过程中，我们跳过了一些节点，从而也就加快了查找速度。

跳表是如何查询的

刚刚创建的这个skiplist总共包含4层链表，现在假设我们在它里面依然查找23，下图给出了查找路径：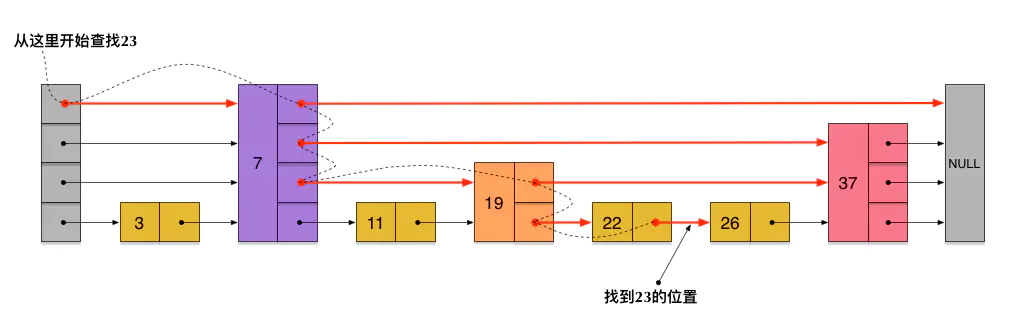

需要注意的是，前面演示的各个节点的插入过程，实际上在插入之前也要先经历一个类似的查找过程，在确定插入位置后，再完成插入操作。
至此，skiplist的查找和插入操作，我们已经很清楚了。而删除操作与插入操作类似，我们也很容易想象出来。这些操作我们也应该能很容易地用代码实现出来。
当然，实际应用中的skiplist每个节点应该包含key和value两部分。前面的描述中我们没有具体区分key和value，但实际上列表中是按照key进行排序的，查找过程也是根据key在比较。

skoplist如何随机出层数

如果你是第一次接触skiplist，那么一定会产生一个疑问：节点插入时随机出一个层数，仅仅依靠这样一个简单的随机数操作而构建出来的多层链表结构，能保证它有一个良好的查找性能吗？为了回答这个疑问，我们需要分析skiplist的统计性能。
在分析之前，我们还需要着重指出的是，执行插入操作时计算随机数的过程，是一个很关键的过程，它对skiplist的统计特性有着很重要的影响。这并不是一个普通的服从均匀分布的随机数，它的计算过程如下：

• 首先，每个节点肯定都有第1层指针（每个节点都在第1层链表里）。
• 如果一个节点有第i层(i>=1)指针（即节点已经在第1层到第i层链表中），那么它有第(i+1)层指针的概率为p。
• 节点最大的层数不允许超过一个最大值，记为MaxLevel。

这个计算随机层数的代码如下所示：

int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
#define ZSKIPLIST_MAXLEVEL 32
#define ZSKIPLIST_P 0.25

直观上期望的目标是 50% 的概率被分配到 Level 1，25% 的概率被分配到 Level 2，12.5% 的概率被分配到 Level 3，以此类推…有 2-63 的概率被分配到最顶层，因为这里每一层的晋升率都是 50%。

Redis 跳跃表默认允许最大的层数是 32，被源码中 ZSKIPLIST_MAXLEVEL 定义，当Level[0] 有 264 个元素时，才能达到 32 层，所以定义 32 完全够用了。

skiplist 跳表

跳表skipList在Redis中的运用场景只有一个，那就是作为有序列表zset的底层实现。跳表可以保证增、删、查等操作时的时间复杂度为O(logN)，这个性能可以与平衡树相媲美，但实现方式上却更加简单，唯一美中不足的就是跳表占用的空间比较大，其实就是一种空间换时间的思想。跳表的结构如下所示：

Redis中跳表一个节点最高可以达到64层，一个跳表中最多可以存储2^64个元素。跳表中，每个节点都是一个skiplistNode，
每个跳表的节点也都会维护着一个score值，这个值在跳表中是按照从小到大的顺序排列好的。

表头结构zskiplist

https://github.com/redis/redis/blob/6.0/src/server.h

跳表的结构定义如下所示：

typedf struct zskiplist{
    //头节点
    struct zskiplistNode *header;
    //尾节点
    struct zskiplistNode *tail;
    // 跳表中元素个数
    unsigned long length;
    //目前表内节点的最大层数
    int level;
}zskiplist;

header：指向跳表的头节点，通过这个指针可以直接找到表头，时间复杂度为O(1)；
tail：指向跳表的尾节点，通过这个指针可以直接找到表尾，时间复杂度为o(1)；
length：记录跳表的长度，即不包括头节点，整个跳表中有多少个元素；
level：记录当前跳表内，所有节点中层数最大的level；

zskiplistNode 具体数据节点

zskiplistNode的结构定义如下：

typedf struct zskiplistNode{
    sds ele;// 具体的数据
    double score;// 分数
    struct zskiplistNode *backward;//后退指针
    struct zskiplistLevel{  
        struct zskiplistNode *forward;//前进指针forward
        unsigned int span;//跨度span
    }level[];//层级数组 最大32
}zskiplistNode;

• ele：真正的数据，每个节点的数据都是唯一的，但节点的分数score可以是一样的。两个相同分数score的节点是按照元素的字典序进行排列的；
• score：各个节点中的数字是节点所保存的分数score，在跳表中，节点按照各自所保存的分数从小到大排列；
• backward：用于从表尾向表头遍历，每个节点只有一个后退指针，即每次只能后退一步；

• 层级数组：这个数组中的每个节点都有两个属性，forward指向下一个节点，span跨度用来计算当前节点在跳表中的一个排名，这就为zset提供了一个查看排名的方法。数组中的每个节点中用1、2、3等字样标记节点的各个层，L1代表第一层，L2代表第二层，L3代表第三层；，以此类推；

  skiplist与平衡树、哈希表的比较

• skiplist和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点。

• 在做范围查找的时候，平衡树比skiplist操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第1层链表进行若干步的遍历就可以实现。
• 平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而skiplist的插入和删除只需要修改相邻节点的指针，操作简单又快速。
• 从内存占用上来说，skiplist比平衡树更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而skiplist每个节点包含的指针数目平均为1/(1-p)，具体取决于参数p的大小。如果像Redis里的实现一样，取p=1/4，那么平均每个节点包含1.33个指针，比平衡树更有优势。
• 查找单个key，skiplist和平衡树的时间复杂度都为O(log n)，大体相当；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。所以我们平常使用的各种Map或dictionary结构，大都是基于哈希表实现的。
• 从算法实现难度上来比较，skiplist比平衡树要简单得多。

  Redis为什么用skiplist而不用平衡树？

  在前面我们对于skiplist和平衡树、哈希表的比较中，其实已经不难看出Redis里使用skiplist而不用平衡树的原因了。现在我们看看，对于这个问题，Redis的作者 @antirez 是怎么说的：

  https://news.ycombinator.com/item?id=1171423 There are a few reasons:

  1. They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
  2. A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
  3. They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

这里从内存占用、对范围查找的支持和实现难易程度这三方面总结的原因，我们在前面其实也都涉及到了。