1、离散/连续随机变量、概率函数

• 对于随机变量，均有概率，即有对应的分布特征。
• Probability Distribution（概率分布）
  • Specifies the probabilities of the possible outcomes of a random variable.
• Discrete/Continuous random variables（离散/连续随机变量）
  • Discrete random variables（离散随机变量）
    • take on at most a countable number of possible outcomes but do not necessarily to be limited.
    • 取值可数
  • Continuous random variables（连续随机变量）
    • cannot describe the possible outcomes of a continuous random variablewith a listbecause the outcomenot in the list, would always be possible.
    • 取值不可数
    • 特征：
      • （even thoughcan happen）
      • （计算概率时通常是计算区间的概率）
• Probability function（概率函数）
  • For discrete random variables
  • 
  • 
• Probability density function（PDF，概率密度函数）
  • For continuous random variable commonly.
  • 用密度函数图形的面积表示概率（以下为正太分布的概率密度函数）

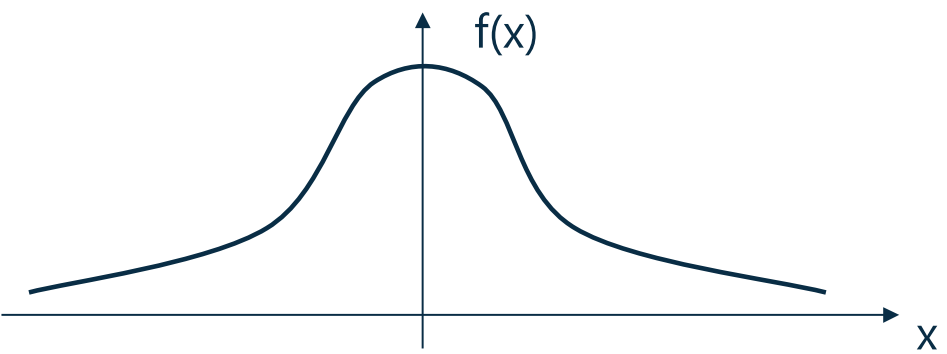
• Cumulative probability function（CPF，累积概率函数）
  • 

2、概率分布：离散分布（2 种）

（1）Discrete uniform distribution（离散均匀分布）

• A known, finite number of outcomes equally likely to happen.（取值确定、取值概率相等）
• Every one ofoutcomes has equal probability

• 如：Rolling a dice will have 6 possible outcomes as，the probability of each outcome is 0.167

  （2）Binomial distribution（二项式分布）

• Bernoulli random variable（伯努利随机变量）

  • 
  • 
  • 一个事件只有两种结果的情况（如抛硬币，结果只能是正面 or 反面）
• Binomial random variable（二项式随机变量）
  • the probability ofsuccesses intrails
  • 
  • 如：计算抛次硬币，有次正面朝上（假设代表成功）的概率（每次实验都相互独立，且每次实验均只能有两种结果）
    • 次实验
      • 次成功，成功的概率用表示
      • 次不成功
    • 公式原理：从次实验中挑选出次（即：），乘以其概率，剩下的次均为不成功的，其概率为，相乘即为所求概率。
  • 应用：可应用到预测生孩子判断性别概率上，如：医院里当天生个孩子，求生出个男孩的概率
• 伯努利随机变量 vs 二项式随机变量
  • 相同点：事件均只有两种结果
  • 不同点：
    • 伯努利随机变量中，只做一次实验
    • 二项式随机变量中，做了 n 次实验
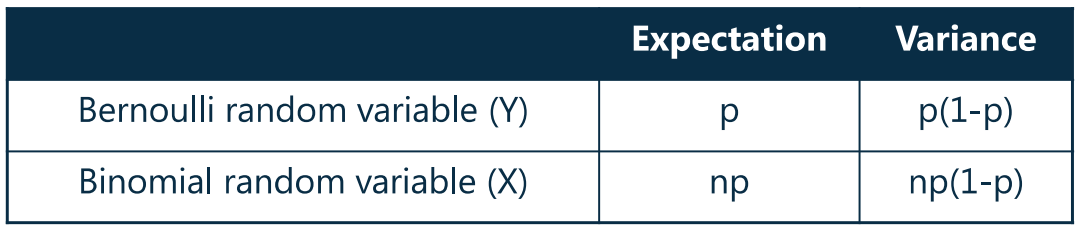
  • Expectations（期望）、variances（方差）【了解，不太考，推导见视频】

3、概率分布：连续分布（3 种）

（1）Continuous Uniform Distribution（连续均匀分布）

• All intervals of the same length on the Continuous Uniform Distribution’s support are equally probable.
  • The support is defined by the two parameters, and, which are its minumum and maximum values.

• 特征：

  • For all：
    • 
  • （不在可选范围内的结果的概率均为 0）

    （2）Normal distribution（正太分布）

    

• 特征：

  • （决定正太分布的变量：均值和方差）
  • Symmetrical distribution：skewness=0, kurtosis=3
    • 密度函数的图形形状对称
  • A linear combination of normally distributed random variables is also normally distributed.
    • 如果和均服从正太分布，则他们的线性组合也符合正太分布
  • The tails get thin and go to zero but extend iinfinitely, asympotic（渐近）

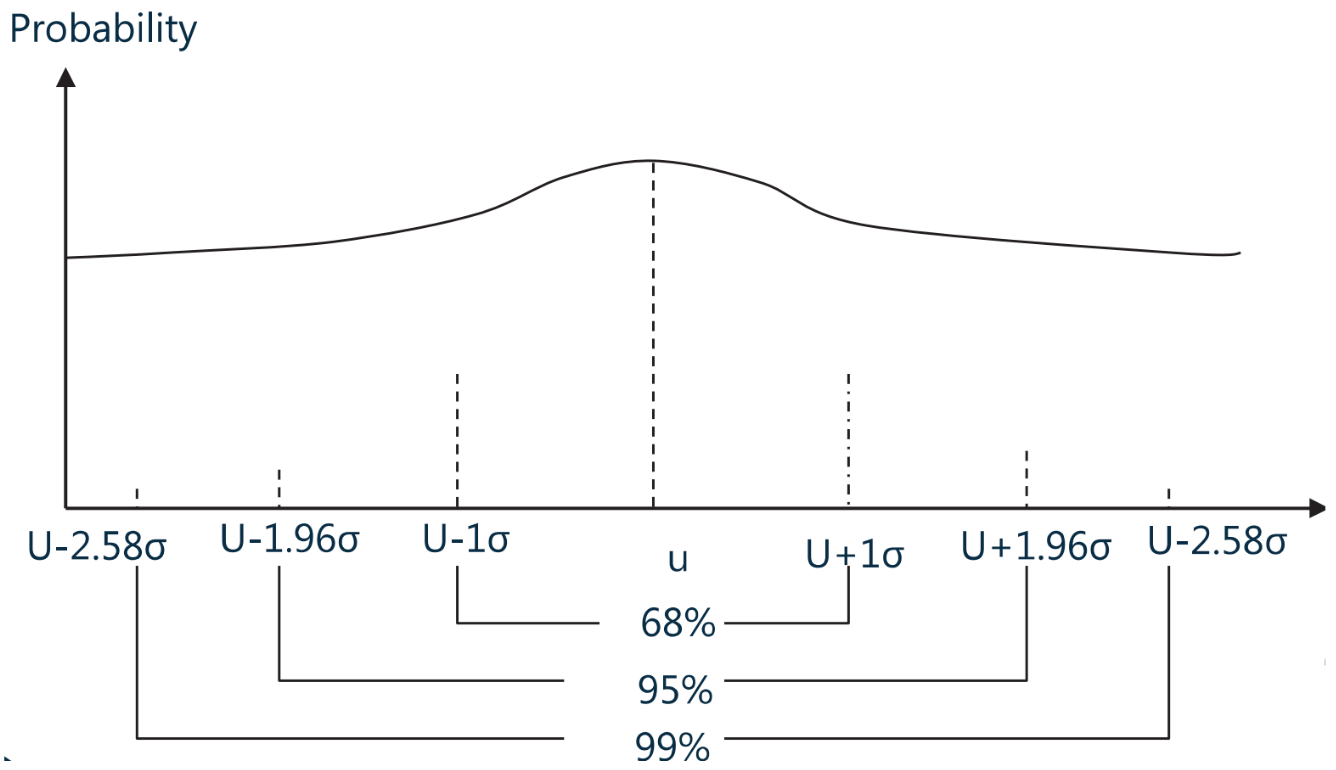
    （a）Confidence intervals（置信区间，正太分布的置信区间）

• 置信区间：个体落在某个区间的概率有多大（一个区间对应一个概率）

• 68% confidence interval is
• 90% confidence interval is
• 95% confidence interval is
• 99% confidence interval is

• 之前讲过的切比雪夫不等式对于任何分布均成立，其含义为：

  • 
  • 如，正太分布中，

    （b）标准正太分布（standard normal distribution）

• 标准正太分布：or

• standardization（普通正太分布的标准化）：
  • 如果，则
  • 推导：
    • 如果，则：
      • 
      • 
      • 
    • 如果，则：
      • 
      • （一组数据同时加上一个数，不会影响其离散程度）
      • 
• 为什么要进行标准化？
  • 方便查表（Z-table 表）；统计学家不可能做无数个正太分布表。
    • 
    • 
    • 
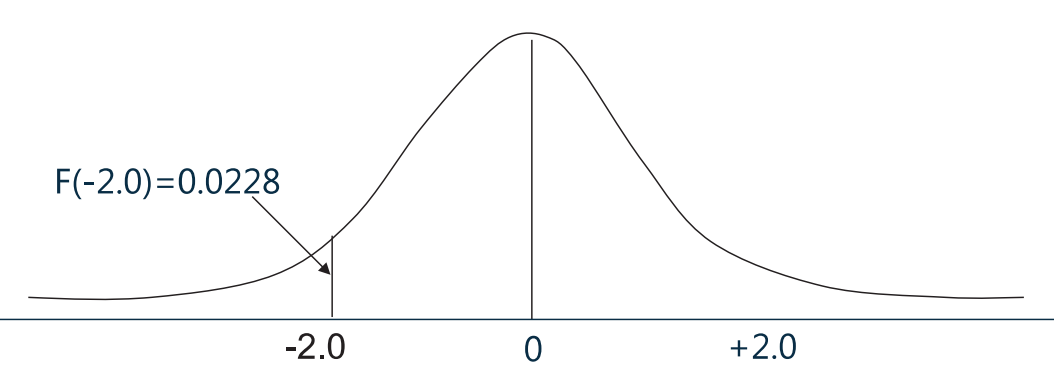
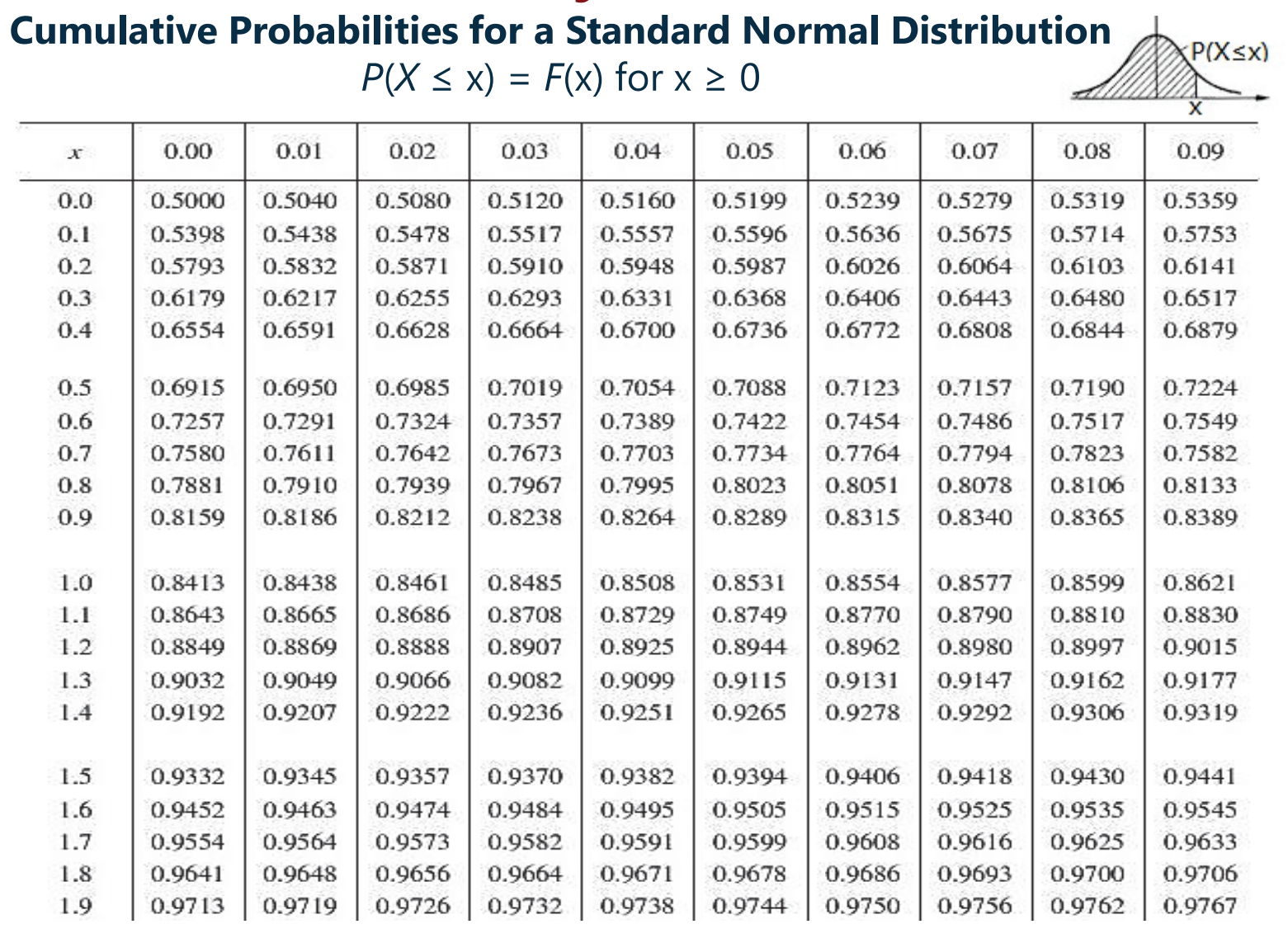
  • Z-table 表如下（每个数值均为累积概率，只给出了的部分，另外一部分对称）：

• 常见考法：

  • 给定，求
    • 先进行标准化：
      • 
      • 
  • 计算
    • 画图，基于对称原理，可得：
  • 计算
    • 画图，基于对称原理，可得：
      • 

        （c）名词概念：Shortfall risk、Roy’s safety-first criterion、Maximize S-F-Ratio

• Shortfall risk

  • ：threshold level return、minimum return required
  • 如果，出现这种情况的概率（），即为 Shortfall risk
  • 即：基金经理做投资的回报率小于客户最底要求回报率的风险
  • 越小越好
• Roy’s safety-first criterion
  • 
  • 类似夏普比率，但此处的基准是（客户要求的最低回报率），而夏普比率的基准为（无风险回报率）
  • 越大越好

• Maximize S-F-Ratio

  • 如果越大，则越小

    （3）lognormal distribution（对数正太分布）

• Ifis normal, thenis lognormal.

  • 如果是正太分布，则服从对数正太分布（注意：不能颠倒说法）
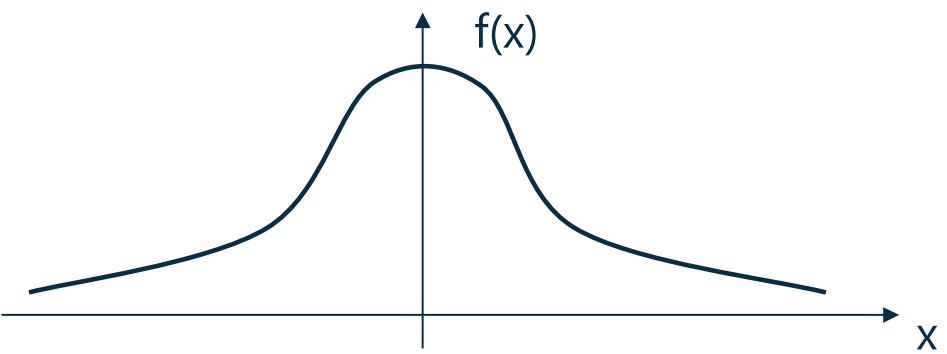
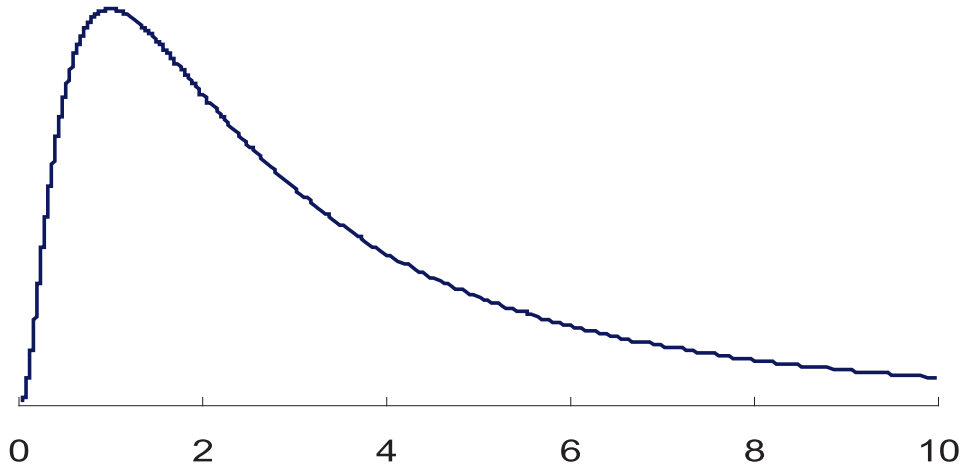
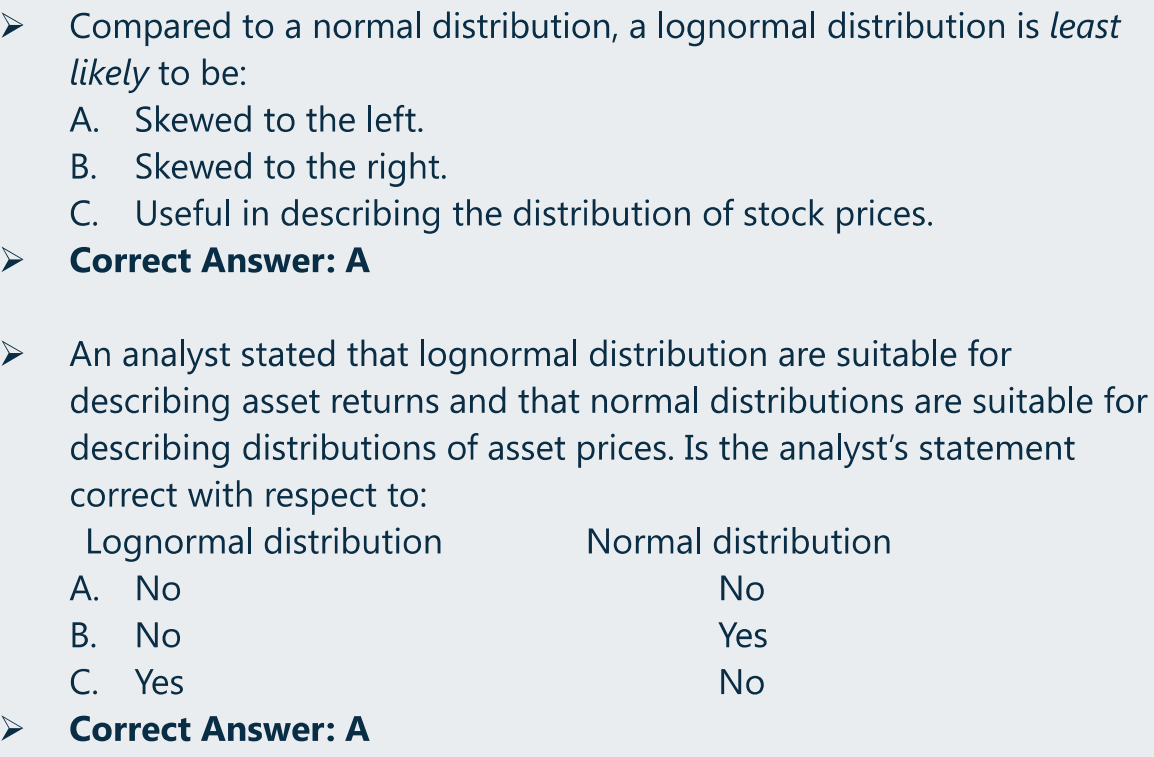
• 特点：Right skewed（右偏）.
  • 考试时，可能会与偏度的相关概念与特性结合起来考
• The values of random variables that follow lognormal distribution are always be positive, so it is useful for modeling asset prices.
  • 资产价格（P）总是大于 0 的，因此实际应用中总是假设资产价格符合对数正太分布。
  • 而 Return 可以小于 0 或大于 0，与正太分布的特性相似，故实际应用中假设 Return 是符合正太分布的。

4、Monte Carlo simulation、Historical simulation

• 离散（Discrete）
  • 
• 连续（Continuous）
  • 
• （持有一年）
• （持有 T 年）
• Monte Carlo simulation
  • generate a large number of random samples from specified probability distribution(s) to represent the operation of risk in the system.
  • It is used in planning, in financial risk management, and in valuing complex securities.
  • Limitations：
    • The operating of Monte Carlo simulation is very complex and we must assume a parameter distribution in advance.
    • Monte Carlo simulation provides only statistical estimates, not exact results.

• Historical simulation

  • repeat sampling from a historical data series.
  • grounded in actual data but can reflect only risks represented in the sample historical data.
  • Compared with Monte Carlo simulation, historical simulation does not lend itself to “what if” analyses.

    5、例题

    （1）离散/连续随机变量、概率函数、概率分布

    （a）离散型随机变量的概率分布

    

    （b）连续均匀分布、累积分布函数

    

    （c）概率分布的理解：离散均匀分布

    

    （d）二项式分布求概率公式

    

    （e）二项式分布：求期望 E(X)

    

    （f）二项式分布：概念理解

    

    （2）连续分布

    （a）连续均匀分布

    

    （b）正太分布：Confidence intervals

    

    （c）正太分布：基于区间范围计算均值和标准差

    

    （d）标准正太分布：概率计算

    

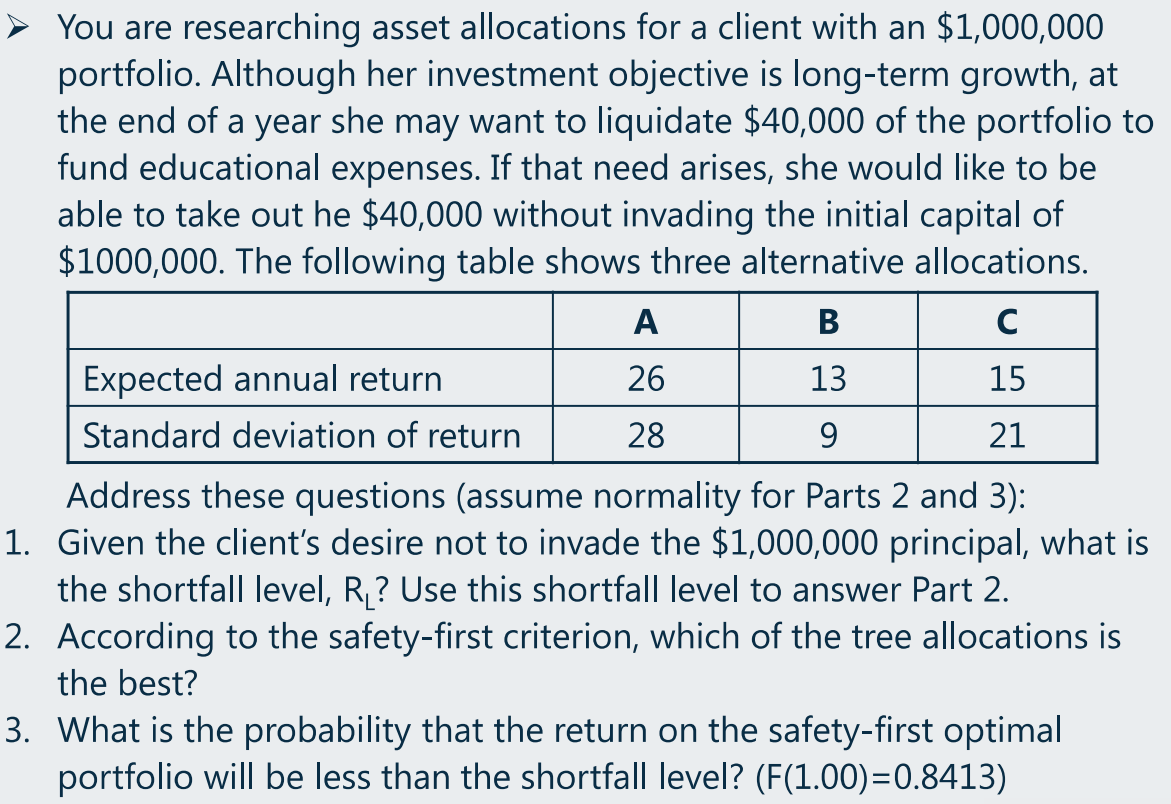
    （e）Shortfall risk、Roy’s safety-first criterion、Maximize S-F-Ratio

    Roy’s safety-first criterion 计算与比较

    

• 

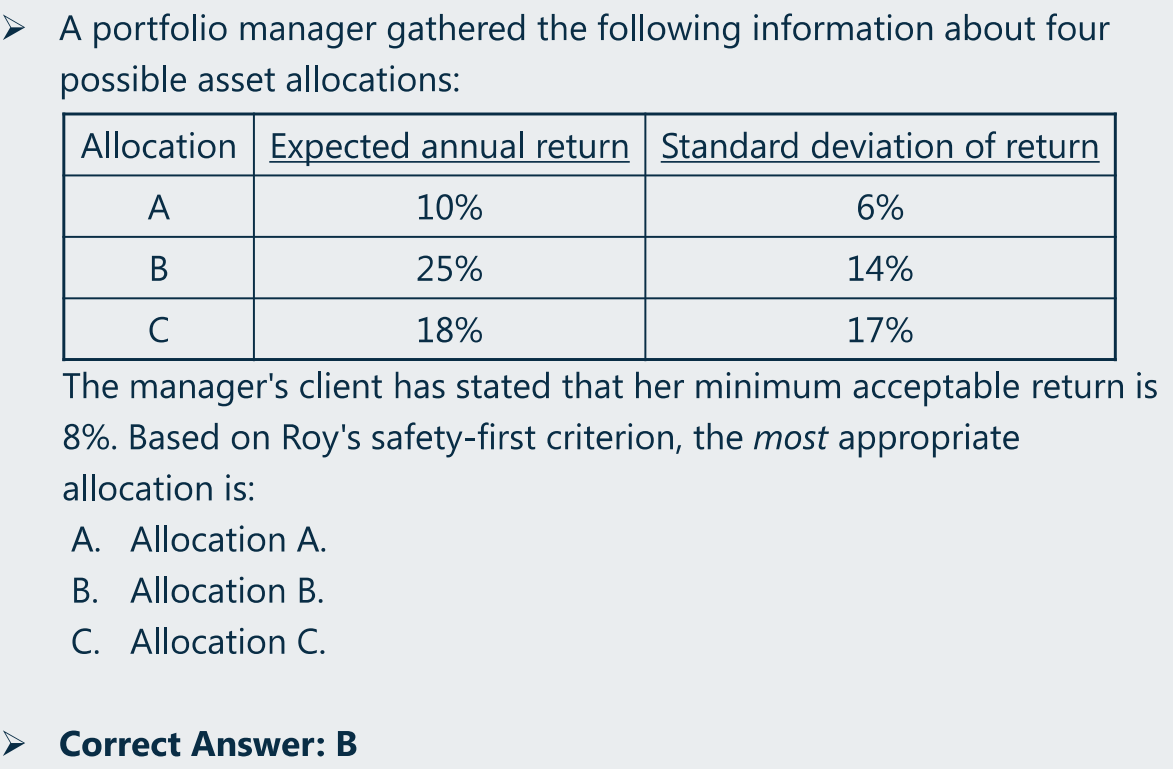
• （求解取最大值即可）

  Shortfall risk 的理解、Roy’s safety-first criterion 计算与比较、正太分布概率计算

  
  

  （f）对数正太分布

  

  （3）Monte Carlo simulation