-
1、required rate of return 的各种形式
Required rate of return(要求回报率):the return that investors and savers require to get them to willingly lend their funds
- usually for particular investment
- affected by the supply and demand of funds in the market
- Discount rate(折现率):the interest rate we use to discount payements to be made in the future, usually used interchangeably with the interest rate.
- 不同时间点的钱不能直接比较(钱具有时间价值),应该折现到同一时间点(依靠折现率进行折现)。
- Opportunity cost(机会成本): the value that investors forgo by choosing a particular course of action
- 选择当前投资而放弃的其它最优投资,其它的最优投资即为机会成本。
- also understood as a form of interest rate.
Required rate of return 的分解
- Nominal risk-free rate = real risk-free rate + expected inflation rate(费雪方程式)
- 市场上能看到的利率,均为 Nominal(名义)利率
- CFA 中认为美国国债没有风险,因此,美国国债对应的利率即 risk-free rate
- 任何一个产品的要求回报率都等于一个无风险利率加上相应的风险溢价(只要承担风险,就需要得到风险溢价)
- Required interest rate on a security = nominal risk-free rate + default risk(违约风险)premium+ liquidity(流动性)risk premium + maturity(期限)risk premium
单利:只有本金参与计息,利息不再参与计息(一年按 360 天计算)
- 复利:本金和利息均参与计息(一年按 365 天计算)
- 后续均为复利,除非特别指出
- Effective Annual Rate(有效年利率):投资 n 年,按利滚利的形式计算一年实实在在的年化收益率(一年可能计息多次)
- 示例:1 块钱,投资一年,假设年利率为 10%:
- 一年计息 1 次:
- 一年计息 2 次:
- 即半年计息一次,半年利息为
- 即半年计息一次,半年利息为
- 一年计息 4 次:
- 一年计息 365 次:
- 一年计息 m 次:
- 注意:
- 是一年计息 m 次,得到的才是有效年利率(不是 n 年计息 m 次)
- 如果要求计算 m,则采用试错法求解
- 当 m 趋向于无穷大时,求极限可得
为年利率,当
时,
- 特点:m 越大(一年计息次数越多),EAR 越大
- 一年计息 1 次:
- 示例:1 块钱,投资一年,假设年利率为 10%:
- FV(Future value):amount to which investment grows after one or more compounding periods
- PV(Present value):Current value of some future cash flow
3、Annuities(年金)
(1)定义
- 符合以下特征的有限时间序列现金流(a finite set of level sequential cash flows)即为年金:
- 等时间间隔
- 等现金流
- 相同方向
- 年金示例:
- 等额还房贷
- 等额还租金
金融计算器计算年金:
如 3 年,每年年末得 100,则:
the first cash flow occurs immediately,at t=0
- 案例:租金(rental fees)、学费(tuition fees)、生活费(living expenses)
如 3 年,每年年初得 100,则:
- 可通过金融计算器计算,计算时 FV 设置为 0,即可求 PV
- 可通过金融计算器计算,计算时 PV 设置为 0,即可求 FV
- 如果使用计算器计算,需要先调整计算器为先付年金模式 BGN(默认为后付年金模式,END)
- 按 2ND + PMT 可查看当前模式(默认为 END)
- 按 2ND + ENTER(即 SET)可切换模式
- 先付年金的 FV 和 PV 均比相应的后付年金的大 (1+ I/Y) 倍
perpetuity(永续年金):a financial instruments that pays a fixed amount of money at set intervals over an infinite period of time.
- 特殊的后付年金:现金流发生在每一期期末,且永续无限
- 时间永续,因此没办法求 FV,只能求 PV
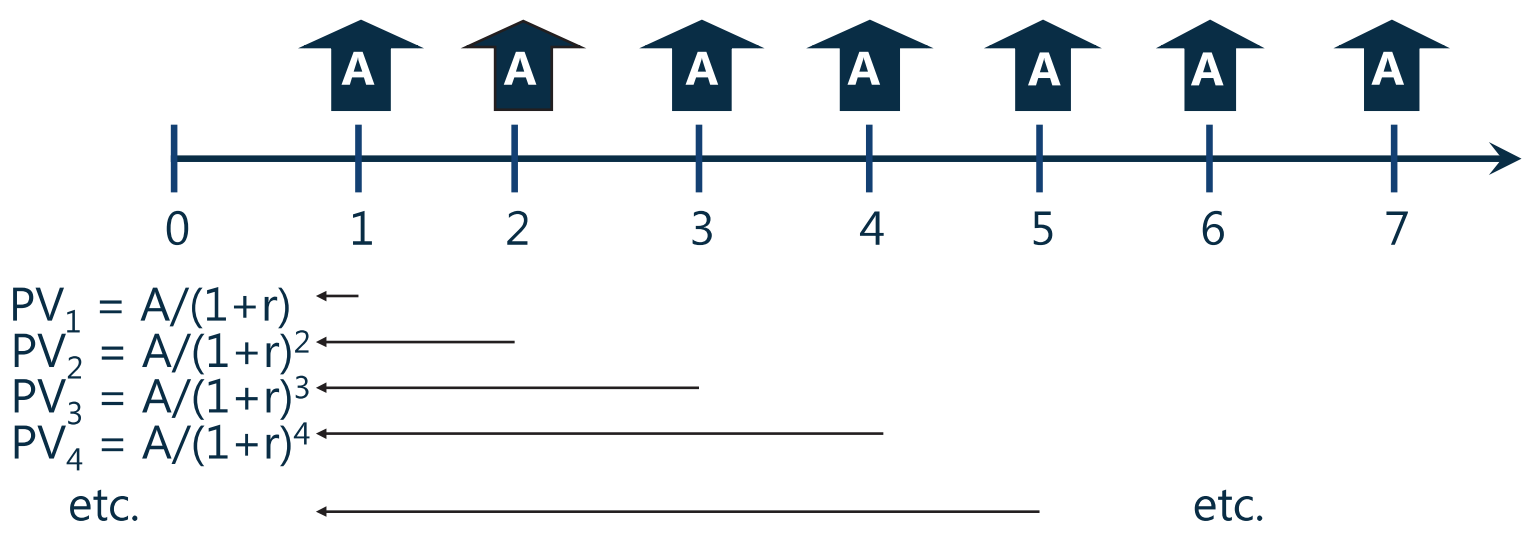
- 推导公式
- 两边同乘以
得:
- 两式相减,且忽略等号右边最后一项(接近无穷小),可得:
- 因此:
应用:优先股、永续债
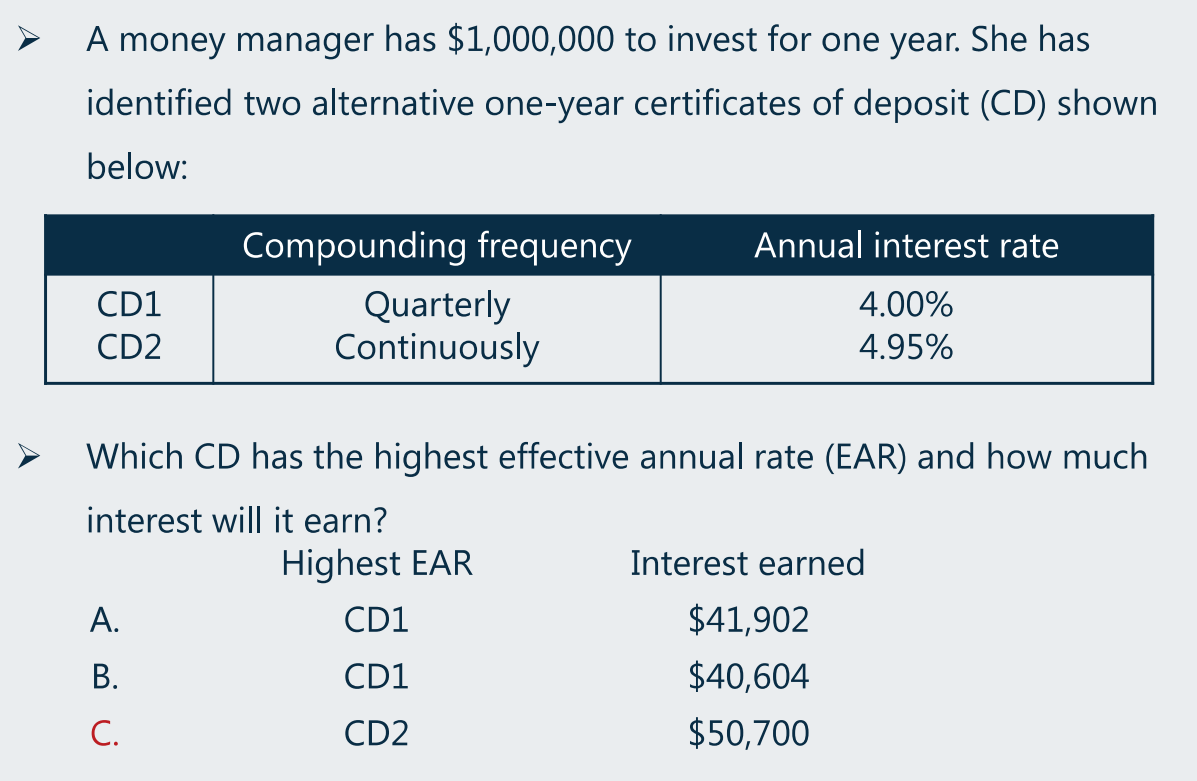
CD2 是连续付利,公式:
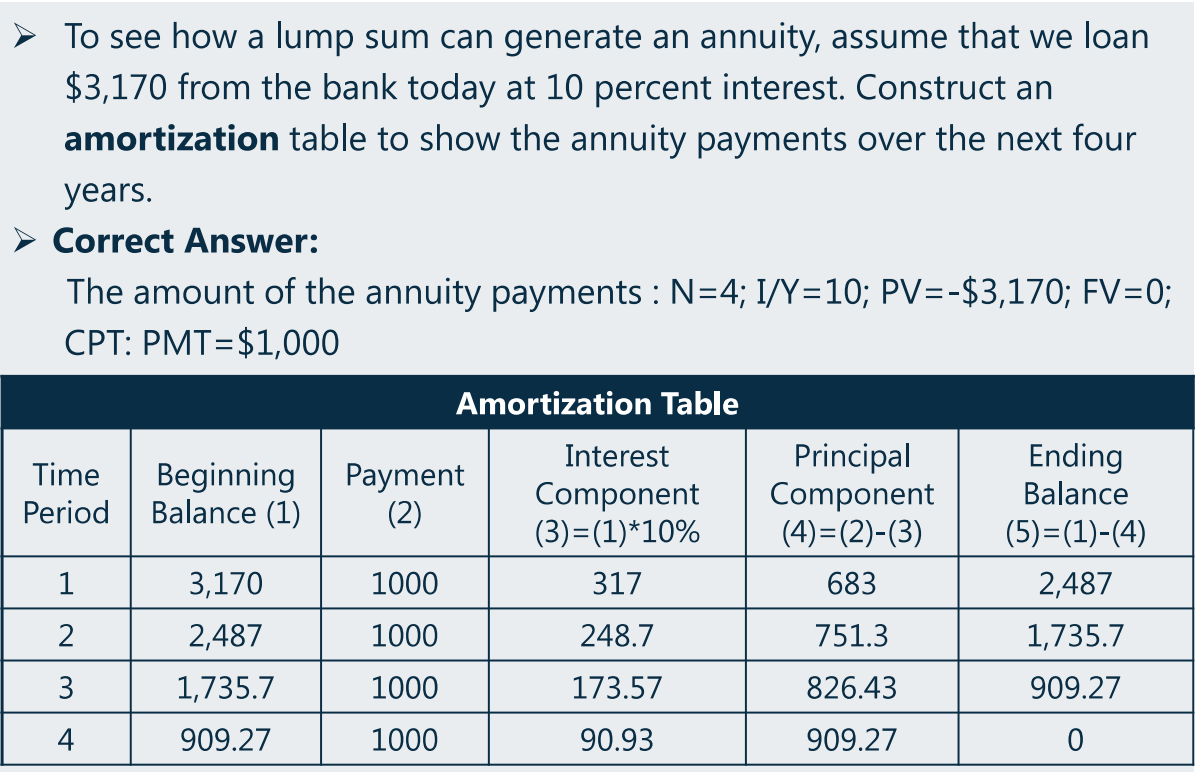
从银行中以 10% 的利率贷款 3170,银行要求每年还款 1000,还 4 年。写出这 4 年的 amortization table(摊还表)
- 此示例是提前算好的,即贷款 3170 每年还 1000,还 4 年,对应的贷款利率就是 10%。此处是为了方便摊还表的计算,故提前告诉你贷款利率是 10%。
- 金融计算器中的摊销功能(使用摊销功能时,必须选计算一次年金的各个项:N、I/Y、PV、FV、PMY,知 4 求 1):
- 2ND + PV(即 AMORT)
- P1:开始时期
- P2:结束时期
- 如果 P1=P2=1,则表示从第一期的开始,到第一期结束(即 0-1)
- 如果 P1=P2=2,则表示从第二期的开始,到第二期结束(即 1-2)
- 如果 P1=1,P2=2,则表示从第一期的开始,到第二期结束(即 0-2)
- BAL:即代表对应时间段下的 Ending Balance(还有多少钱没还)
- PRN:P1 与 P2 确定的时间段内,摊还的本金部分
- INT:P1 与 P2 确定的时间段内,摊还的利息部分
- 2ND + PV(即 AMORT)
可见:等额还款形式,最开始摊还时的利息最多(因为最开始欠的钱最多),相应的摊还的本金部分最少;随后摊还的利息逐渐变少(因为随着摊还,欠的钱已经越来越少),相应摊还的本金部分越多。
对于求解所有年金题目,先画现金流量图。
- 本题为先付年金与后付年金的结合【IMP】
- 注意:养老金与教育金类似