1、描述性统计学、推断性统计学
2、Types of measurement scales
3、样本、总体、频率分布
4、各种统计指标（均值等）、应用
5、Quantiles（分位数）
6、Absolute dispersion
7、切比雪夫不等式、变异系数、夏普比率【必考】
8、skew（symmetrical、positive、negative）
9、峰度（kurtosis）：Leptokurtic、platykurtic
10、例题

1、描述性统计学、推断性统计学

Descriptive statistics（描述性统计学）
- Quantitatively describe or summarize the important features of large data sets.
- 当拿到一组数据之后，分析这组数据的特征，有 4 个维度：
  - mean（均值）：看数据在哪个数的周围，衡量中心趋势
  - variance（方差）：看数据的离散程度，是比较集中，还是比较分散？
  - skewness（偏度）：画图、看数据的对称程度，对称？偏左？偏右？
  - kurtosis（峰度）：数据的最大部分的值
- 偏向于对数据的描述、统计分析（descriptive）
Inferential statistics（推断性统计学）
- Makes estimations about a large set of data（a population with smaller group of data）
- 用样本推断总体，涉及抽样估计
  - 如：判断下中国人的平均身高，不可能所有人都量一遍，需要抽样统计、推断。
- 偏向于推断
  2、Types of measurement scales
数据抽出来后，需要分类别，以下介绍 4 种类型（知道对应的特征即可）。
Nominal Scales
- Distinguishing two different things, no order, only has mode.
- 定义类别而已，如把男生定义为 1，女生定义为 2（不能比较大小）
Ordinal scales（>、<）
- Making things in order（排序）, but the difference are not meaningful.
- 如：ranking mutual funds based on their five-year cumulative returns, we might assign the number top-1 to 10 for the funds performance.
Interval scales（>、<、+、-）
- Subtract is meaningful
- 间隔、间距，在排序的基础上可进行加减运算（但不能乘除、算比例）
- 如：温度（temperature），哈尔滨温度 -10，北京 0，上海 10
Ratio Scales（>、<、+、-、*、/）
- with original point.（比率，在加减的基础上，扩充了乘除运算）
- 如：money. If we have twice as much money, then we have twice the purchasing power.
  3、样本、总体、频率分布
population（总体）
- A population is defined as all members of a specified group.
- A parameter is used to describe the features of a population.
  - 描述总体的方差、均值等，均叫总体的参数
sample（样本）
- A sample is a subset of a population.
- A sample statistic is used to describes the features of a sample.
  - 描述样本的方差、均值等，叫样本的统计量
  - sample size：样本的大小
  - 如抽样 100 人统计平均身高，则样本有 1 个，样本的大小为 100
frequency distribution（频率分布）
- 示例-1：
  - 假设统计全班 20 人的身高分布，大致为 150-180
    - 150-160：10
    - 160-170：5
    - 170-180：5
  - 以上分三组，每组间隔为 10，每一组的间隔称 relative interval
  - 每组的人数即为绝对频率（absolute frequency）
  - 每组人数在总体的占比即相对频率（relative frequency），代表相对占比情况
- 示例-2：

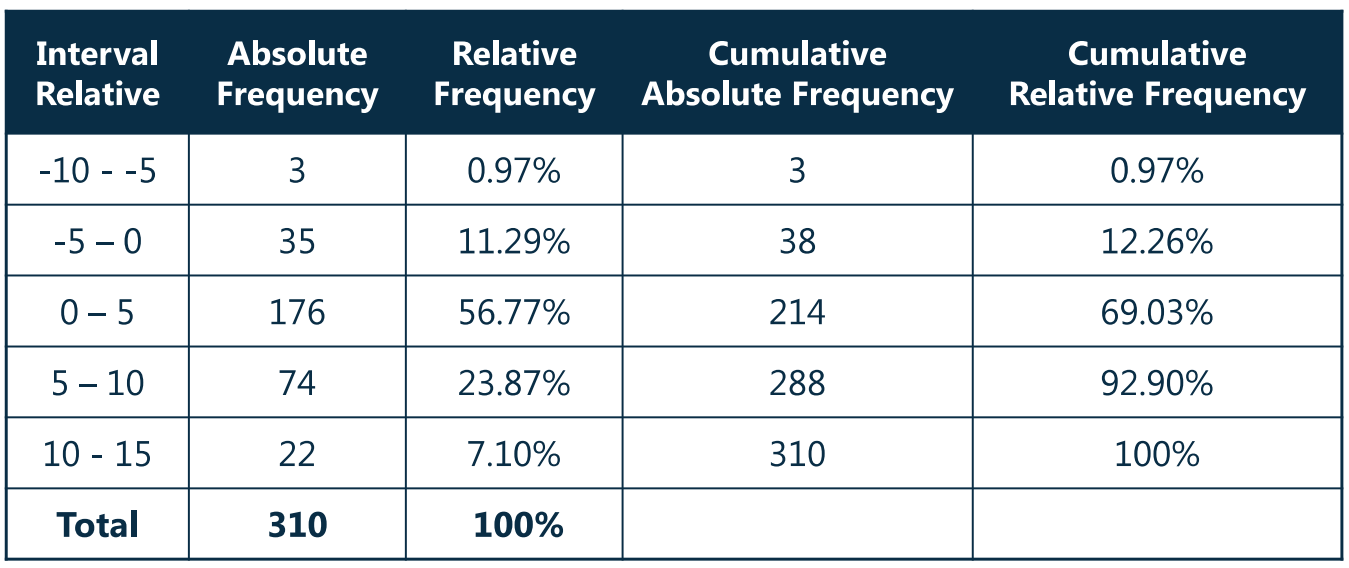
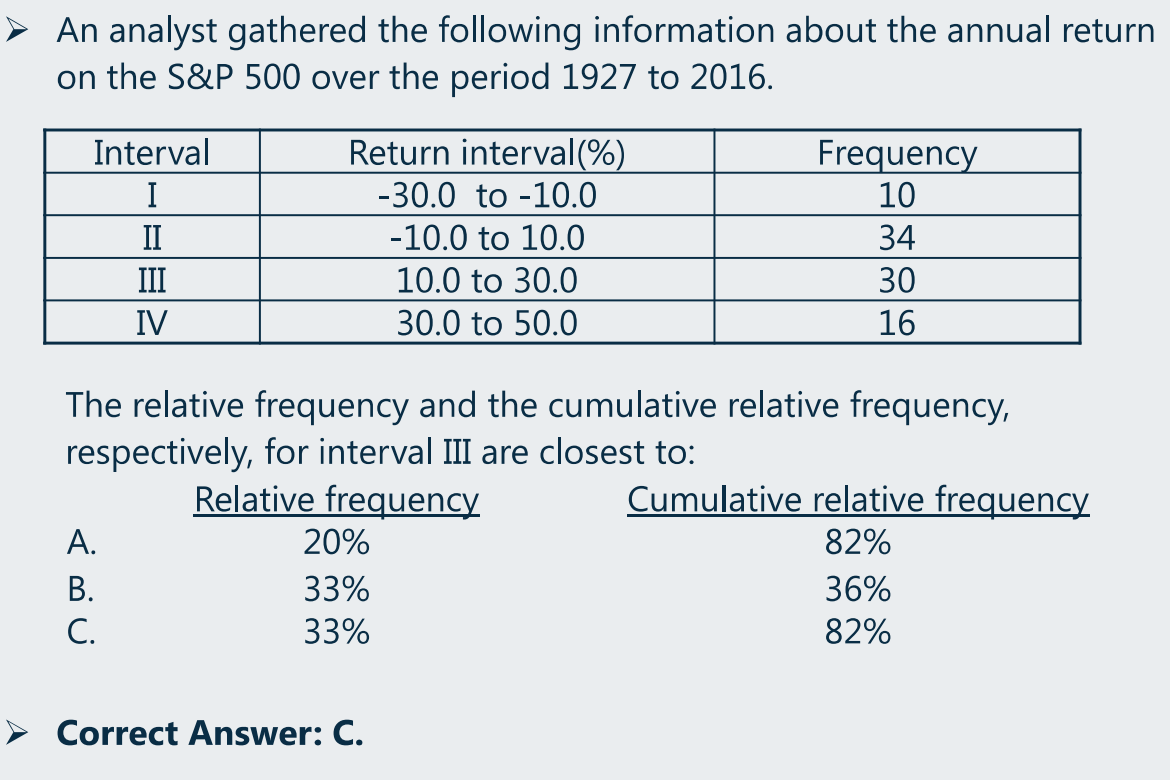
Relative frequency
- The relative frequency of observations in an interval is the number of observations（the absolute frequency）in the interval divided by the total number of observations.
Frequency Distribution
- A frequency distribution is a tabular display of data summarized into a relatively small number of intervals.
- Frequency distributions permit analyst to evaluate how data are distributed.
Cumulative frequency、Cumulative Relative Frequency
- The cumulative relative frequency cumulates（adds up）the relative frequencies as we move from the first interval to the last.
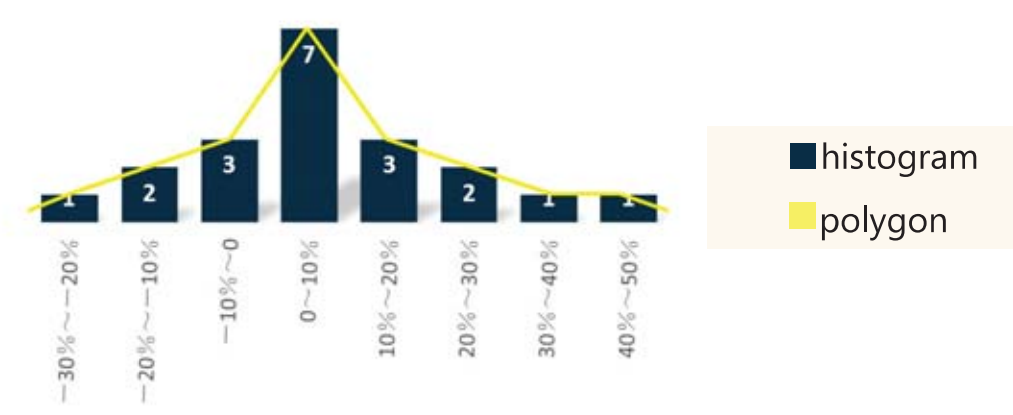
  - Histogram and Polygon
A histogram is a bar chart of data that have been grouped into a frequency distribution.
A frequency polygon is a graph of frequency distributions obtained by drawing straight lines joining successive points representing the class frequencies.

4、各种统计指标（均值等）、应用

mode：众数（出现次数最多的数）
median：中位数（排序后取中间值）
mean：均值，有多种均值衡量方式
- Arithmetic mean（算术平均）
  - 每个数值的权重均为
- Weighted mean（加权平均）
  - 算术平均为加权平均的特例
- Geometric mean（几何平均）
  - 主要用于收益率计算
    - 收益率加 1，随后开根号后减 1
- Harmonic mean（调和平均）
  - 应用：假设购买 3 只股票，每只购买相同的金额 1，但每只股票的股价各不相同，分别为 P1、P2、P3，现在想计算花了 3 块钱购买股票的平均股价是多少？
    - 总体思路：平均股价 = 花的金额总数/购买到的总的股票份额
- 不同均值之间的关系：
  - Harmonic mean <= Geometric mean <= Arithmetic mean
  - 当且仅当数值均相同时，三个值相等
  - 记忆技巧：A >= G >= H（英文字母顺序倒过来）
The use of arithmetic mean and geometric mean when determining investment returns.
- The arithmetic mean is the statistically best extimator of the next year’s returns given only the three years of return outcomes.
- Since past annual returns are compounded each period, the geometric mean of past annual returns is the appropriate measure of past performance.
  - 几何平均含有复利的思想在里面。
    5、Quantiles（分位数）
类别
- Quartile（四分位）
  - 第 3 个四分位数：排序后，分四份，从左往右的第 3 份的某位数，该数的左边包含了 75% 的数。
- Quintile（五分位），常考，因为该单词最不常见
  - The third quintile：60%，即排序后，某数的左边的个数占总个数的 60%，该数即为第 3 个五分位数
- Deciles（十分位）
- Percentile（百分位）
相关计算：
- 从小到大排序，并统计总个数，通过以下公式计算目标所求数值在第几位：
  - - 其中通过描述确定，如第 3 个四分位数，则为
    - 为什么公式中要，而不是？因为是某个数的左边（并不包含该数本身）要包含。
    - 如果该值算出来是小数，则找出整数部分对应的数，以及其下一个数值，并用小数部分乘以这两个数的差值，最后将得到的结果加到整数部分对应的数上。
      6、Absolute dispersion
Absolute dispersion（离散程度）
- the amount of variability present without comparison to any reference point or benchmark.
Range（衡量数值范围）
- Range = maximum value - minumum value
Mean Absolute Deviation
- 代表偏离均值的绝对偏离情况
- 注意：金融计算器没办法计算绝对值
Variance（方差）、Standard deviation
- For population（总体）
  - 方差：
  - 标准差：（方差结果开根号）
- For sample（样本）
  - 方差：
  - 标准差：（方差结果开根号）
- 通常，方差/标准差衡量的是绝对离散程度，后面介绍的 CV 是衡量相对离散程度
- 通常使用样本方差来估计总体方差，样本方差叫做总体方差的无偏估计量，一个好的估计量要符合三个性质，其中一个叫无偏性。由于统计学家发现，求样本方差时，除以是最接近总体方差的，因此求样本方差时就都除以。
- 同时，的自由度为。
  - 自由度（degree of freedom）：一组数据中，必须确定多少个数才能使得这组数据稳定，确定的数的个数即自由度。如：已知 3 数的均值为，此时已经抽取两个数了，由于均值已知，抽取两个数之后，即可确定第 3 个数了，这是抽取的个数为 2 即为这组数的自由度。
- 金融计算器计算方差、标准差
  - 2ND + 7（即 DATA），可以看到 X01 提示
  - 2ND + CE|C（清零，因为之前可能有相关数据）
  - 输入数值，然后按 ENTER，随后按下向下箭头会看到 Y01，暂时不管，是线性回归相关，继续按向下箭头，输入新数值即可。
  - 最后，按 2ND + 8（即 STAT），随后按向下箭头，即可看到总个数、均值、样本的标准差（如果这组数据是样本数据）、总体的标准差（如果这组数据已经是总体数据）
Semivariance、Target Semivariance
- - 衡量小于均值部分的数值的方差
- - B：自定义的 benchmark
    7、切比雪夫不等式、变异系数、夏普比率【必考】
均为均值、标准差的结合
切比雪夫不等式
- For any set of observations（samples or population），the proportion of the values that lie withinstandard deviations of the mean is at least，whereis any constant greater than 1.
  - 对于任何一组观测值，个体落在均值周围个标准差之内的概率不小于（对任意一个的数均成立）。
  - - 个体：
    - 均值：
    - 标准差：
- This relationship applies regardless of the shape of the distribution（对于任何分布，该结论均成立）
- 该不等式表明，对于大部分数，都在均值周围，极端情况都是小概率
- 考试常见考法：
  - 已知，求最小概率（即）
  - 已知、和最小概率（即已知），求范围（即：）
  - 已知总体个数、范围、和（即可求），求在该范围内的个数至少是多少（即：总个数 * 最小概率）
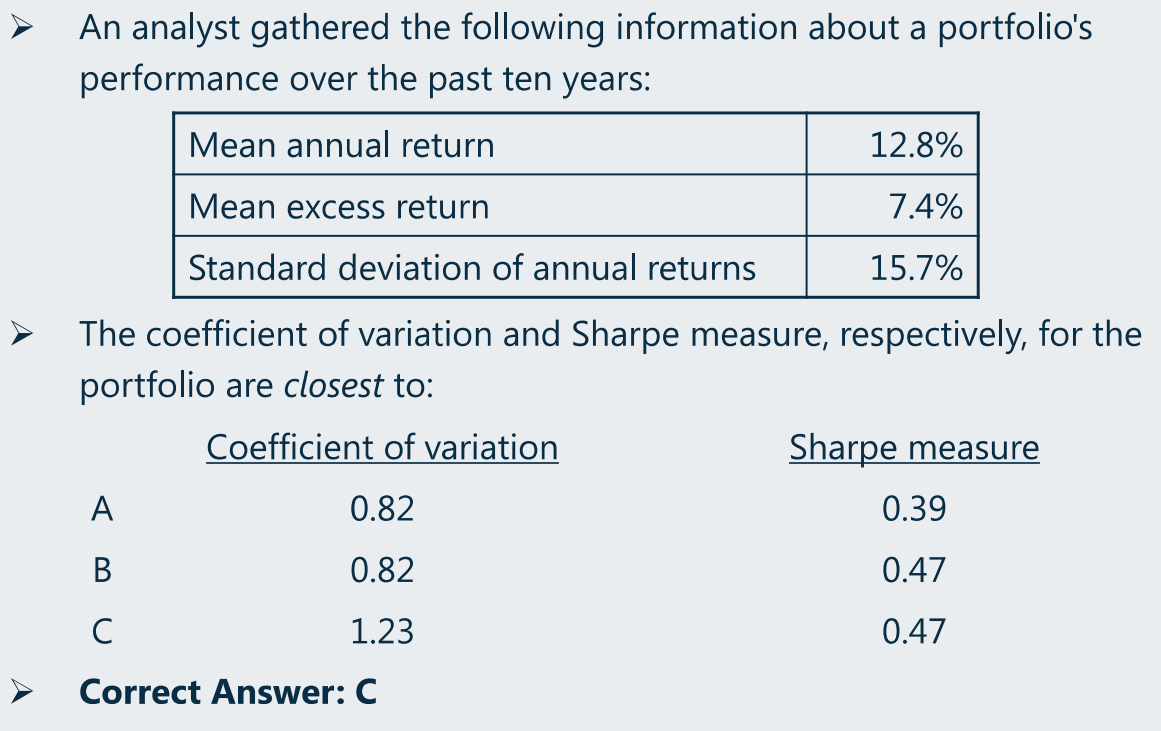
Coefficient of variation（变异系数）
- measures the amount of dispersion in a distribution（即标准差）relative to the distribution’s mean.（relative dispersion）
- 示例：
  - 要求修一段平均 1002 米的路，给三次机会
    - 1001、1002、1003
  - 要求修一段平均 2 米的路，给三次机会
    - 1、2、3
  - 以上两者均达到要求，现在评判下，哪个更好？
    - 当然是上一个更好
    - 使用计算器计算可发现，两组数据的方差/标准差是一样的（即离散程度一样）
    - 可见，方差/标准差并不体现规模程度，CV 计算公式即可体现（用均值表示规模）
- CV 性质：
  - scale-free（剔除了规模因素）
  - 衡量的是相对于均值的离散程度（即 relative dispersion，相对离散程度）
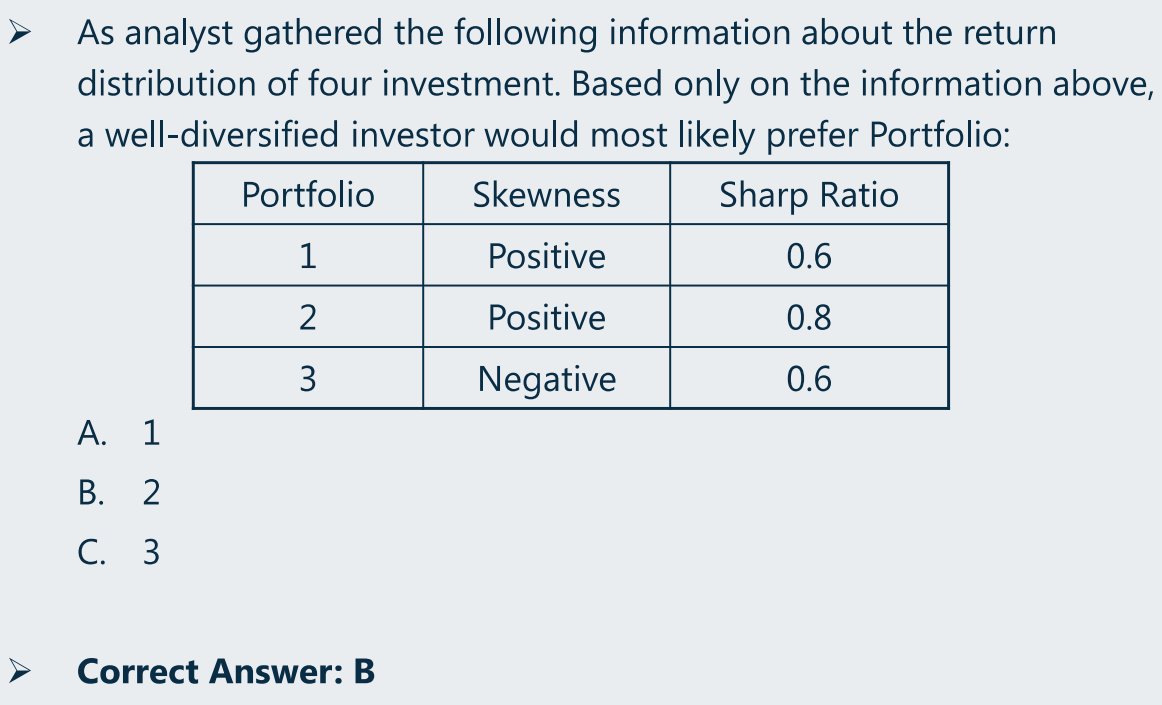
sharp ratio（夏普比率）
- measures excess return per unit of risk.（单位风险的超额回报率，基金经理的业绩衡量指标）
- - 用以衡量风险（风险并不是 Loss，而是不确定性）
    8、skew（symmetrical、positive、negative）
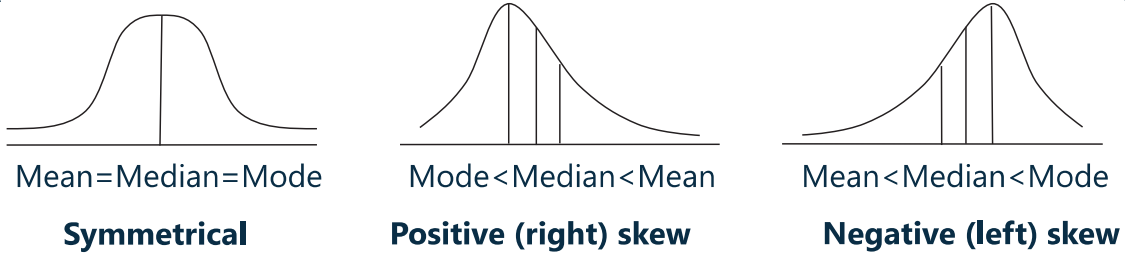
skew（偏度）是最常考的概念
判断左偏还是右偏
- 看哪边有长长的尾巴，即往哪偏（如右边有长长尾巴，即为右偏）
- 右偏的偏度大于 0（Positive skewed）
  - A return distribution with positive skew has frequent small losses and a few extreme gains.
  - 坐标轴右侧的值更大，公式计算得到时，更偏向于正数
  - 右偏的均值也最大，故有：
    - Mode（众数）< Median（中位数）< Mean（均值）
- 左偏的偏度小于 0（negative skewed）
  - A return distribution with negative skew has frequent small gains and a few extreme losses.
  - 坐标轴左侧的值更小，公式计算得到时，更偏向于小的数
  - 左偏的情况与右偏相反：
    - Mode（众数）> Median（中位数）> Mean（均值）
假设一支股票的收益率分布如下：
- -30%、10%、10%、10%
- 是左偏还是右偏？（数据已有，最好还是依据计算结果判断）
- mode：10%
- mean：0%
- mean > mode，即左偏
Investors should be attracted by a positive skew because the mean return falls above the median.
样本（Sample）的偏度计算公式（不考，了解）：
- 9、峰度（kurtosis）：Leptokurtic、platykurtic
It deals with whether or not a distribution is more or less “peaked” than a normal distribution.
Kurtosis（峰度）通常是与正太分布进行对比的：
- 正太分布的峰度为 3
- 峰度比正太分布高，则为高峰（Leptokurtic）
  - 高峰肥尾
    - 前提：与正太分布的离散程度（即方差）一样
    - 高峰时，均值周边的更加集中，即离散度更小，为了保证与正太分布的离散程度一样，则尾部需要更分散，因此导致肥尾。
  - A leptokurtic return distribution has more frequent extremely large deviations from the mean than a normal distribution.
- 峰度比正太分布低，则为低峰（platykurtic）
- 概念：Excess kurtosis = Sample kurtosis - 3

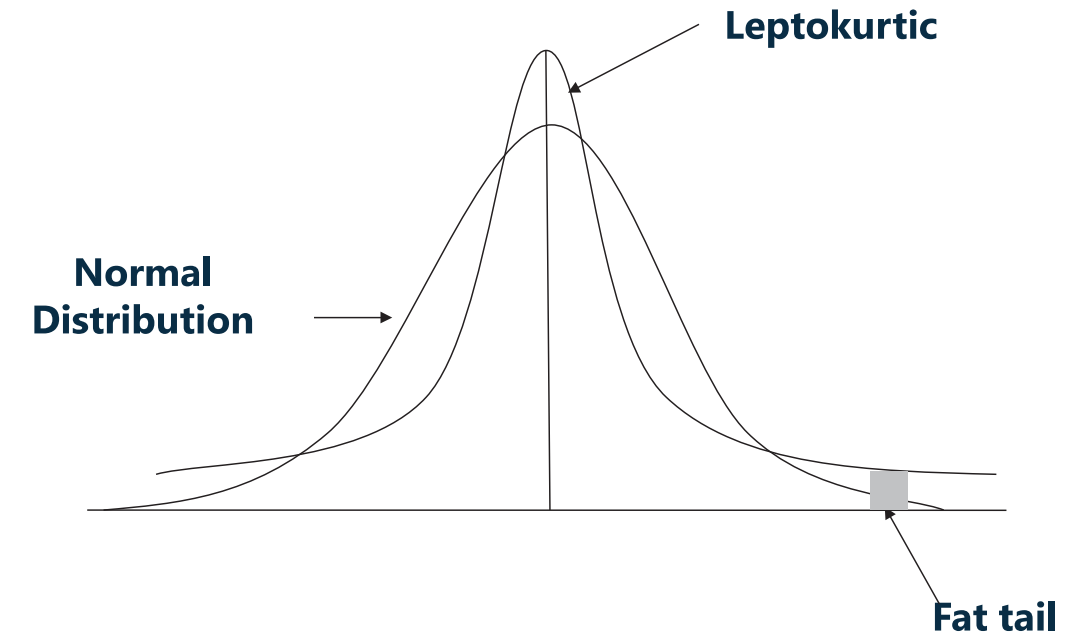
样本（Sample）峰度计算公式（不考，了解）
传统金融学中假设投资者是 risk-aversion（风险厌恶），而 risk 并不等于 loss，即风险厌恶不等于损失厌恶。风险即不确定性，高峰肥尾表明极端情况下的不确定性更大，因此投资者不喜欢。

10、例题

（1）measurement scales
只能进行排序，不能进行加减运算

（2）frequency distribution

（3）各种平均值计算

（a）HPR（几何平均）及各种平均值对比
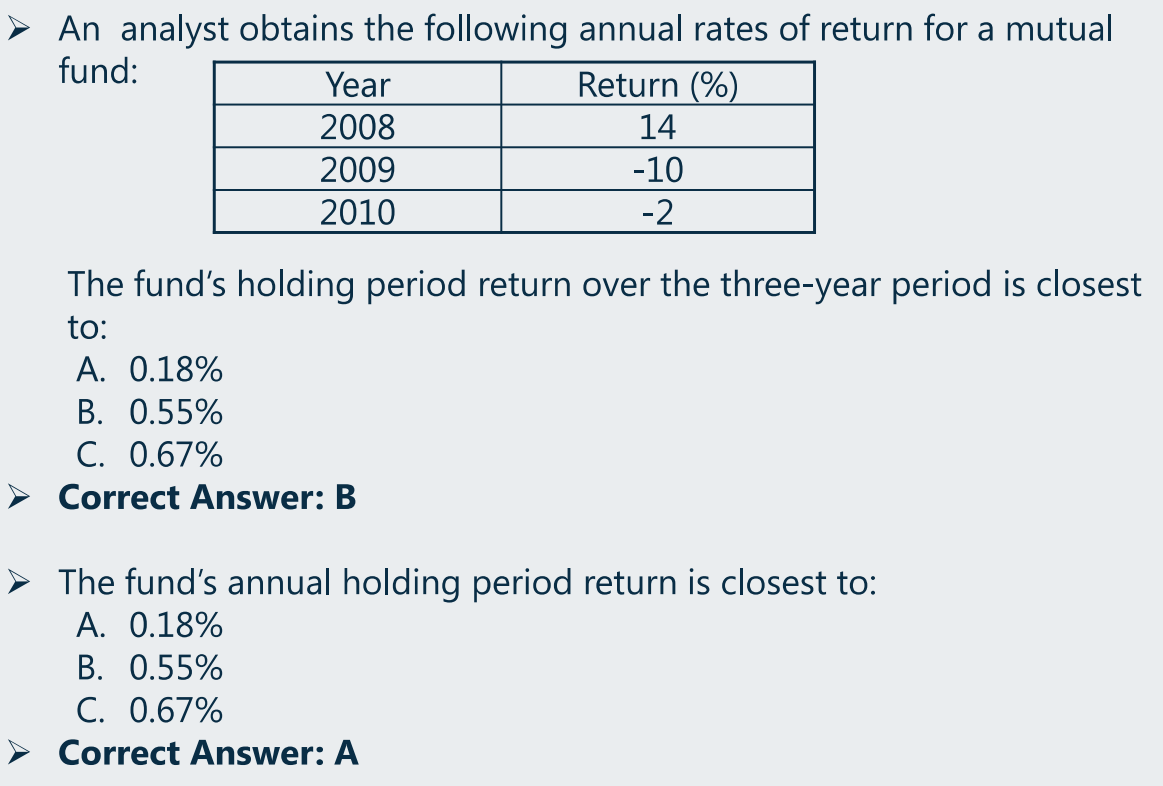
HPR 即持有这么长时间获得的 Real Return，求 Real Return 时是以复利的思想计算，即求几何平均收益率：
年化 HPR：
A >= G >= H

（b）算术平均 VS. 几何平均
确定现金流量图
先算每一期的 HPR，再算几何平均值
该题展示表明：几何平均更具实际意义（算术平均实际上很少用）

（4）Quantiles
从小到大排序，并统计总个数，通过以下公式计算目标所求数值在第几位：
- - 其中通过描述确定，如第 3 个四分位数，则为
  - 如果该值算出来是小数，则找出整数部分对应的数，以及其下一个数值，并用小数部分乘以这两个数的差值，最后将得到的结果加到整数部分对应的数上。
    （5）切比雪夫不等式
此处即