支持向量机()是在深度学习崛起之前被大家广泛研究和使用的一种分类算法。关于SVM有一句口头禅：“SVM有三宝，间隔，对偶，核技巧”
SVM的分类：
1、Hard-Margin SVM（最大间隔分类器）
2、Soft-Margin SVM
3、Kernal SVM

1硬间隔SVM-模型定义

给定一个二分类数据集，如果两类样本是线性可分的，则存在一个超平面：


那么最终得到的决策函数就是：

这里不涉及概率，是一个判别模型。
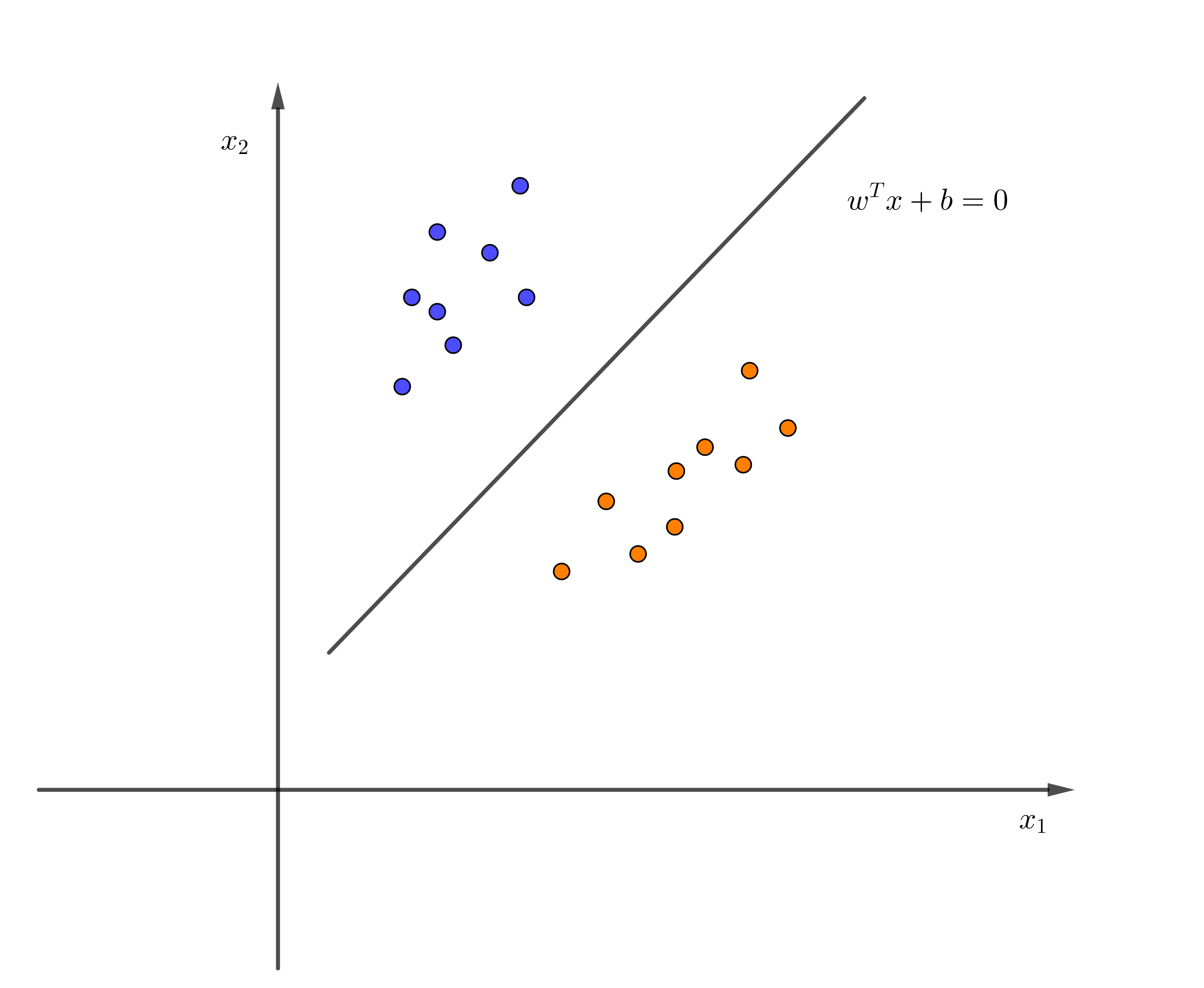
如果不同类别线性可分，那么这样的超平面就有无数个，那么哪一个才是最好的？我们希望得到的是一个鲁棒性好，泛化能力强的分类模型。
从几何意义上讲，我们希望数据离这个超平面的间隔足够大。
定义一个间隔函数，用数学语言表达“最大间隔分类器”：

样本到分割超平面的距离为：

我们定义间隔函数为最短距离：

因此，数学描述可以表示成：

与无关，因此

令，原式可写成：

进一步写成优化问题的标准形式：

这是一个二次凸优化问题，在样本维度，样本个数，维度不是很高的情况下，可以使用现成的软件求解。
为什么能直接令，这里就涉及到几何间隔和函数间隔的差别问题。

2硬间隔SVM-模型求解-引出对偶问题

如果数据量比较大，或者维度较高（采用核函数映射到高维空间中）时，计算量会非常大，无法直接求解。既然这是个带约束的二次凸优化问题，我们希望引出其对偶问题。
原问题：

既然这是个带约束优化问题，首先应写出其乘子，其拉格朗日函数为：

那么，原问题就等价于：

从逻辑上理解：
令，的集合可以分成两部分：

对于样本点，如果，
如果，
因此，，相当于在求该问题是会将不满足的空间“丢掉”
引出对偶问题：

关于对偶理论：
弱对偶关系：
强对偶关系：
由于本问题是一个凸优化问题，自然满足强对偶关系。（此处未证明）
求对偶问题，求偏导：
，将其带入得到：

,将其带入得到：

因此，对偶问题等价于：

3硬间隔SVM-模型求解-引出KKT条件

将上述对偶问题的等价形式写成求最小化问题，即：

已经求出
定理：原对偶问题满足强对偶关系满足KKT条件（此处未证明）
原问题的KKT条件包括：

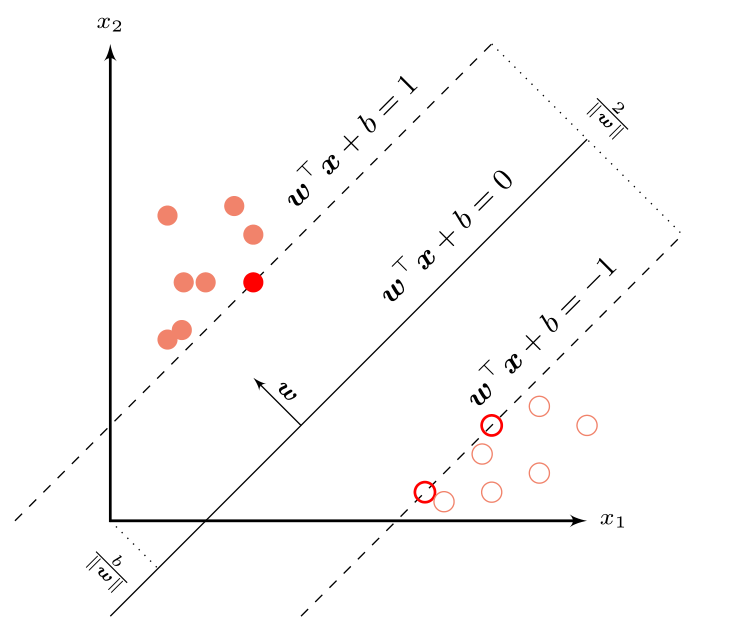
支持向量的含义：
根据 KKT 条件中的互补松弛条件， 最优解满足。如果样本不在约束边界上，，其约束失效；如果样本
在约束边界上，。这些在约束边界上的样本点称为支持向量（Support Vector），即离决策平面距离最近的点。如图所示：

已知存在样本点在约束边界上，满足，求出：

我们重新看与，由于不在约束边界上的样本以及，因此与可以看作约束边界上点的线性组合（这是支持向量的真实含义）
最终我们找到了满足“最大间隔分类器”含义的超平面，即，决策函数为：

支持向量机的决策函数只依赖于的样本点，即支持向量

4软间隔SVM-模型定义

我们回顾一下硬间隔SVM，它的前提条件就是：样本数据线性可分。因此如果样本数据无法满足线性可分条件，我们该怎么办？
再考虑另外一种情况，如果样本数据本身就具有噪声，这样的话我们得到的超平面其实是不具有鲁棒性的，这就是提出软间隔SVM的原因。
的思想就是：“允许一点点错误”，用数学语言描述就是：

我们回顾一下原问题，这是一个带约束的优化问题，硬间隔的“硬”其实就体现在它的条件约束很强，要求所有样本点都分类正确。如果我们允许分类器犯一点点错误，一个直接的想法就是不要求所有的样本都分类正确，而是要求尽可能多的样本分类正确。

因此，就可以用常见的损失函数来表示。
1、0-1损失函数

但0-1损失函数的数学性质不太好，是不连续的。因此，我们不采取这种方法。
2、hinge损失函数
考虑到距离是连续的，我们定义如果满足约束条件，我们定义；如果不满足，我们定义，将二者合并，得到：

3、指数损失函数

4、对率损失函数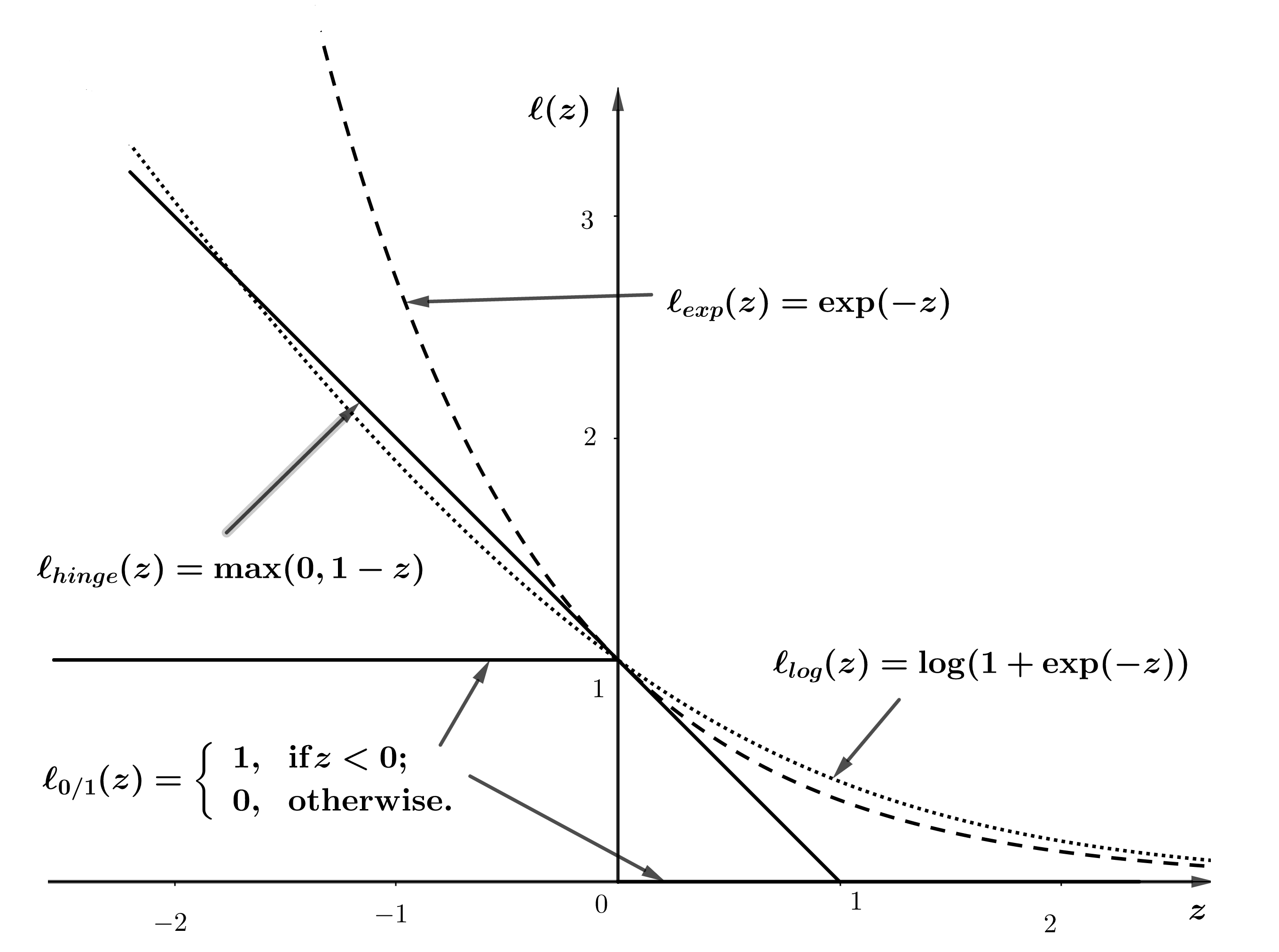


引入松弛变量，松弛因子，原问题可以记为：

5约束优化问题-弱对偶性证明

前面涉及到了优化问题的对偶关系，此处证明一下弱对偶关系。考虑一个标准形式的优化问题(原问题)：

其中，自变量，该问题的定义域为该问题的函数为：

则原问题等价于下列问题：

从逻辑上证明：
记原问题的可行域为，原优化问题也就是在中寻找一点，使得满足。
如果，即存在使得或，此时
如果，即满足原问题的所有约束条件，此时
因此，
上述等价问题的对偶问题为：

定义对偶函数：

此对偶函数的意义就是构成了原问题最优值的下界，设原问题的最优值为：即对于任意的和下式成立

证明：
对于满足，则
因此

即对于每一个可行点均满足，因此上述不等式成立。
因为不等式恒成立，因此不等式也成立，即：

这就是弱对偶性。对偶问题原问题。

6约束优化问题-对偶关系之几何解释

我们定义一个集合：

利用集合可以很容易表达优化问题的最优值

为了求以为自变量的对偶函数，我们在上极小化仿射函数

得到

假设，如果则成立，因此有：

即若对偶性成立。针对只有一个不等式约束的问题，下图描述了上述几何意义。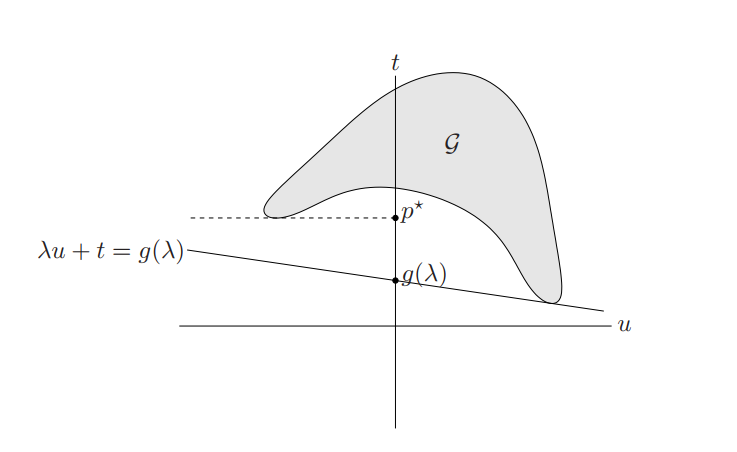

给定，在集合上极小化，得到斜率为的支撑超平面，在轴上的截距即为

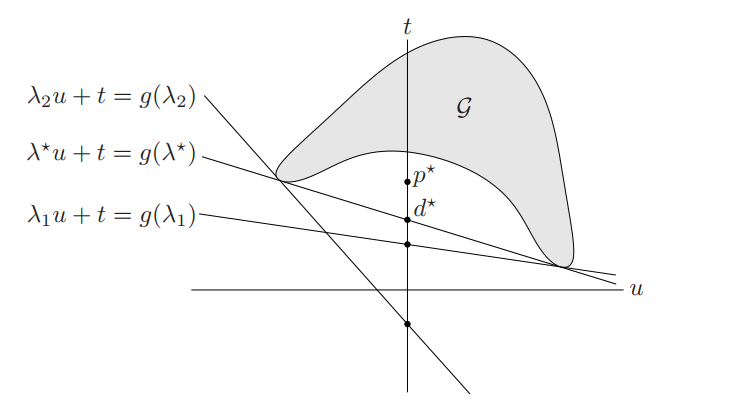
对偶可行的三个对应的支撑超平面，这三个值中包含最优值，强对偶性此时不成立

7约束优化问题-对偶关系之Slater Condition

强对偶性：
如果等式

成立，即最有对偶 间隙为0，则强对偶性成立。
一般情况下，强对偶性不成立。那么什么时候满足强对偶关系呢？如果原问题是凸问题，即可以表述为如下形式

其中，函数是凸函数，强对偶性通常是成立的（不绝对）。除了凸性条件外，还有很多强对偶性成立的条件，这些条件称为约束准则。
这里给出满足强对偶关系的一个充分不必要条件：
凸优化问题+Slater Condition满足强对偶关系
Slater Condition：
存在一点（定义域相对内部）使得下式成立

松弛的Slater Condition：
当不等式约束函数中有一些是仿射函数时，可以弱化一些条件，这里我们假设前个不等式约束函数是仿射函数，弱化的Slater条件：存在一点使得

从几何上看我们看Slater条件，也除了满足局部凸之外，还必须在的区域内至少存在一点，保证切线不是竖直的。

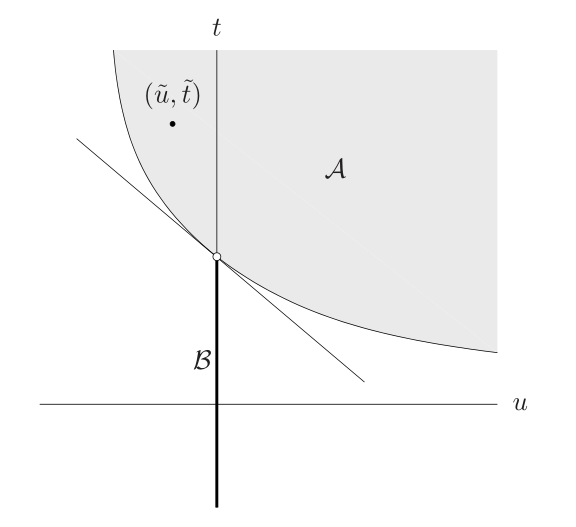
我们重新看SVM问题，这是个凸二次规划问题（目标函数是二次型函数，约束函数是仿射函数），天然满足Slater条件+凸优化问题，因此满足强对偶关系，可以使用KKT条件。

8约束优化问题-对偶关系之KKT条件

原问题为：

假设目标函数和约束条件函数均可微。
其Lagrange函数为

Lagrange对偶函数为：

对偶问题为：

又提出了一个满足强对偶关系的一个充分不必要条件：

自然满足弱对偶关系：

满足强对偶关系的条件
首先需要满足原始约束条件，即

其次，由于，因此最后一个不等号取，需满足：

第一个不等号取，需满足：

因此KKT条件为：