1背景

观察机器学习有两个视角：频率派与贝叶斯派。频率派最终发展成了统计机器学习，贝叶斯派最终发展成了概率图模型。

线性回归在统计机器学习占据基础地位，打破其特点从而发展出了各种算法，构成了统计机器学习的框架。
线性回归的特点

线性回归：

• 第一个特点是线性，包括属性线性，系数线性和全局线性。即相对于是线性的，相对于系数是线性的，相对于是线性的。

打破对的线性，如多项式回归，包含的多项式
打破对系数的线性，如神经网络，感知机。随着的不同，系数也会不同
打破对的线性，如回归，激活函数是非线性的

• 第二个特点是全局性，即特征空间是一个完整的。

打破这种全局性，如线性样条回归是在不同的空间内进行回归
决策树是对特征空间进行“纵横切割”

• 第三个特点是数据未加工，打破这个特点，如降维算法，，流形

从线性回归到线性分类
可以从激活函数和降维两个层面理解从线性回归到线性分类。

• 激活函数

，称为激活函数，在统计学中称为

• 降维

函数将从维映射到1维
线性分类的分类
线性分类大致可分为硬分类和软分类。

2感知机(Perceptron)**

样本集：，错误分类集合：，假设：样本线性可分。
模型：

**
思想：错误驱动
对于，对于正确分类的样本有：

策略：
因此，对于损失函数，一个最简单的想法是

但上式存在不连续，不可微等弱点，对于计算很不利，因此提出了下式：

损失函数对系数的偏导为：
优化算法：SGD,随机梯度下降

注意对于感知机有一个前提假设，样本集可线性可分，如果不符合该假设，有一个变体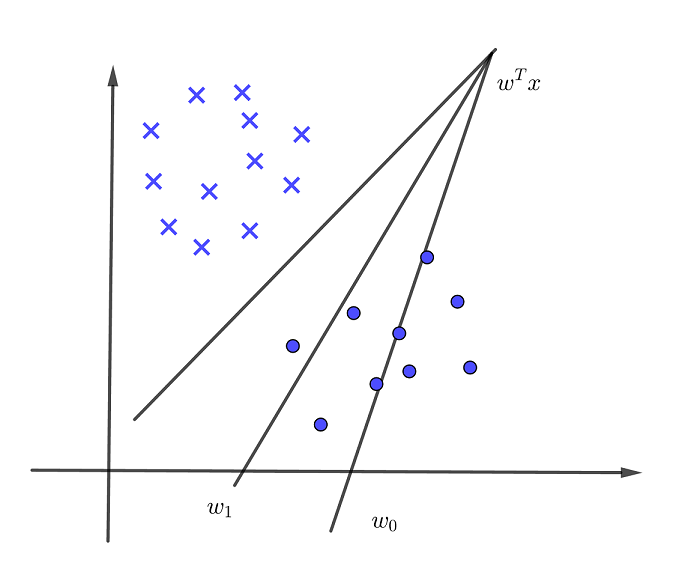

3线性判别分析(fisher)

模型定义
样本数据

思想：类内小，类间大
出发点：
借助降维地观点，希望找到一个投影方向，使得高维样本投影到某个一维方向上，使得不同的类在该方向上的投影相互分离，能够在该方向上找到一个阈值，根据该阈值能够将类识别出来。

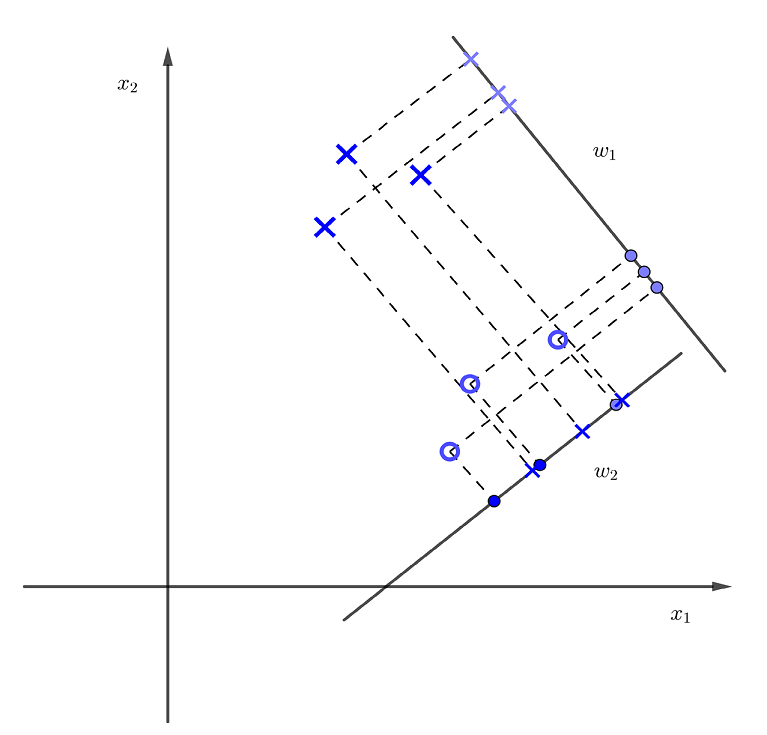
如图，很明显投影方向明显比要好。
很自然我们希望：类内小，类间大。这与计算机中的思想是一致的，松耦合，高内聚
超平面在哪？
假如我们已经找到了这样一个投影方向，那么我们要找的超平面在哪呢？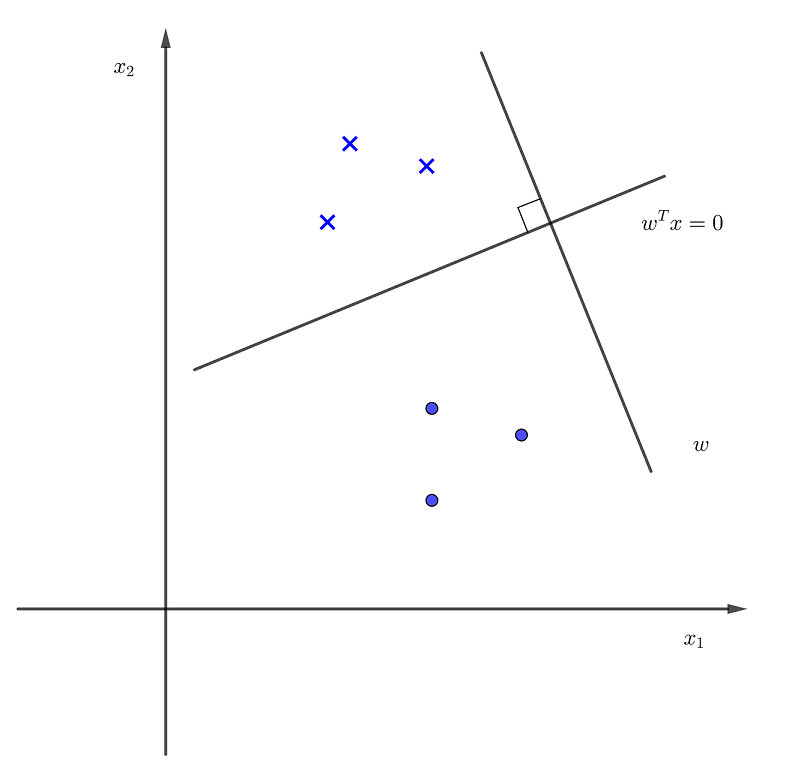

超平面与投影方向垂直，超平面为

向量垂直：

• 对于向量二者点乘可以写成代数中的向量相乘
• 若

假设上两个点为超平面向量，与垂直，则，因此超平面为

投影如何表示？
假设投影方向的二范数为1，即：
两个向量的点积：，
在上的投影为
投影
用表示在上的投影，
投影均值为：
投影协方差为：
不同类的投影均值和投影方差分别为：






类内与类间
类间距离，用度量
类内距离，用度量
目标函数


分子

分母=

所以，
因此，目标函数为

模型求解
记，类间方差；，类内方差
注意均为对称矩阵
则目标函数为：
求偏导得到

为一个实数标量，也是一个标量，因此



对于向量，有两个属性，大小和方向，我们关心的是方向，因为大小可以改变

可以看作向量在方向上的投影，是个标量。
如果是个对角矩阵，称为各向同性，则，则

4逻辑回归(Logistic Regression)

Sigmoid Function
从线性回归到，从降维的角度看，是通过一个激活函数实现，对于逻辑回归而言，激活函数就是。


函数图像：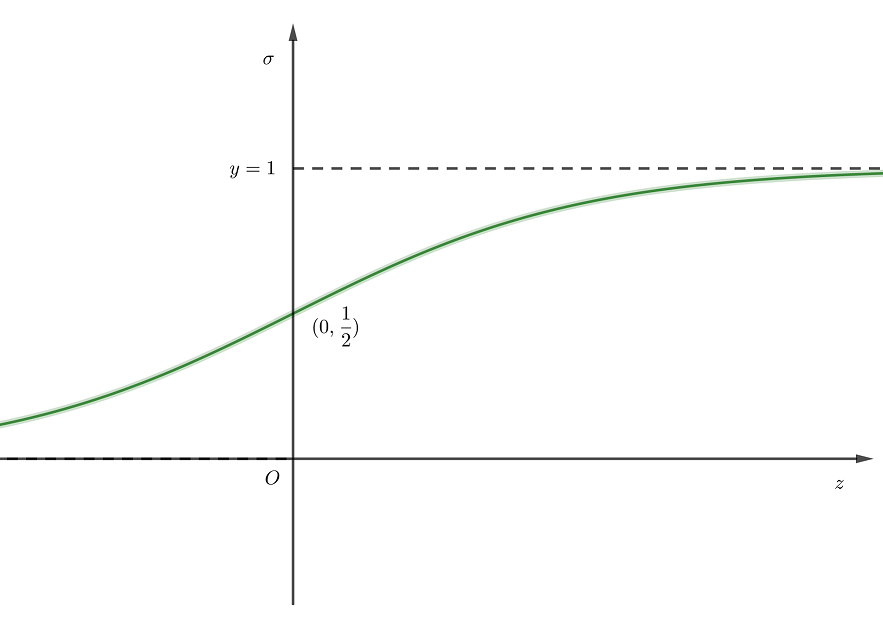



换一种更简洁的写法

从概率视角


是一种交叉熵只是前面少个。
回归采用交叉熵作为损失函数，输出标签为1的后验概率，记为，真实条件概率可以表示为

损失函数：


因此一个结论就是：

5高斯判别分析(Gaussian Discriminant Analysis)

高斯判别分析是一种生成学习算法，生成式与判别式的区别：

模型定义
样本数据

假设
一个简介表达为

假设
一个简介表达为

:

参数
设的样本个数为；的样本个数为，则
模型求解
记
求



求以为例

则

对求偏导得到


求：

记两类样本分别为，样本方差分别为


其中，
则上式可简化为



因此，上式又可写为

对求偏导得到


在该推导过程中使用到

• 
• 
• 
• 

  6朴素贝叶斯()