1极大似然估计MLE

高斯分布在统计机器学习中占据着极其重要的地位。例如：
数据集为
记，其中

极大似然估计MLE：

为了简化计算，我们假设其为一维的，即，，其概率密度函数为

对于多维的，其概率密度函数为

其对数最大似然为：

则

对求偏导得，

为无偏估计，证明：

同理，

记，对其求偏导得

为有偏估计，证明： 的无偏估计为：

小结：最大似然估计为点估计，对于高斯分布，对方差估计的结果小于真实值

2从概率密度角度观察

当随机向量维度，随机变量，是一个，其概率密度函数为

为一个二次型，一般是半正定的，这里假设其为正定的。
可以看作一个与之间的马氏距离。
当时，马氏距离 = 欧氏距离
根据对称矩阵的对角化分解：


则

令，则：


若，，从几何上这是个椭圆族。

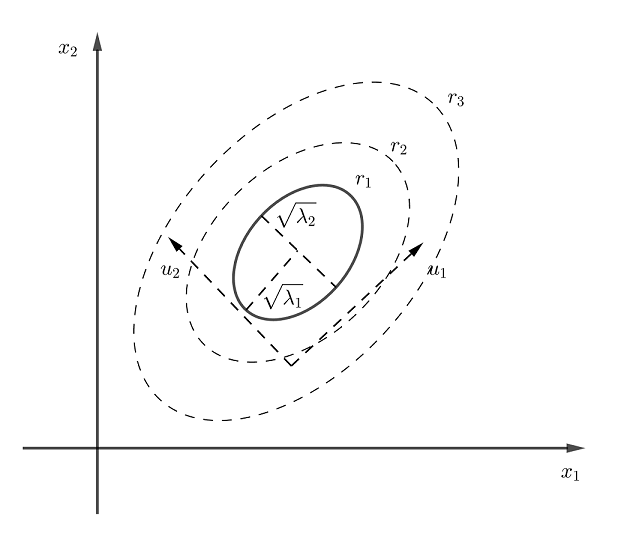
多维高斯分布的概率密度函数可以写成：

由于是一个概率值，其范围是，对于每一个值，都能找到一个，类似于一个“山峰等高线”，如图所示
**

马氏距离

引入和不同维度的尺度有关，尺度的一个度量是方差

3高斯分布的局限性

高斯分布有良好的性质，但又有一些局限性。
1、参数量过大，计算复杂
对于高斯分布，为参数，为对称矩阵，其参数个数：，这时参数过多，计算会很复杂，因此在很多时候会进行简化。

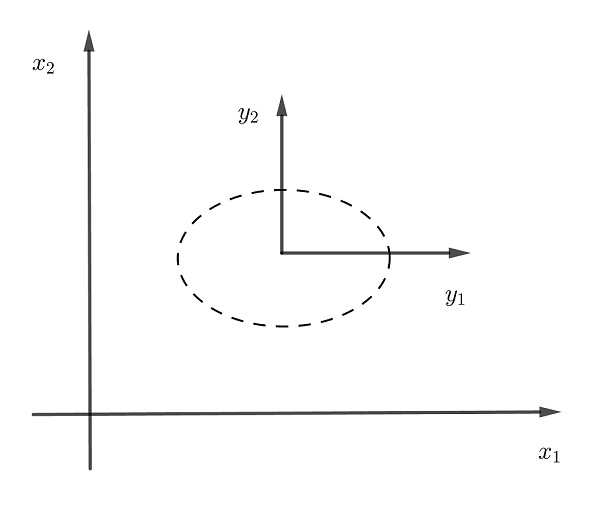
• 假设为一个对角矩阵，这时中的就是，是一个椭圆，这时的和方向相同，如图

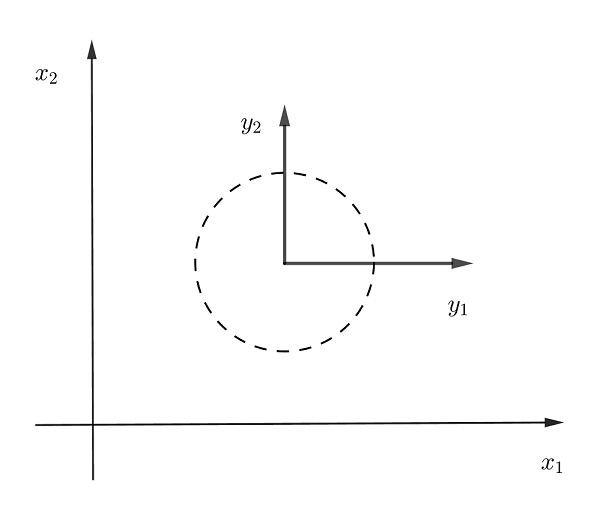
• 假设为对角矩阵，并且满足，是一个圆，称其为各向同性。如图

例如：
在因子分析中，假设隐变量()是对角矩阵
在中，假设是各向同性
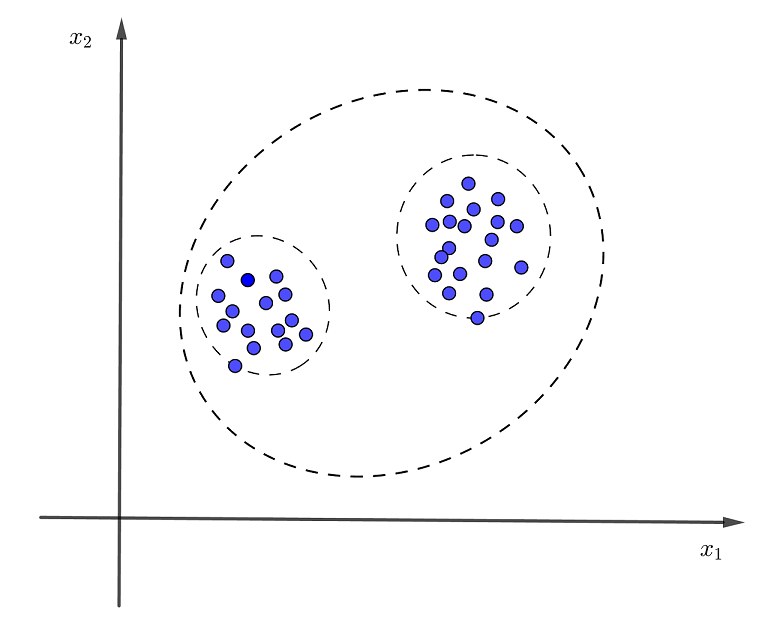
2、有时用一个高斯分布无法确切表达模型
例如，有时一个高斯分布并不能很好地表达数据，因此开发出了，如图

4已知联合概率求边缘概率和条件概率

已知：

求：边缘概率及概率概率

方法一：配方法

具体见书PRML

方式二：利用一个定理

定理：
已知，结论
注：

• 当， ，满足上述定理。
• 
• 

对于，可以想办法用表示：

根据上述结论：


因此得到第一个结论：
关于，这里提出一个构造性的证明，先进行以下定义：

由上式第一个定义，可用表示：

根据上述定理可得：


注意：
这里，求的方差时，需要满足，即与相互独立。在之后会证明。
因此，在这里



得到第二个结论：

独立性证明

上文中提到需要证明与相互独立，在这之前需要需要先证明一个结论：
若
证：
因为，所以

因为且均为高斯分布，所以
回到我们想要的证明，



所以：

https://blog.csdn.net/ResumeProject/article/details/108077468

小结

已知：

求：边缘概率及概率概率


其中，

定理：
已知，则

5已知边缘分布和条件分布求联合概率分布

已知：

求：
根据条件我们联想到贝叶斯公式：

这里有一个假设：与满足线性关系，

PartⅠ

运用上述定理：


因此，第一个结论：

PartⅡ

构造一个包含和的：

其中，

因此，可根据上述结论二，求得