1背景（概率知识补充）

顾名思义，指数族分布不是某一种分布，而是某一类分布。这类分布具有诸多优良的性质。我们常见的分布例如：Gauss分布、Bernoulli分布(->类别分布)、二项分布（->多项式分布）、Possion分布、Beta分布、Gamma分布、Dirichlet分布均是指数族分布。
指数族分布的标准形式

式中：为随机变量，为参数向量，为(配分函数取对数、配分函数在物理上有深刻的含义，这里将其理解为归一化因子)，为充分统计量。
配分函数
例：我们经常把写成如下形式：

式中，就是配分函数，我们一般将其看作归一化因子。对上式两端对取积分得到：

例如，根据贝叶斯公式可以将后验用先验和似然表示：

其中，配分函数就是一个归一化因子。
那么，上式中为什么称为配分函数？我们将指数族分布标准形式写作：

令，得到：

因此，我们将称为配分函数。
指数族分布的特点和地位
指数族具有三个特点，分别是：充分统计量、共轭和最大熵；并且在广义线性模型、概率图模型和变分推断中有很重要的地位。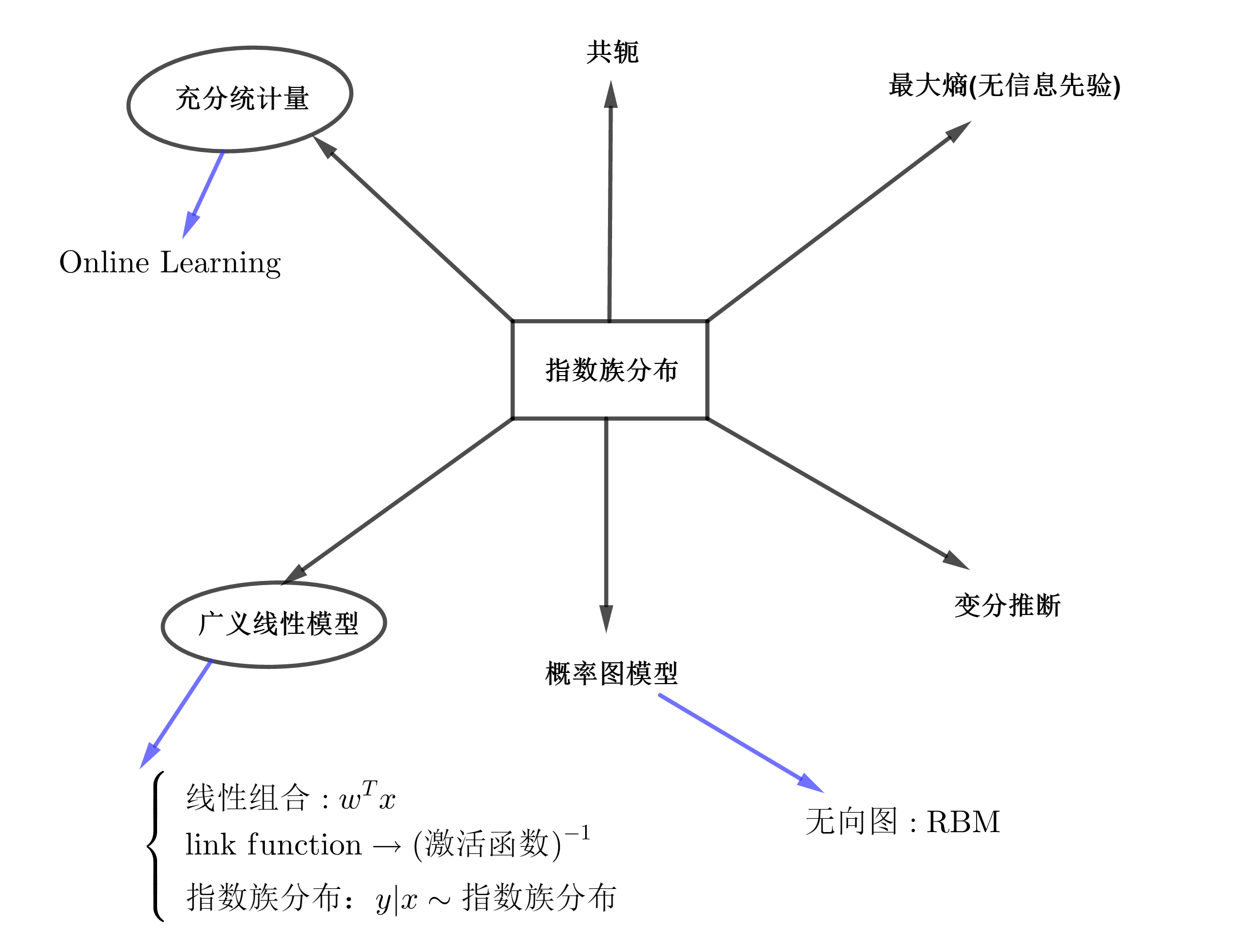

1.指数族分布的第一个特点是包含充分统计量
充分统计量的直观含义是这个统计量包含了样本中关于感兴趣问题的所有信息。
以Gauss分布为例，我们有样本，当我们有了充分统计量，我们就一个计算均值和方差，我么就可以生成一个Gauss分布，就可以扔掉样本。
充分统计量的这个优势在中就很有用，可以起到压缩数据的作用。
2.指数族分布的第二个特点是具有共轭性
我们之前提到过对于后验的求解是很困难的，困难之处在于积分困难或者我们能够获得后验的形式，但是过于复杂

因此，人们想了很多办法来解决这个问题，例如近似推断（包括：变分推断，采样推断，MCMC）。共轭是提出的另外一个求解方法。
例如，二项分布中的成功概率的共轭先验分布是beta分布，似然,先验，后验，满足共轭性的分布，在进行参数估计时，只需要关注超参数就行了，不需要关心形式。
而指数族分布天然具有共轭的优良性质。
3.指数族分布的第三个特点是具有最大熵原理的思想
我们给先验的时候可以从几个角度：1、从共轭出发，方便计算；2、从最大熵出发，（无信息先验）；3、Jerrif
最大熵原理的一个简单表述是：在满足约束条件的模型集合中选取熵最大的模型。
因此，在给参数的先验时，我们就可以从最大熵的角度出发。

2高斯分布的指数族形式

我们以一维的高斯分布为例，将它的概率密度函数改写成标准的指数族分布形式。
指数族分布的标准形式为：

一维高斯分布的概率密度函数为：

将其展开得到：

令，参数

所以，

3对数配分函数与充分统计量

指数族分布的标准形式为：

式中：
配分函数

对式子两端分别对求导，得

两端除以得到

这样就得到了第一个结论：充分统计量的期望等于对数配分函数的一次导

类似地，求二次导可以得到第二个结论：充分统计量的方差等于对数配分函数的二次导。

第三个结论是：充分统计量的协方差等于对数分配函数分别对相应的参数求偏导。

4极大似然估计与充分统计量

前面我们围绕指数族分布本身的形式进行讨论，并没有涉及到数据，现在我们假设有观测数据,我们使用极大似然估计，对参数进行估计。
根据极大似然估计，有

对参数求偏导，令其导数为0

因此，充分统计量的“充分”就体现在这，我们不需要保留整个样本，只需要记录上式右端的量就可以推断出参数。

5最大熵角度

信息量
假设我们有一个随机事件，现在我们希望能够引入一个关于概率的函数来定量描述事件包含的信息量，那么这个函数应该具备什么形式呢？
我们假设函数为，有两个独立的随机事件，其发生的概率分别是，那么这两个事件同时发生的信息量之和应该为

从概率上这两个事件同时发生的概率是，那么信息量函数就应该满足：

我们想到只有对数函数才有这样的性质，所以函数应该是一个对数函数，另外当一个事件发生的概率越大时，从直觉上会认为这个事件包含的信息量越小，考虑一个极端情况，当时，该事件是个必然事件，其信息量应该为0，所以定义定量描述信息量的函数为：

熵
我们定义熵是关于信息量的期望

最大熵等价于等可能
当我们面对未知情况时，我们自然会假设事件是等可能的发生的，当我们用定量的工具-熵对其进行描述时，发现等可能等价于最大熵。
我们以一个离散事件为例，假设其有种结果，发生的概率分别是，我们构造一个求最大熵的优化问题

写成极小化问题

其函数为

求偏导，得

所以，
所以，当我们面对未知的概率分布时，推测它为均匀分布，这个时候熵是最大的。

6最大熵模型

最大熵原理是概率模型学习的一个准则，最大熵原理认为，学习概率模型时，基于可能的分布中，熵最大的分布是最好的模型，通常用约束条件来确定概率模型的集合。所以最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
直观地，最大熵原理认为在没有更多信息的情况下，那些不确定的部分是”等可能的”。
最大熵模型的定义**
以分类模型为例，假设其是一个条件概率分布，给定训练数据集：

给定训练数据集，可以确定联合分布和边缘分布的经验分布：

其中，表示训练数据中样本出现的频数，表示训练数据中样本出现的频数。
前面提到要在满足约束条件下，选取熵最大的模型，那么约束条件如何表示呢？这里我们用特征函数进行描述输入与输出之间的某个事实。

特征函数关于经验分布的期望值，记为

特征函数关于模型与边缘分布的经验分布的期望值，记为

假设这两个期望相等，即

或

我们将上式作为模型的约束条件。
对上式的理解可以从贝叶斯公式出发，用经验分布估计条件分布：

所以有