1背景
一般机器学习更关注泛化误差,因此会尽量避免过拟合,在解决过拟合时,一般有三种方式:
- 加数据,这是最简单的方式,一些策略会有这方面的效果。例如:数据增强
- 正则化
,主要包括岭回归,lasso回归。
- 降维:直接降维即从原有特征中选择某些更有用特征;线性降维,如
;非线性降维:主要是流形学习。
对于为什么要降维,一个主要原因是维度灾难
维度灾难Curse of Dimension
随着数据维度(特征)的增加会出现三个问题:
1、特征数据的稀疏性
2、过于“重视”高维空间的噪声,导致过拟合
3、特征数据分布在高维空间中的“角落”
稀疏性
在增加维数时,样本的密度会呈指数形式下降。假设1维中长度为5个单位,2维中会有25个单位,3维则会达到125个单位,样本数目是固定的,假设是,则对于高维空间,样本密度则呈指数形式下降
。
为了获得更好的效果。也许我们增加输入维度,我们会得到一个堪称完美的分类器?其实不然,因为当特征达到一定维度后,再去增加维度会导致分类器的性能下降,这便是经常提到的“curse of dimension”如下图所示:
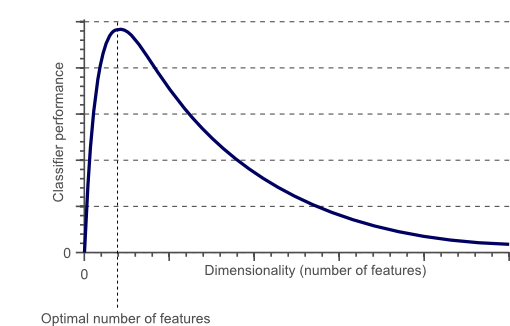
过拟合
我们以对猫狗分类为例:假定有无穷多的猫和狗,任取10个猫或狗,我们的目标是使用10个训练样例,来对无穷多的测试样例进行分类。
输入一个特征,如三原色中的红色。由图所示,单一特征几乎无法对数据进行分类,为了优化我们的模型。
输入两个特征,这次添加绿色。根据图所示,添加了第二个特征,仍然没有一条直线,可以进行线性分类
输入三个特征,如下图:三维空间中,终于能够找到一个超平面,来把猫和狗完美分类
根据这个例子,我们似乎能够归纳出一个规律:输入特征越多,便能得到更精准的分类器。正如下图的曲线所示。
3维投影到2维后的图示
高维空间,相较于低维空间,存在一个问题就是噪声误差更多,
通过上图能够看出在3维空间中线性可分的数据,投影到2维空间后变为非线性可分。
事实上,通过添加增加特征把数据映射到高维空间来获得一个优良的分类器,仅仅相当于在低维空间中使用一个复杂的非线性分类器(kernel method)。
在高维空间中,我们的分类器拟合了稀疏的训练数据,数据可能带有误差,得到的分类器缺乏泛化性。这便是由于过于“重视”高维噪声,导致过拟合。
实际上,在二维空间上的一个不那么准确的分类器,可能更优于在三维空间上的分类器。
上图在训练数据上的分类效果不如在三维空间,但这种简单的分类器泛化性能更好。即使用较少的特征,维数灾难是可以避免的,不会过度拟合训练数据。
几何上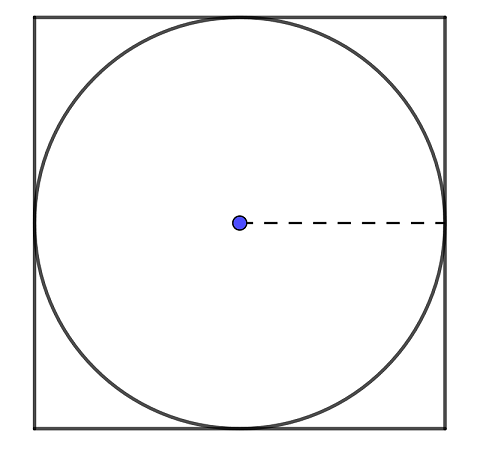
设正方形边长为1,圆半径为,若维度为
,则“圆”的体积为
即对于高维空间,特征数据分布在高维空间中的“角落”
2样本均值&样本方差矩阵
样本均值:
其中,
样本方差矩阵:
其中,
令,称为中心矩阵
中心矩阵具有以下性质:
- 对称性,即
- 等幂性,即
3PCA-最大投影方差
口诀:
对于PCA,一个口诀“一个中心,两个基本点”
目的:
一个中心:原始特征空间的重构(将一组可能线性相关的变量通过正交变换得到一组线性无关的变量)相关无关
手段:
两个基本点:最大投影方差,最小重构距离(两个角度,本质相通)
直观理解:
以二维为例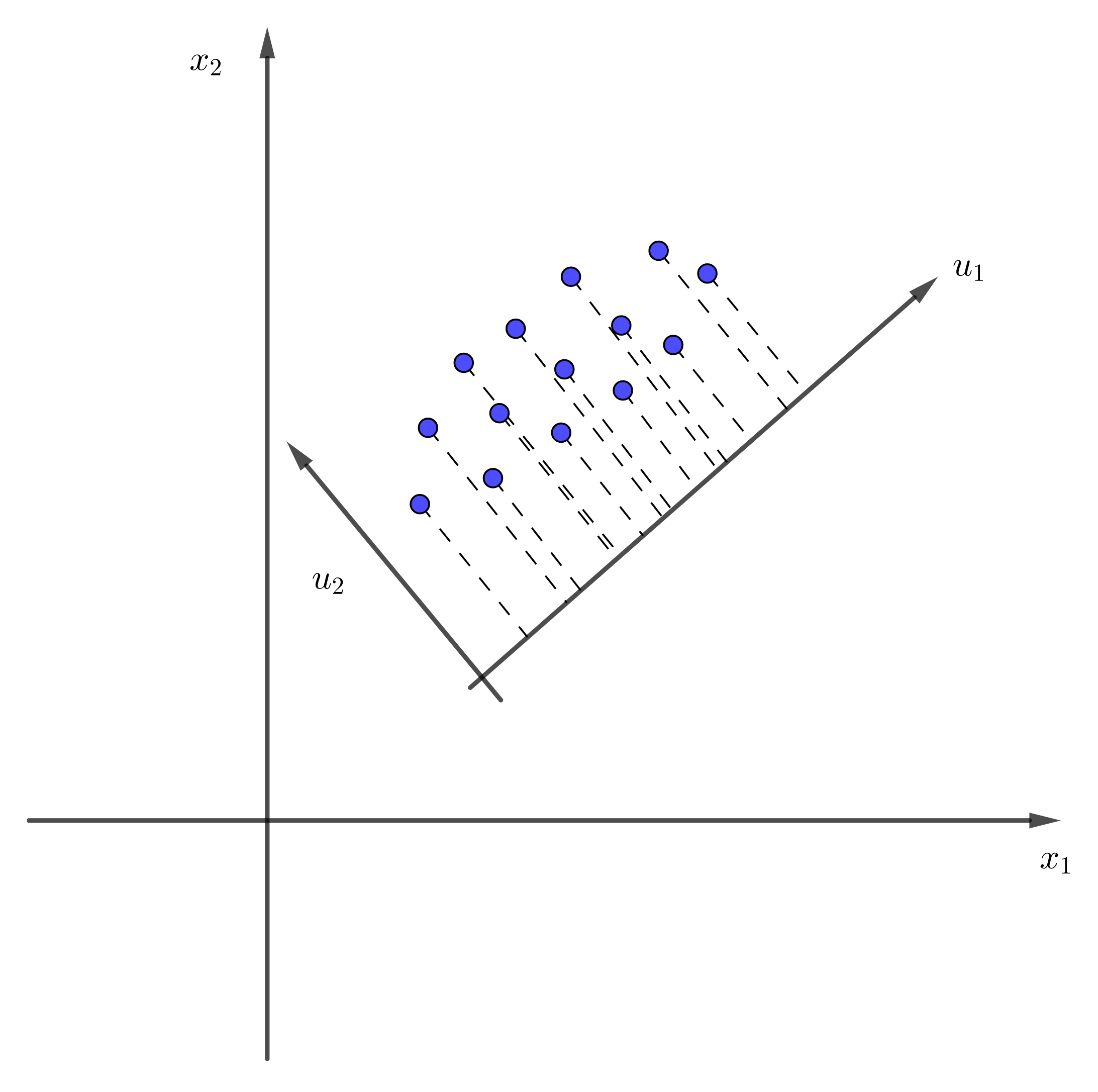
很明显,数据投影到方向,方差比投影到
方向大,重构距离(到投影方向的平均距离)比投影到
方向小。
假设就是我们要找的投影方向,则称
为主成分,我们根据需要选取
的前
个元素。
Step1:中心化
Step2:投影方差
其中,约束条件为:, 因此求投影方向
就转换成了一个带约束优化问题。
Step3:求优化问题
构造:
求偏导得:
得到:为对称矩阵
得特征值
,
为其特征向量
4PCA-最小重构距离
通过上面的推导我们发现,我们寻找的投影方向其实就是协方差矩阵的特征向量。
因此,可以看作两步:1、找到一组线性无关的投影向量
;2、根据需要挑选前
个投影方向,构成新的特征空间。
假设某个已经进行过中心化的数据为
在新的坐标系下的坐标可以表示为:
经过降维,取前个成分:
重构距离可以表示为:
由于前面我们假设是经过中心化的,因此重构距离可以表示为:
约束条件:
5SVD视角看PCA和PCoA
两个基本点
从最大投影方差角度,推出
从最小重构距离推出
从两个角度来看,二者都是在寻找最大投影方向(主成分)
结论:主成分就是方差矩阵的特征向量。
因此,在实际计算的时候只需要对方差矩阵做特征值分解就行了.
两个思路
思路1:直接对方差矩阵做特征值分解
由于为对阵矩阵,根据对阵矩阵的相似对角化定理,存在正交矩阵
,使得
其中,
思路2:对中心化样本做奇异值分解
对样本数据做中心化处理:
矩阵为中心矩阵
对中心化之后的样本做奇异值分解:
其中,均为正交矩阵,
为对角矩阵
带入样本方差,(去掉)得到:
从中心化的样本奇异值分解得到了的特征值分解
主坐标分析(PCoA)的主要思路是:1、得到方向(主成分);2、将数据在该方向上进行投影(本质上是得到样本在新的方向上的坐标)
以二维为例: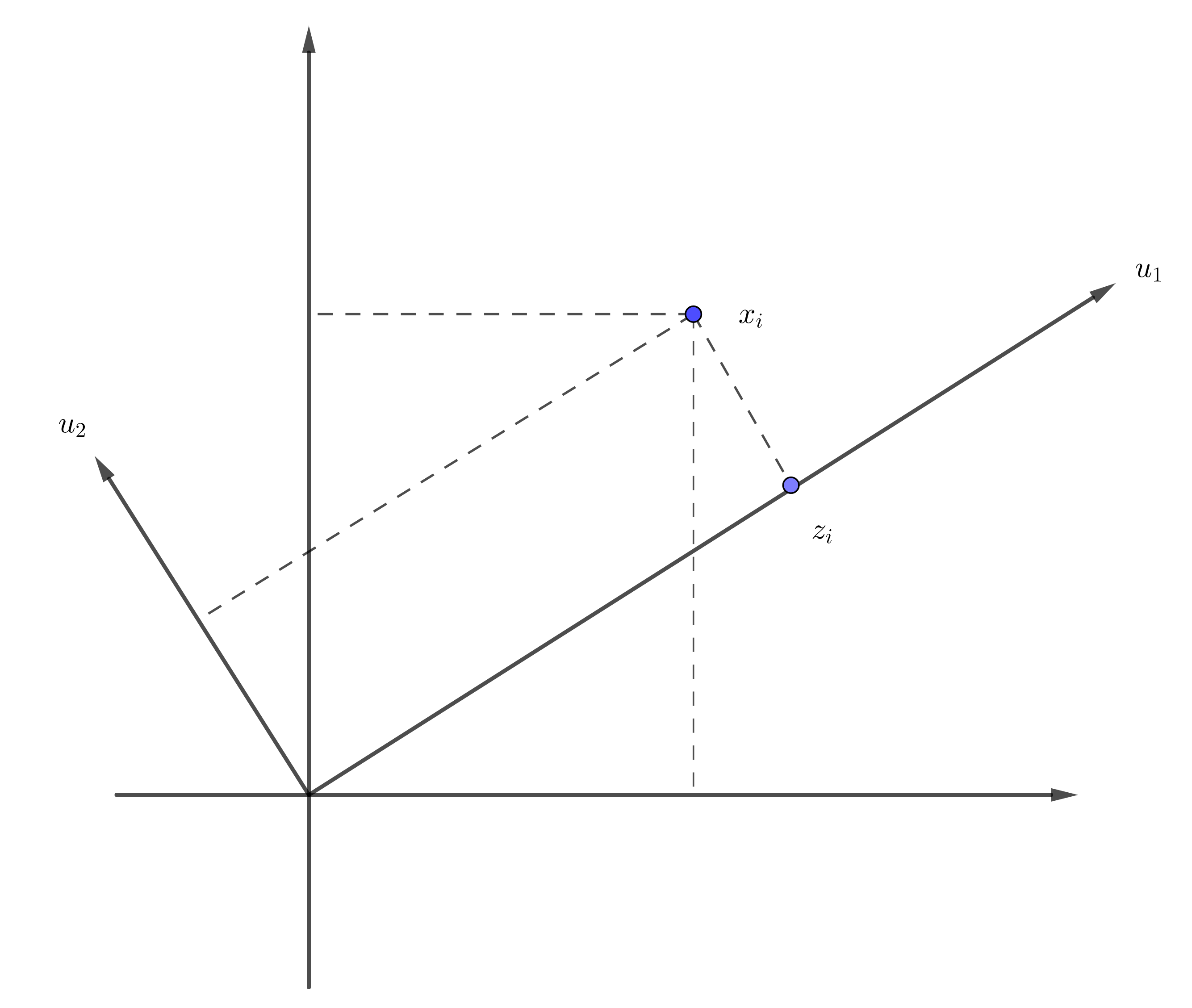
现在考虑从另一个角度出发,直接得到坐标和
具有相同的特征值
。
:特征分解:得到方向,然后得到坐标
:特征分解:直接得到坐标
为由特征向量构成的正交矩阵,
为新的坐标
为坐标矩阵
因此为
特征向量组成的矩阵
6PCA-概率角度(probablistic PCA)
回顾一下:
目的:
一个中心:原始特征空间的重构(将一组可能线性相关的变量通过正交变换得到一组线性无关的变量)相关无关
手段:
两个基本点:最大投影方差,最小重构距离(两个角度,本质相通)
目的本质上就是得到原始数据的低维表示
,
两个基本点最总都是利用原始数据集的结构信息建模一个最优化问题。
降维还可以从两个维度进行区分,1、是否线性;2、是否是生成式方法
| 降维方法 | 线性 | 非线性 |
|---|---|---|
| 生成式 | P-PCA | 变分AE |
| 非生成式 | PCA | AE |
从生成式方法的角度,认为数据集是对随机变量
的
次随机采样,随机变量
依赖于随机变量
,对
进行建模:
再对这个依赖关系进行建模:
得到的分布:
我们利用数据集对参数
进行估计
最后再使用定理求出
:
我们就可以得到每个样本点 上的
的分布
,可以选择这个分布的峰值点作为
,降维就完成了
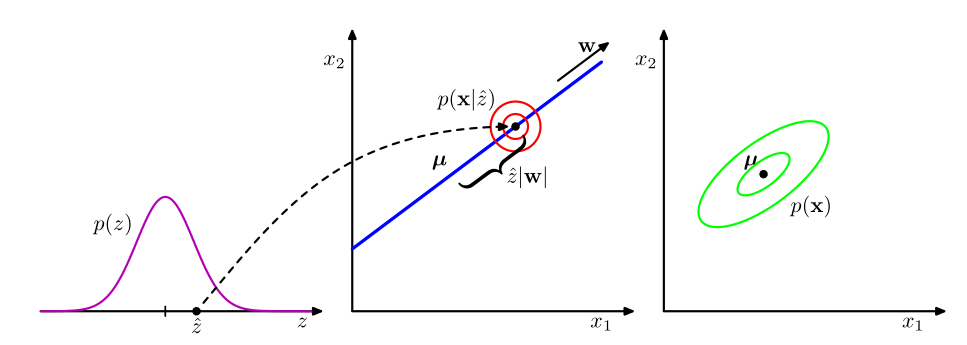
为了方便计算,我们使用线性高斯模型来计算P-PCA,
是观测数据
,
是对应于
子空间的隐变量
假设:
隐变量具有先验分布为高斯分布
,加入高斯噪声
则条件分布为:可以分成两个阶段:1、
;2、
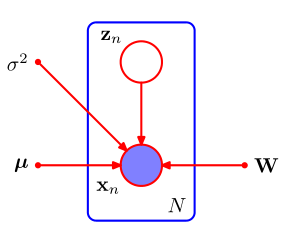
可以用有向图表示:
**

