(1)前序:
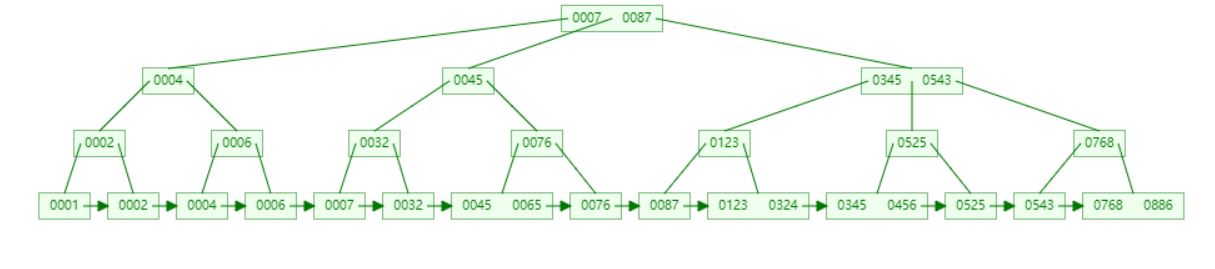
只要在一个主键索引里包含每个数据页页号与他页里的最小主键值,就可以组成一个索引目录,然后查询主键值,就可以在目录里二分查找直接定位到那条数据所属的数据页,接着数据页里二分查找定位到那条数据。
但是问题来了,表里的数据有很多很多,甚至单表几亿条数据,此时会有大量的数据页,然后主键目录里就要存储大量的数据页和最小主键值,这怎么行呢?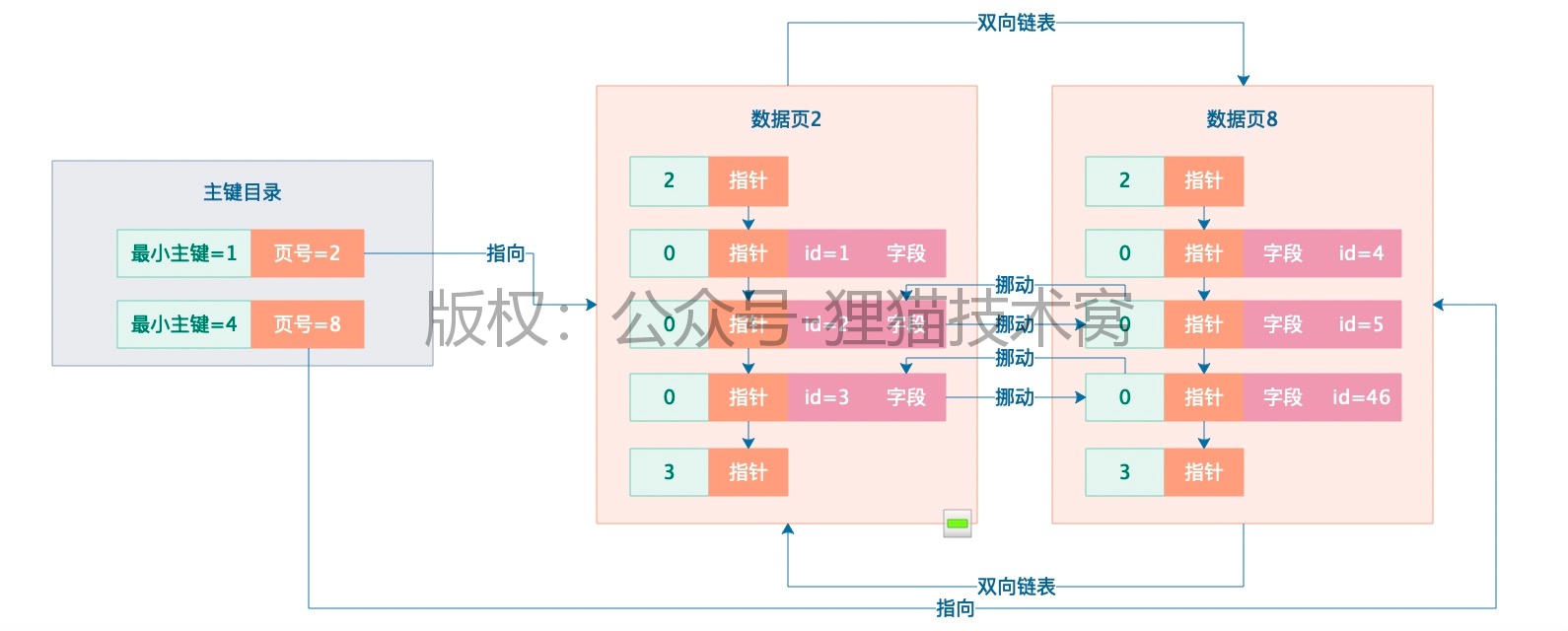
(2)数据页与索引页:
考虑上面的问题,实际上是采取了一种把索引数据存储在数据页里的方式来做的。也就是说表的实际数据是存放在数据页里,表的索引其实也是存放在页里的,此时索引放在页里之后,就会有索引页,假设有很多数据页,那么就会有很多索引页。数据页与索引页的数据结构是一样的,只是数据行类型不同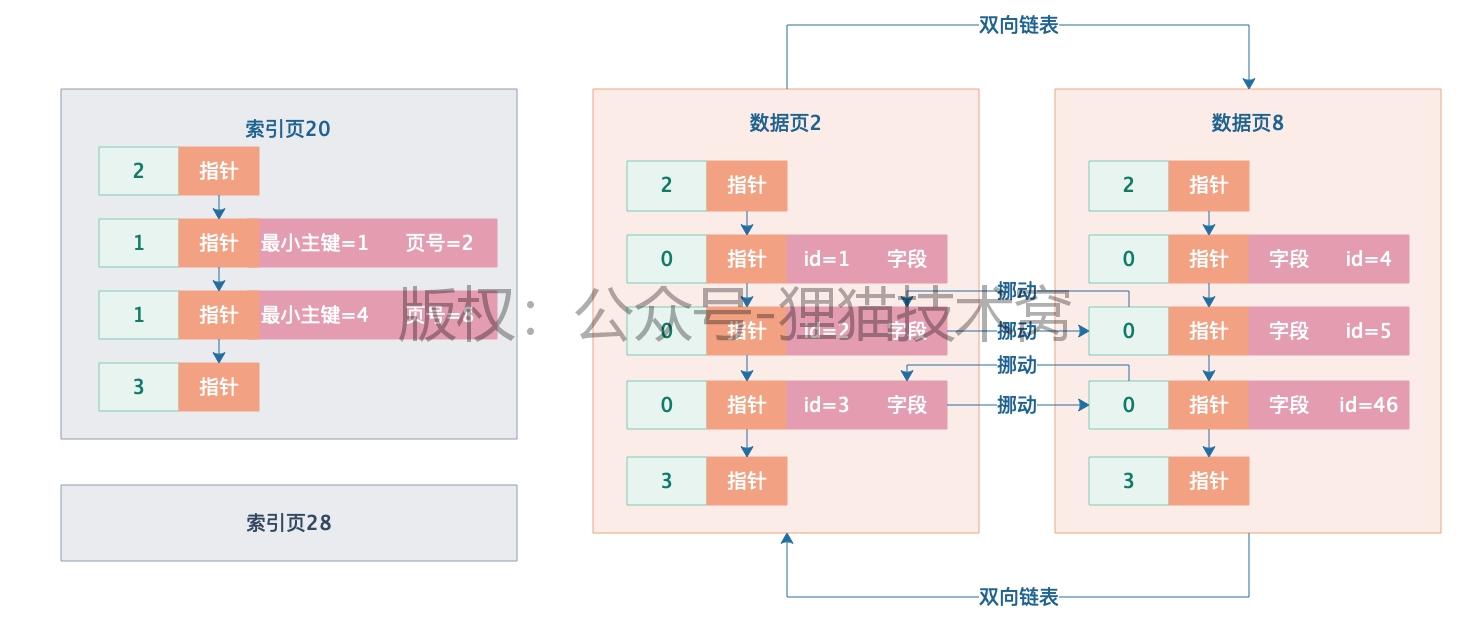
但是又会存在问题,现在有很索引页,此时需要知道应该到哪个索引页里去找你的主键数据,是索引页20,还是索引页28呢?这是一个大问题。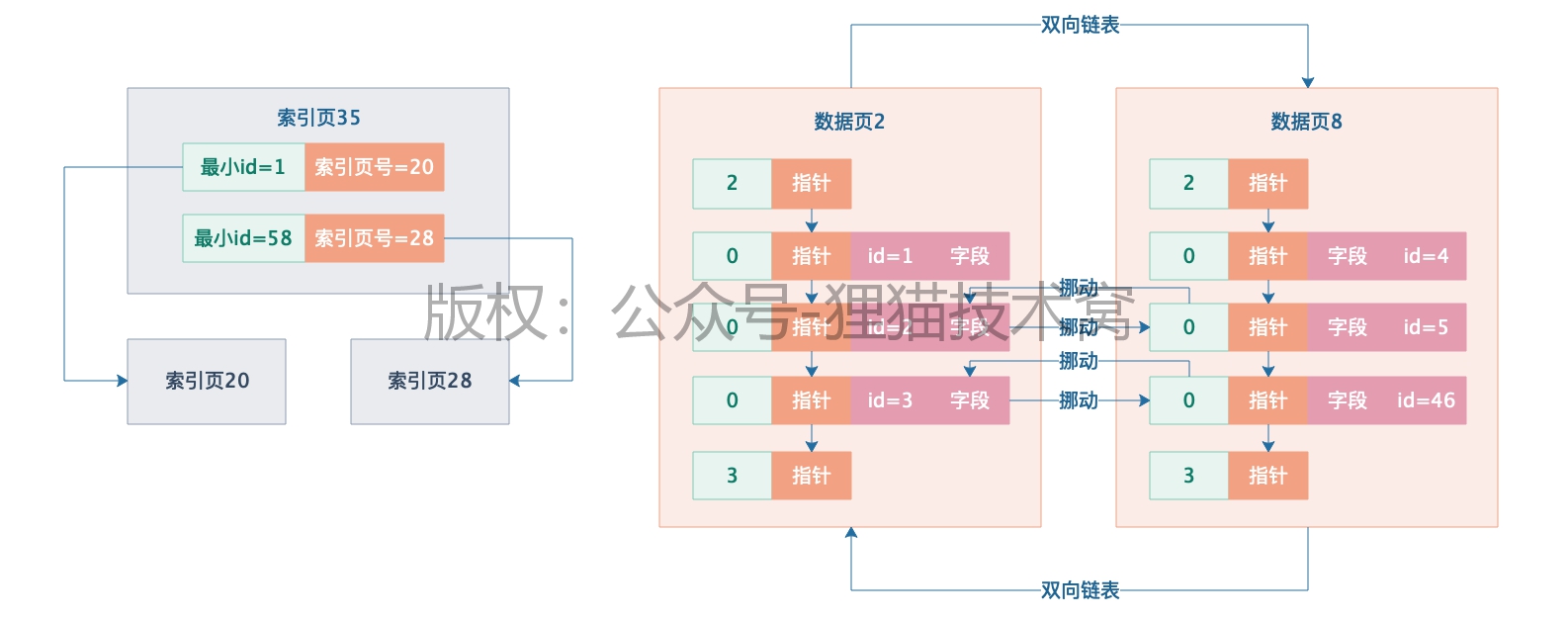
于是接下来又可以把索引页多加一个层级出来,在更高的索引层级里,保存了每个索引页和索引页里最小主键值,现在好了,假设查找id=46,直接先从最顶层的索引页35里去找,直接通过二分查找可以定位到下一步应该到索引页20里去找,接下来索引页20里通过二分查找定位也可以很快定位到数据应该在数据页8里,再进入数据页8里,就可以找到id=46的那行数据了。
现在问题又来了,假设最顶层的那个索引里存放的下层索引页的页号太多了,怎么办?<br /> 此时可以再次分裂,再加一层索引,没错了,这就形成了一颗B+树,属于数据结构里的一种树形数据结构,所以一直说**MySQL的索引是用B+树来组成的**,其实就是这个意思。我们就以最简单最基础的主键索引来举例,其实这个主键的索引就是一颗B+树,然后当要根据主键来查数据的时候,直接就是从B+树的顶层开始二分查找,一层层往下定位,直到定位到一个数据页里,在数据页内部的目录里二分查找,找到那条数据。<br /> 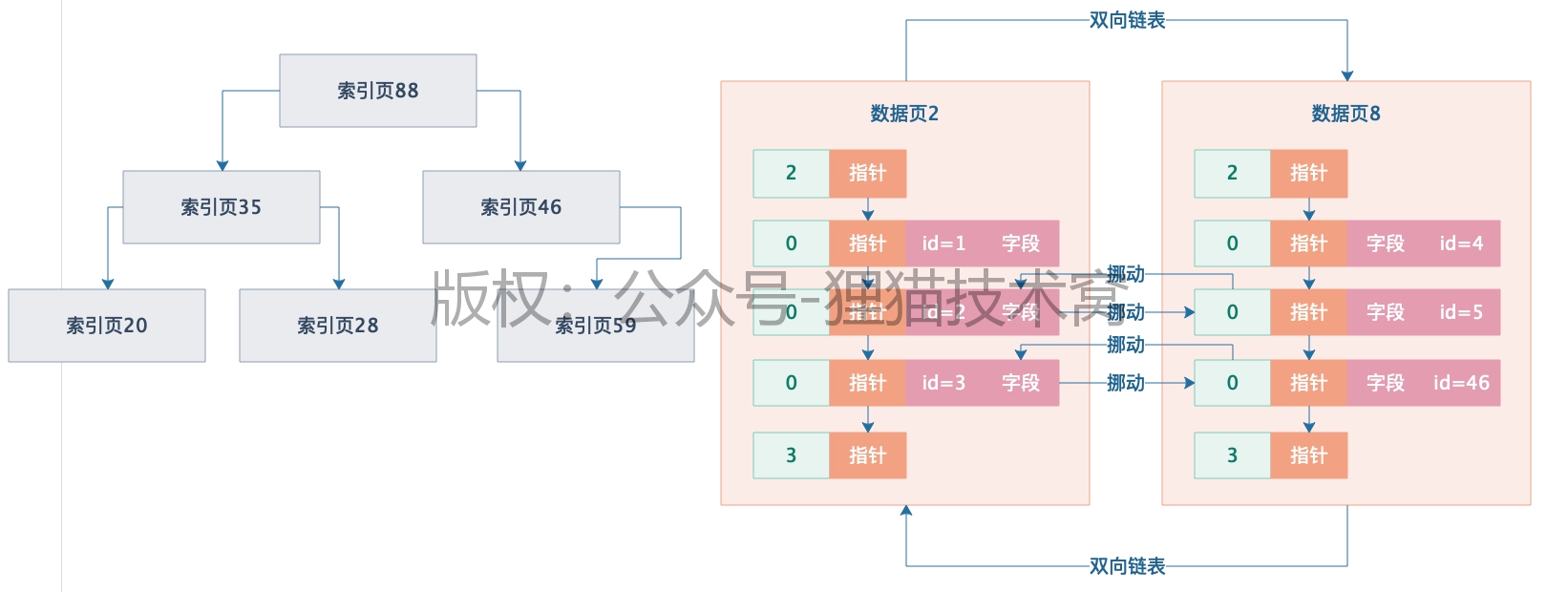<br /> <br />这就是索引最真实的物理存储结构,采用跟数据页一样的页结构来存储,一个索引就是很多页组成的一颗B+树。
问题:
如果表主键不是自增的,以自己的业务单号为主键,为了保证每个数据页的数据以主键排序,那么数据页会存在大量移动的过程嘛?索引页是以B+树存储,在树分裂的过程消耗应该没有数据页移动那么大,以自增主键和非自增主键性能差别大嘛?
解答:
性能差别很大,肯定会有大量的页分裂问题,所以一般建议是自增主键。
B+树特点:
(1)B+树 有两种类型的节点,内部节点和叶子节点。内部节点就是非叶子节点不存储数据,只存储索引,数据都存储在叶子节点,
(2)内部节点中的key都按照从小到大的顺序排列,对于内部节点中的一个key,左树中的所有key都小于它,右子树的key都大于
等于它。叶子节点中的记录也是按照key的大小排列。
(3)每个叶子节点都存在相邻子节点的指针
(4)父节点存有右孩子的第一个元素的索引。
(5)非根节点元素范围:m/2 <= k <= m-1 k 每个节点的个数,m这棵树的深度, B+树的深度最大多大,B+树的每个节点的子节点
最多多少
InnoDB 中的 B+Tree 这种特点带来的优势:
1)它是 B Tree 的变种,B Tree 能解决的问题,它都能解决。B Tree 解决的两大问题是(每个节点存储更多关键字;路数更多)
2)扫库、扫表能力更强(如果我们要对表进行全表扫描,只需要遍历叶子节点就可以了,不需要遍历整棵 B+Tree 拿到所有的数据)
3) B+Tree 的磁盘读写能力相对于 B Tree 来说更强,同数据量下磁盘I/0次数更少(根节点和枝节点不保存数据区,所以一个节点可以保存更多的关键字,一次磁盘加载的关键字更多)
4)范围查询和排序能力更强(因为叶子节点上有下一个数据区的指针,数据形成了链表)
5)效率更加稳定(B+Tree 永远是在叶子节点拿到数据,所以 IO 次数是稳定的)
B+树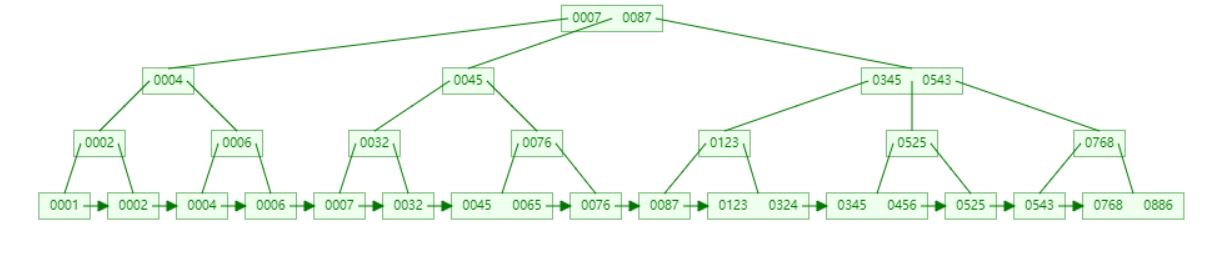
B树