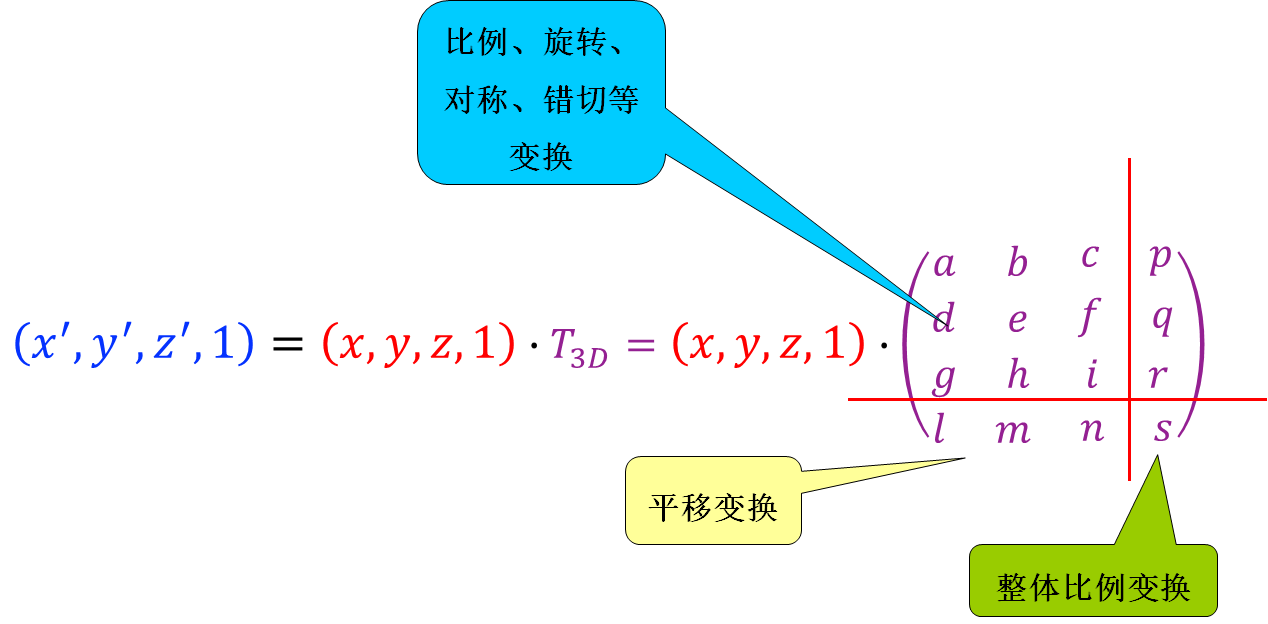
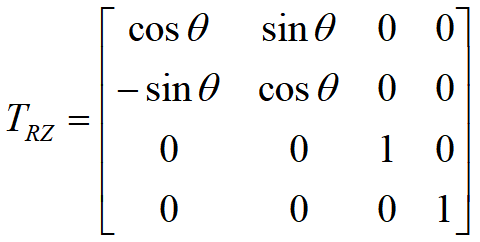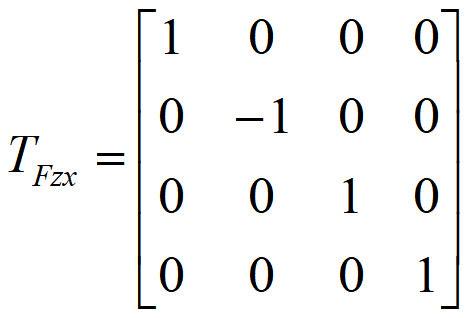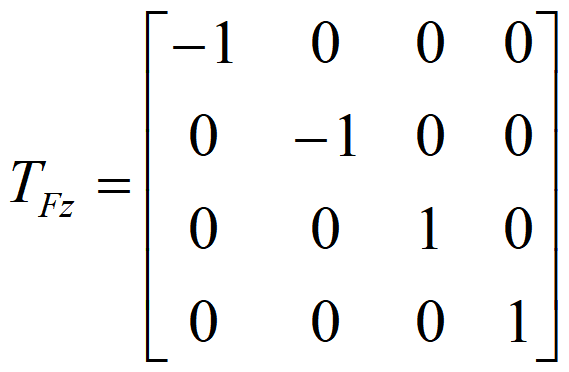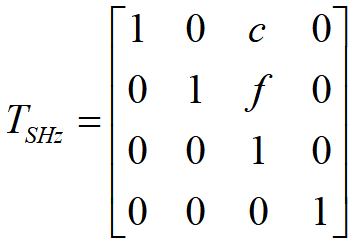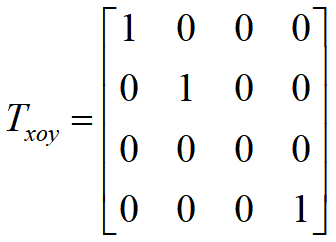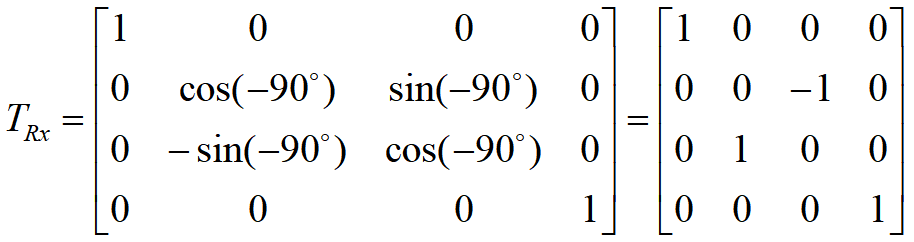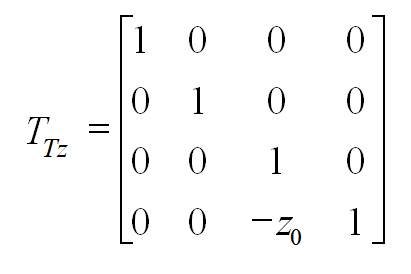三维几何变换

坐标系：
image.png
变换矩阵：
image.png

平移、比例、整体比例

从二维正常扩展到三维，无变化。

旋转

转角的正向满足右手定则：
大拇指指向旋转轴，四指的转向为正向。 即:从坐标轴的正方向观察原点,那么绕坐标轴的逆时针为正，顺时针为负。
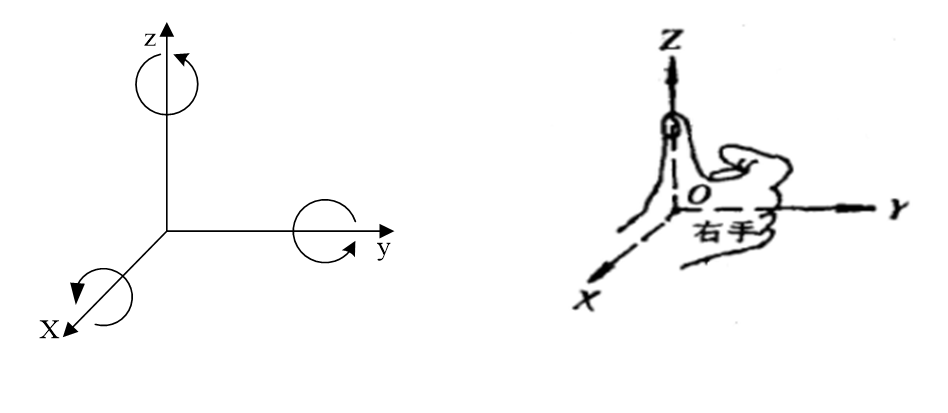
image.png
绕x、z为逆时针，绕y为顺时针。

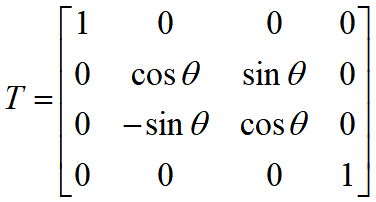
  • 绕x轴旋转image.png
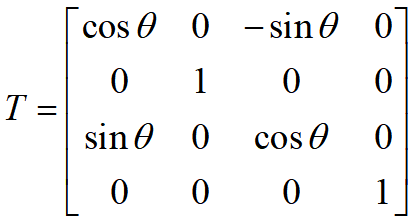
  • 绕y轴旋转image.png

  • 绕z轴旋转image.png

    对称

    关于坐标平面的对称（哪个面哪个1）

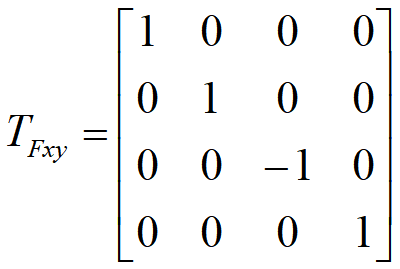
  • 关于XOY平面的对称image.png

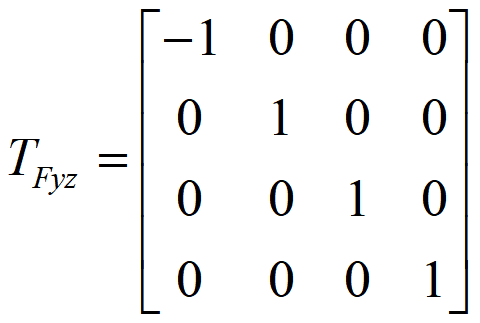
  • 关于YOZ平面的对称image.png

  • 关于XOZ平面的对称image.png

    关于坐标轴的对称（哪个轴哪个1）

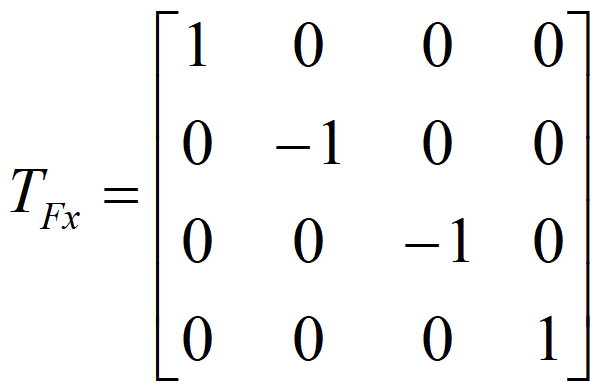
  • 关于X轴的对称变换image.png

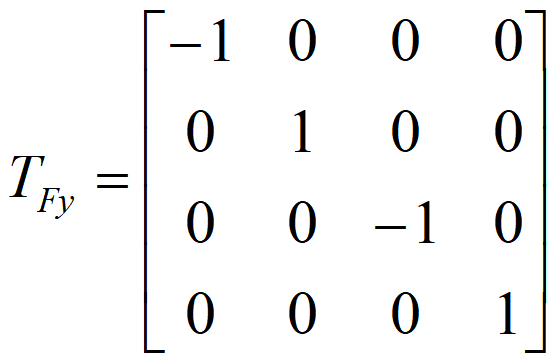
  • 关于Y轴的对称变换image.png

  • 关于Z轴的对称变换image.png

    错切

    三维错切变换中，一个坐标的变化受另外两个坐标变化的影响。

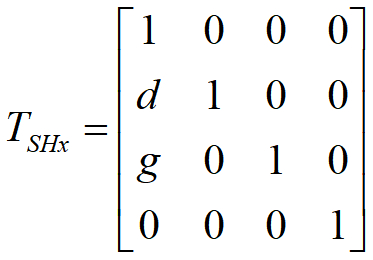
  • 沿X方向的错切第六章 三维变换 - 图13

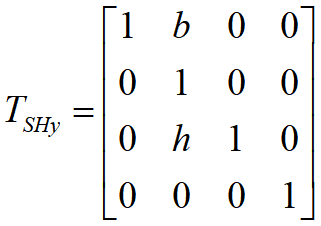
  • 沿Y方向的错切image.png

  • 沿Z方向的错切image.png

    复合变换

    矩阵相乘

    例题

    设空间线段 AB，端点为 A(0,0,0), B(10,10,10)。求空间一点 P(20,20,10)绕 AB 轴旋转 30°后的坐标。
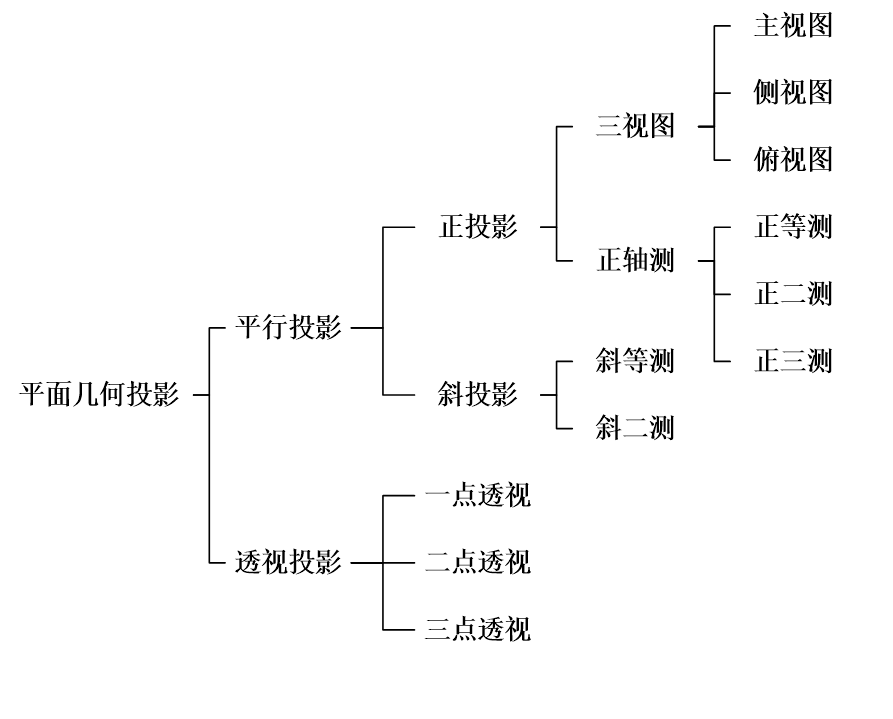
    image.png

    三维投影变换

    在三维空间中选择一个点为投影中心(或称投影参考点)，再定义一个不经过投影中心的投影面，连接投影中心与三维物体的线，称为投影线，投影线或其延长线将与投影面相交，在投影面上形成物体的像，这个像称为三维物体在二维投影面上的投影。
    投影中心相当于人的视点，投影线相当于视线。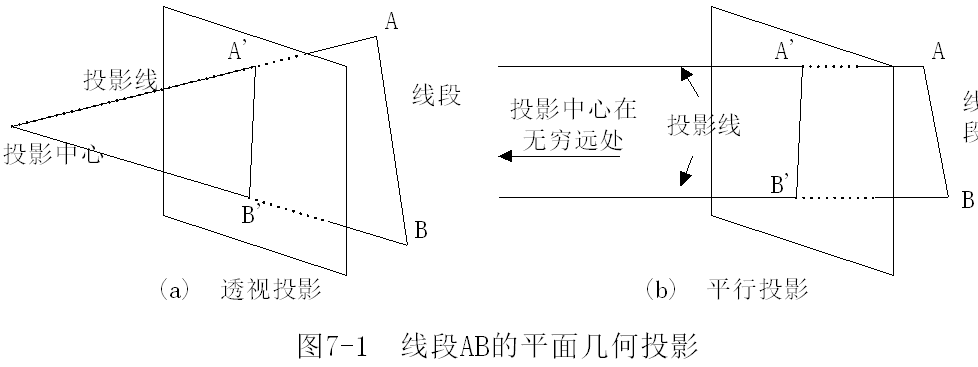
    image.png
    平面几何投影：

  • 透视投影的投影中心到投影面之间的距离是有限的；

  • 平行投影的投影中心到投影面之间的距离是无限的。

平面几何投影的分类：
image.png

平行投影

正投影

三视图

投影面与某一坐标轴垂直。

  • 主视图：将三维形体向xoz面（又称V面）作垂直投影（即正平行投影），得到主视图。第六章 三维变换 - 图19
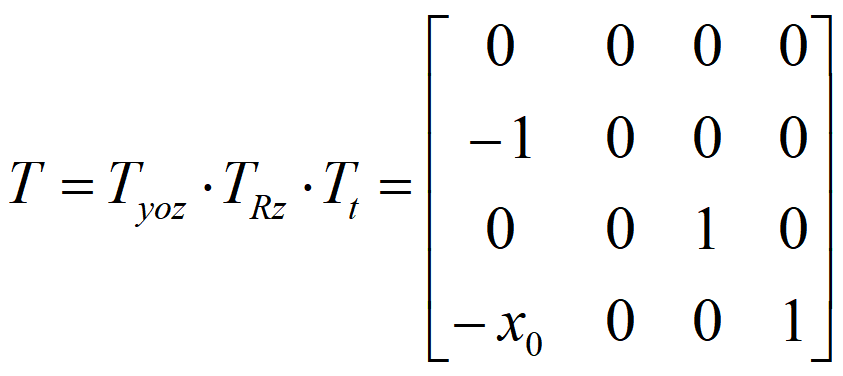
  • 侧视图：三维形体向xoy面（又称H面）作垂直投影得到俯视图。第六章 三维变换 - 图20
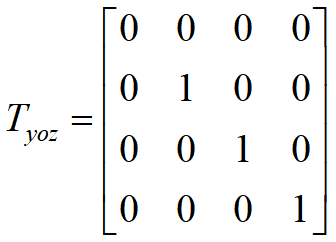
    • 投影变换image.png
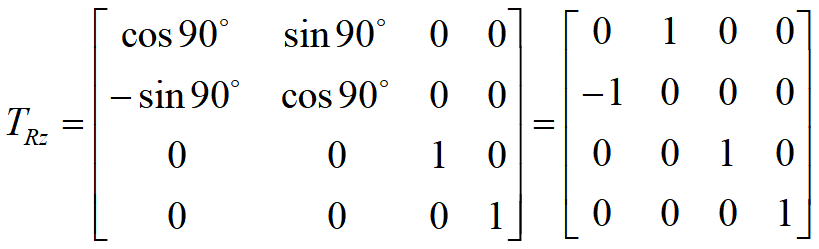
    • 使W面绕z轴正转90°，使侧视图与主视图在同一个平面上image.png
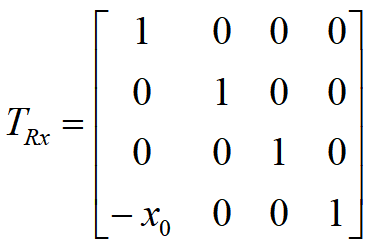
    • 使W面沿负x方向平移一段距离x0image.png
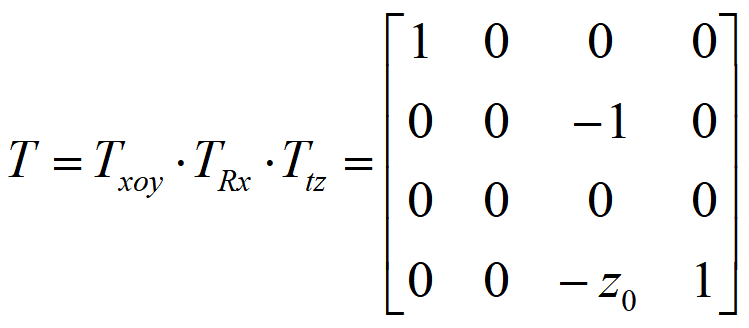
  • 俯视图：三维形体向xoy面（又称H面）作垂直投影得到俯视图。image.png
    • 投影变换image.png
    • 使H面绕x轴负转90°，使俯视图与主视图在同一个平面上image.png
    • 使H面沿z方向平移一段距离-z0。image.png

      正轴侧

      投影面与所有坐标轴不垂直。
      令：E为原点O在投影面ABC上的投影点，延长线BE与AC交于D，OF（E在OF的延长线）为投影面ABC的投影方向矢量（简称投影矢量），∠OAD=∠COD，记为α；∠EOD=∠DBO，记为β。
      正轴测投影步骤：
  1. 将OF通过旋转变换到Z轴上，使投影面ABC与XOY平行；
  2. 针对XOY面作投影。

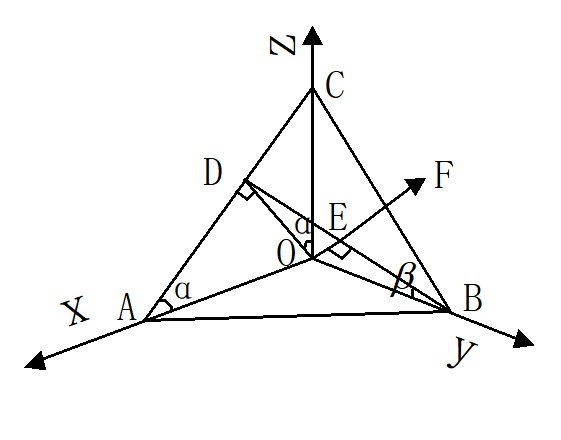
image.png
分类：

  • 正等侧：投影面与3个坐标轴之间的夹角都相等。
  • 正二侧：投影面与2个坐标轴之间的夹角都相等。
  • 正三侧：投影面与3个坐标轴之间的夹角都不相等。

投影变换矩阵：
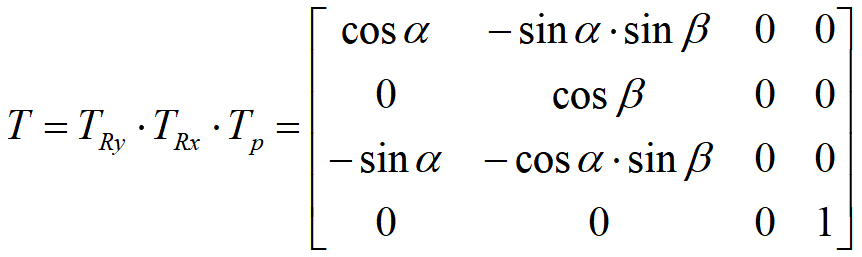
**image.png

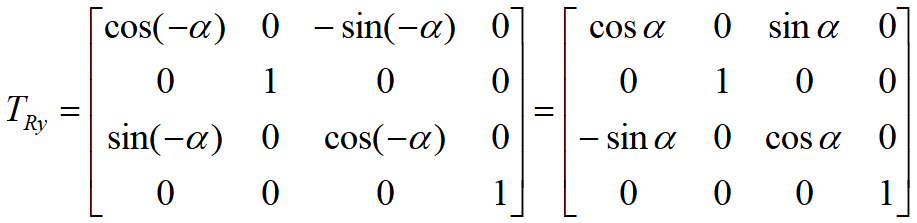
  • 先绕y轴顺时针旋转-α角image.png
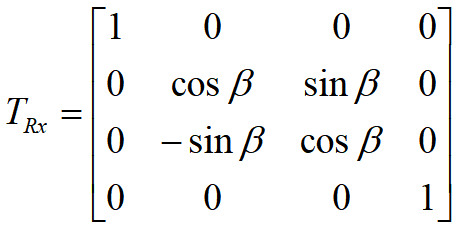
  • 再绕x轴逆时针旋转β角image.png
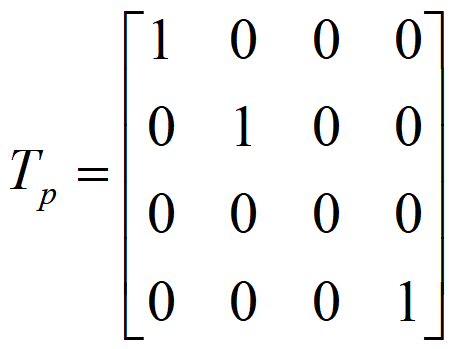
  • 将三维形体向xoy平面作正投影image.png

    斜投影

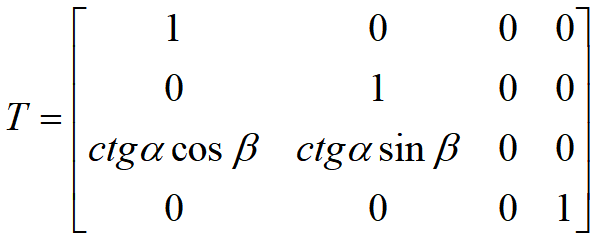
    image.png

    斜等侧

    α=45˚,ctgα=1

    斜二侧

    α=arctg(2),ctgα=1/2

    透视投影

    不平行于投影面的平行线的投影会汇聚到一个点，这个点称为灭点(Vanishing Point)。

    一点透视

    一点透视有一个主灭点，即投影面与一个坐标轴正交，与另外两个坐标轴平行。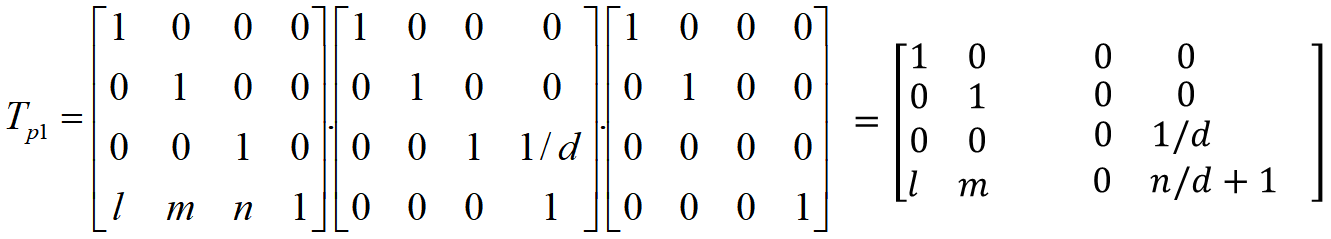
    image.png

    二点透视

    二点透视有两个主灭点，即投影面与两个坐标轴相交，与另一个坐标轴平行。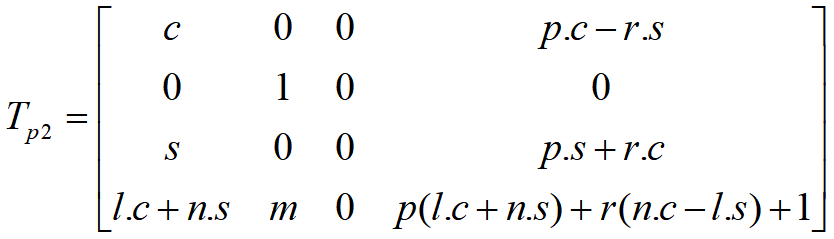
    image.pngs=sinφ,c=cosφ

    三点透视

    三点透视有三个主灭点，即投影面与三个坐标轴都相交。