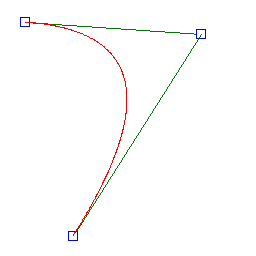
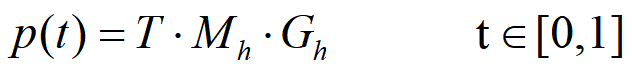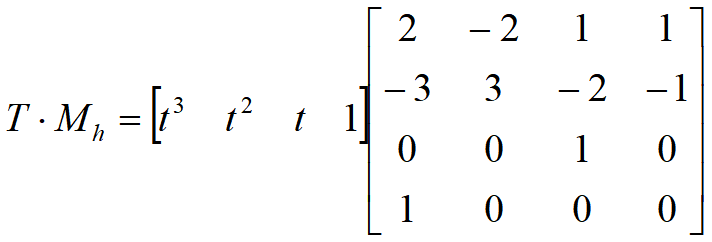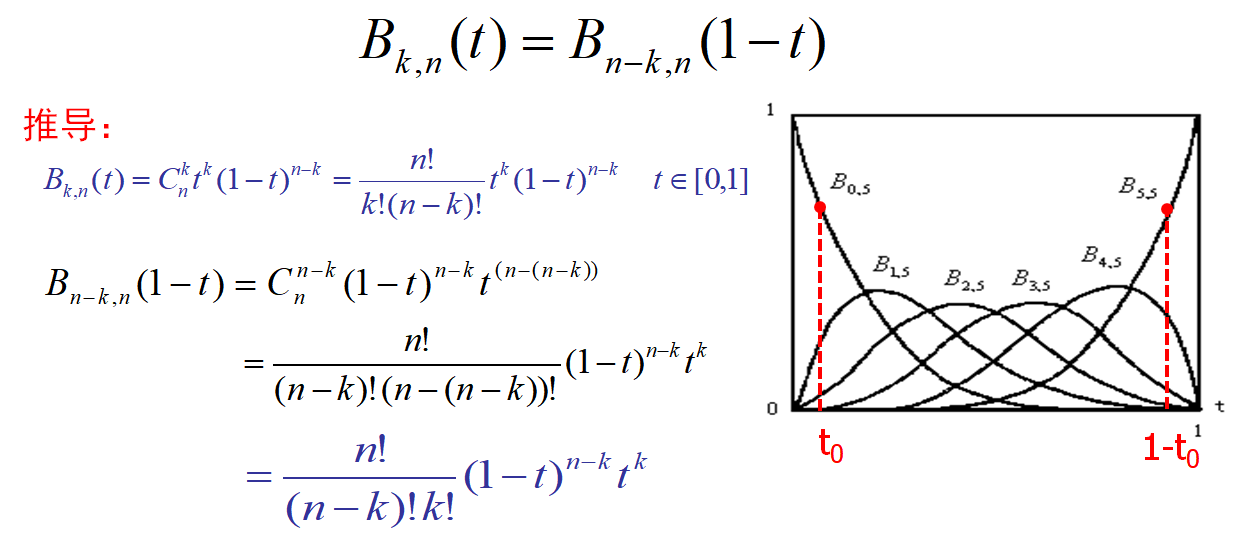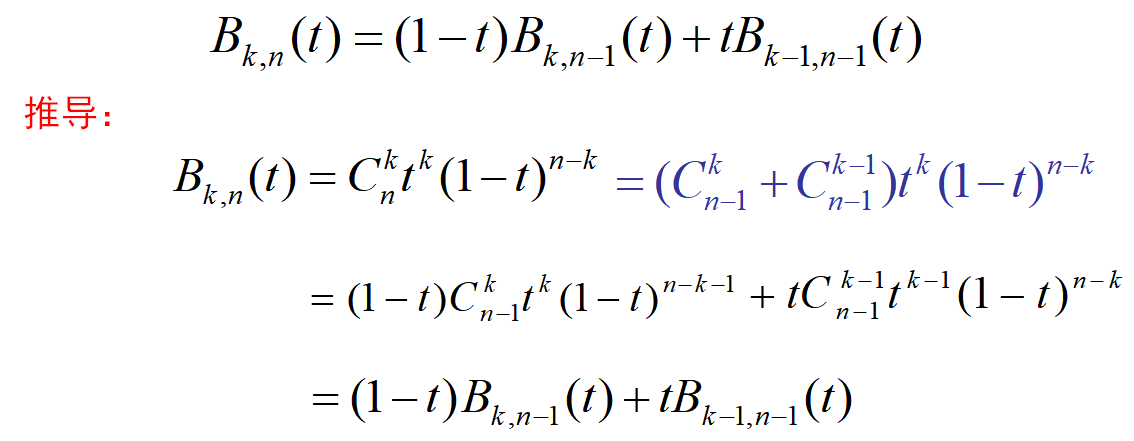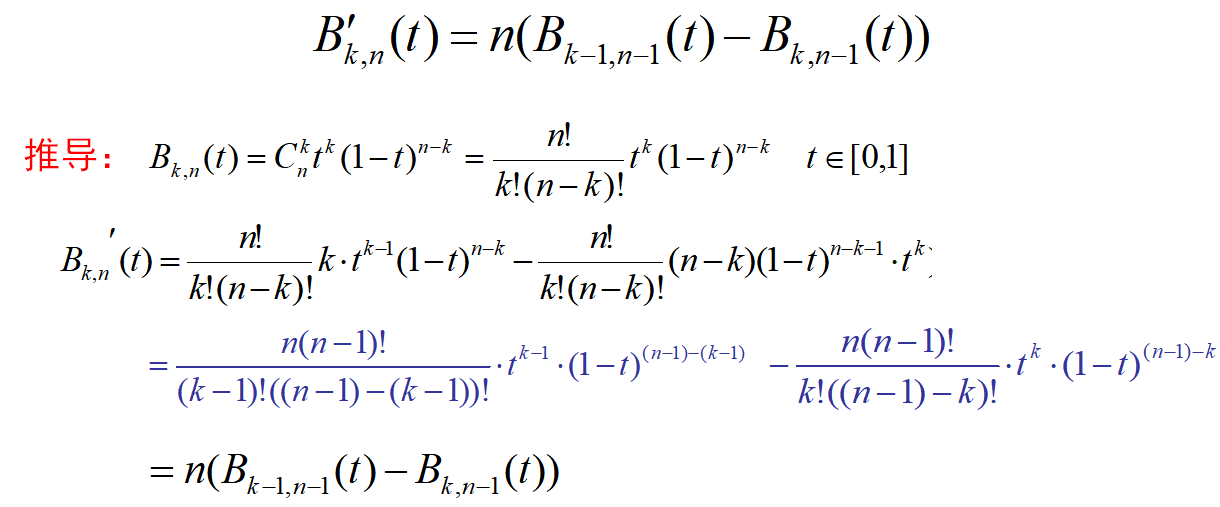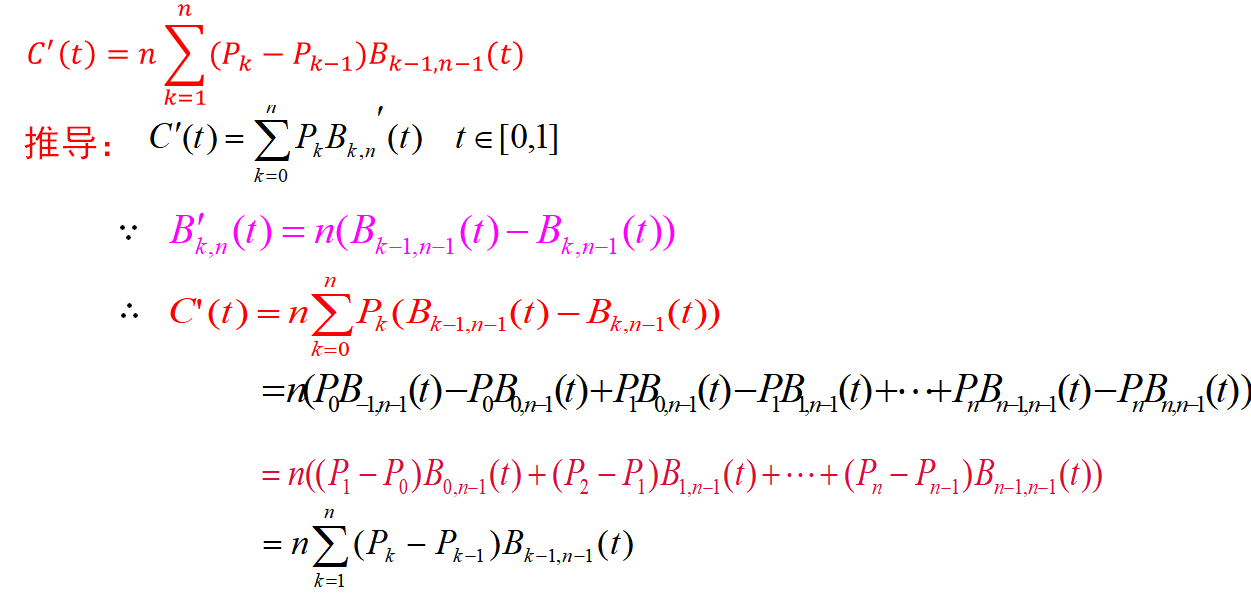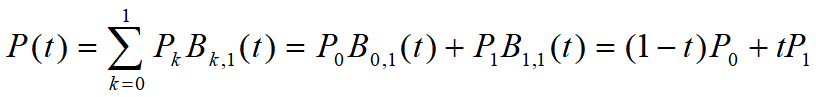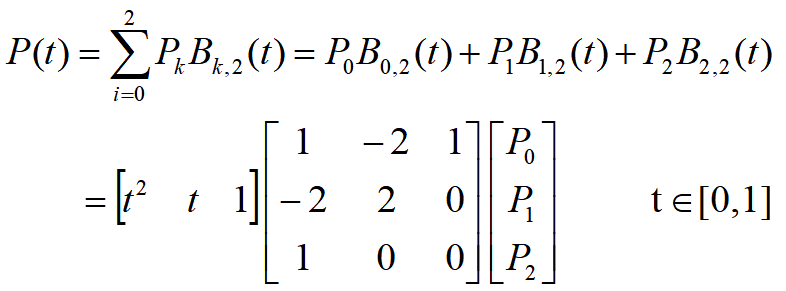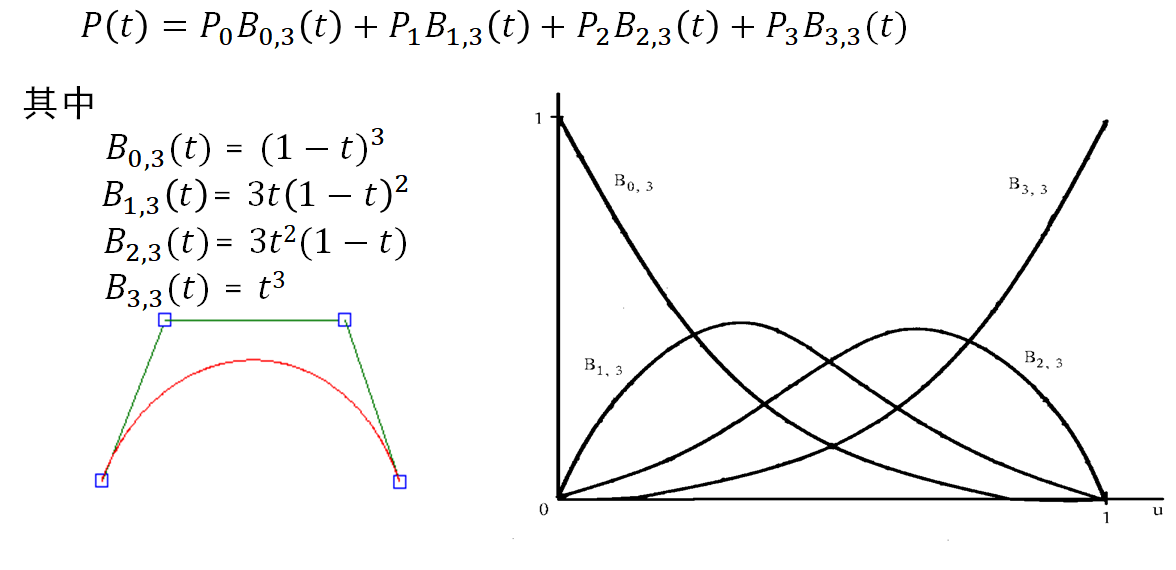曲线曲面数学描述的发展

• 弗格森双三次曲面片
• 孔斯双三次曲面片
• Bezier曲线曲面
• B样条曲线曲面
• 有理B样条方法
• 非均匀有理B样条

  曲线曲面的表示要求

1. 唯一性:由给定的有限信息决定唯一的形状。
2. 几何不变性:由给定的有限信息所确定的形状，不随所取得坐标系不同而改变。
3. 易于定界：几何形状数学描述易于定界。
4. 统一性：能统一表示各种形状及处理各种情况。
5. 易于实现光滑连接:在表达复杂形状时，经常需要将曲线段进行连接，或曲面片进行连接。
6. 几何直观：几何意义明显。

   曲线曲面的表示

• 非参数表示
  • 显式表示
  • 隐式表示

• 参数表示

  插值和逼近样条

  在自由曲线面的描述中常用的三种点：

• 控制点：用来确定曲线和曲面的位置与形状，而相应曲线和曲面不一定经过的点；

• 型值点：用来确定曲线和曲面的位置与形状，而相应曲线和曲面一定经过的点；

• 插值点：为提高曲线和曲面的输出精度，在型值点之间插入的一系列点。

  插值

  当用一组型值点来指定曲线曲面的形状时，形状完全通过给定的型值点列。
  

  逼近

  当用一组控制点来指定曲线曲面的形状时，求出的形状不必通过控制点列。
  

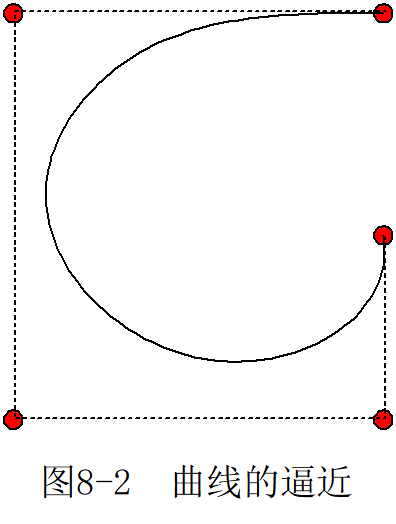
  连续性条件

  参数连续性

  如果它在t_i处n阶左右导数存在，称曲线P = P(t)在t=t_i处n阶参数连续，并且满足：
  

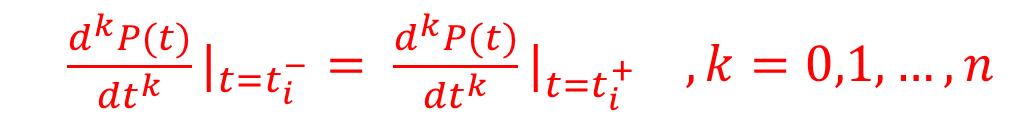
• 记号

• 若曲线在区间[0,1]内处处是连续的，则曾该曲线是连续的。

• 连续传统的、严格的连续性。

  几何连续性

• 只需限定两个曲线段在交点处的参数导数成比例，而不必完全相等。

• 记号
• 直观的、易于交互控制的连续性

注意：如果一阶导比例是a，而二阶导比例是b，a和b之间毫无关系。

样条描述

n次样条参数多项式曲线的矩阵：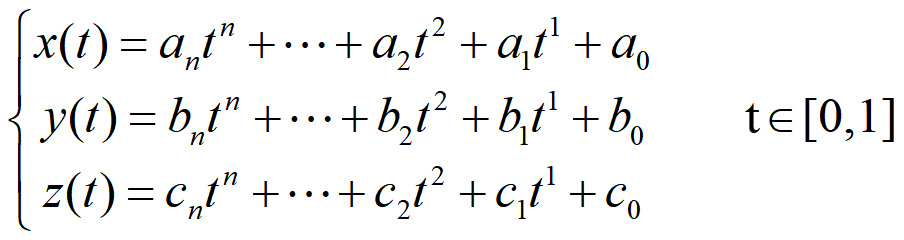

• T为n+1个幂次形式的基函数组成的矢量。
• G是包含样条形式的几何约束条件在内的矩阵，它包含了控制点的坐标值和其他已被指定的几何约束。

• MS是基矩阵，它将几何约束转化成多项式系数且提供了样条曲线的特征。

  三次样条

  
  

  Bezier曲线

  优点：

• 输入控制点与生成曲线之间的关系明确；

• 能方便地改变曲线的形状和阶次。

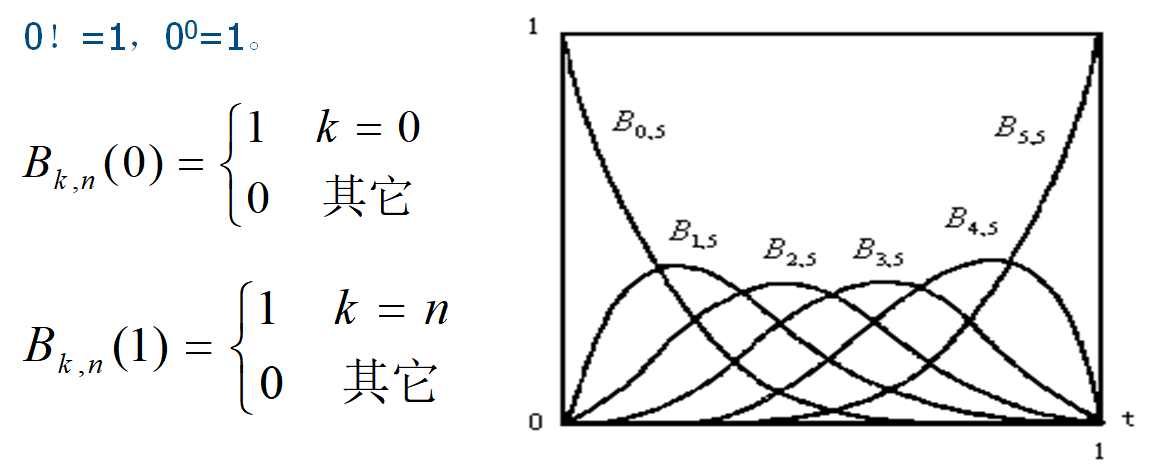
Bernstein基函数的性质

性质一：非负性

性质二： 端点的性质

性质三：对称性

性质四：权性

性质五： 递推性

性质六：导函数

Bezier曲线的性质

性质一：端点性质

曲线的起点和终点同控制多边形的起点和终点重合。

性质二：一阶导数

性质三：二阶导数

性质四：凸包性

Bezier曲线各点均落在控制多边形各顶点构成的凸包之中，这里凸包是指包含所有顶点的最小凸多边形。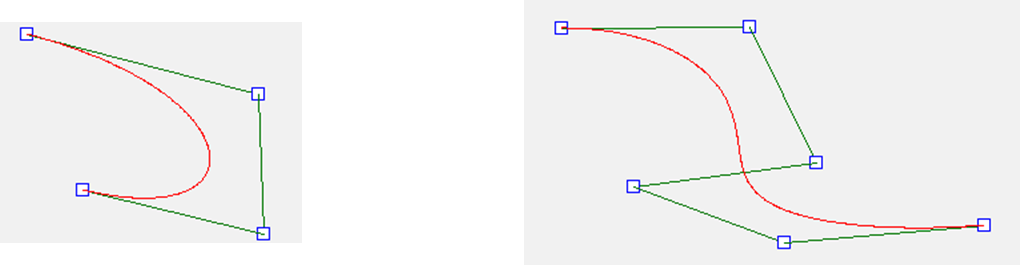

当特征多边形为凸时，Bezier曲线也是凸的；
当特征多边形有凹有凸时，其曲线的凸凹形状与之对应。
Bezier曲线的凸包性质保证了多项式曲线随控制点平稳前进而不会振荡。

性质五：变差缩减性

如果Bezier曲线的控制多边形是一平面图形，则该平面内的任意直线和Bezier曲线的交点个数不多于该直线与控制多边形的交点个数。

性质六：仿射不变性

对于任意的仿射变换A：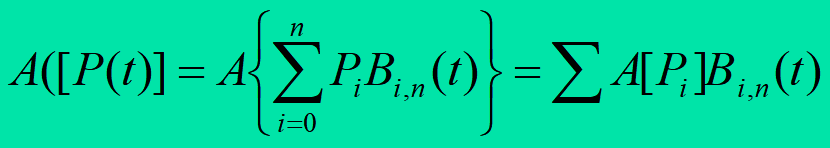

即在仿射变换下，Bezier曲线的形式不变。

性质七：几何不变性

某些几何特性不随坐标系变换而变化的特性。
Bezier曲线位置与形状与其特征多边形顶点的位置有关，它不依赖坐标系的选择。

基本的Bezier曲线

一次Bezier曲线

二次Bezier曲线

三次Bezier曲线

如何绘制一段Bezier曲线？

1. 确定曲线的阶次；

2. 计算Bernstein基函数的表达式

   

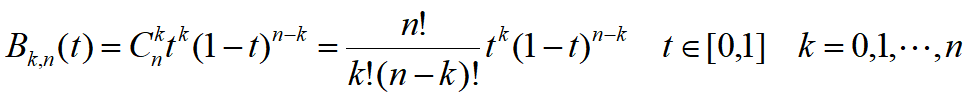
3. 把Bezier曲线中的Pk写成分量坐标的形式；

4. 确定一合适的步长；控制t从0到1变化，求出一系列(x,y)坐标点； 将其用小线段顺序连接起来。

   例题

设在平面上给定的7个控制点坐标分别为:A（100,300）,B（120,200）, C（220,200）,D（270,100）,E（370,100）,F（420,200）,G（420,300）。画出其曲线。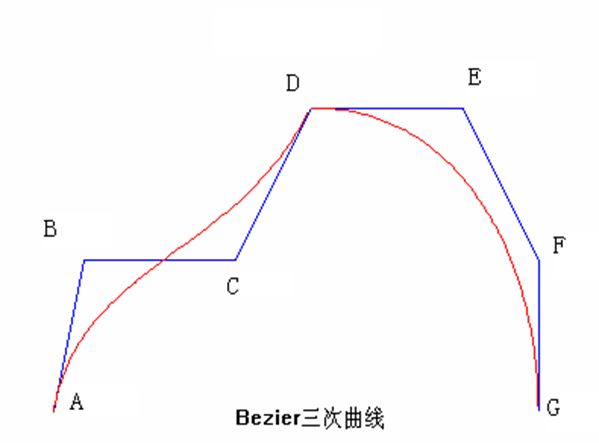

例子：设有两段三次Bezier曲线，其中一段曲线由控制点P0、P1、P2、P3生成，另一条曲线由控制点Q0、Q1、Q2、Q3生成，P3(Q0)是两段曲线的公共控制点。如果两段曲线要达到光滑连接，需要一阶导数连续，甚至二阶导数连续。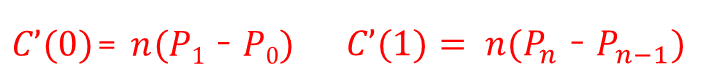

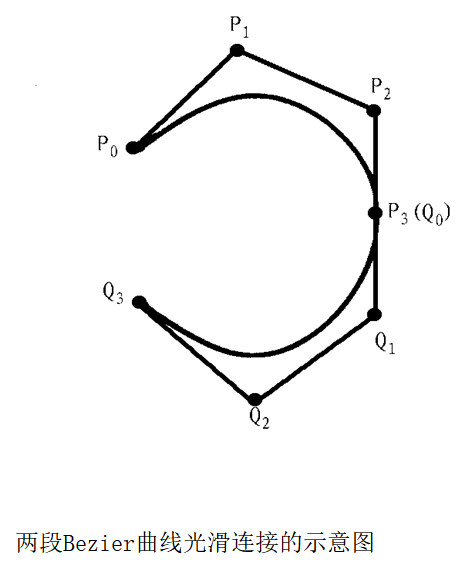
一阶导数连续

第一段曲线终点处的导数为：P’(1)﹦3(P3﹣P2)
第二段曲线起点处的导数为：Q’(0)﹦3(Q1﹣Q0)
所以，若要满足一阶导数连续，需要：P3﹣P2﹦Q1﹣Q0（当前点-前一点=后一点-当前点）

二阶导数连续

第一段曲线终点处的二阶导数为：P”(1)﹦6(P3-2P2+P1)
第二段曲线起点处的二阶导数为：Q”(0)﹦6(Q2-2Q1+Q0)
要达到二阶导数连续：P3-2P2+P1=Q2-2Q1+Q0
整理后可得：Q2-P1=2(Q1-P2)（后两点-前两点=2(后一点-前一点)）

三次Bezier曲线例子

设在平面上给定的7个控制点坐标分别为:A（100,300）,B（120,200）, C（220,200）,D（270,100）,E（370,100）,F（420,200）,G（420,300）。画出其曲线。若想在D点达到C1连续，请问E点的坐标应该移动到哪里？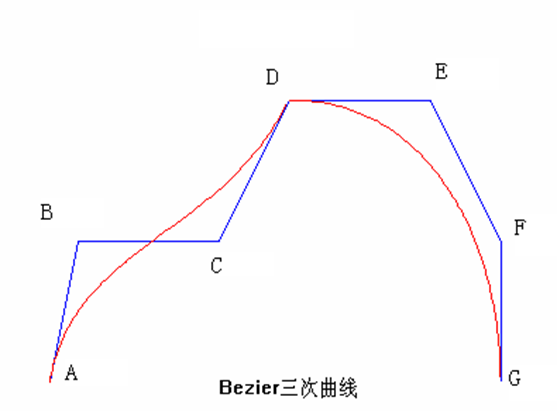

解：满足C1连续，需要PD-PC=QE-QD，所以(270,100)-(220,200)=(x,y)-(270,100)，解得(x,y)=(320,0)

设在平面上给定的7个控制点坐标分别为:A（100,300）,B（120,200）, C（220,200）,D（270,100）,E（320,0）,F（420,200）,G（420,300）。若想在D点达到C2连续，请问F点的坐标应该移动到哪里？F点的x值为（ ）， y值为（ ）。
解：满足C2连续，需要QF-PB=2(QE-PC)，所以(x,y)-(120,200)=2((320,0)-(220,200))，解得(x,y)=(320,-200)