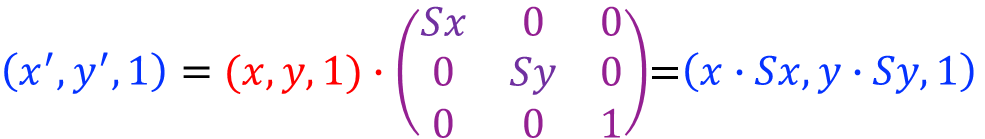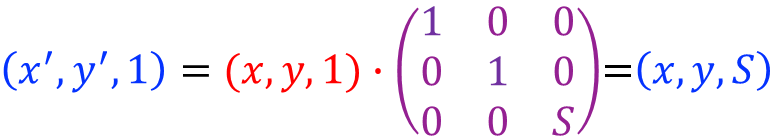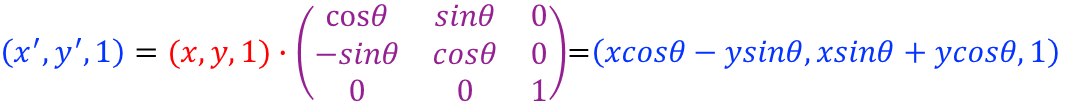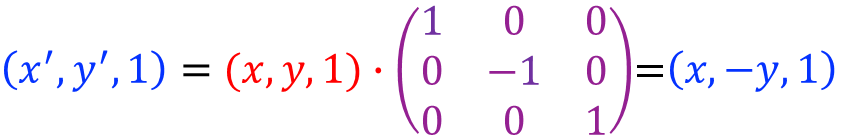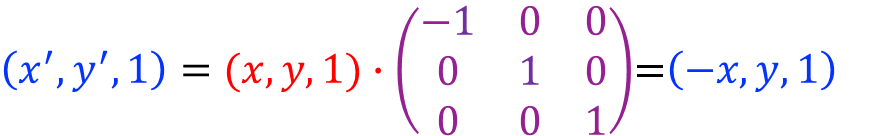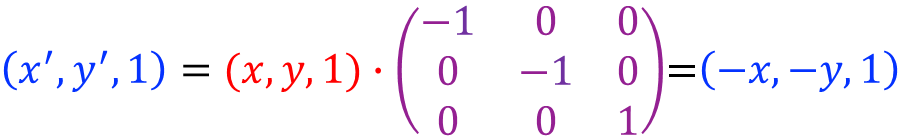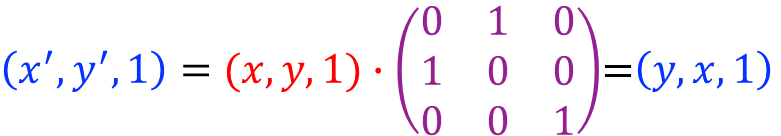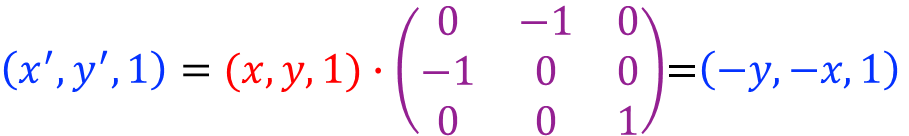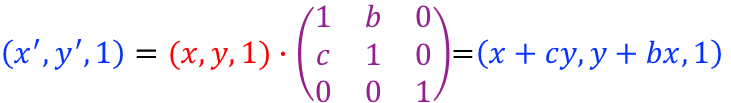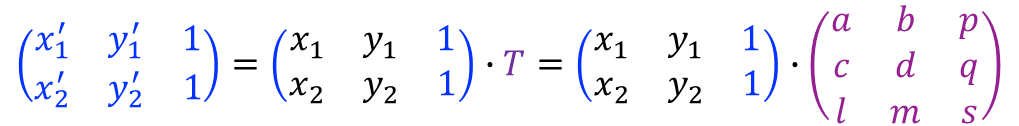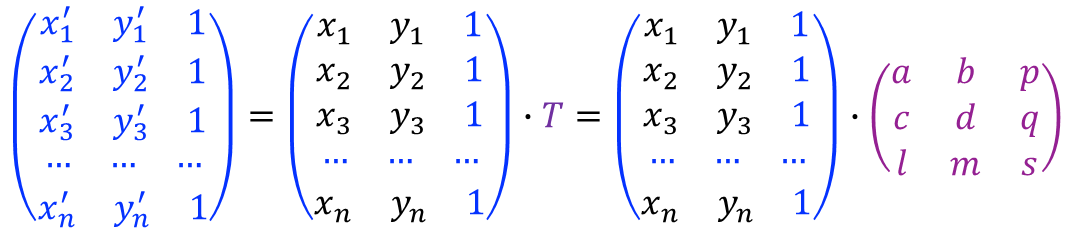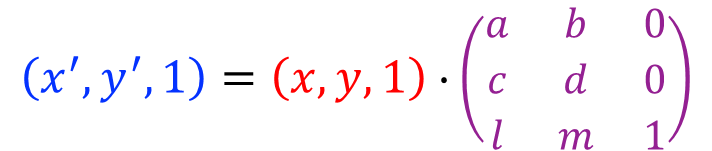基本概念

在定义了规范化齐次坐标后，图形变换可以表示为图形点集的规范化齐次坐标矩阵与某一变换矩阵进行矩阵相乘的形式。

基本几何变换

平移

比例

整体比例

旋转

• 旋转：是指将P绕坐标原点逆时针转动θ角度得到新的点P’ 的重定位过程。
• 规定：逆时针转动的角度为正，顺时针转动的角度为负。
• 顺时针旋转θ角度 ó 逆时针旋转-θ(或2π-θ)角度

对称

关于x轴对称

关于y轴对称

关于原点对称

关于y=x对称

关于y=-x对称

错切

b、c正负分别代表沿着y、x轴正负方向错切。

泛化

二维图形的几何变换均可表示成图形中点集的齐次坐标与3阶的二维变换矩阵T的乘法形式。

直线的变换

多边形的变换

其他

其他曲线、多边形的变换也同样将点阵构成的矩阵与几何变换矩阵进行左乘。

复合变换

复合变换：图形作一次以上的几何变换，变换结果是每次的变换矩阵相乘。任何一个复杂的几何变换都可以看作基本几何变换的组合形式。

各类复合变换

• 平移：相加
• 比例：相乘
• 旋转：角度相加，错切和整体比例变换的复合。

  相对任一参考点的二维几何变换

1. 对坐标系进行平移，使得原坐标系下的参考点(x_F,y_F )为新坐标系的坐标原点；
2. 针对原点进行二维几何变换；
3. 将坐标系反平移回原始坐标系。

相对任意方向的二维几何变换

1. 对坐标系进行旋转，使得(0,0)→(1,1)在新坐标系下与x轴重合；
2. 针对x轴进行比例变换；

将坐标系反向旋转回原始坐标系。

若给出的任意方向不经过坐标原点应该怎么办？

1. 将A点平移至坐标原点，得到A’B’；
2. 对坐标系进行旋转，使得A’B’在新坐标系下与坐标轴重合；
3. 针对坐标轴进行二维几何变换；
4. 将坐标系反向旋转回原始坐标系；

5. 将坐标原点反平移至A点。

   变换的性质

   仿射变换具有平行线不变性和有限点数目的不变性。
   二维仿射变换是具有如下形式的二维坐标变换：
   

   性质

6. 直线的中点不变性；

7. 平行直线不变性；
8. 相交不变性；
9. 仅包含旋转、平移和反射的仿射变换维持角度和长度的不变性；
10. 比例变换可改变图形的大小和形状；
11. 错切变换引起图形角度关系的改变，甚至导致图形发生畸变。