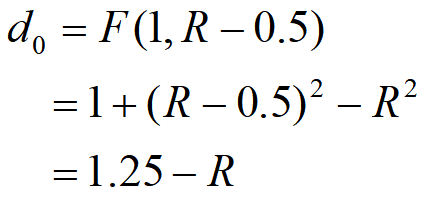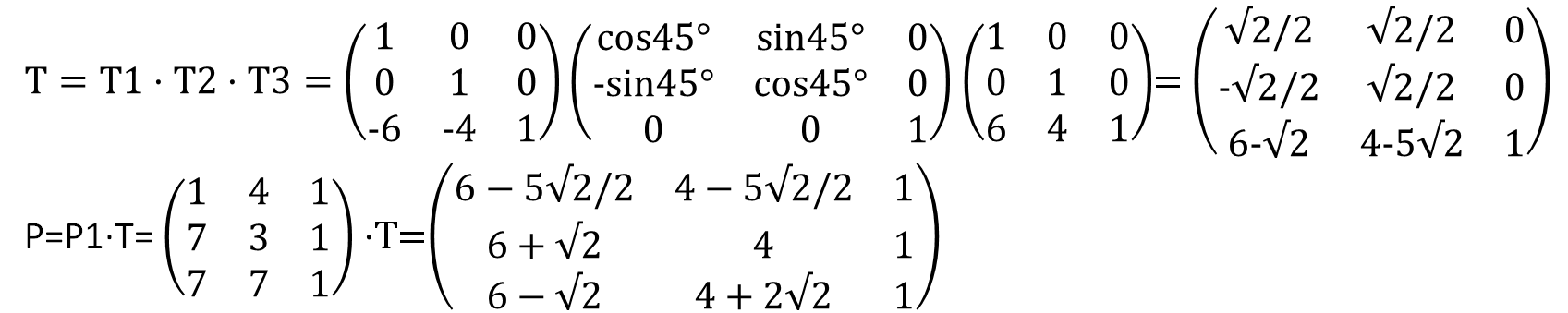填空题

  1. 一个交互式计算机图形系统的功能应包括：交互、计算、存储、输入和输出。
  2. 区域可以由内部点或边界来定义，在泛填充算法中假设区域采用内部点定义。
  3. 在裁剪算法中主要解决两个问题：第一是判断计算图形在区域内部或外部，第二是计算图形与裁剪区域边界的交点。
  4. Bezier曲线P(t)，对于任意给定的t，P(t)是特征多边形各顶点的加权平均。
  5. 椭圆的Bresenham生成算法，通常把椭圆分成4个部分。
  6. 偏转系统的主要功能是。
  7. 基本几何变换是相对于坐标原点和坐标轴进行的几何变换，有平移、比例、旋转和错切等。
  8. 一个交互式计算机图形处理系统由图形软件和图形设备两部分组成。
  9. 区域是指已经表示成点阵形式的填充图形，它是像素集合。通常有内点表示和边界表示两种形式。
  10. 写出3个计算机图形学的应用领域：科学计算可视化、地理信息系统、虚拟现实。

  11. 电子枪的主要功能是产生一个沿管轴方向(Z轴)前进的细电子束轰击荧光屏。

    名词解释

    图形

    以矢量图形式呈现，计算机中由景物的几何模型与物理属性表示的图形。能体现几何个体，记录体元的形状参数与属性参数。如图纸。

    图像

    以点阵图形式呈现，它更强调整体形式，记录点及它的灰度或色彩。例如照片、扫描图片和由计算机产生的真实感和非真实感图形等。

    齐次坐标系

    齐次坐标表示就是用n+1维向量表示一个n维向量。

    参数连续性

    如果它在t_i处n阶左右导数存在，称曲线P = P(t)在t=t_i处n阶参数连续，并且满足：
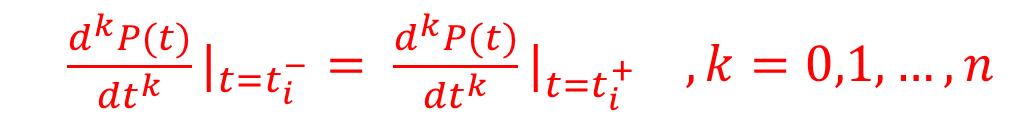
    image.png

    • 记号期末考试复习题 - 图2
    • 若曲线在区间[0,1]内处处是期末考试复习题 - 图3连续的，则曾该曲线是期末考试复习题 - 图4连续的。
    • 期末考试复习题 - 图5连续传统的、严格的连续性。

      几何连续性

  • 只需限定两个曲线段在交点处的参数导数成比例，而不必完全相等。
  • 记号期末考试复习题 - 图6
  • 直观的、易于交互控制的连续性

注意：如果一阶导比例是a，而二阶导比例是b，a和b之间毫无关系。

平面几何投影

主要指平行投影、透视投影以及通过这些投影变换而得到的三维立体的常用平面图形：三视图、轴测图、透视图等。

灭点

灭点可以看作是无限远处的一点在投影面上的投影。
不平行于投影面的平行线的投影会汇聚到一个点，这个点称为灭点(Vanishing Point)。

图形几何变换

图形的几何变换是指对图形的几何信息经过平移、比例、旋转等变换后产生新的图形，是图形在方向、尺寸和形状方面的变换。

图形的扫描转换

在光栅显示器等数字设备上确定一个最佳逼近于图形的像素集的过程。逼近过程就是连续量向离散量转换的过程。

Bezier曲线的定义式

image.png

简答题

Cohen-Sutherland算法

写出Cohen-Sutherland算法中直线端点的编码规则，并画图写出相应的9个区域的编码。

DDA算法

写出用直线的DDA算法扫描直线段P0(0,0)—P1(5,2)时，所经过的点。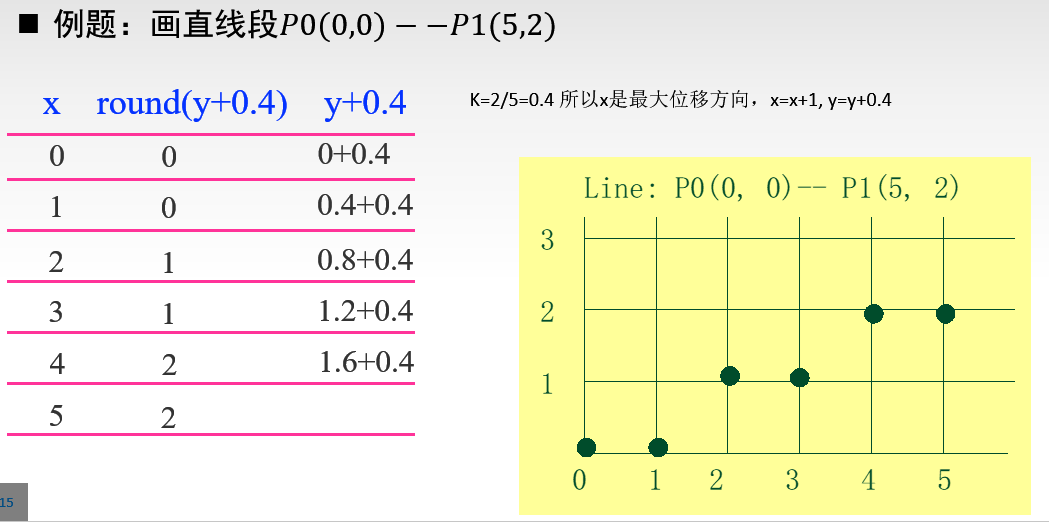
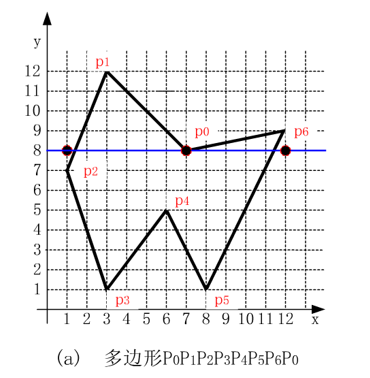
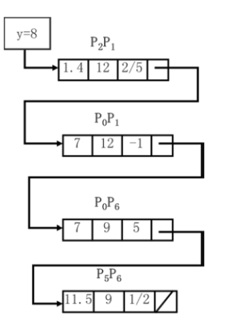
image.png

有效边表算法

写出途中扫描线8处的有效边表。
image.pngimage.png

Weiler-Atherton算法

写出Weiler-Atherton多边形裁剪的思想及算法步骤。
思想：假设多边形按顶点的顺时针方向进行表示，那么，沿多边形的边进行裁剪时，由不可见侧进入可见侧时，输出可见线段的两个端点（比如对于AB，输出P、B）；由可见侧进入不可见侧时，输出交点，并从当前交点沿窗口边界的顺时针方向找最近的交点，并输出。（比如：对于BC，输出Q，并沿窗口顺时针找到最近交点P,输出P)
算法步骤：假定按顺时针方向处理顶点，将用户多边形定义为Ps，窗口矩形为Pw。算法首先计算出Ps与Pw的所有交点。然后，从Ps的任一点出发，跟踪检测Ps的每一条边，当Ps与Pw相交时（实交点），按如下规则处理：

  1. 若是由不可见侧进入可见侧，则输出可见直线段，转(3)；
  2. 若是由可见侧进入不可见侧，则从当前交点开始，沿窗口边界顺时针检测Pw的边，即用窗口的有效边界去裁剪Ps的边，找到Ps与Pw最靠近当前交点的另一交点，输出可见直线段和由当前交点到另一交点之间窗口边界上的线段，然后返回处理的当前交点；

  3. 沿着Ps处理各条边，直到处理完Ps的每一条边，回到起点为止。

    Bresenham算法

    写出用直线的中点Bresenham算法扫描直线段P0(0,0)—P1(5,2)时，所经过的点。
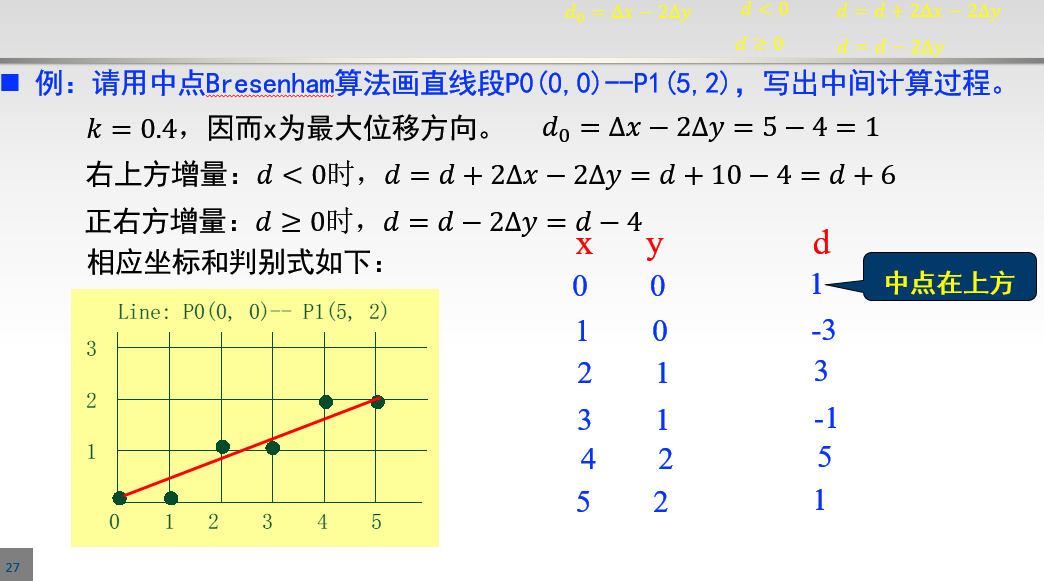
    image.png

    二维变换

    写出二维齐次坐标变换矩阵并说明各子矩阵的功能。
    image.png

    计算题

    二维变换

  4. 已知三角形ABC各顶点的坐标A(1,2)、B(7,2)、C(4,5)，相对直线Y=6做对称变换后到达A’、B’、C’。试计算A’、B’、C’的坐标值。（要求用齐次坐标进行变换，写出变换矩阵）

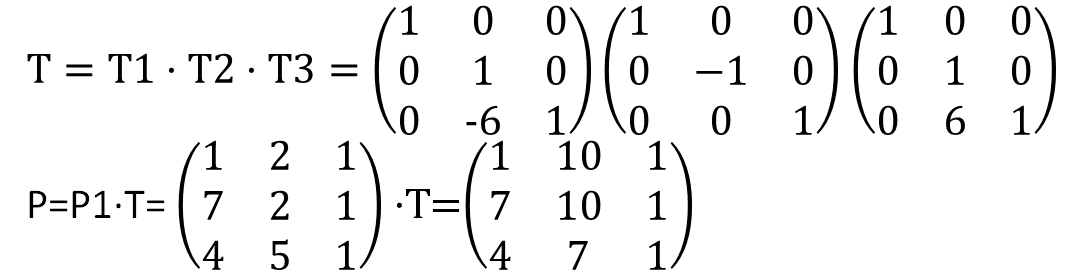
image.png

  1. 已知三角形ABC各顶点的坐标A(1,4)、B(7,3)、C(7,7)，相对P(6,4)点旋转45°的变换矩阵，并求出各端点的坐标，画出变换后的图形。（要求用齐次坐标进行变换，写出变换矩阵）

image.png

中点Bresenham算法

  1. 试用中点Bresenham算法原理推导椭圆的扫描转换算法。（要求写清原理、误差函数和递推公式）

原理：

  1. 从(0,b)到(a,0)顺时针地确定最佳逼近于第一象限椭圆弧的像素序列。
  2. 在上半部分， -1 ≤ k ≤0 , 最大位移方向为x;
  3. 在下半部分， k ≤-1 , 最大位移方向为y;
  4. 分别对上半部分和下半部分依次判断中点与椭圆边的关系，即：判别式的符号。

误差函数：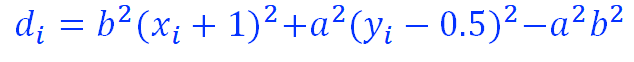
image.png

  • 若di≤0，取P_u (x_i+1,y_i )
  • 若di>0，取P_d (x_i+1,y_i-1)

递推公式：
image.pngimage.png

  1. 试用中点Bresenham算法原理推导圆的扫描转换算法。（要求写清原理、误差函数和递推公式）

原理：
构造函数期末考试复习题 - 图18

  • 对于圆上的点，有𝐹(𝑥,𝑦)=0；
  • 对于圆外的点，𝐹(𝑥,𝑦)>0；

  • 而对于圆内的点，𝐹(𝑥,𝑦)<0。

  • 当𝐹(𝑥𝑀,𝑦𝑀)<0时，取𝑃𝑢 (𝑥𝑖+1,𝑦𝑖 )

  • 当𝐹(𝑥𝑀,𝑦𝑀 )>0时，取𝑃𝑑 (𝑥𝑖+1,𝑦𝑖−1)
  • 当𝐹(𝑥𝑀,𝑦_𝑀 )=0时，约定取𝑃𝑢

中点M的坐标为：M(x_i+1,y_i-0.5)，
误差函数：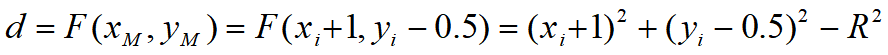
image.png
•当d_i≤0时，下一点取P_u (x_i+1,y_i );
•当d_i>0时，下一点取P_d (x_i+1,y_i-1)
递推公式：
image.pngimage.png
初始值：
image.png