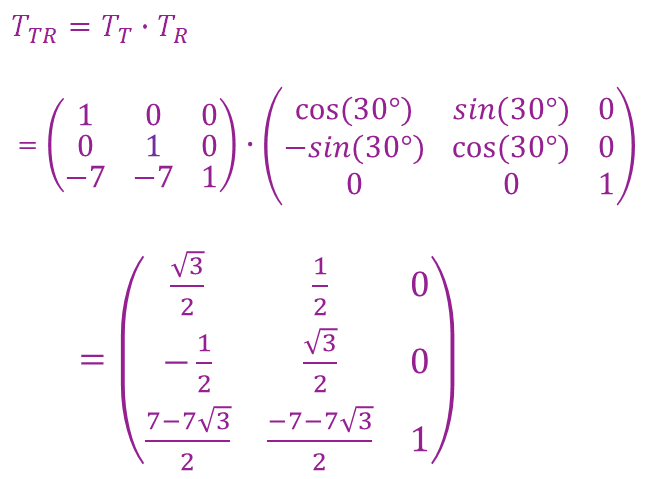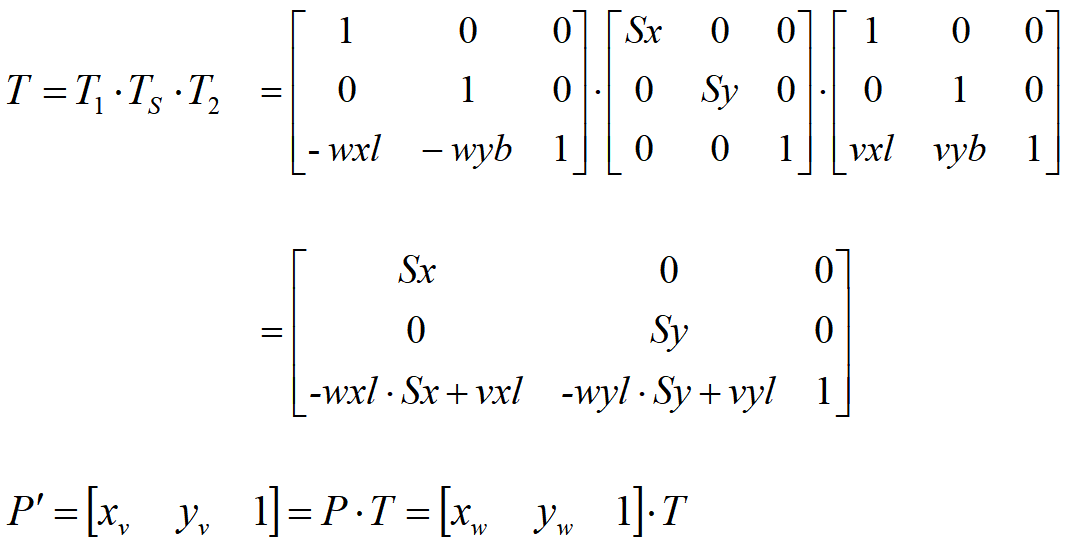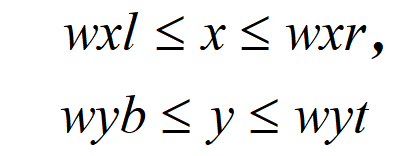二维观察

基本概念

坐标系z

• 用户坐标系：纸上的图形采用的坐标是实数域中的直角坐标系或是极坐标系，统称为用户坐标系。

• 设备坐标系：屏幕上采用的坐标系是整数域中直角坐标系，这类坐标系统称为设备坐标系。

  窗口和视区

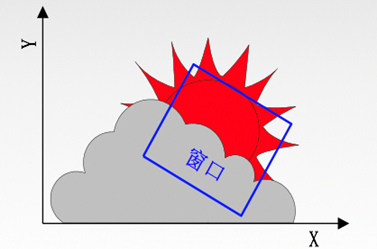
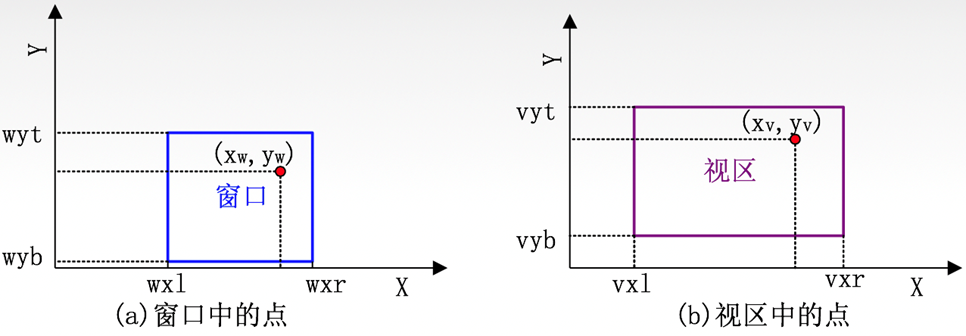
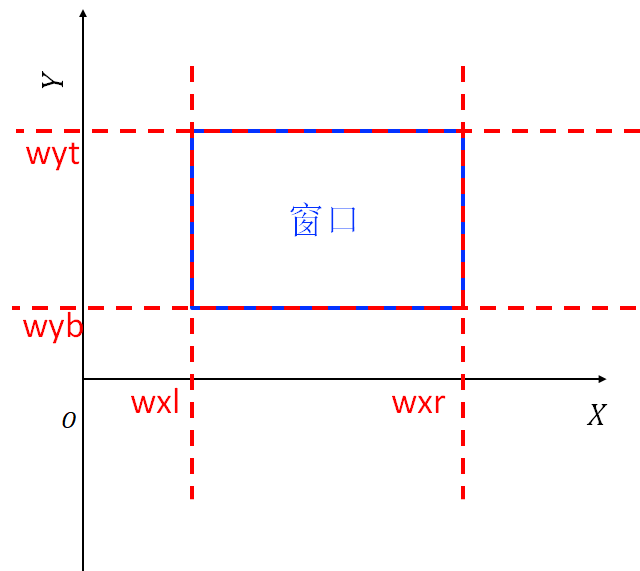
• 窗口：在计算机图形学中，将在用户坐标系中需要进行观察和处理的一个坐标区域称为窗口（Window）。

• 视区（也叫视口）：为了在屏幕上指定显示图形的位置，在屏幕上定义一个矩形，该矩形称为视区，窗口内的图形就显示在屏幕上的视区中。即：将窗口映射到显示设备上的坐标区域称为视区（Viewport）。

  用户坐标系向设备坐标系（即：屏幕坐标系）的变换

1. 将用户坐标系中任意范围区域转换到屏幕某个范围区域，从而用户坐标系此范围区域内的图形也转换到屏幕上该范围区域内。（即：窗口到视区的变换）

2. 用户坐标系此区域内图形上的坐标值转换到屏幕上该范围区域内后不一定是整数，取整后才成为该范围区域内的屏幕坐标值。（即：用户坐标系下窗口的坐标变换后不一定是整数，因而涉及到四舍五入）

3. 用户坐标右手系到屏幕坐标左手系的坐标轴方向变换；
4. 当屏幕坐标系水平方向与垂直方向刻度不等时，为保持图形不走样，还要进行比例变换。

   观察变换

   要将窗口内的图形在视区中显示出来，必须经过将窗口到视区的变换（Window-Viewport Transformation）处理，这种变换就是观察变换（Viewing Transformation）。变换时为了方便计算，通常，引入观察坐标系(View Coordinates)和规格化设备坐标系(Normalized Device Coordinates) 。

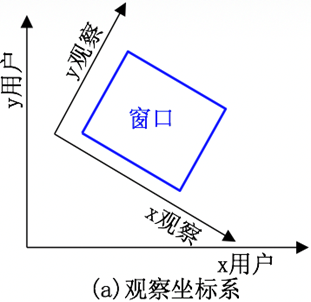
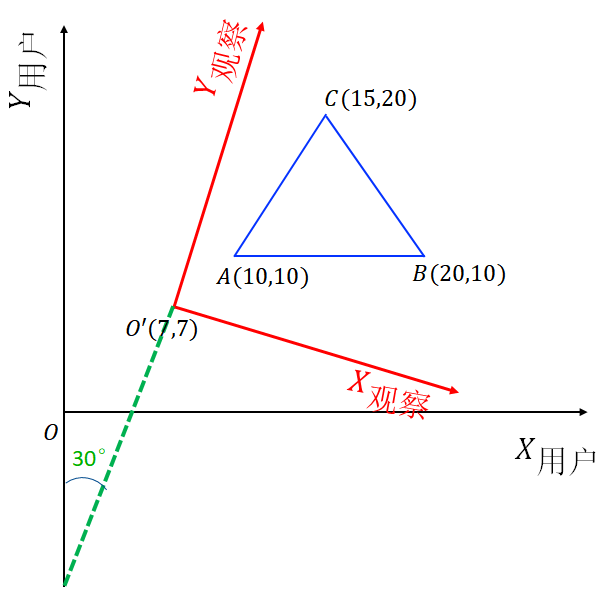
• 观察坐标系**：**依据窗口的方向和形状在用户坐标平面中定义的直角坐标系。
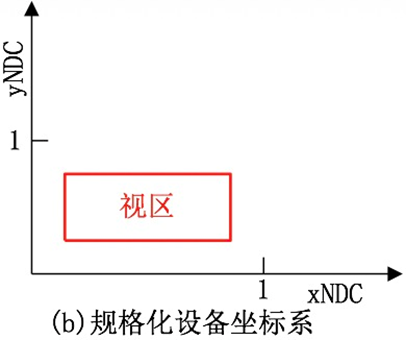
• 规格化设备坐标系：将二维的设备坐标系规格化到（0.0，0.0）到（1.0，1.0）的坐标范围内形成的。

二维观察流程

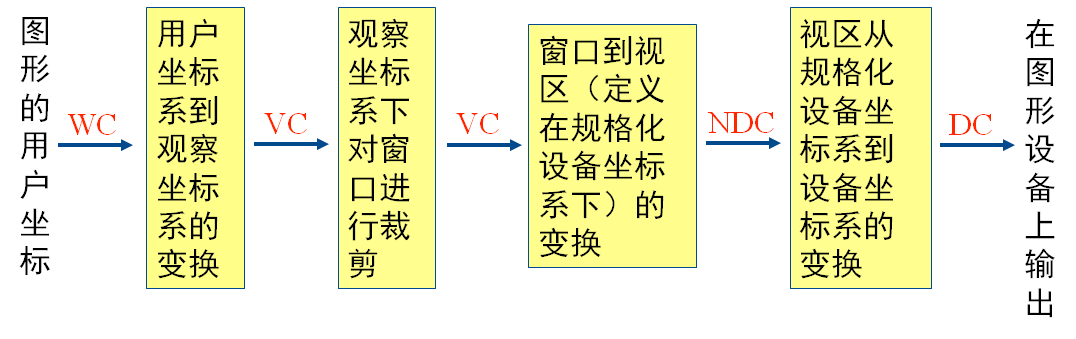
• 变焦距效果：窗口变，视区不变

• 整体缩放效果：窗口不变，视区变

  用户坐标系到观察坐标系的变换

  
  

  窗口到视区的变换

  平移->比例变换->反平移
  
  

  裁剪

  

  点的裁剪

  

  直线段的裁剪

  Cohen-Sutherland算法

  区域编码

  

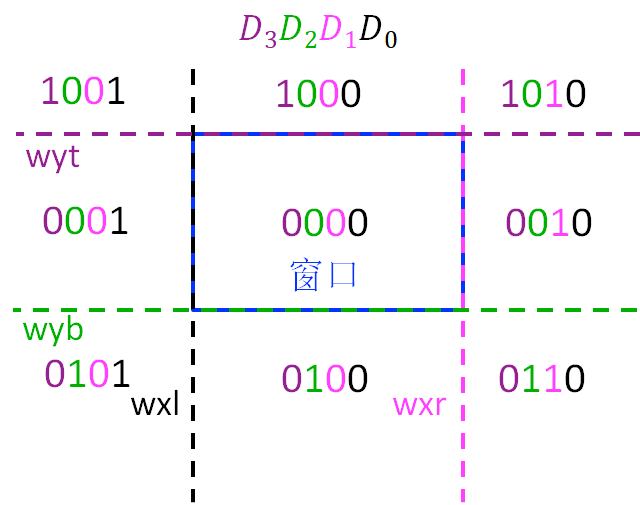
• 若x<wxl，则D0=1，否则D0=0；

• 若x>wxr，则D1=1，否则D1=0；
• 若y<wyb，则D2=1，否则D2=0；
• 若y>wyt， 则D3=1，否则D3=0。

  算法原理

  编码=0简取，编码!=0简弃，否则求交。

  算法步骤

1. 输入直线段的两端点坐标：P1(x1,y1)、P2(x2,y2)，以及窗口的四条边界坐标：wyt、wyb、wxl和wxr；
2. 对P1、P2进行编码：点P1的编码为code1，点P2的编码为code2；
3. 若code1|code2=0，对直线段应简取之，转(6)；否则，若code1&code2≠0，对直线段可简弃之，转(7)；当上述两条均不满足时，进行步骤(4)；
4. 确保P1在窗口外部：若P1在窗口内，则交换P1和P2的坐标值和编码；
5. 计算直线段与code1中编码等于1对应窗口边界的交点，并用该交点的坐标值替换P1的坐标值。也即在交点S处把线段一分为二，并去掉P1S这一段。考虑到P1是窗口外的一点，因此可以去掉P1S。转(2);
6. 用直线扫描转换算法画出当前的直线段P1P2;
7. 算法结束。

   算法特点
   

   本算法用编码的方法实现了对完全可见和完全不可见直线段的快速接受和拒绝，在两种裁剪场合非常高效：

• 窗口特别大的场合
• 窗口特别小的场合

  中点分割算法

  基本思想

  当对直线段不能简取也不能简弃时，简单地把线段等分为二段，对两段重复上述测试处理，直至每条线段完全在窗口内或完全在窗口外。

  算法步骤

1. 输入直线段的两端点坐标：P1(x1,y1)、P2(x2,y2)，以及窗口的四条边界坐标：wyt、wyb、wxl和wxr；
2. 对P1、P2进行编码：点P1的编码为code1，点P2的编码为code2；
3. 若code1|code2=0，对直线段应简取之，保留当前直线段的端点坐标，转(5)；否则，若code1&code2≠0，对直线段可简弃之，转(5)；当上述两条均不满足时，进行步骤(4)；
4. 求出直线段的中点M，将P1M、P2M入栈；
5. 当栈不空时，从栈中弹出一条直线段，记为P1P2，转(2)进行处理。否则，继续(6)；
6. 当栈为空时，合并保留的直线段端点，得到窗口内的直线段P1P2。用直线扫描转换算法画出当前的直线段P1P2，算法结束。

存在一个问题：当一个点在窗口边缘，另一个点在窗口外时，不能简弃也不能简取。

改进的算法步骤（By牛冬梅）

1. 输入直线段的两端点坐标：P1(x1,y1)、P2(x2,y2)，以及窗口的四条边界坐标：wyt、wyb、wxl和wxr；
2. 对P1、P2进行编码：点P1的编码为code1，点P2的编码为code2；
3. 若code1|code2=0，对直线段应简取之，保留当前直线段的端点坐标，转(5)；否则，若code1&code2≠0，对直线段可简弃之，转(7)；当上述两条均不满足时，进行步骤(4)；
4. 若code1=0且P1为窗口边界上的点，判断P1和P2是否在窗口边界的同一侧，若在同一侧，则简弃之，转(7)，否则转(6); 否则转(5);
5. 若code2=0且P2为窗口边界上的点，判断P1和P2是否在窗口边界的同一侧，若在同一侧，则简弃之，转(7)，否则转(6); 否则转(6):
6. 求出直线段的中点M，将P1M、P2M入栈；
7. 当栈不空时，从栈中弹出一条直线段，记为P1P2，转(2)进行处理。否则，继续(6)；
8. 当栈为空时，合并保留的直线段端点，得到窗口内的直线段P1P2。用直线扫描转换算法画出当前的直线段P1P2，算法结束。

中点分割算法的核心思想是通过二分逼近来确定直线段与窗口的交点。
对于上述两种算法，均需要计算中点分割后的两段，可以再次改进以减少其计算次数：

改进的中点分割算法步骤

1. 若code1|code2=0，对直线段应简取之，结束；否则，若code1&code2≠0，对直线段可简弃之，结束；当这两条均不满足时，进行步骤(2)；
2. 找出该直线段离窗口边界最远的点和该直线段的中点。判中点是否在窗口内：若中点不在窗口内，则把中点和离窗口边界最远点构成的线段丢掉，以线段上的另一点和该中点再构成线段求其中点；若中点在窗口内，则又以中点和最远点构成线段，并求其中点，直到中点与窗口边界的坐标值在规定的误差范围内相等，则该中点就是该线段落在窗口内的一个端点坐标；
3. 如另一点在窗口内，则经(2)即确定了该线段在窗口内的部分。如另一点不在窗口内，则该点和所求出的在窗口上的那一点构成一条线段，重复步骤(2)，即可求出落在窗口内的另一点。

   参数化线段裁剪算法

   (梁友栋-Barsky线段裁剪算法) 算法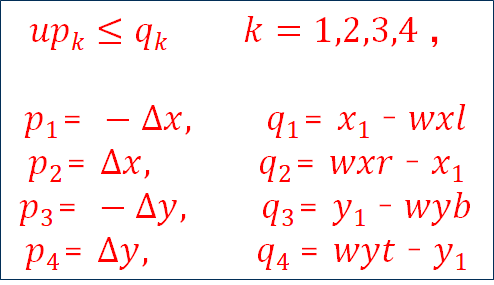
   
   如果u1＞u2，则线段完全落在裁剪窗口之外，应被舍弃。否则被裁剪线段可见部分的端点由参数u1和u2计算出来。

   例题

   
   

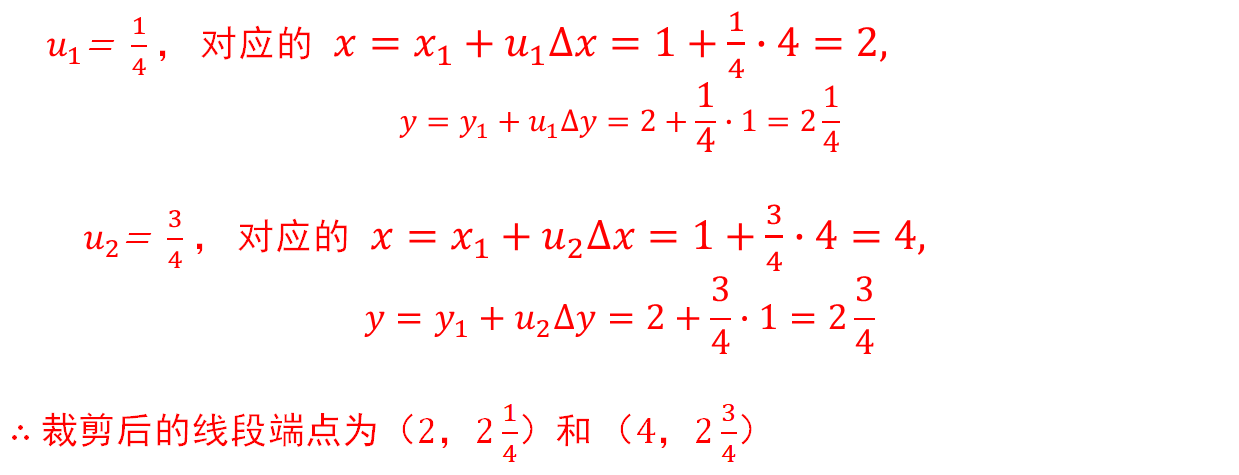
   特点

   梁友栋-Barsky线段裁剪算法通常比Cohen－Sutherland算法效率更高，因为计算参数u1和u2仅仅需要除法，而Cohen－Sutherland算法每次求交都要计算乘除法。

   多边形的裁剪

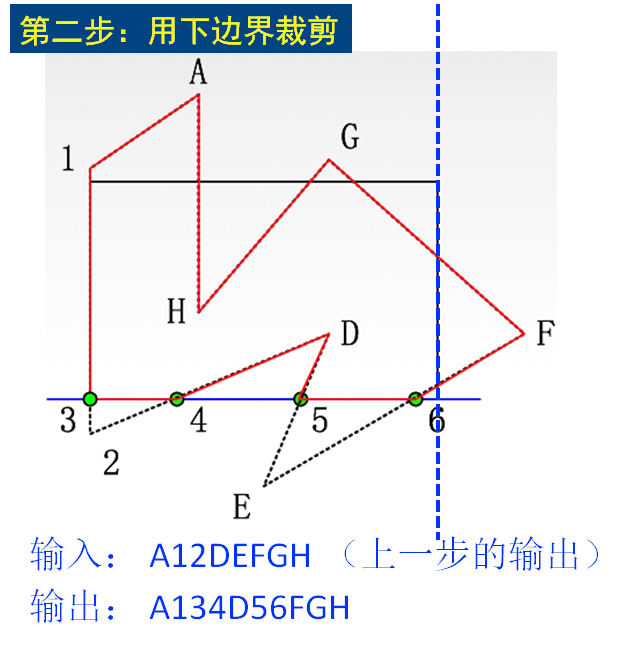
   Sutherland-Hodgeman多边形裁剪算法（S-H多边形裁剪算法）

   逆时针绕一圈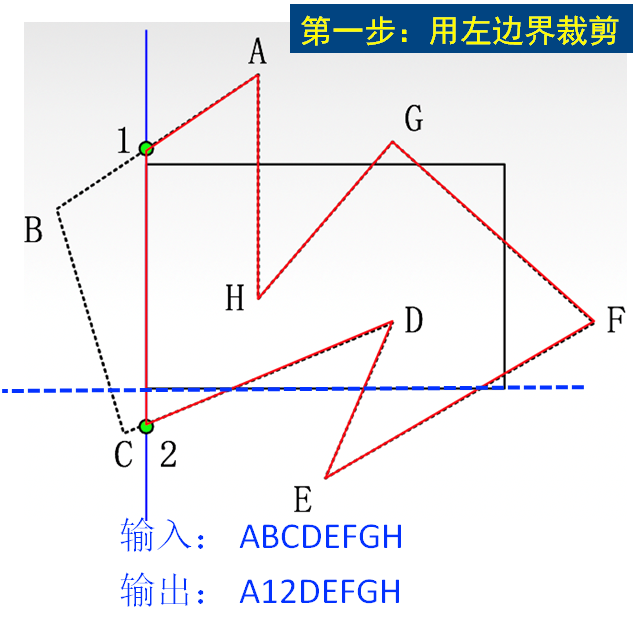
   
   

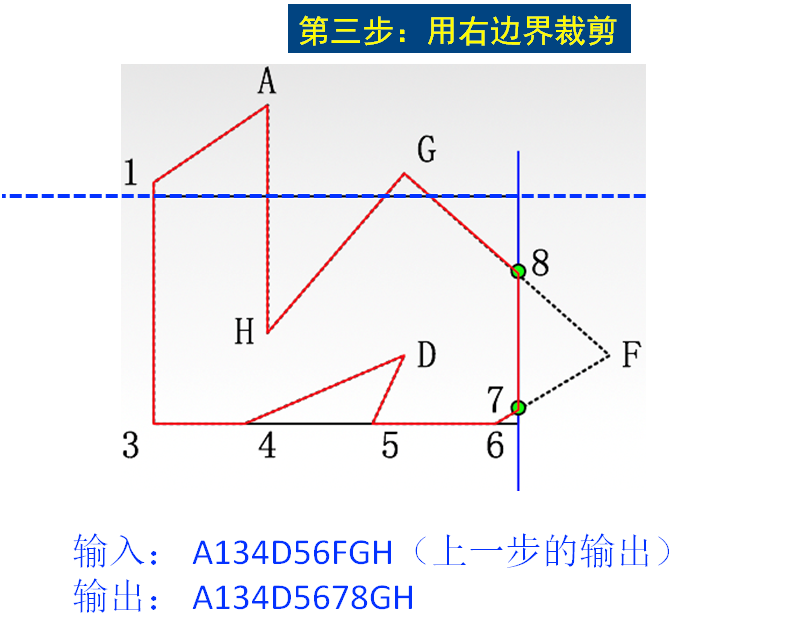
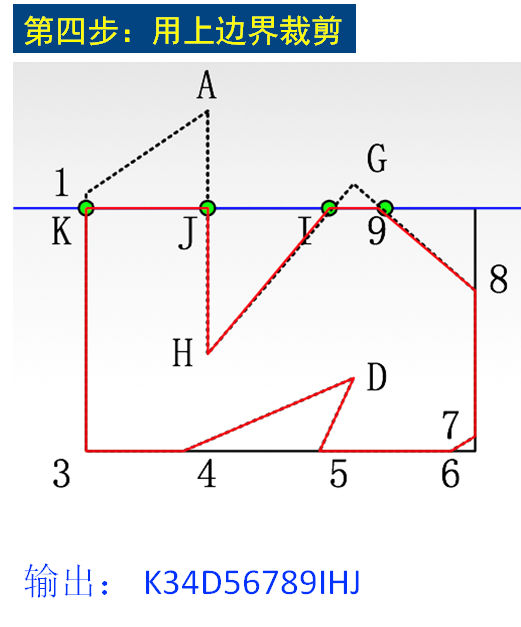
   Weiler-Atherton 多边形裁剪算法（W-A多边形裁剪算法）

   
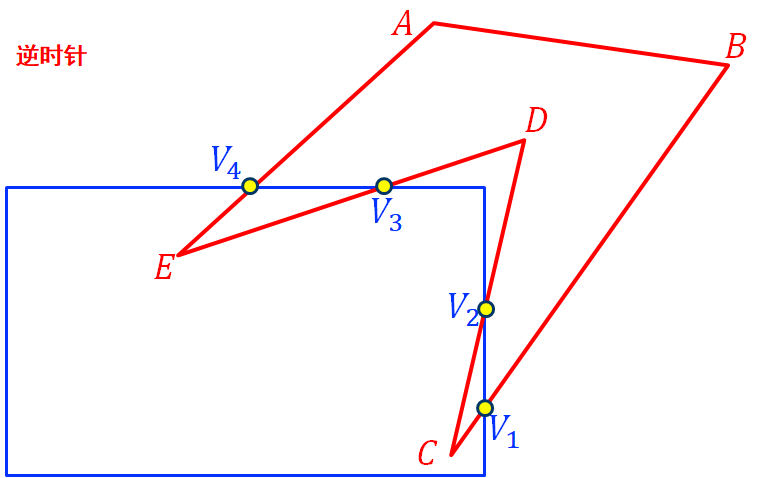
   ∵CB由可见侧进入不可见侧；∴保留V_1，并从V_1 出发，沿窗口边界逆时针找最近交点，最近交点为V_2 ， ∴保留V_2 并回到V_1；继续处理BA, ∵BA位于窗口之外，∴简弃之；至此，所有的边均处理完毕。保留的顶点序列为：V_4 、E、V_3 、V_4 、V_2 、C、V_1 、V_2；其中，V_4 、E、V_3 、V_4 构成一个封闭的多边形，V_2 、C、V_1 、V_2构成一个封闭的多边形。
   注意：多边形的外边界如果用顺时针，那么内边界就用逆时针。