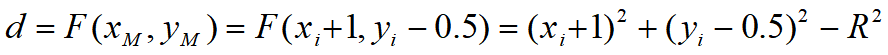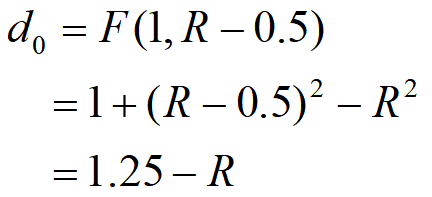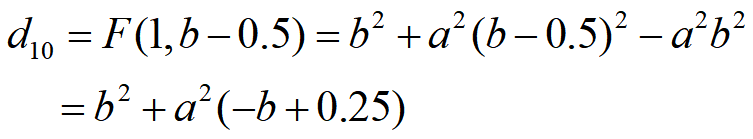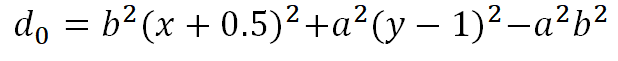定义
图形的扫描转换
- 图形的扫描转换:在光栅显示器等数字设备上确定一个最佳逼近于图形的像素集的过程。
- 逼近的过程就是连续量向离散量转换的过程。
基本图形生成算法
直线的扫描转换
数值微分法(DDA:
Digital Differential Analyzer)
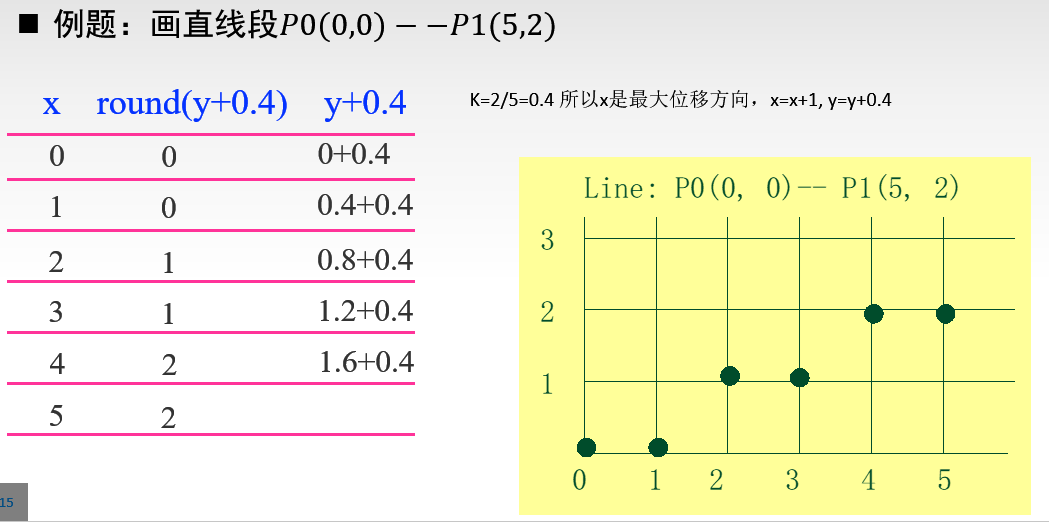
特点:
- 增量算法(最大位移方向+1或-1)
- 直观、易实现
- 在此算法中,x、y、k必须是float,且每一步都必须对x、y进行舍入取整,不利于硬件实现。
中点Bresenham算法
(x为最大位移方向,
时y为最大位移方向)时Bresenham算法的算法步骤为:
- 输入直线的两端点P0(x0,y0)和Pn(xn,yn);
- 计算初始值
- 0<=|k|<=1:
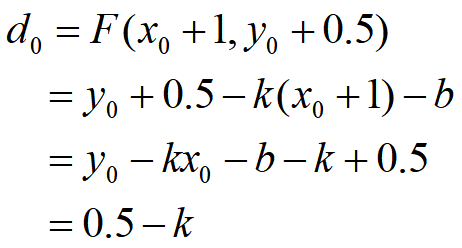
- |k|>1:
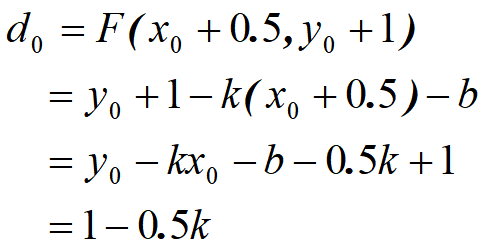
- 0<=|k|<=1:
- 绘制点(x,y)。判断d的符号;
- 若d<0,则(x,y)更新为(x+1,y+1),d更新为 d+1-k;
- 否则(x,y)更新为(x+1,y),d更新为 d-k。
-
用2d∆x代替d
输入直线的两端点P0(x0,y0)和Pn(xn,y_n);
- 计算初始值
- 绘制点(x,y)。判断d的符号;
- 若d<0,则(x,y)更新为(x+1,y+1),d更新为 d+2∆x-2∆y;
- 否则(x,y)更新为(x+1,y),d更新为 d-2∆y。
-
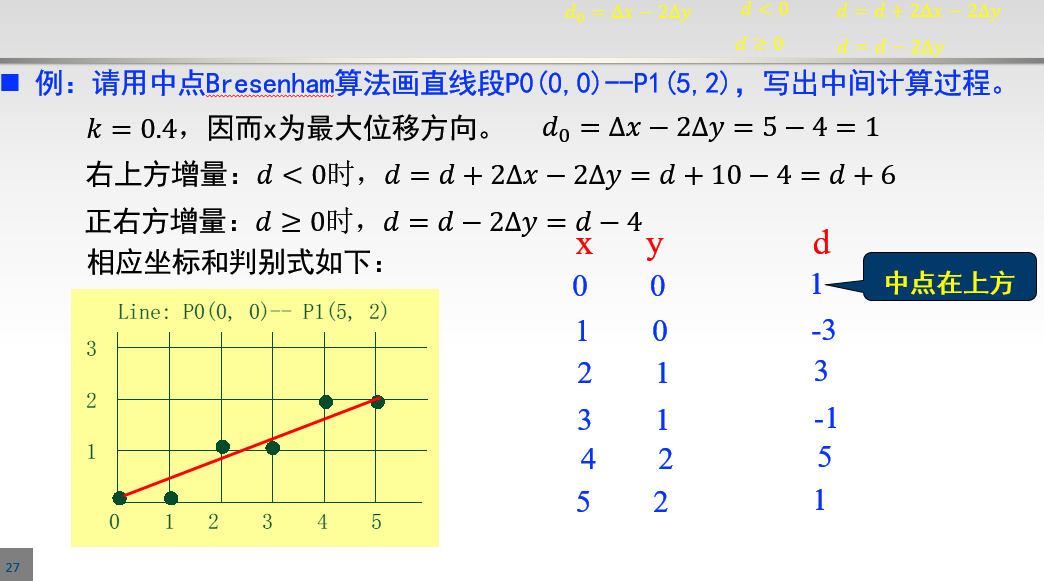
例题
改进的Bresenham算法
算法步骤
输入直线的两端点P0(x0,y0)和Pn(xn,y_n);
- 计算初始值△x、△y、d=0、x=x0、y=y0;
- 绘制点(x,y);
- d更新为d+k,判断d的符号。若d>0.5,则(x,y)更新为(x+1,y+1),同时将d更新为d-1;否则(x,y)更新为(x+1,y);
-
改进1:为计算方便,令e=d-0.5

输入直线的两端点P0(x0,y0)和Pn(xn,y_n);
- 计算初始值△x、△y、e=-0.5、x=x0、y=y0;
- 绘制点(x,y);
- e更新为e+k,判断e的符号。若e>0,则(x,y)更新为(x+1,y+1),同时将e更新为e-1;否则(x,y)更新为(x+1,y)。
- 当直线没有画完时,重复步骤3和4。否则结束。
改进2:为方便硬件实现,做以下改进摆脱小数、除法运算:用2e∆x来替换e

- 输入直线的两端点P0(x0,y0)和Pn(xn,y_n);
- 计算初始值△x、△y、e=-∆x、x=x0、y=y0;
- 绘制点(x,y);
- e更新为e+2∆y,判断e的符号。若e>0,则(x,y)更新为(x+1,y+1),同时将e更新为e-2∆x;否则(x,y)更新为(x+1,y)。
- 当直线没有画完时,重复步骤3和4。否则结束。
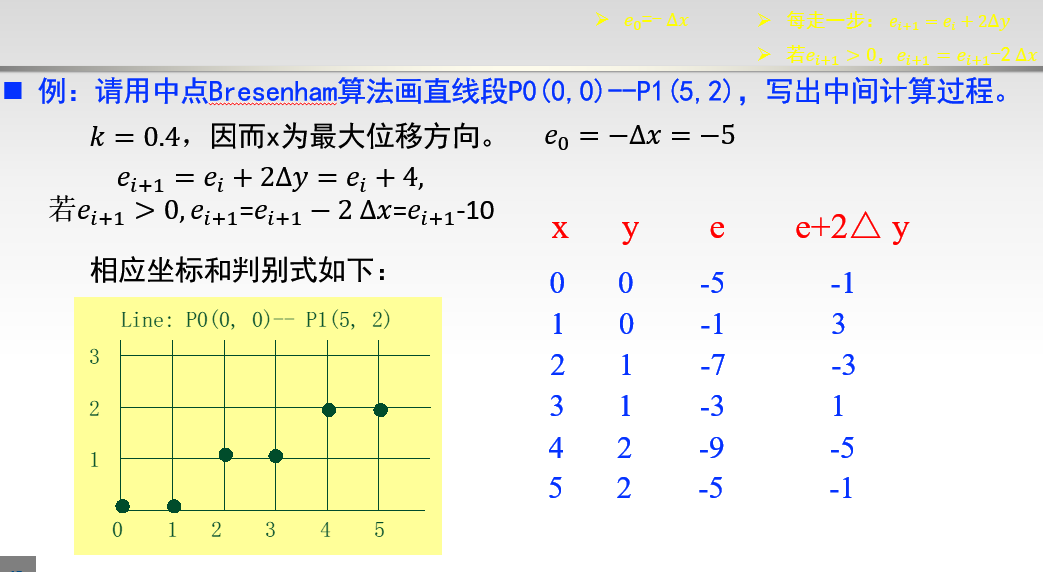
例题
圆的扫描转换
简单方程生成圆弧
极坐标下的参数离散化: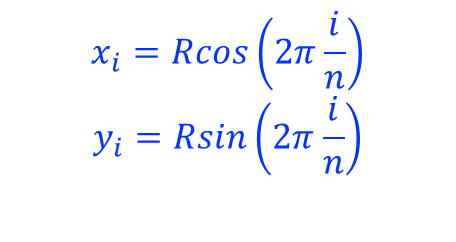
数值微分算法(DDA)画圆
基本原理
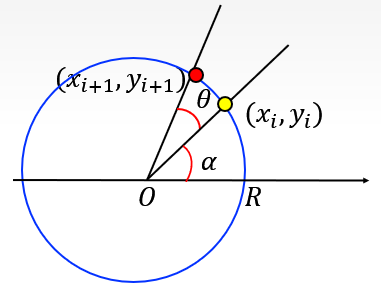
通过极限思想,逐渐将变化度转化为一个极小量:
当q
足够小时有:
方程
可以改写为:
习惯上用e
表示一个较小的量,用它替代q,式子改写为:
特点
- 简单、直观
- 计算量大
-
中点Bresenham算法画圆
原理
只对(2/Π,4/Π)的八分之一圆进行绘制,其他部分通过对称得到。
构造函数 对于圆上的点,有𝐹(𝑥,𝑦)=0;
- 对于圆外的点,𝐹(𝑥,𝑦)>0;
而对于圆内的点,𝐹(𝑥,𝑦)<0。
当𝐹(𝑥𝑀,𝑦𝑀)<0时,取𝑃𝑢 (𝑥𝑖+1,𝑦𝑖 )
- 当𝐹(𝑥𝑀,𝑦𝑀 )>0时,取𝑃𝑑 (𝑥𝑖+1,𝑦𝑖−1)
- 当𝐹(𝑥𝑀,𝑦_𝑀 )=0时,约定取𝑃𝑢
算法步骤
- 输入圆的半径R;
- 计算初始值d=1.25-R、x=0、y=R;
- 绘制点(x,y)及其在八分圆中的另外七个对称点;
- 判断d的符号。若d≤0,则先将d更新为d+2x+3,再将(x,y)更新为(x+1,y);否则先将d更新为d+2(x-y)+5,再将(x,y)更新为(x+1,y-1);
-
改进
初始值为1.25-R,会导致出现小数运算,我们将d0=1.25-R改为1-R,则判别式d<=0改为d<=0.25,而由于始终取整数,则判别式可改为d<=0。
新的算法步骤为: 输入圆的半径R;
- 计算初始值d=1-R、x=0、y=R;
- 绘制点(x,y)及其在八分圆中的另外七个对称点;
- 判断d的符号。若d≤0,则先将d更新为d+2x+3,再将(x,y)更新为(x+1,y);否则先将d更新为d+2(x-y)+5,再将(x,y)更新为(x+1,y-1);
- 当x ≤
y时,重复步骤3和4。否则结束。
椭圆的扫描转换
原理
只对(2/Π,0)的四分之一圆进行绘制,其他部分通过对称得到。
构造函数,
- 对于椭圆上的点,有F(x,y)=0;
- 对于椭圆外的点,F(x,y)>0;
- 而对于椭圆内的点,F(x,y)<0。
算法原理:
- 从(0,b)到(a,0)顺时针地确定最佳逼近于第一象限椭圆弧的像素序列。
- 在上半部分, -1 ≤ k ≤0 , 最大位移方向为x;
- 在下半部分, k ≤-1 , 最大位移方向为y;
分别对上半部分和下半部分依次判断中点与椭圆边的关系,即:判别式的符号。
绘制
上半部分
判别式:
若di≤0,取P_u (x_i+1,y_i )
- 若di>0,取P_d (x_i+1,y_i-1)
下半部分
判别式:
- 若di≤0,取P_r (x_i+1,y_i-1)
- 若di>0,取P_l (x_i,y_i-1)
算法步骤
- 输入椭圆的长半轴a和短半轴b;
- 计算初始值:d=b2+a^2 (-b+0.25),x=0,y=b;
- 绘制点(x,y)及其在四分象限上的另外3个对称点;
- 判断d的符号。若d≤0,则先将d更新为d+b2(2x+3),再将(x,y)更新为(x+1,y);否则先将d更新为d+b2(2x+3)+a2(-2y+2),再将(x,y)更新为(x+1,y-1) ;
- 当b2(x+1)<a2(y-0.5)时,重复步骤(3)和(4),否则转(6);
- 用上半部分计算的最后点(x,y)来计算下半部分中d的初值:d=b^2(x+0.5)^2+a^2(y-1)^2-a2b2 ;
- 绘制点(x,y)及其在四分象限的另外3个对称点;
- 判断d的符号.若d<=0,则先将d更新为d+b2(2x+2)+a2(-2y+3),再将(x,y)更新为(x+1,y-1);否则先将d更新为d+a2(-2y+3),再将(x,y)更新为(x,y-1);
- 当y>=0时,重复步骤(7)和(8),否则结束。
多边形的扫描转换和区域填充
多边形的扫描转换
多边形的两种表示方法:
- 顶点表示
- 点阵表示
多边形的分类
- 确定多边形所占有的最大扫描线数,得到多边形顶点的最小和最大y值(ymin和ymax);
- 从y=ymin到y=ymax,每次用一条扫描线进行填充。对一条扫描线填充的过程可分为四个步骤:
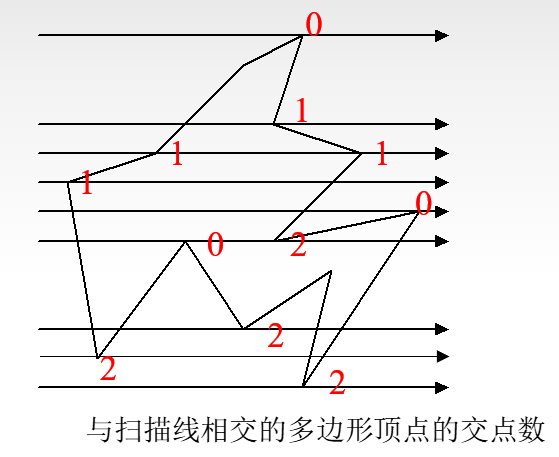
- 若共享顶点的两条边分别落在扫描线的两边,交点只算一个;
若共享顶点的两条边在扫描线的同一边,这时交点作为零个或两个;
- 具体解决方法为:检查共享顶点的两条边的另外两个端点的y值,按这两个y值中大于交点y值的个数是0、1、2来决定交点数取0、1、2。
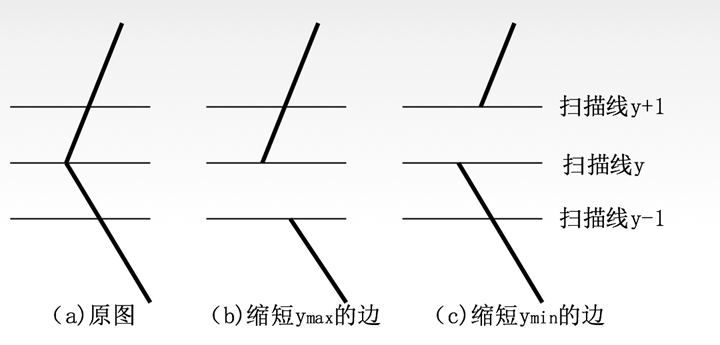
缺陷
改进的有效边表算法(也叫:y连贯性算法)
两个思想
- 第一个思想是扫描线的思想,当处理图形图像时按一条条扫描线处理;
-
原理简述
扫描线仅与多边形的有效边进行求交运算。
- 扫描线的连贯性。当前扫描线与边的交点顺序与下一根扫描线与边的交点顺序大概率一致,不必为下一条扫描线重新构建交点信息。
多边形的连贯性。某边与当前扫描线相交时,大概率也与下一条扫描线相交。
数据结构
有效边(Active Edge):指与当前扫描线相交的多边形的边,也称为活性边。
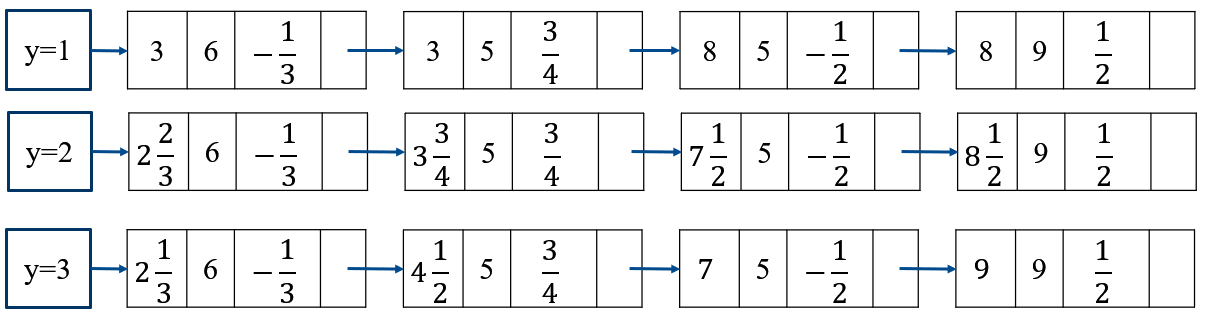
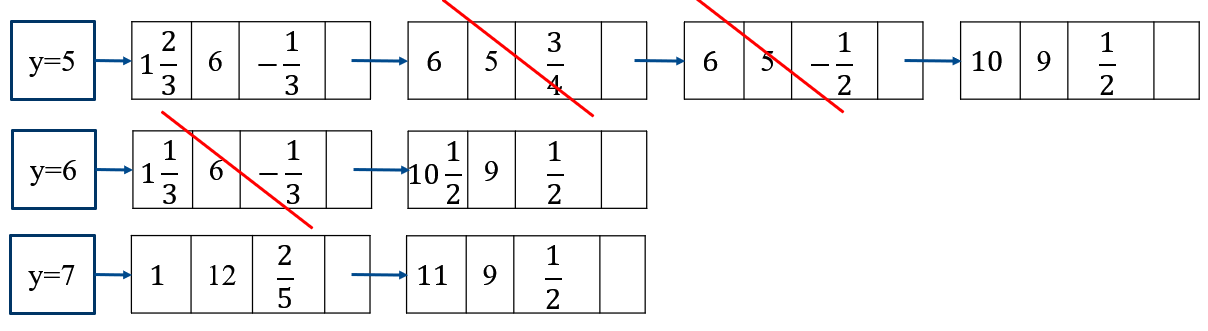
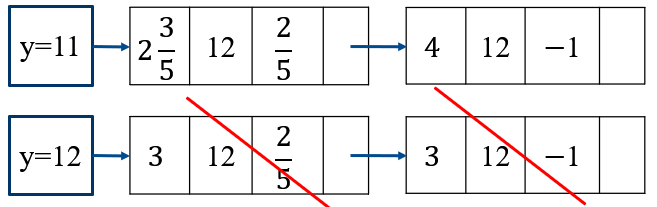
- 有效边表(Active Edge Table, AET):把有效边按与扫描线交点x坐标递增的顺序存放在一个链表中,此链表称为有效边表。
- 有效边表的每个结点:
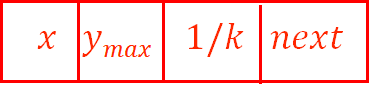
- x为当前扫描线与边的交点的x值
- ymax为边所在的最大扫描线值
- 1/k为从当前扫描线到下一条扫描线间x的增量
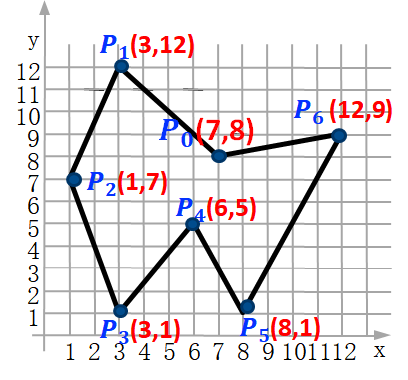
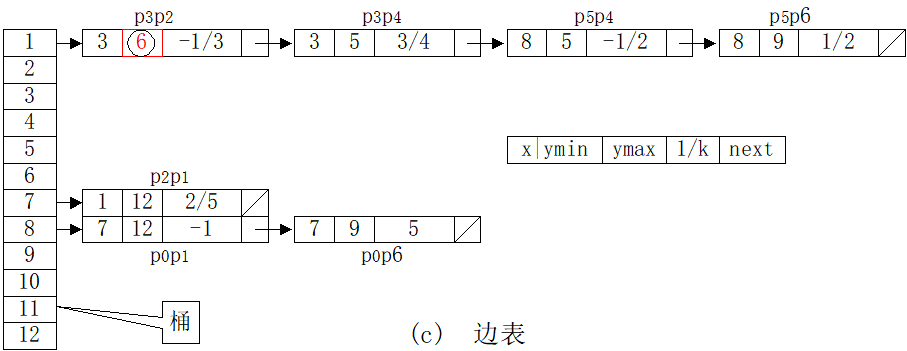
- 举例
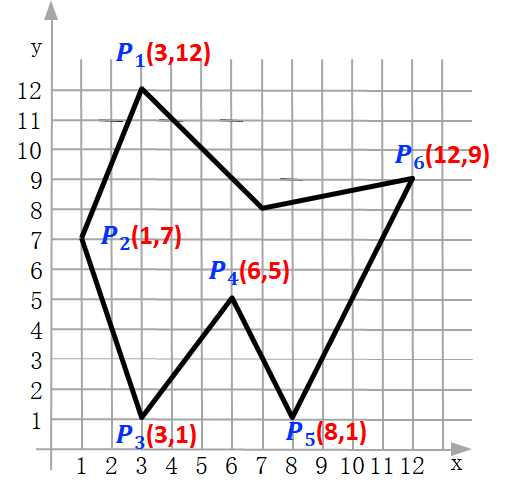
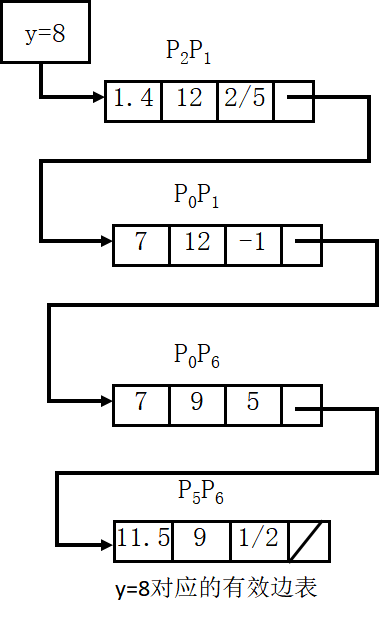
边表(Edge Table, ET):用来存放多边形的边的信息。
区域是指已经表示成点阵形式的填充图形,它是像素集合。
- 区域填充是指将区域内的一点(常称种子点)赋予给定颜色,然后将这种颜色扩展到整个区域内的过程。
- 区域的表示方法:
- 边界表示法:把位于给定区域的边界上像素一一列举出来的方法。
- 内点表示法:枚举出给定区域内所有像素的表示方法。
- 区域通常分为4-连通区域和8-连通区域两类。
- 栈顶像素出栈;
- 将出栈像素置成填充色;
- 检查出栈像素的4(8)-邻接点,若其中某个像素点不是边界色且未置成填充色,则把该像素入栈。
泛填充算法
算法的输入:种子点坐标(x,y),填充色和内部点原来的颜色。
算法原理:
算法从指定的种子(x,y)开始,用所希望的填充颜色赋给所有当前为给定内部颜色的像素点。
种子像素入栈;当栈非空时重复执行如下三步操作:
- 当以边界表示时,4-连通边界填充算法只能填充4-连通区域,8-连通边界填充算法也只能填充8-连通区域。
当以内点表示时,8-连通泛填充算法可以填充8-连通区域也可以填充4-连通区域,当然4-连通泛填充算法还是只能填充4-连通区域。
扫描转换和区域填充的区别
基本思想不同
- 多边形扫描转换是指将多边形的顶点表示转化为点阵表示;
- 区域填充只改变区域的填充颜色,不改变区域表示方法。
基于的条件不同
过取样(supersampling),或后滤波。
- 简单过取样:切割成更小的子像素。
- 重叠过取样:在对当前像素着色时同时对周围像素的子像素着色。
- 基于加权模板的过取样:确定像素亮度时按照对应的加权模板对中心点和四周点的子像素赋予不同的亮度。
- 区域取样(area
sampling),或前滤波。
- 简单区域采样:绘制有宽度的直线段时,根据所占像素面积的比例来赋予不同的灰度。
- 通过将每个像素亮度设置成与线条部分重叠的区域面积成正比,可以完成对直线的区域取样。即:若一个像素与线条部分重叠,根据重叠区域面积的大小来选择不同的灰度。重叠面积大的像素更黑一些,重叠面积小的像素更白一些。这种方法将产生模糊的边界,以此来减轻锯齿效应。
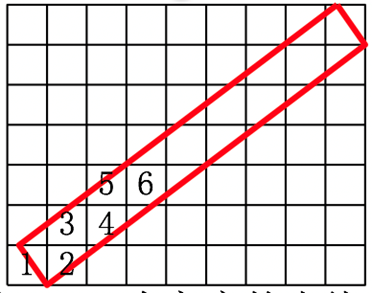
- 简单区域采样:绘制有宽度的直线段时,根据所占像素面积的比例来赋予不同的灰度。
6
- 为方便计算,可采用划分更小子像素的方式,以子像素的个数大致估计所占比。- 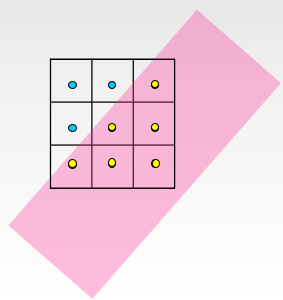
- 加权区域取样:假想一个连续的加权曲面(或过滤函数)覆盖像素。当直线条经过该像素时,该像素的灰度值是在二者重叠区域上对滤波器(过滤函数)进行积分的积分值。