2 表示 Representation

1. 信度Blief

命题比命题更可信：
当且仅当
当且仅当

2. 概率分布

概率分布：为不同的结果分配概率。分为离散和连续。

1. 离散概率分布

描述一组离散值的分布，表示为概率质量函数probability mass function
变量取值为个不同的值之一，使用冒号表示为
代表，代表
概率质量函数必须满足：，

1. 连续概率分布

描述一组连续值的分布，表示为概率密度函数probability density function
概率密度函数必须满足：
另一种表示连续分布的方法是使用累积分布函数cumulative distribution function
累计分布函数的定义：
分位数函数quantile function/逆累积分布函数inverse cumulative distribution function：是使得的值，即分位数函数返回累积分布值大于或等于的的最小值。

3. 联合分布

从联合分布中使用全概率公式计算边缘分布：或
使用决策树表示联合概率分布比使用表格的方法更紧凑。

4. 条件分布

条件概率：
贝叶斯规则：
条件高斯模型：假如有一个连续变量和一个值为离散变量，则定义为，参数向量。
线性高斯模型：的线性高斯模型将连续变量上的分布表示为一个高斯分布，其均值是连续变量的值的线性函数，条件密度函数为，参数。
条件线性高斯模型：结合了条件高斯模型和线性高斯模型的思想，能够处理连续变量对离散变量和连续变量的条件作用。假如和是连续变量，是值为的离散变量，条件密度函数为，参数向量。
贝叶斯网络：用来表示联合概率分布，结构是通过一个由节点和有向边组成的有向无环图来定义的，每个节点对应一个变量。有向边连接一对节点，图中不允许有环。有向边表示直接的概率关系。与每个节点相关联的是一个条件分布，其中表示的父节点。减少指定联合概率分布所需独立参数数量。
贝叶斯网络的链式法则：已知变量，计算所有这些变量对值的特定赋值的概率，其中是的父结点对其值的特定赋值。

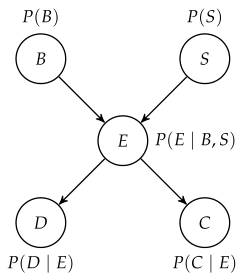
例如，下图为5个二进制变量的贝叶斯网络结构，所有变量的域都是，和没有任何父级，则所有变量都为的概率为

条件独立：当且仅当时，变量和在给定时是条件独立的，记作。当且仅当。给定，关于的信息不提供关于的其他信息，反之亦然。
d-分离(d-separation)：若满足以下任一条件，则与之间的一条路径被d-分离，是一组证据变量

• 路径包含节点链chain，且在中
• 路径包含叉fork，且在中
• 路径包含倒叉inverted fork，且不在中，的后代也不在中

如果和之间的所有路径都被d-分离，则和被d-分离，记作
马尔可夫覆盖(Markov blanket)：指节点的最小集合，如果其值已知，则使条件独立于所有其他节点。由其父节点、子节点和子节点的其他父节点组成。