7 精确解方法 Exact Solution Methods

:::info 首先描述马尔可夫决策过程模型，包括系统的随机动力学和与系统演化相关的效用。
使用不同的方法来计算效用，搜索最佳策略。在一定的假设下，可以得到MDP的精确解。 :::

1. 马尔可夫决策过程 MDP

MDP：元组
马尔可夫假设：下一状态仅取决于当前状态和动作，而不取决于任何先前状态或动作的假设。
MDP可以用决策网络表示（如下左图），效用函数被分解为收益 reward 。
平稳/stationary MDP：（如下右图）和不随时间变化。

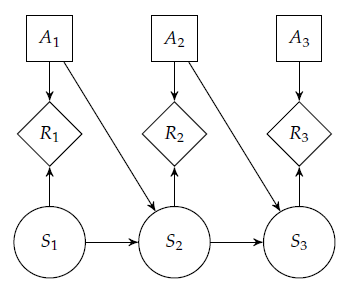
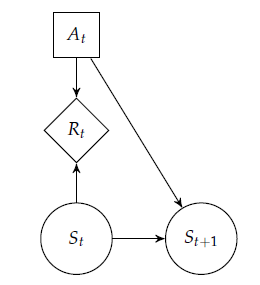
• 在包含步决策的finite horizon问题中，与奖励序列相关的效用（收益reward之和也称为回报 return）：
• 在infinite horizon问题中，避免使收益之和为无穷大：
  • 效用：，其中为折扣系数，当且收益有限，则效用值有限。
  • 平均回报：

：从状态执行的预期效用，通常被称为价值函数value function。
最优策略：使预期效用最大化的策略。
最优值函数：最优策略相关的价值函数。
使用动态规划计算最优策略更有效。

2. 策略评估 Policy Evaluation

策略评估 Policy Evaluation：计算价值函数

使用前向方程(lookahead)的后续步骤：
只要迭代次数足够，就能计算到任意精度。

通过矩阵形式求解方程组，则策略评估无需迭代：，其中，和分别是以向量形式表示的效用函数和回报函数。

求解的计算复杂度是。

总之，通过矩阵求逆实现精确计算，通过迭代算法实现近似计算。

3. 价值函数策略 Value Function Policies

:::info 上一节介绍如何计算与策略相关的价值函数，本节介绍如何从价值函数中提取策略。 ::: 贪婪策略 greedy policy：构造一个策略，使得前向方程最大化%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3C0%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%22573%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%22963%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221432%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%222099%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(3156%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6D%22%20x%3D%220%22%20y%3D%22NaN%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%22324%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(4156%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-28%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22792%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%221552%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%221941%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%222411%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%222856%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223385%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%223997%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B3%22%20x%3D%224998%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(5708%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(441%2C-1197)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2032%22%20x%3D%22578%22%20y%3D%22446%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-54%22%20x%3D%227319%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(8190%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2032%22%20x%3D%22663%22%20y%3D%22583%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2223%22%20x%3D%221431%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%221987%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%222457%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%222902%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223432%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-55%22%20x%3D%2212178%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(13112%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2032%22%20x%3D%22663%22%20y%3D%22583%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221153%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-29%22%20x%3D%2214656%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cpi%28s%29%3D%5Cunderset%7Ba%7D%7B%5Carg%20%5Cmax%20%7D%5Cleft%28R%28s%2C%20a%29%2B%5Cgamma%20%5Csum%7Bs%5E%7B%5Cprime%7D%7D%20T%5Cleft%28s%5E%7B%5Cprime%7D%20%5Cmid%20s%2C%20a%5Cright%29%20U%5Cleft%28s%5E%7B%5Cprime%7D%5Cright%29%5Cright%29&id=li7sZ)
动作价值函数action value function：也称为Q函数，表示从状态开始，执行动作，然后执行关于Q的贪婪策略时的预期回报
于是，价值函数为，策略为
优势函数advantage function：量化采取的动作与贪婪动作相比的优势

4. 策略迭代 Policy iteration

策略迭代Policy iteration：使用贪婪策略在策略评估和策略改进之间进行迭代。
但是，策略迭代的代价较高，因为必须在每次迭代中评估策略。

5. 价值迭代 Value iteration

价值迭代 Value iteration：策略迭代的一种替代方法，与策略改进不同，价值迭代直接更新价值函数。
通过贝尔曼更新Bellman backup/Bellman update改进价值函数：
重复此更新可以保证收敛到最优策略，最优策略满足贝尔曼最优方程Bellman optimality equation：
贝尔曼残差Bellman residual：，如果贝尔曼残差下降到阈值以下，则迭代终止。如果折扣因子接近，则收敛速度减慢，接近反之。

6. 异步价值迭代 Asynchronous Value Iteration

异步价值迭代 Asynchronous Value Iteration：每次迭代只更新状态的子集。
Gauss-Seidel价值迭代/value iteration：一种常见的异步价值迭代方法，扫描状态的顺序并应用贝尔曼更新，这种方法不必在每次迭代时在内存中构造第二个价值函数，节省计算量。比标准价值迭代收敛更快（取决于所选择的顺序）。

7. 线性规划公式 Linear Program Formulation

用一组不等式约束替换贝尔曼最优方程中的等式，并最小化每个状态下的：

用一组线性约束代替不等式中的最大化，变成线性规划：

在线性规划中，变量的数量为状态的数量，约束的数量为状态的数量乘以动作的数量。因为线性规划可以在多项式时间内求解，所以MDP也可以在多项式时间内求解。但在实践中，这种方法不如简单的价值迭代有效。

8. 二次收益的线性系统 Linear Systems with Quadratic Reward

在前面假设了离散状态空间和动作空间，这里假设连续的状态和动作，于是贝尔曼最优方程可以改为：

？