4 参数学习 Parameter Learning

:::info 本章讨论从数据中学习或拟合模型参数的问题。参数学习是指从数据中推断概率模型的参数。
首先介绍一种方法，在该方法中，确定模型的参数，以最大限度提高观察数据的可能性（最大似然）。并且，介绍了另一种贝叶斯方法，从未知参数上的概率分布开始，使用概率定律根据观测数据更新该分布。最后，我们讨论使用数据填充或期望最大化等方法来解决从缺失数据中学习参数的问题。 :::

1. 最大似然参数学习

在最大似然参数学习中，找到一个参数分布，使观测数据的可能性最大化。
如果表示一个分布的参数，则最大似然估计为
最大似然参数学习面临的挑战：

• 选择一个合适的概率模型来定义。通常假设数据的样本都是独立同分布，则样本来自分布，且
• 计算中的最大化，有些可能无法求出解析解。常见的方法是最大化对数似然，即

*注：本书表示以为底的对数。

1. Categorical分布的最大似然估计

对于二项分布：，其中表示总试验次数，表示出现其中某种情况的次数。
对数似然相当于：
最大化对数似然，可以通过求一阶导：，则，即
假如有种不同的值，则的最大似然估计值是：

1. 高斯分布的最大似然估计

个样本，与上述步骤一致：

1. 贝叶斯网络的最大似然估计

？

2. 贝叶斯参数学习

与最大似然估计获得参数的点估计不同，贝叶斯参数学习获得的是分布。
可以通过计算期望值将此分布转换为点估计：
或者使用最大后验估计：，该估计值对应于分配了最大密度的值
贝叶斯参数学习可以视为具有如下贝叶斯网络结构中的推断，假设观测变量相互独立。已知先验，接下来讨论如何将贝叶斯参数学习应用于的不同模型。

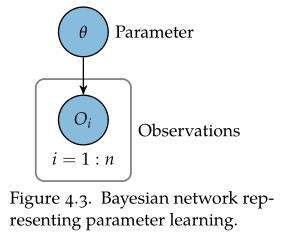
1. 二项分布的贝叶斯学习

假设在二项分布中学习参数，，需要学习的分布。
使用之前的方法进行推断：
，其中是的次数
为了找到归一化常数：，其中伽马函数
归一化之后：
即服从beta分布：

如果二项分布的参数的先验分布是beta分布，则后验分布也是beta分布。
如果先验是，且得到一个观测值（和参数有时被称为伪计数pseudocount）：

• 若，则获得后验
• 若，则获得后验

从先验开始，获得的观测值是次飞行中有次碰撞，则后验是
对于先验的选择，原则上应在不知道用于计算后验的数据的情况下选择统一的先验。但如果有专家知识，则可以将其编码到先验中。
一般来说，先验的重要性随着用于计算后验的数据量的增加而降低。

1. Categorical分布的贝叶斯学习

Dirichlet分布是beta分布的推广，可用于估计categorical分布的参数。
假设是一个离散的随机变量，其整数值从到，定义categorical分布的参数为，且。
Dirichlet分布可用于表示先验分布和后验分布，参数是，表示为：，其中表示参数的总和。如果，则该式等效于beta分布。
如果上的先验值由给出，并且存在的个观测值，则后验值为：

1. 贝叶斯网络的贝叶斯学习

贝叶斯网络参数的先验
？

3. 非参数学习 Nonparametric Learning

前面假设概率模型为固定形式，并从数据中学习固定的参数集。而另一种方法是基于非参数方法，其中参数的数量随数据量而变化。一种常见的非参数方法是核密度估计。
给定观测值，核密度估计表示的密度。其中是积分为的核函数，用于为观测数据点附近的值分配更大的密度。
一个常见的核是零均值高斯分布。当使用这样的核时，标准差通常被称为带宽，可以调整带宽来控制密度函数的平滑度。带宽越大，密度越平滑。贝叶斯方法可用于根据数据选择适当的带宽。

4. 使用缺失数据进行学习

使用缺失数据进行学习是大量文献的主题。
处理缺失数据的一种方法是丢弃所有有一个或多个缺失条目的、不完整的实例，但会造成数据的浪费。
可以使用最大似然法或贝叶斯方法从缺失数据中学习模型参数。如果采用贝叶斯最大后验方法，我们希望得到估计值：，其中，和分别由所有观测数据和缺失数据组成。但是，对缺失数据的进行边缘化可能是计算困难的。
注：如果数据是连续的，那么被所代替。
这里只关注数据随机缺失的情况，即在给定观察变量值的情况下，条目缺失的概率条件独立于其值。本节讨论使用缺失数据进行学习的两种通用方法：① 使用缺失条目的预测值来学习分布参数；② *改进参数估计的迭代方法。

1. 数据填充 Data imputation

放弃不完整实例的另一种方法是填充缺失条目的值，数据填充是为缺失条目推断值的过程。

于是，使用该填充的数据近似产生最大后验估计：
但是，式①在计算上具有挑战性。对于离散数据集，一种简单方法是用最常见的观测值替换缺失的条目（称为marginal mode），但这种填充方法不总是产生合理的预测。还有种方法是最近邻插补nearest-neighbor imputation，使用与观察变量定义的距离度量最接近的实例相关的值，该方法的填充效果更好。另一种方法是将分布拟合到完全观测的数据，然后使用该分布推断缺失值（使用前一章中的推断算法来执行此推断）。

1. 期望最大化Expectation-Maximization

期望最大化（EM）方法进行对分布参数估计的迭代改进。

• STEP 1：期望步骤（E步骤）。使用的当前估计来推断数据的完整性。在有缺失变量的情况下，可以使用基于采样的方法。
• STEP 2：最大化步骤（M步骤）。试图得到一个新的，以最大化完整数据的可能性。