密码学概述

密码学是指研究信息加密，破解密码的技术科学。密码学的起源可追溯到2000年前。而当今的密码学是以数学为基础的。

发展历史

密码学的历史大致可以追溯到两千年前，相传古罗马名将凯撒大帝为了防止敌方截获情报，用密码传送情报。凯撒的做法很简单，就是对二十几个罗马字母建立一张对应表。这样，如果不知道密码本，即使截获一段信息也看不懂

凯撒密码（Caesar cipher）：

从凯撒大帝时代到上世纪70年代这段很长的时间里，密码学的发展非常的缓慢，因为设计者基本上靠经验，没有运用数学原理

这种加密方式的弊端

• 密码本泄露，密码将被破解
• 获取足够多的情报，通过大数据分析，统计字母出现频率，也能找到其中的规则

---

在1976年以前，所有的加密方法都是同一种模式：加密、解密使用同一种算法。在交互数据的时候，彼此通信的双方就必须将规则告诉对方，否则没法解密。那么加密和解密的规则（简称密钥），它保护就显得尤其重要。传递密钥就成为了最大的隐患。这种加密方式被成为对称加密算法（symmetric encryption algorithm）

1976年，两位美国计算机学家迪菲（W.Diffie）、赫尔曼（M.Hellman） 提出了一种崭新构思，可以在不直接传递密钥的情况下，完成密钥交换。这被称为“迪菲赫尔曼密钥交换”算法。开创了密码学研究的新方向

1977年，三位麻省理工学院的数学家罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起设计了一种算法，可以实现非对称加密。这个算法用他们三个人的名字命名，叫做RSA算法

RSA数学原理

上世纪70年代产生的一种加密算法。其加密方式比较特殊，需要两个密钥：公开密钥简称公钥（publickey）和私有密钥简称私钥（privatekey）。公钥加密，私钥解密；私钥加密，公钥解密。这个加密算法就是伟大的RSA

取模算法

通过数学进行加密，必须满足一个算法，加密容易，但通过加密结果反算原始内容一定要很难

早期的取模算法，在西方称为时钟算数

• 环，即：取模，或者可将取模运算理解是环上的运算
• 环即是取模，也是周期，取模即是周期

质数

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数。规定1既不是质数也不是合数

质数2，是一个特殊的质数

• 是最小的质数
• 是质数中唯一的偶数
• 是偶数中唯一的质数
• 假如两个或偶数个质数之和为奇数，则其中必定有一个是2
• 假如两个或偶数个质数只差为奇数，则其中必定有一个是2
• 假如三个或奇数个质数之和为偶数，则其中必定有一个是2
• 假如三个或奇数个质数之差为偶数，则其中必定有一个是2
• 假如若干个质数之积为偶数，则其中必定有一个是2

原根

原根是一种数学符号，设n是正整数，m是整数，若m模n的阶等于φ(n)，则称m为模n的一个原根

原根存在的条件有以下几个：

• 设n是奇质数，则模n的原根存在
• 设m是模n的原根，则m或m + n是模n ^ 2的原根
• 设n是奇质数，则对任意e，模n ^ e的原根存在
• 设e >= 1，若m是模n ^ e的一个原根，则m与m + n ^ e中的奇数是模2 * n ^ e的一个原根

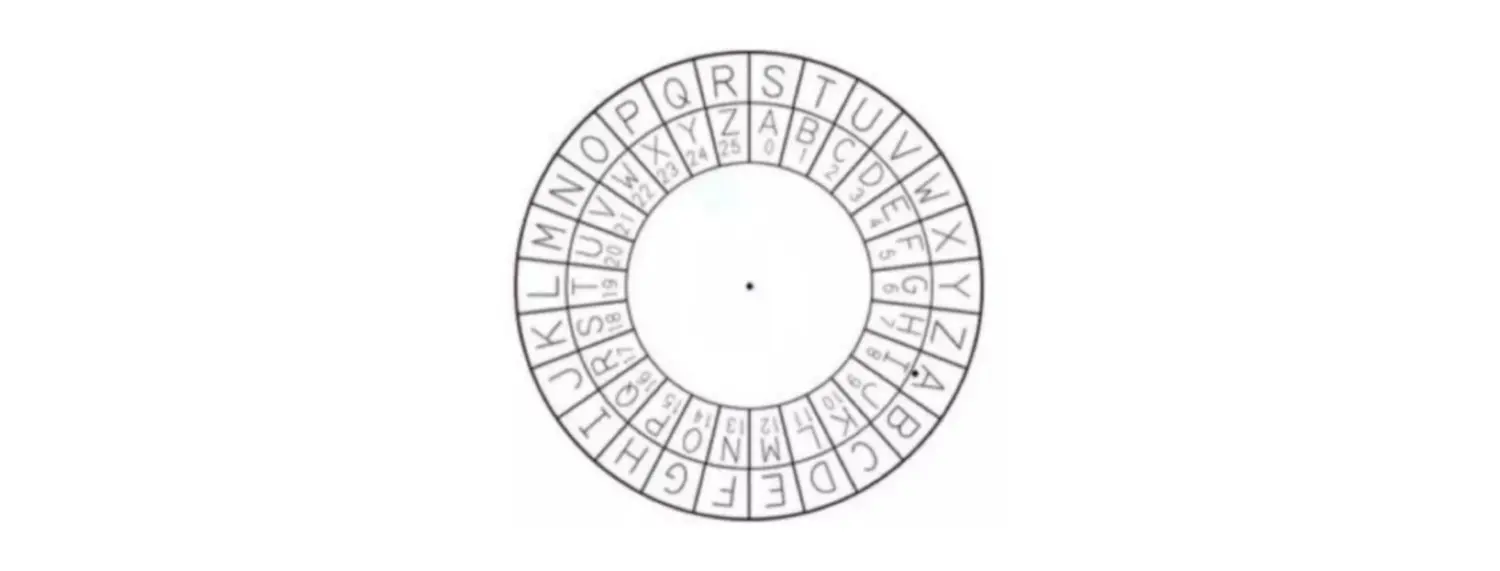
例如：使用质数17作为模数，再使用一个比17小的质数3模以17

3 % 17，此时3的1-16次方模以17，得到的如下结果：

• 3的1-16次方，模拟17的结果都不一样。
• 3的17次方，模以17的结果为3，和3的1次方模以17的结果一样。3的18次方和2次方的结果一样…

上述规律，称之为3是17的原根

离散对数问题

如果使用上述规律作为算法，3的x次方的结果，一定是1-16之间的数字，但是通过结果反算x很难

当模数的质数越大，反算的难度就会越大，这种情况被称之为离散对数问题

欧拉函数φ

互质关系：如果两个正整数，除了1以外，没有其他公因数，我们就称这两个数是互质关系（coprime）

任意给定正整数n，在小于等于n的正整数之中，有多少个数可以与n构成互质关系？

计算这个值的公式叫做欧拉函数，使用：φ(n)表示

---

案例1:

计算8的欧拉函数，和8互质的1、2、3、4、5、6、7、8
φ(8) = 4

---

案例2:

计算7的欧拉函数，和7互质的1、2、3、4、5、6、7
φ(7) = 6

---

欧拉函数特点：

当n是质数的时候，φ(n) = n - 1

如果n可以分解成两个互质的整数之积

• n = p1 * p2
• φ(p1 * p2) = φ(p1) * φ(p2)

根据以上两点得到：

• 如果n是两个质数p1和p2的乘积，且p1和p2互质
• φ(n) = φ(p1) * φ(p2) = (p1 - 1) * (p2 - 1)

---

案例3:

计算56的欧拉函数
φ(56) = φ(8) * φ(7) = 4 * 6 = 24

欧拉定理

• 如果两个正整数m和n互质，那么m的φ(n)次方减去1，可以被n整除
• m ^ φ(n) - 1 % n ≡ 0 ↓
• m ^ φ(n) % n ≡ 1

例如：m = 5，n = 8，φ(8) = 4

5 ** 4 % 8
-------------------------
1

费马小定理

• 欧拉定理的特殊情况：如果两个正整数m和n互质，而且n为质数
• φ(n)结果就是n - 1
• m ^ (n - 1) % n ≡ 1

例如：m = 6，n = 5

6 ** (5 - 1) % 5
-------------------------
1

公式转换

① 费马小定理

• m ^ φ(n) % n ≡ 1

---

② 由于1 ^ k ≡ 1

• 将m ^ φ(n) % n看作一个整体x
• x ≡ m ^ φ(n) % n ≡ 1 ↓
• x ^ k ≡ 1 ^ k

当m和n互质

• x ^ k ≡ m ^ (k * φ(n)) % n ↓
• m ^ (k * φ(n)) % n ≡ 1

例如：m = 6，n = 5，k = 3

6 ** (3 * (5 - 1) ) % 5
-------------------------
1

---

③ 由于1 * m ≡ m

• m ^ (k * φ(n) + 1) % n ≡ m

例如：m = 6，n = 7，k = 3

6 ** (3 * (7 - 1) + 1) % 7
-------------------------
6

• 注：必须m小于n，此公式才成立

模反元素

④ 如果两个正整数e和x互质，那么一定可以找到整数d，使得ed - 1被x整除。d就是e对于x的“模反元素”

• e * d - 1 % x ≡ 0 ↓
• e * d % x ≡ 1

---

⑤ 由公式④推导

• e * d - 1 % x ≡ 0 ↓
• e * d - 1 / x ≡ k ↓
• e * d - 1 ≡ k * x ↓
• e * d ≡ k * x + 1

---

⑥ 由公式③推导，如果x = φ(n)：

• m ^ (k * φ(n) + 1) % n ≡ m ↓
• m ^ (k * x + 1) % n ≡ m

由公式⑤推导，e和x（φ(n)）互质，得到以下公式：

• e * d ≡ k * x + 1 ↓
• m ^ (e * d) % n ≡ m

---

案例：

m = 4，n = 15，当x的值等于φ(n)

• x = φ(n) = φ(15) = φ(3) * φ(5) = 2 * 4 = 8
• e和x互质，e = 3
• e * d - 1 / x ≡ k ↓
• e * d - 1 = x * k ↓
• d = (x * k + 1) / e

计算d的值

• k = 4，(8 * 4 + 1) / 3，d = 11
• k = 7，(8 * 7 + 1) / 3，d = 19

d = 11，代入公式：m ^ (e * d) % n ≡ m

4 ** (3 * 11) % 15
-------------------------
4

d = 19，代入公式：m ^ (e * d) % n ≡ m

4 ** (3 * 19) % 15
-------------------------
4

迪菲赫尔曼密钥交换

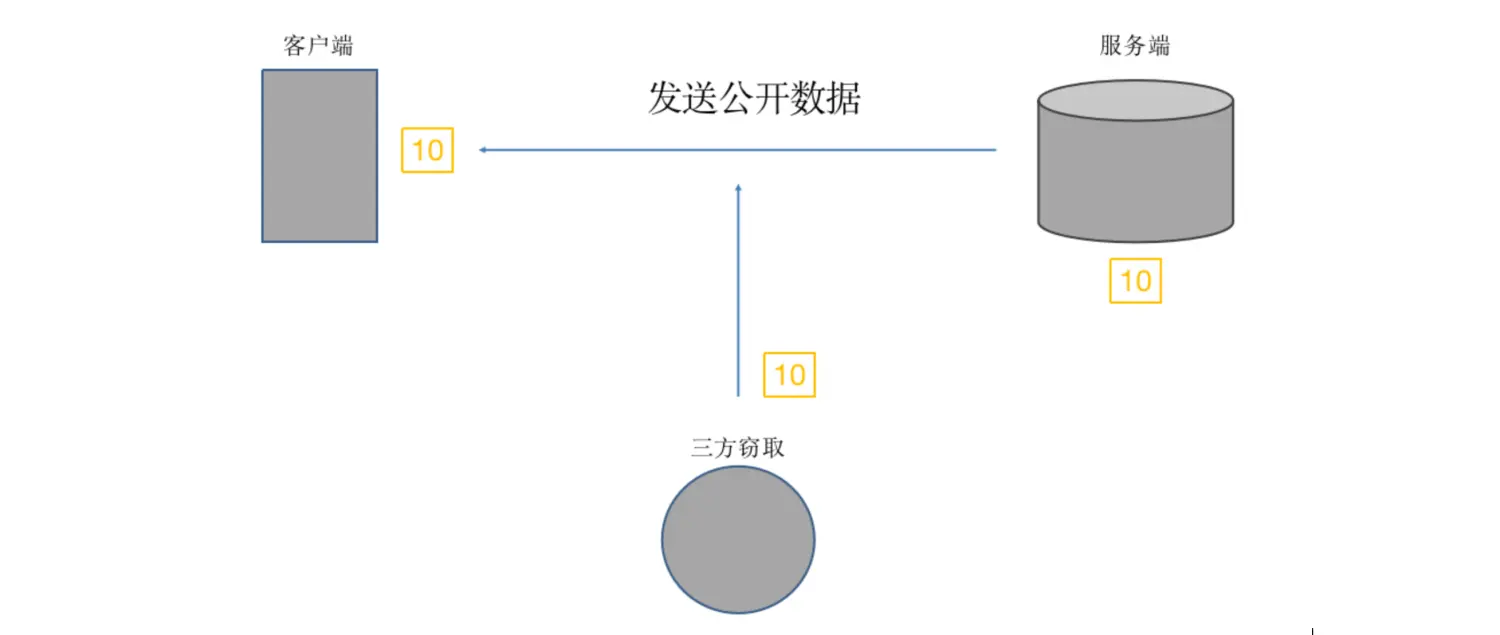
迪菲赫尔曼密钥交换是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容

使用对称加密，假设10为密钥

• 服务端与客户端加解密，需要服务端传递密钥给客户端。如果密钥被第三方窃取，加密则不再安全

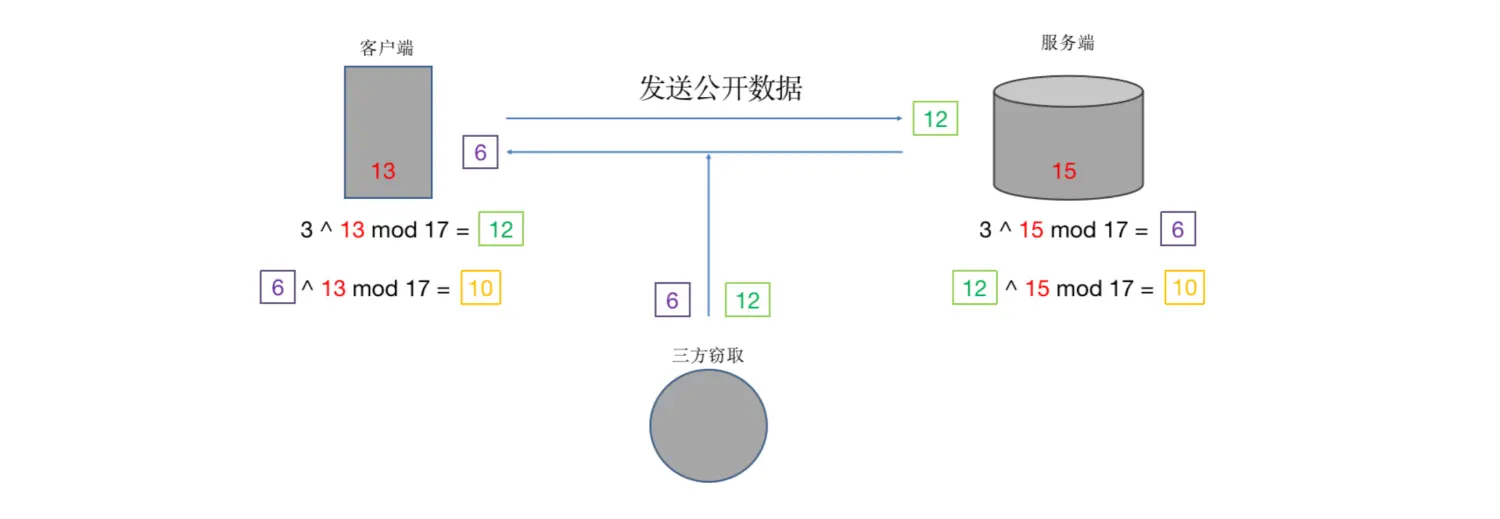
使用迪菲赫尔曼密钥交换，假设一个传递密钥的场景，算法是3的n次方模以17

• 服务端和客户端，分别通过算法计算出两个随机数，15和13
• 两端使用相同的算法，计算出6和12
• 两端将结果6和12传递给对方
• 两端再次使用相同的算法，都计算出结果10
• 案例中，10才是对称加密真正使用的密钥。在数据传输中，第三方只能窃取到6和12两个数字。即便知道算法，再得不到15和13的情况下，也无法计算出密钥

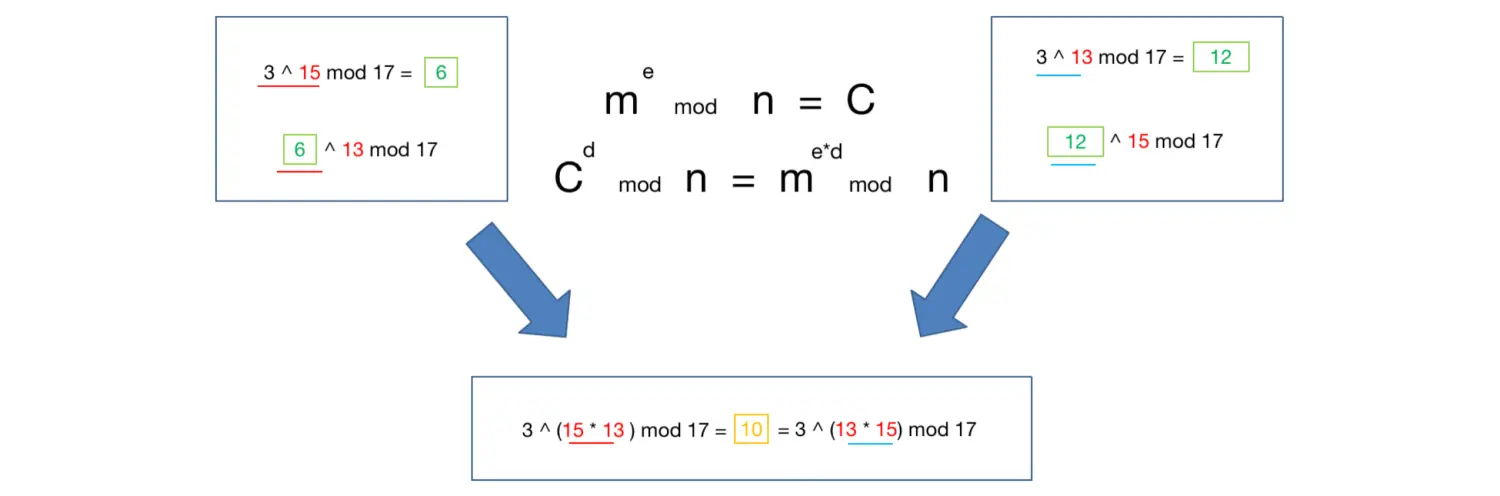
迪菲赫尔曼密钥交换公式原理：

• 公式成立的条件在于，3是17的原根
• 公式3 ^ (13 * 15) % 17就是模反元素公式⑥的m ^ (e * d) % n ≡ m，相当于将其拆分成两步

RSA算法

RSA公开密钥密码体制的原理是：根据数论，寻求两个大质数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥

• n会非常大，长度一般为1024个二进制位。目前人类已经分解的最大整数，232个十进制位，768个二进制位
• 由于需要求出φ(n)，所以根据欧函数特点，最简单的方式n由两个质数相乘得到。质数：p1、p2
φ(n) = (p1 - 1) * (p2 - 1)
• 最终由φ(n)得到e和d

总共生成6个数字：p1、p2、n、φ(n)、e、d

• 公钥：n和e
• 私钥：n和d
• 明文：m
• 密文：c

---

案例：

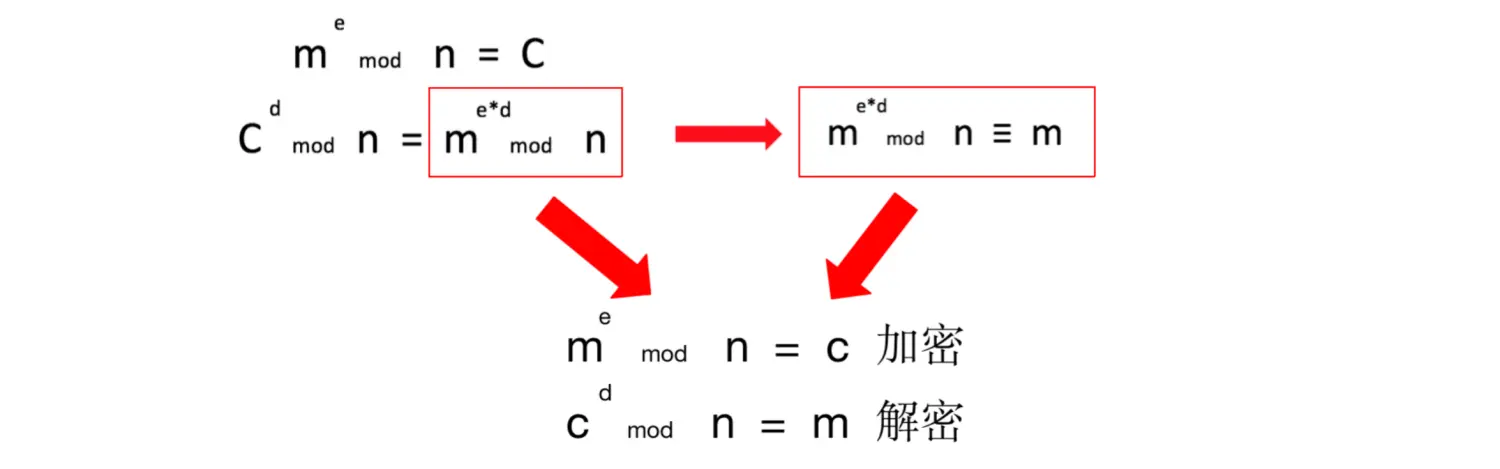
m = 12，n = 15，φ(n) = 8，e = 3，d = 11

加密：m ^ e % n = c

12 ** 3 % 15
-------------------------
3

解密：c ^ d % n = m

3 ** 11 % 15
-------------------------
12

---

RSA的安全：

• 除了公钥用到了n和e，其余的4个数字是不公开的

目前破解RSA得到d的方式如下：

• 要想求出私钥d，由于e * d = φ(n) * k + 1。需要知道e和φ(n)
• e是知道的，但是要得到φ(n)，就必须知道p1和p2
• 由于n = p1 * p2。只有将n因数分解才能算出

---

运算速度

• 由于进行的都是大数计算，使得RSA最快的情况也比DES慢上好几倍
• RSA的速度比对应同样安全级别的对称密码算法要慢1000倍左右
• 速度一直是RSA的缺陷，所以大量数据并不适合RSA，一般来说只用于少量数据加密
• 日常开发中，大数据采用对称加密，例如：DES。而对称加密使用的密钥，则通过RSA进行加密

终端命令

Mac的终端可以直接使用OpenSSL进行RSA的命令运行。

OpenSSL

由于Mac系统内置开源加密库OpenSSL，所以在终端上可以直接使用命令运行RSA，OpenSSL中RSA算法常用指令主要有三个：

命令	含义
genrsa	生成并输入一个RSA私钥
result	使用RSA密钥进行加密、解密、签名和验证等运算
rsa	处理RSA密钥的格式转换等问题

案例1：

生成RSA私钥，密钥长度为1024bit

openssl genrsa -out private.pem 1024
-------------------------
Generating RSA private key, 1024 bit long modulus (2 primes)
...........+++++
..+++++
e is 65537 (0x010001)

从私钥中提取公钥

openssl rsa -in private.pem -pubout -out public.pem
-------------------------
writing RSA key

生成私钥和公钥的证书文件

使用cat private.pem命令，查看private.pem内容

-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQCzxKp3IKq2SHTqJXgZ0aU0lCHJl/f6VWZs5PXsB26yoe6kwqDN
HJWba8hPY7eewAq9/HUyH1MhQUUKwOj8+etwrdfwd0aPwYsRdtT2QzC2LRT1y43A
+IUR0uUbGE1kMROPheyWcBmTA/zcXAINKhGF/Z/pUCzouoUbNh950VHfQQIDAQAB
AoGASMhpVA4Pz/mKDHrbI2j0AFOxUlOK/PmynIge4U8pDH3vhxmdzS2zjNeYpDv1
Tfrm3oDmWkLAf4hTkcUFD9eH8MsNsnORUnn+PbHGIysrArDdwbOtj4LE66YHfQxN
lf/Gi4Zpao4p5wBcsiZYaOWtor5oUsLOf1kKlIqt5/8szZkCQQDjmpVebA34lZFj
7dqXqZsYEB4HWHOnbtnV12UM77BqzPoAZjapAEa2Ofn/ct3RIqvXWrmY3pH6PiQQ
KJUk1+DfAkEAyjJD8vBoUiWH8ktNmHE5ua/H1Vmk6to5MenjKRNj9ACB/BvopfaS
xSr2PuVeQU9AOZNEGduadxaTOLJPCsmj3wJAdJ+n++roOcEB769X+7B3fRv9Fwx2
rot5aT5mU/uZbRA85el6BpzSntsUQ5VrHZdjcATX5wHc0Nn4hqMU0P0hBwJBAJC7
6me8LvCebPHDdYfphKimayUNRj/WdZqFEVYVyzaeJm2QjLhACE+asSnUheO6Fv8f
q1/XEnqsbjXnbS0LqYECQQCi+amvIpqvCUJeFDM9A9noPTEkAHWClBuCmBCeHl8+
RJdYx9ZJj3w81013xir06pX3YTKQvbzWpEUcNMBPl4N/
-----END RSA PRIVATE KEY-----

• 二进制文件，以Base64编码格式展示，占887字节

使用cat public.pem命令，查看public.pem内容

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCzxKp3IKq2SHTqJXgZ0aU0lCHJ
l/f6VWZs5PXsB26yoe6kwqDNHJWba8hPY7eewAq9/HUyH1MhQUUKwOj8+etwrdfw
d0aPwYsRdtT2QzC2LRT1y43A+IUR0uUbGE1kMROPheyWcBmTA/zcXAINKhGF/Z/p
UCzouoUbNh950VHfQQIDAQAB
-----END PUBLIC KEY-----

• 二进制文件，以Base64编码格式展示，占272字节
• 公钥比私钥小很多

案例2：

创建message.txt文件，写入以下内容：

ha ha ha ~

通过公钥加密

openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enc.txt

使用cat enc.txt命令，查看加密内容

• enc.txt为二进制文件，显示乱码

通过私钥加密

openssl rsautl -decrypt -in enc.txt -inkey private.pem -out dec.txt

使用cat dec.txt命令，查看解密内容

ha ha ha ~

• 原文11字节，密文128字节，使用RSA加密，数据增大很多

案例3：

通过私钥签名

openssl rsautl -sign -in message.txt -inkey private.pem -out enc.txt

使用cat enc.txt命令，查看加密内容

• 二进制文件， 无法直接查看

通过公钥验证

openssl rsautl -verify -in enc.txt -inkey public.pem -pubin -out dec.txt

使用cat dec.txt命令，查看解密内容

ha ha ha ~

案例4：

将私钥转换成为明文

openssl rsa -in private.pem -text -out private.txt
-------------------------
writing RSA key

使用cat private.txt命令，查看明文内容

RSA Private-Key: (1024 bit, 2 primes)
modulus:
   00:b3:c4:aa:77:20:aa:b6:48:74:ea:25:78:19:d1:
   a5:34:94:21:c9:97:f7:fa:55:66:6c:e4:f5:ec:07:
   6e:b2:a1:ee:a4:c2:a0:cd:1c:95:9b:6b:c8:4f:63:
   b7:9e:c0:0a:bd:fc:75:32:1f:53:21:41:45:0a:c0:
   e8:fc:f9:eb:70:ad:d7:f0:77:46:8f:c1:8b:11:76:
   d4:f6:43:30:b6:2d:14:f5:cb:8d:c0:f8:85:11:d2:
   e5:1b:18:4d:64:31:13:8f:85:ec:96:70:19:93:03:
   fc:dc:5c:02:0d:2a:11:85:fd:9f:e9:50:2c:e8:ba:
   85:1b:36:1f:79:d1:51:df:41
publicExponent: 65537 (0x10001)
privateExponent:
   48:c8:69:54:0e:0f:cf:f9:8a:0c:7a:db:23:68:f4:
   00:53:b1:52:53:8a:fc:f9:b2:9c:88:1e:e1:4f:29:
   0c:7d:ef:87:19:9d:cd:2d:b3:8c:d7:98:a4:3b:f5:
   4d:fa:e6:de:80:e6:5a:42:c0:7f:88:53:91:c5:05:
   0f:d7:87:f0:cb:0d:b2:73:91:52:79:fe:3d:b1:c6:
   23:2b:2b:02:b0:dd:c1:b3:ad:8f:82:c4:eb:a6:07:
   7d:0c:4d:95:ff:c6:8b:86:69:6a:8e:29:e7:00:5c:
   b2:26:58:68:e5:ad:a2:be:68:52:c2:ce:7f:59:0a:
   94:8a:ad:e7:ff:2c:cd:99
prime1:
   00:e3:9a:95:5e:6c:0d:f8:95:91:63:ed:da:97:a9:
   9b:18:10:1e:07:58:73:a7:6e:d9:d5:d7:65:0c:ef:
   b0:6a:cc:fa:00:66:36:a9:00:46:b6:39:f9:ff:72:
   dd:d1:22:ab:d7:5a:b9:98:de:91:fa:3e:24:10:28:
   95:24:d7:e0:df
prime2:
   00:ca:32:43:f2:f0:68:52:25:87:f2:4b:4d:98:71:
   39:b9:af:c7:d5:59:a4:ea:da:39:31:e9:e3:29:13:
   63:f4:00:81:fc:1b:e8:a5:f6:92:c5:2a:f6:3e:e5:
   5e:41:4f:40:39:93:44:19:db:9a:77:16:93:38:b2:
   4f:0a:c9:a3:df
exponent1:
   74:9f:a7:fb:ea:e8:39:c1:01:ef:af:57:fb:b0:77:
   7d:1b:fd:17:0c:76:ae:8b:79:69:3e:66:53:fb:99:
   6d:10:3c:e5:e9:7a:06:9c:d2:9e:db:14:43:95:6b:
   1d:97:63:70:04:d7:e7:01:dc:d0:d9:f8:86:a3:14:
   d0:fd:21:07
exponent2:
   00:90:bb:ea:67:bc:2e:f0:9e:6c:f1:c3:75:87:e9:
   84:a8:a6:6b:25:0d:46:3f:d6:75:9a:85:11:56:15:
   cb:36:9e:26:6d:90:8c:b8:40:08:4f:9a:b1:29:d4:
   85:e3:ba:16:ff:1f:ab:5f:d7:12:7a:ac:6e:35:e7:
   6d:2d:0b:a9:81
coefficient:
   00:a2:f9:a9:af:22:9a:af:09:42:5e:14:33:3d:03:
   d9:e8:3d:31:24:00:75:82:94:1b:82:98:10:9e:1e:
   5f:3e:44:97:58:c7:d6:49:8f:7c:3c:d7:4d:77:c6:
   2a:f4:ea:95:f7:61:32:90:bd:bc:d6:a4:45:1c:34:
   c0:4f:97:83:7f
-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQCzxKp3IKq2SHTqJXgZ0aU0lCHJl/f6VWZs5PXsB26yoe6kwqDN
HJWba8hPY7eewAq9/HUyH1MhQUUKwOj8+etwrdfwd0aPwYsRdtT2QzC2LRT1y43A
+IUR0uUbGE1kMROPheyWcBmTA/zcXAINKhGF/Z/pUCzouoUbNh950VHfQQIDAQAB
AoGASMhpVA4Pz/mKDHrbI2j0AFOxUlOK/PmynIge4U8pDH3vhxmdzS2zjNeYpDv1
Tfrm3oDmWkLAf4hTkcUFD9eH8MsNsnORUnn+PbHGIysrArDdwbOtj4LE66YHfQxN
lf/Gi4Zpao4p5wBcsiZYaOWtor5oUsLOf1kKlIqt5/8szZkCQQDjmpVebA34lZFj
7dqXqZsYEB4HWHOnbtnV12UM77BqzPoAZjapAEa2Ofn/ct3RIqvXWrmY3pH6PiQQ
KJUk1+DfAkEAyjJD8vBoUiWH8ktNmHE5ua/H1Vmk6to5MenjKRNj9ACB/BvopfaS
xSr2PuVeQU9AOZNEGduadxaTOLJPCsmj3wJAdJ+n++roOcEB769X+7B3fRv9Fwx2
rot5aT5mU/uZbRA85el6BpzSntsUQ5VrHZdjcATX5wHc0Nn4hqMU0P0hBwJBAJC7
6me8LvCebPHDdYfphKimayUNRj/WdZqFEVYVyzaeJm2QjLhACE+asSnUheO6Fv8f
q1/XEnqsbjXnbS0LqYECQQCi+amvIpqvCUJeFDM9A9noPTEkAHWClBuCmBCeHl8+
RJdYx9ZJj3w81013xir06pX3YTKQvbzWpEUcNMBPl4N/
-----END RSA PRIVATE KEY-----

• 上面是二进制数据，最后面的是私钥
• 其中publicExponent: 65537 (0x10001)就是e
• 公钥和e，在私钥中已经存在。公钥是通过私钥计算得到的

代码演示

RSA代码加解密，iOS无法直接使用.pem证书，需要使用p12和der

案例1：

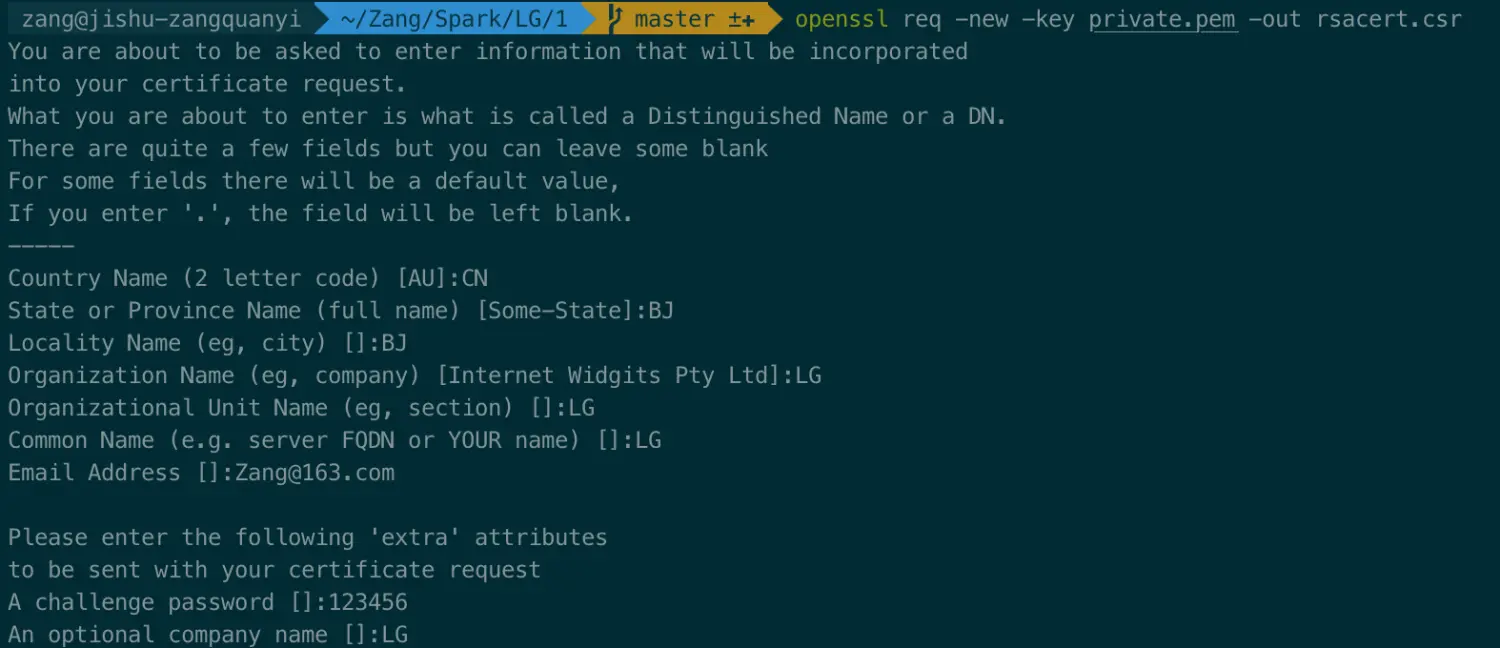
通过私钥生成.csr请求文件

openssl req -new -key private.pem -out rsacert.csr

• 按提示输入信息

目录下生成rsacert.csr文件

• 通过私钥生成.csr请求文件，将其发给颁发证书的机构进行签名，证明此证书的合法性。例如：https使用的ssl证书

案例2：

对.csr文件自签名，生成.crt证书

openssl x509 -req -days 3650 -in rsacert.csr -signkey private.pem -out rsacert.crt
-------------------------
Signature ok
subject=C = CN, ST = BJ, L = BJ, O = LG, OU = LG, CN = LG, emailAddress = Zang@163.com
Getting Private key

• 自签名证书是未经认证的，不受各类浏览器信任。仅用来案例演示，自娱自乐

目录下生成rsacert.crt证书文件

• 例如：使用https协议，需要将.crt证书放在服务器上，供客户端接收

使用cat rsacert.crt命令，查看证书内容

-----BEGIN CERTIFICATE-----
MIICWDCCAcECFGuo1neUJVorMs1aHTn7m+JM79dwMA0GCSqGSIb3DQEBCwUAMGsx
CzAJBgNVBAYTAkNOMQswCQYDVQQIDAJCSjELMAkGA1UEBwwCQkoxCzAJBgNVBAoM
AkxHMQswCQYDVQQLDAJMRzELMAkGA1UEAwwCTEcxGzAZBgkqhkiG9w0BCQEWDFph
bmdAMTYzLmNvbTAeFw0yMTA0MTMxMDM5MTNaFw0zMTA0MTExMDM5MTNaMGsxCzAJ
BgNVBAYTAkNOMQswCQYDVQQIDAJCSjELMAkGA1UEBwwCQkoxCzAJBgNVBAoMAkxH
MQswCQYDVQQLDAJMRzELMAkGA1UEAwwCTEcxGzAZBgkqhkiG9w0BCQEWDFphbmdA
MTYzLmNvbTCBnzANBgkqhkiG9w0BAQEFAAOBjQAwgYkCgYEAs8SqdyCqtkh06iV4
GdGlNJQhyZf3+lVmbOT17AdusqHupMKgzRyVm2vIT2O3nsAKvfx1Mh9TIUFFCsDo
/PnrcK3X8HdGj8GLEXbU9kMwti0U9cuNwPiFEdLlGxhNZDETj4XslnAZkwP83FwC
DSoRhf2f6VAs6LqFGzYfedFR30ECAwEAATANBgkqhkiG9w0BAQsFAAOBgQAnuiB9
lxiV8ZIzElUx0JMxGXdhdxeKGouTpXysbVpqsppYe258bt9pYddU19ZedGgmOPT3
GVd60CoHCMWAJhMdVNpW+09bC+5hqNLGrAHM38bMEJkhHxAA5NUSwfC594K8j5bT
Plqei6QtutsTZ9FYLiuWhk5EufYgZJMsD9t/TA==
-----END CERTIFICATE-----

• 二进制文件，直接查看是乱码，所以使用Base64编码

案例3：

通过.crt证书，生成.der证书

openssl x509 -outform der -in rsacert.crt -out rsacert.der

• .der就是公钥

目录下生成rsacert.der证书文件

案例4：

通过私钥和.crt证书，导出.p12证书

openssl pkcs12 -export -out p.p12 -inkey private.pem -in rsacert.crt
-------------------------
Enter Export Password:
Verifying - Enter Export Password:

• 需要对.p12设置密码
• .p12就是私钥

目录下生成p.p12证书文件

.p12和.der证书是一对，分别对应私钥和公钥

案例5：

使用RSA代码加解密

打开RSADemo项目，将.p12和.der证书拖进项目中

• 勾选Add to targets选项

使用RSACryptor库，提供以下方法：

```

import

@interface RSACryptor : NSObject

• (instancetype)sharedRSACryptor;

//生成密钥对

• (void)generateKeyPair:(NSUInteger)keySize; //加载公钥
• (void)loadPublicKey:(NSString *)publicKeyPath; //加载私钥
• (void)loadPrivateKey:(NSString )privateKeyPath password:(NSString >)password; //加密数据
• (NSData )encryptData:(NSData )plainData; //解密数据
• (NSData )decryptData:(NSData )cipherData;

@end

> 打开`ViewController.m`文件，加载`公钥`和`私钥`
>

import “ViewController.h”

import “RSACryptor.h”

@implementation ViewController

• (void)viewDidLoad { [super viewDidLoad];

  [[RSACryptor sharedRSACryptor] loadPublicKey:[[NSBundle mainBundle] pathForResource:@”rsacert.der” ofType:nil]]; [[RSACryptor sharedRSACryptor] loadPrivateKey:[[NSBundle mainBundle] pathForResource:@”p.p12” ofType:nil] password:@”123456”]; }

@end

> 在`touchesBegan`方法中，实现`RSA`加解密代码
>

-(void)touchesBegan:(NSSet )touches withEvent:(UIEvent )event { NSString *strText = @”hello”;

NSData dataEncrypt = [[RSACryptor sharedRSACryptor] encryptData:[strText dataUsingEncoding:NSUTF8StringEncoding]]; NSString strEncrypt = [dataEncrypt base64EncodedStringWithOptions:0]; NSLog(@”加密：%@”, strEncrypt);

NSData dataDecrypt = [[RSACryptor sharedRSACryptor] decryptData:dataEncrypt]; NSString strDecrypt = [[NSString alloc] initWithData:dataDecrypt encoding:NSUTF8StringEncoding]; NSLog(@”解密：%@”, strDecrypt); }

> - 加密和解密，返回的都是二进制数据，无法直接查看
> 运行项目，点击屏幕，输出以下内容：
>

加密：Lw+Qvesbk1QfSyXh/dGoGmGuUngZQVUhnsLA+zFFaAqF8U2NJY/lAArzH2RZ2mdIGA5+ty2SHS+lWUshTsJebteC9JR7lydw31mIlWac4EtEue4ZaJZAYOALBVSGVKlW9q8Ra4hW9KRBFdDfzFa+0BFn0d6P7Xfv5M15IwOuDfc= 解密：hello

> - 将加密后二进制数据，进行`Base64`编码，可查看编码后内容
> - 将解密后二进制信息，进行`UTF8`编码，可查看原文内容
> 案例6：
> `RSA`加密的填充方式
> 上述案例，每次点击屏幕，输出的加密结果都不同，但都能解密成原文`hello`
>

加密：NL64/eVWYq7VRS/dqLDTw5WvH1kdLj/ODE5lbeA5C9pT7dDFz2f3hDVN3YjiY6/grMH2QgVvV6sX7mkb+YpmBXHakT13+vtyIw35YJcYb4w9gMzUwyWj6qynS1w3Mg8NioVzFO0diiP5Z/eIPNGS3TX2oeaY7imPSm2awuajO2k= 加密：ajIiKWwXi9OkykqE4nBW8G/hQ1LzyT0+aUqTdiSlQt40Svgj/10mn/gC1OM0Xom6HDX+5R8M9+rHFEK9eM4UrifYKDr+AKsP+rlNFmGEHTyZ5FZwUVVsM7rcNymbCSVvC3S6TPQY3i/G1IuLbiV7rffYufz4ew1b08fnR+tmRHU= 加密：AHth9iyax8banLC7yUJMWxLAZMRY2z/2v7flXoZu/TroPZybT+UzkrSV/haLJDOesqa514BgAnNq7s6vni9uA1yTO0UP2gaTWjvv7CB/TYCPVcALPdd+2FklBvMfXZCcWXpvXZBYQKtt8Fx59REiIKBoVz5tzNR5vz6+5Qj9DPY=

> 这种现象，和代码中`RSA`加密的填充方式有关
>

define kTypeOfWrapPadding kSecPaddingPKCS1

```

RSA加密的三种填充方式

• kSecPaddingNone：不填充，每次生成的加密结果都一样
• kSecPaddingPKCS1：最常用的填充方式，默认项
• kSecPaddingOAEP：PKCS#1推出的新的填充方式，安全性是最高

---

假如密钥长度为1024bit，即：128Byte：

• 当客户端选择kSecPaddingNone填充模式时，如果明文不够128字节，加密时会在明文前面，前向填充零，每次生成的加密结果都一样。服务端在解密后，用相同的方式把前向填充的零去掉，才能得到真正的明文
• 当选择kSecPaddingPKCS1填充模式时，如果明文不够128字节，会在明文中随机填充一些数据，所以会导致对同样的明文每次加密后的结果都不一样。对加密后的密文，服务端使用相同的填充方式解密
• kSecPaddingOAEP填充模式， 是PKCS#1推出的新的填充方式，安全性是最高的，和前面kSecPaddingPKCS1的区别就是加密前的编码方式不一样

总结

密码学概述

• 加密算法，都是数学知识
• 对称加密是传统加密算法
• RSA非对称加密是现代加密算法
• RSA是三位数学家的名字

RSA数学原理

• 质数
• 原根
• 欧拉函数
• 欧拉定理
• 费马小定理（正向计算容易，反算难）
• 模反元素：m ^ (e * d) % n = m，目的找出e和d
• 迪菲赫尔曼密钥交换

RSA算法

• RSA拆解两个大质数的乘积很难，所以相对安全
• 加密：m ^ e % n = c
• 解密：c ^ d % n = m
• 公钥：n和e
• 私钥：n和d
• 明文：m
• 密文：c

RSA成立条件

• m必须小于n
• n是由两个质数相乘，得到一个很大的数。目的是方便求出φ(n)
• d是e相对φ(n)的模反元素
• n可以公开，但无法计算组成n的两个质数p1和p2，找不出p1和p2就无法计算φ(n)，找不出φ(n)就无法计算e和d
• e在使用OpenSSL生成私钥时，设定为65537

RSA的特点

• 加密安全系数非常高
• 加密效率低
• 不适合加密大数据
• 仅用于加密关键数据
• 配合对称加密使用

RSA算法常用指令

• genrsa：生成并输入一个RSA私钥
• result：使用RSA密钥进行加密、解密、签名和验证等运算
• rsa：处理RSA密钥的格式转换等问题

代码演示

• 私钥和公钥使用p12和der格式

RSA加密的填充方式

• kSecPaddingNone：不填充，每次生成的加密结果都一样
• kSecPaddingPKCS1：最常用的填充方式，默认项
• kSecPaddingOAEP：PKCS#1推出的新的填充方式，安全性是最高