- 1、用筛选法求100之内的素数
- 2、用选择法对 10 个整数排序
- 3、求一个3×3的整型矩阵对角线元素之和
- 4、有一个已排好序的数组,要求输入一个数后,按原来排序的规律将它插入数组中。
- include
- define N 20
- 9、有 15 个数按由大到小顺序存放在一个数组中,输入一个数,要求用折半查找法找出该数是数组中第几个元素的值。如果该数不在数组中,则输出“无此数”。
- 5、将一个数组中的值按逆序重新存放。例如,原来顺序为
8,6,5,4,1要求改为1,4,5,6,8。 - include
- define N 10
- include
- 7、输出“魔方阵”。所谓魔方阵是指这样的方阵,它的每一行、每- -列和对角线之和均相等。例如,三阶魔方阵为
- 8、找出一个二维数组中的鞍点,即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点
- 10、有一篇文章,共有 3 行文字,每行有 80 个字符。要求分别统计出其中英文大写字母、小写字母、数字、空格以及其他字符的个数。
- 11、输出以下图案:
- 12、有一行电文,已按下面规律译成密码:
1、用筛选法求100之内的素数
2、用选择法对 10 个整数排序
3、求一个3×3的整型矩阵对角线元素之和
解题思路:矩阵对角线有一个性质就是行列的索引值是相等的。那么只需要判断 row = col 时就将其累加即可。这里完全都可以不需要二维数组进行操作。
#include <stdio.h>#define N 3int main () {printf("Please input %d numbers: ", N * N);int sum = 0, n;for (int row = 0; row < N; row++) {for (int col = 0; col < N; col++) {scanf("%d", &n);if (row == col) {sum += n;}}}printf("sum = %d\n", sum);return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/dignoal.c -o ./bin/dignoal
b12@PC:~/chapter6$ ./bin/dignoal
Please input 9 numbers: 1 2 3 4 5
6 7 8 9
sum = 15
:::
关于IO问题,其实最不用担心的就是 scanf("%d", &n); 格式,它会自动跳过所有不是数字的字符,一直要你输入完全。如上,可以将 9 个数字全部写在一堆,还可以一行一个数字。但是若携带其他普通字符如果没满足 scanf 函数就认为结束,它直接不管是否整个格式字符都进行赋值了,直接返回赋值成功个数。
4、有一个已排好序的数组,要求输入一个数后,按原来排序的规律将它插入数组中。
解题思路:典型的二分搜索问题,对于数组是连续内存分布,想要移动或删除一个数非常麻烦,需要将“大部分”进行搬家操作。
- 搜索插入位置:暴力法和二分搜索
- 移动元素腾出位置
- 在腾出的位置中放入插入元素。

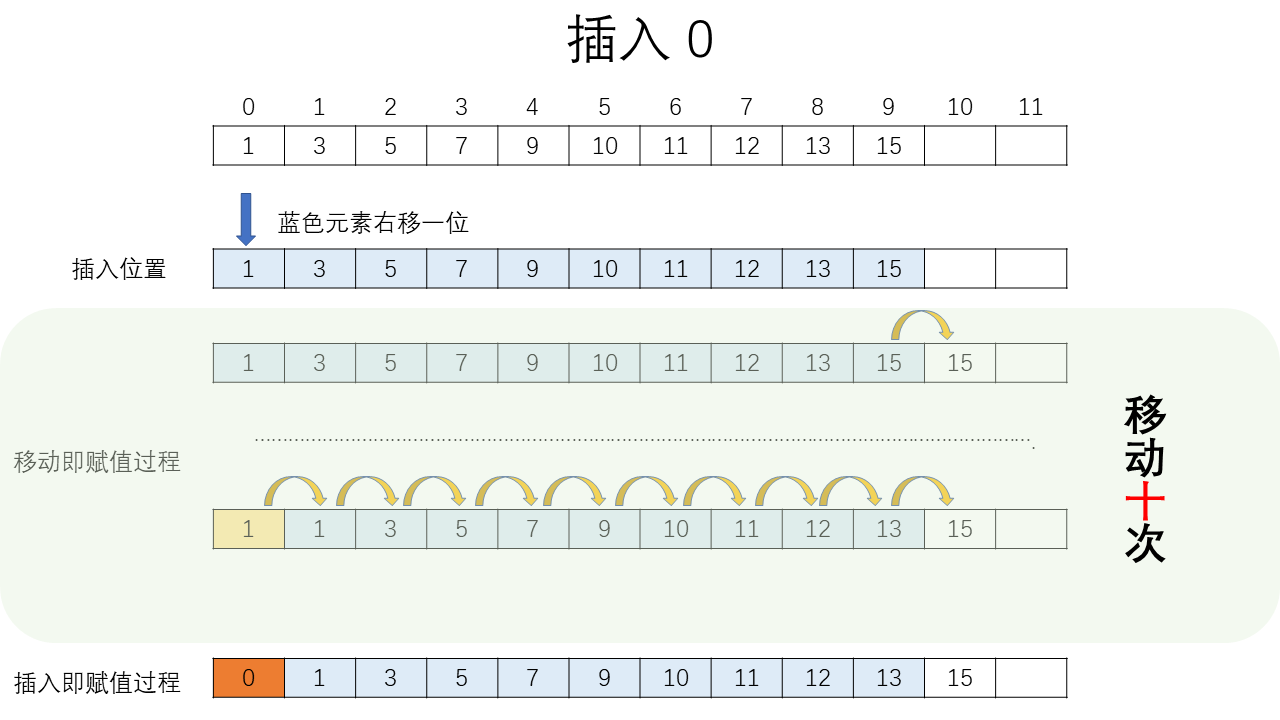
#include <stdio.h>#define N 20int main () {int nums[N] = {1, 3, 5, 7, 9, 11, 12, 13, 15}; // 其余初始化为0printf("Please input a number: ");int n, right = 9; // 假设初始有9个数字scanf("%d", &n);// 1.查找插入位置int idx = 0;while (idx < right && nums[idx] < n) { // 注意nums[i] <= n?idx++;}// 2.向后移动,后面的值赋值前面的,直到将nums[idx]赋值完成for (int i = right; i > idx; i--) {nums[i] = nums[i-1]; // 因为nums[i-1]刚好处于nums[idx]}// 3.向nums[idx]赋值插入元素nums[idx] = n;// 4.遍历输出数组,此时个数多一个for (int i = 0; i <= right; i++) {printf("%d ", nums[i]);}printf("\n");return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/bisectInsort.c -o ./bin/bisectInsort
b12@PC:~/chapter6$ ./bin/bisectInsort
Please input a number: 10
1 3 5 7 9 10 11 12 13 15
b12@PC:~/chapter6$ ./bin/bisectInsort
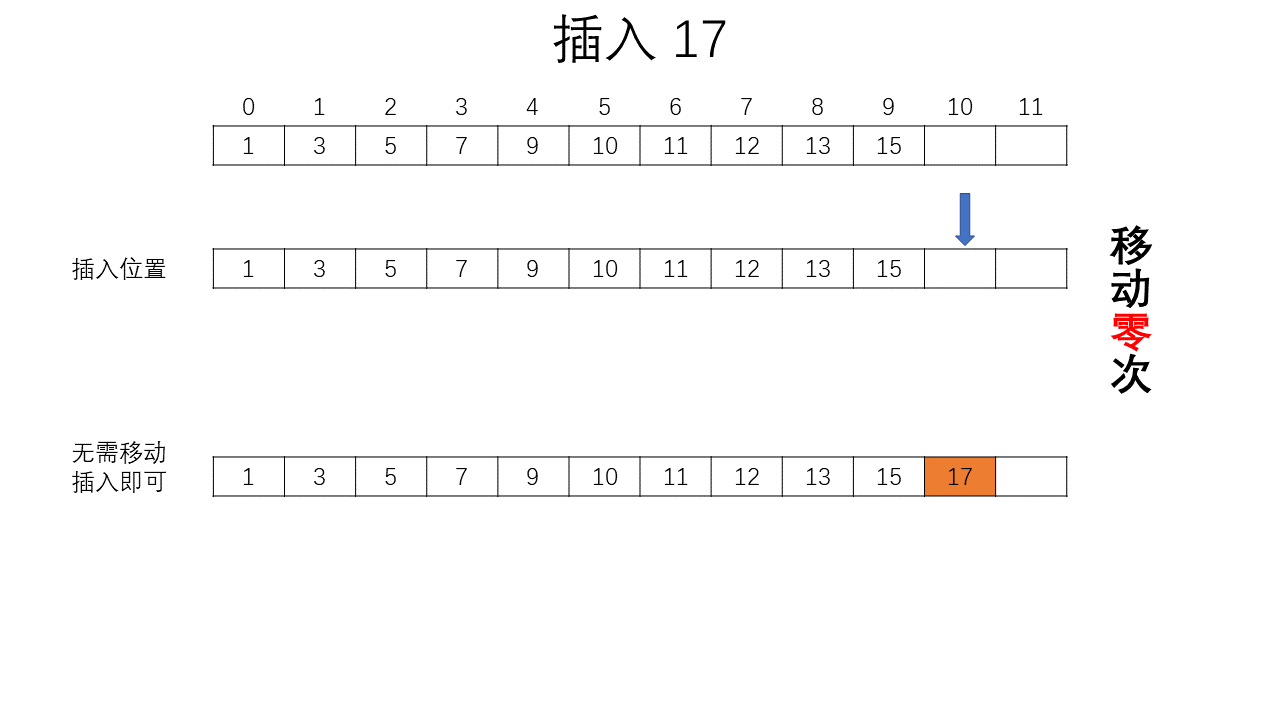
Please input a number: 17
1 3 5 7 9 11 12 13 15 17
b12@PC:~/chapter6$ ./bin/bisectInsort
Please input a number: 0
0 1 3 5 7 9 11 12 13 15
:::
问题:
- 为什么查找插入元素位置时等号是否可取呢?
答:等号完全在于个人是否可取,如果不可取,即 nums[i] = n 结束,证明此时就将原来和 n 一样的元素搬到右侧(当存在相等时,采用最左侧 leftmost 插入法)。如果取等号即循环条件为 ,那么当与原数组中存在相等时,采用
rightmost 插入法。因此取等号与否就在于若原数组存在相等的数,是否进行搬到。
但是这样暴力处理显然不好,没有完全用到数组有序的,因此二分搜索上场了。二分搜索本质就是收缩区间,将不可能的区间排除,最后答案直接出现。
强烈推荐我大哥题解:35. 搜索插入位置,弄懂二分可解决“绝大多数”有序数组问题。常见有序出现可能情况。
- 时间累加有序
- 成绩有序
- 数组索引天生有序
二分查找也是求解最值的一种方式。
int bisect_left(int *nums, int left, int right, int target) { while (left < right) { int mid = (right - left) / 2 + left; if (nums[mid] < target) { // 证明此时中间数小,右移左边界 left = mid + 1; } else { // 否则就可能是 >= 往左走 right = mid; } } return left; // 循环结束两者都是相等的 }
int main () { int nums[N] = {1, 3, 5, 7, 9, 11, 12, 13, 15}; // 其余初始化为0 printf(“Please input a number: “); int n, right = 9; // 假设初始有9个数字 scanf(“%d”, &n); // 1.查找插入位置 int idx = bisect_left(nums, 0, right, n); // 注意9索引表示在最后插入 // 2.向后移动,后面的值赋值前面的,直到将nums[idx]赋值完成 for (int i = right; i > idx; i—) { printf(“Move nums[%d] to nums[%d]\n”, i-1, i); nums[i] = nums[i-1]; // 因为nums[i-1]刚好处于nums[idx] } // 3.向nums[idx]赋值插入元素 nums[idx] = n; // 4.遍历输出数组,此时个数多一个 for (int i = 0; i <= right; i++) { printf(“%d “, nums[i]); } printf(“\n”); return 0; }
**编译运行**::::successb12@PC:~/chapter6$ gcc -Wall ./src/bisectInsort.c -o ./bin/bisectInsort<br />b12@PC:~/chapter6$ ./bin/bisectInsort<br />Please input a number: 9 # 搬动相同的<br />Move nums[8](15) to nums[9]<br />Move nums[7](13) to nums[8]<br />Move nums[6](12) to nums[7]<br />Move nums[5](11) to nums[6]<br />Move nums[4](9) to nums[5] # 9往右搬一次<br />1 3 5 7 9 9 11 12 13 15<br />b12@PC:~/chapter6$ ./bin/bisectInsort<br />Please input a number: 0<br />Move nums[8](15) to nums[9]<br />Move nums[7](13) to nums[8]<br />Move nums[6](12) to nums[7]<br />Move nums[5](11) to nums[6]<br />Move nums[4](9) to nums[5]<br />Move nums[3](7) to nums[4]<br />Move nums[2](5) to nums[3]<br />Move nums[1](3) to nums[2]<br />Move nums[0](1) to nums[1]<br />0 1 3 5 7 9 11 12 13 15<br />b12@PC:~/chapter6$ ./bin/bisectInsort<br />Please input a number: 17<br />1 3 5 7 9 11 12 13 15 17:::2. 求解 `rightmost` 插入位置。相等的时候也给不往后移动,具体将会以打印移动过程展示。```c#include <stdio.h>#define N 20int bisect_left(int *nums, int left, int right, int target) {while (left < right) {int mid = (right - left) / 2 + left;if (nums[mid] <= target) { // 证明此时小于等于,左指针右移动left = mid + 1;} else { // 否则就可能是 >= 往左走right = mid;}}return left; // 循环结束两者都是相等的}int main () {int nums[N] = {1, 3, 5, 7, 9, 11, 12, 13, 15}; // 其余初始化为0printf("Please input a number: ");int n, right = 9; // 假设初始有9个数字scanf("%d", &n);// 1.查找插入位置int idx = bisect_left(nums, 0, right, n); // 注意9索引表示在最后插入// 2.向后移动,后面的值赋值前面的,直到将nums[idx]赋值完成for (int i = right; i > idx; i--) {printf("Move nums[%d](%d) to nums[%d]\n", i-1, nums[i-1], i);nums[i] = nums[i-1]; // 因为nums[i-1]刚好处于nums[idx]}// 3.向nums[idx]赋值插入元素nums[idx] = n;// 4.遍历输出数组,此时个数多一个for (int i = 0; i <= right; i++) {printf("%d ", nums[i]);}printf("\n");return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/bisectInsort.c -o ./bin/bisectInsort
b12@PC:~/chapter6$ ./bin/bisectInsort
Please input a number: 9
Move nums8 to nums[9]
Move nums7 to nums[8]
Move nums6 to nums[7]
Move nums5 to nums[6] # 不再搬动9
1 3 5 7 9 9 11 12 13 15
b12@PC:~/chapter6$ ./bin/bisectInsort
Please input a number: 15
1 3 5 7 9 11 12 13 15 15
b12@PC:~/chapter6$ ./bin/bisectInsort
Please input a number: 0
Move nums8 to nums[9]
Move nums7 to nums[8]
Move nums6 to nums[7]
Move nums5 to nums[6]
Move nums4 to nums[5]
Move nums3 to nums[4]
Move nums2 to nums[3]
Move nums1 to nums[2]
Move nums0 to nums[1]
0 1 3 5 7 9 11 12 13 15
:::
综上,两种差异就是求解上下界的问题,最大区别就是若查找元素相等时,收缩区间的差异导致最终的结果不同。写二分法,只写你拿得准的区间,两一个区间一定是互斥的,因此直接 if-else 搞定。
9、有 15 个数按由大到小顺序存放在一个数组中,输入一个数,要求用折半查找法找出该数是数组中第几个元素的值。如果该数不在数组中,则输出“无此数”。
解题思路:此题与上面非常类似,就是二分查找,不同的是最后的判断问题。一般来讲 while(left < right) 和 while (left <= right) 两者没有本质区别,都是二分缩减区间的思想,但是处理是否存在(后者较好理解)和范围(前者更适用)问题就需要对最后循环结果进行判断(我没搞懂书本上搞那么复杂干嘛?)。
#include <stdio.h>#define N 15int bisect(int *nums, int left, int right, int target) {while (left <= right) { // 闭区间?int mid = (right - left) / 2 + left; // 防止溢出if (nums[mid] < target) { // mid小,下轮区间 (mid, right]left = mid + 1; // 为什么+1?可不用+1吗?} else if (nums[mid] == target) { // 找到nums[mid]=targetreturn mid;} else { // mi大,下轮区间 [left,mid)right = mid - 1; // 为什么-1?可不用-1吗?}}return -1; // 表示没找到}int main() {int arr[] = {1, 3, 4, 5, 6, 8, 12, 23, 34, 44, 45, 56, 57, 58, 68};// 1.打印给观众看升序数字for (int i = 0; i < N; i++) printf("%d ", arr[i]);printf("\n");// 2.循环输出,用户选择退出while (1) {int number, idx;printf("Please input a number to find:");scanf("%d", &number);idx = bisect(arr, 0, N - 1, number); // 二分查找if (-1 == idx) {printf("No found\n");} else {printf("Index: %d\n", idx + 1); // 书本+1}printf("Continue or not<Y/N>:");getchar(); // 注意为什么?因为吸收空格char choice = getchar();if ('N' == choice || 'n' == choice) break;}return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/bisect.c -o ./bin/bisect
b12@PC:~/chapter6$ ./bin/bisect
1 3 4 5 6 8 12 23 34 44 45 56 57 58 68
Please input a number to find:7
No found
Continue or not
Please input a number to find:12
Index: 7
Continue or not
char choice;scanf(" %c", &choice); // 注意为什么?因为吸收换行符
为什么要在前面添加空格呢?因为空格在 scanf 作用很强大,可以跳过空白符。也是吸收由上面输入查找数字之后的 \n 。如果不加就会出现 choice = '\n' 的情况,循环永远不会停止。
:::warning
b12@PC:~/chapter6$ gcc -Wall ./src/bisect.c -o ./bin/bisect
b12@PC:~/chapter6$ ./bin/bisect
1 3 4 5 6 8 12 23 34 44 45 56 57 58 68
Please input a number to find:7
No found
Continue or not
Index: 7
Continue or not
5、将一个数组中的值按逆序重新存放。例如,原来顺序为8,6,5,4,1 要求改为1,4,5,6,8。
解题思路:本题有两种想法可以实现,都是根据关于中心点对称方式实现。例如长度为 N 的数组,最左侧假设是 left ,那么最右侧与之相对的肯定是 right + left = N 成立。
- 方法一:只枚举
left所在位置可能性,根据公式则有right = N - left。- 为什么下面是
N-i-1,因为数组下标从0开始! - 为什么循环条件是
,就是因为在
C语言中出现向下取整的整数除法,因而对于长度为奇偶都进行到中心。例如长度为偶数数组arr[4] = {1, 2, 3, 4},中心点,显然是数组种第
3个元素结束,这与实际相符合。例如长度为奇数数组arr[3] = {1, 2, 3},中心点,显然是数组种第
2个元素结束,这与实际相符合。
- 为什么下面是
![4S)7EH~8V_]X3EBI~A3)93J.png](/uploads/projects/u1190503@kxnd8g/d887d45e80d8caf1c9cdc6b588000592.png)
- 方法二:不需要考虑上述除法个数,只要使用“双指针”(准确来说是索引下标),只要左边和右边的索引下标不重合,那么就交换。即相向运动过程种交换值即可,在相遇之时停止(为什么相遇停止?一个元素和自身交换有什么意义?如果不相遇停止,它们将会开始反向运动,又会交换回去了)。

void print(int arr[]) { // 这里规定数组长度N for (int i = 0; i < N; i++) { printf(“%d “, arr[i]); } printf(“\n”); }
int main() { int arr[N]; printf(“Please input %d numbers: “, N); for (int i = 0; i < N; i++) { scanf(“%d”, arr + i); // &arr[i] } printf(“Reverse1:\n”); for (int i = 0; i < N / 2; i++) { int tmp = arr[i]; arr[i] = arr[N-1-i]; arr[N-1-i] = tmp; } print(arr); printf(“Reverse2:\n”); for (int left = 0, right = N - 1; left < right; left++, right—) { int tmp = arr[left]; arr[left] = arr[right]; arr[right] = tmp; } print(arr); return 0; }
// 2.递归处理
include
void reverse(int n) { int x; scanf(“%d”, &x); if (1 == n) { // 递归终止,开始退栈 printf(“%d”, x); return; } reverse(n - 1); printf(“%d “, x); // 开始打印第二个 }
int main () { int n; scanf(“%d”, &n); reverse(n); return 0; }
**编译运行**::::successb12@PC:~/chapter6$ gcc -Wall ./src/reverse.c -o ./bin/reverse<br />b12@PC:~/chapter6$ ./bin/reverse<br />Please input 10 numbers: 0 1 2 3 4 5 6 7 8 9<br />Reverse1:<br />9 8 7 6 5 4 3 2 1 0<br />Reverse2:<br />0 1 2 3 4 5 6 7 8 9:::<a name="m0jgO"></a># 6、输出以下的杨辉三角形(要求输出10行)[118. 杨辉三角(简单)](https://www.yuque.com/u1190503/lsb24f/bqg8i7?view=doc_embed)<br />将上面的代码抠出来,放进 `main` 函数调用即可,但是注意此处函数传指针操作(**不懂跳过,待讲解指针和函数设计目的即可明白**)这里函数在的数组完全可以替换为**静态数组**。```c#include <stdio.h>#include <stdlib.h>int** generate(int numRows, int* returnSize, int** returnColumnSizes){*returnSize = numRows;*returnColumnSizes = (int *)malloc(sizeof(int)*numRows);int** res = (int**)malloc(sizeof(int*)*numRows);for (int i = 0; i < numRows; i++) {(*returnColumnSizes)[i] = i+1;res[i] = (int*)malloc(sizeof(int)*(i+1));res[i][0] = 1;res[i][i] = 1;for (int j = 1; j < i; j++) {res[i][j] = res[i-1][j] + res[i-1][j-1];}}return res;}int main() {printf("Please input row:");int numRows, size; // size 就是调用函数告诉返回数组指针内含有多少行scanf("%d", &numRows);int *ColumnSizes; // ColumnSizes是指针,传入函数修改赋值int **res = generate(numRows, &size, &ColumnSizes);for (int i = 0; i < size; i++) {for (int j = 0; j < ColumnSizes[i]; j++) {printf("%d ", res[i][j]);}printf("\n");}return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/pascalTriangle.c -o ./bin/pascalTriangle
b12@PC:~/chapter6$ ./bin/pascalTriangle
Please input row:10
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
:::
如果想要那种格式对齐,金字塔型,需要计算出每行左侧空格数,但是由于后面数字是两位数,任然会出现“错位”,因此实现无意义。
7、输出“魔方阵”。所谓魔方阵是指这样的方阵,它的每一行、每- -列和对角线之和均相等。例如,三阶魔方阵为
| 8 | 1 | 6 |
|---|---|---|
| 3 | 5 | 7 |
| 4 | 9 | 8 |
要求输出 的自然数构成的魔方阵。
解法一:暴力回溯(只适用于n = 3的枚举),对于每个位置matrix[i][j]其都有n*n种可能,但是本例是非重复使用,因此第一个位置有n*n种可能,第二个就只有n*n-1种,以此类推。不难发现这个算法复杂度为 ,所以当n > 3后直接爆炸,算很久都算不出来!
#include <stdio.h>#define N 3int backtrace(int matrix[N][N], int r, int c, int used[N]) {if (r == N) { // 终点int k = -1;for (int i = 0; i < N; ++i) { // (1) 检测每行和是否相同int sum = 0;for (int j = 0; j < N; ++j) sum += matrix[i][j];if (-1 == k) k = sum; // 第一行之和else if (k != sum) return 0;}for (int j = 0; j < N; ++j) { // (2) 检测每列和是否相同int sum = 0;for (int i = 0; i < N; ++i) sum += matrix[i][j];if (k != sum) return 0;}int sum = 0;for (int i = 0; i < N; ++i) { // (3) 检测主对角线sum += matrix[i][i];}for (int j = N - 1, i = 0; j >= 0; --j, ++i) { // (4) 检测副对角线sum -= matrix[i][j];}return 0 == sum;}if (c == N) return backtrace(matrix, r + 1, 0, used); // 换行继续// 当前 matrix[r][c] 填充数字for (int x = 0; x < N * N; ++x) {if (!used[x]) {used[x] = 1; // 选择matrix[r][c] = x + 1;if (backtrace(matrix, r, c + 1, used)) return 1;used[x] = 0; // 撤销}}return 0;}int main() {int matrix[N][N] = {0}, used[N * N] = {0};backtrace(matrix, 0, 0, used);// 打印结果for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) printf("%d ", matrix[i][j]);printf("\n");}return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/magicMatrix.c -o ./bin/magicMatrix
b12@PC:~/chapter6$ ./bin/magicMatrix
2 7 6
9 5 1
4 3 8
:::
解法二:我也不会,这种题目纯找规律,证明又很难,大家可看书或下面文章。
8、找出一个二维数组中的鞍点,即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点
10、有一篇文章,共有 3 行文字,每行有 80 个字符。要求分别统计出其中英文大写字母、小写字母、数字、空格以及其他字符的个数。
需要考虑多行 IO 问题,不用数组解决,而用 getchar() 方便。
PTA编程—循环1
11、输出以下图案:
*************************
解题思路:书本上示例含有空格,但是实际它代码中没有计算空格。如若考试有空格,只需要在下面代码中添加一个空格即 printf("%c ", fillchar);
#include <stdio.h>#define N 5int main() {char fillchar;int row;printf("Please input row & fillchar:");scanf("%d %c", &row, &fillchar);// 1.输出 row 行for (int i = 0; i < row; i++) {// 2.打印 i 的前缀空格for (int j = 0; j < i; j++) {printf(" ");}// 3.打印 fillcharfor (int j = 0; j < N; j++) {printf("%c", fillchar); // 此处可添加空格间隔}printf("\n"); // 换行}return 0;}
编译运行:
:::success
b12@PC:~/chapter6$ gcc -Wall ./src/printChar.c -o ./bin/printChar
b12@PC:~/chapter6$ ./bin/printChar
Please input row & fillchar:6 @
@@@@@
@@@@@
@@@@@
@@@@@
@@@@@
@@@@@
:::
12、有一行电文,已按下面规律译成密码:
| 大写 | 小写 | ||
|---|---|---|---|
| A | Z | a | z |
| B | Y | b | y |
| C | X | c | x |
| ……… | ……… | ||
| Z | A | z | a |
即第1个字母变成第26个字母,第i个字母变成第(26-i+1)个字母,非字母字符不变。要求编程序将密码译回原文,并输出密码和原文。
解题思路:本题就是首尾对于字母转换,设字符从 0->25 即 a->z ,必定存在 ,因此解方程即可。
- 大小写判断:可以分别判断大小写
- 先转换字母变为
0->25,即全部小写字母减去'a'的值再加上'a'输出转换后的字符,大写字母减去'A'的值再加上'A'输出转换后的字符。即公式:
编译运行: :::success $ gcc -Wall ./src/translate.c -o ./bin/translate#include <stdio.h>#define N 100int main() {char cipher[N], trans[N] = {0};printf("Please input cipher code:");scanf("%[^\n]s", cipher); // 非\n符号for (int i = 0; cipher[i] != '\0'; i++) {if ('A' <= cipher[i] && cipher[i] <= 'Z') { // (y-'A')=25-(x-'A')trans[i] = 25 - (cipher[i] - 'A') + 'A';} else if ('a' <= cipher[i] && cipher[i] <= 'z') {trans[i] = 25 - (cipher[i] - 'a') + 'a';} else {trans[i] = cipher[i];}}printf("cipher code:%s\n", cipher);printf("trans code:%s\n", trans);return 0;}
$ ./bin/translate
Please input cipher code:145da AFAew3451fga a
cipher code:145da AFAew3451fga a
trans code:145wz ZUZvd3451utz z :::

