- 练习10-1 使用递归函数计算1到n之和">练习10-1 使用递归函数计算1到n之和
- 习题10-2 递归求阶乘和">习题10-2 递归求阶乘和
- 习题10-3 递归实现指数函数">习题10-3 递归实现指数函数
- 习题10-4 递归求简单交错幂级数的部分和">习题10-4 递归求简单交错幂级数的部分和
- 习题10-5 递归计算Ackermenn函数">习题10-5 递归计算Ackermenn函数
- 习题10-6 递归求Fabonacci数列">习题10-6 递归求Fabonacci数列
- 习题10-7 十进制转换二进制">习题10-7 十进制转换二进制
- 习题10-8 递归实现顺序输出整数">习题10-8 递归实现顺序输出整数
练习10-1 使用递归函数计算1到n之和
本题要求实现一个用递归计算1+2+3+…+n的和的简单函数。
函数接口定义:
int sum( int n );
该函数对于传入的正整数n返回1+2+3+…+n的和;若n不是正整数则返回0。题目保证输入输出在长整型范围内。建议尝试写成递归函数。
裁判测试程序样例:
#include <stdio.h>int sum( int n );int main(){int n;scanf("%d", &n);printf ("%d\n", sum(n));return 0;}/* 你的代码将被嵌在这里 */
输入样例1:
10
输出样例1:
55
输入样例2:
0
输出样例2:
0
解题思路:本题虽然可以使用迭代或者高斯公式完成,但是为练习递归需要分析递归链+结束条件。
- 结束条件:当
n = 1时,可以直接返回1 - 递归链条:触发条件为
n != 1则继续求解sum(n - 1)
在 https://recursion.vercel.app/ 网站提交 python 代码,然后点击 RUN,就可以看到 sum(10) 递归函数执行过程。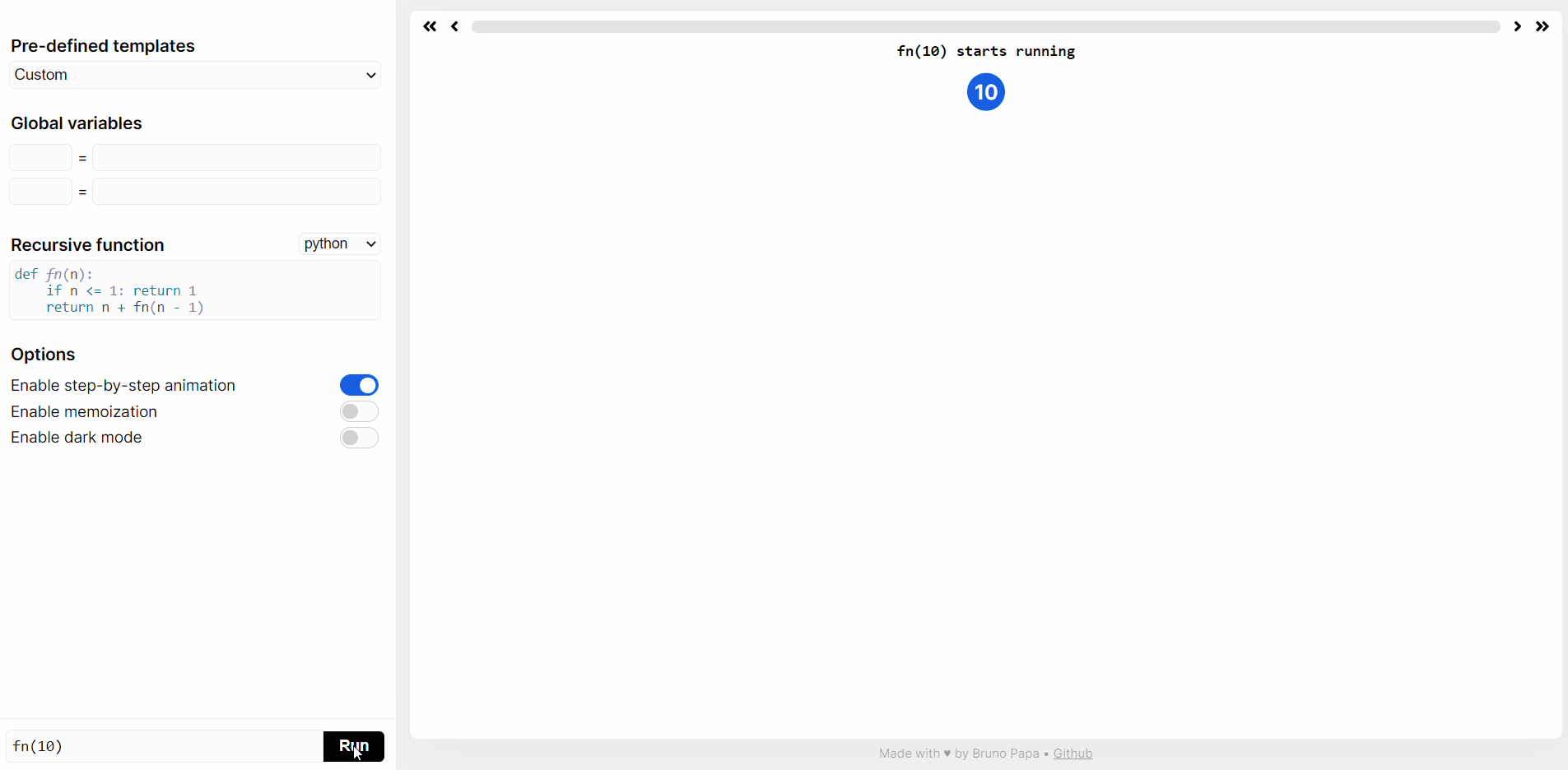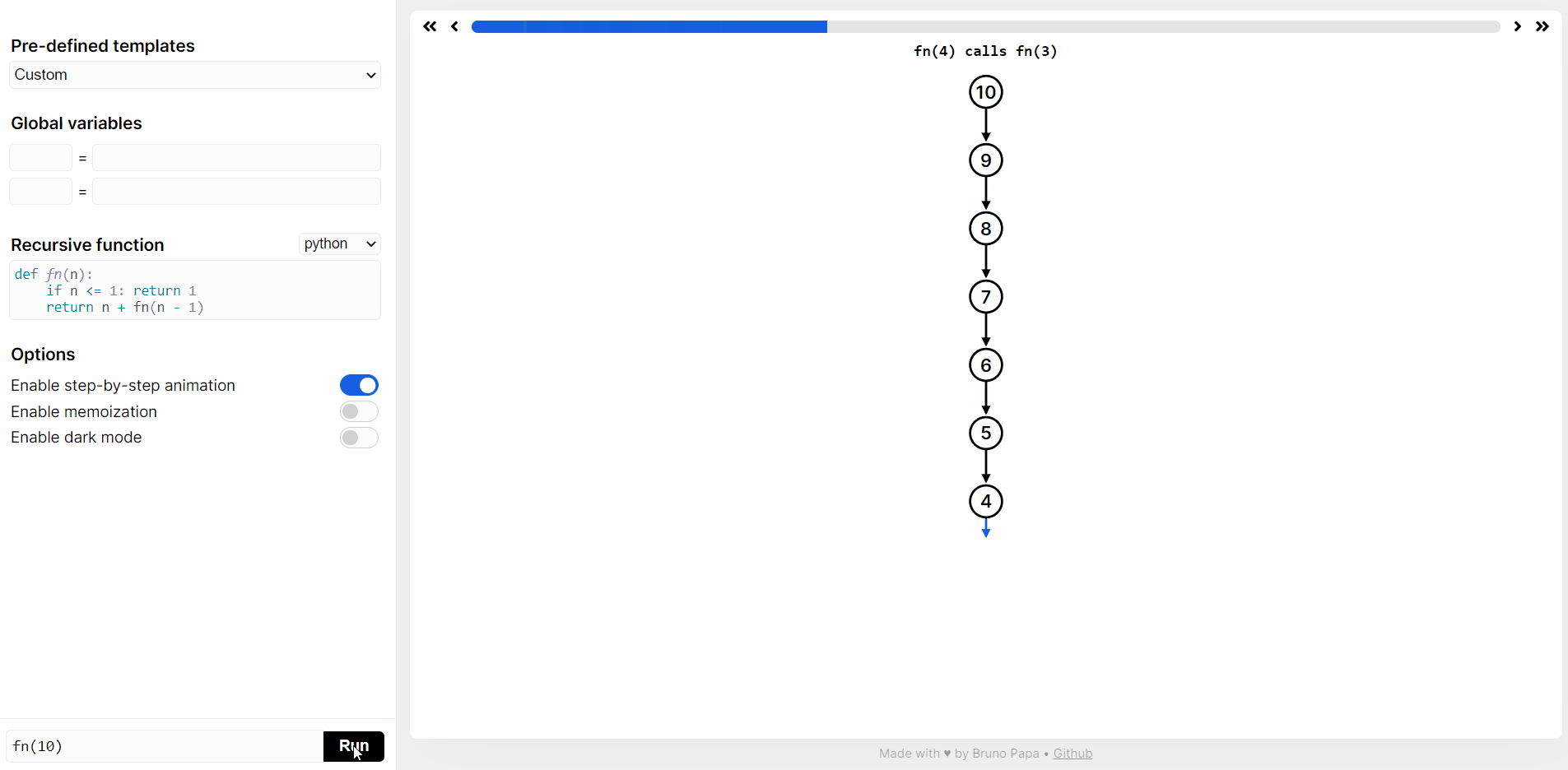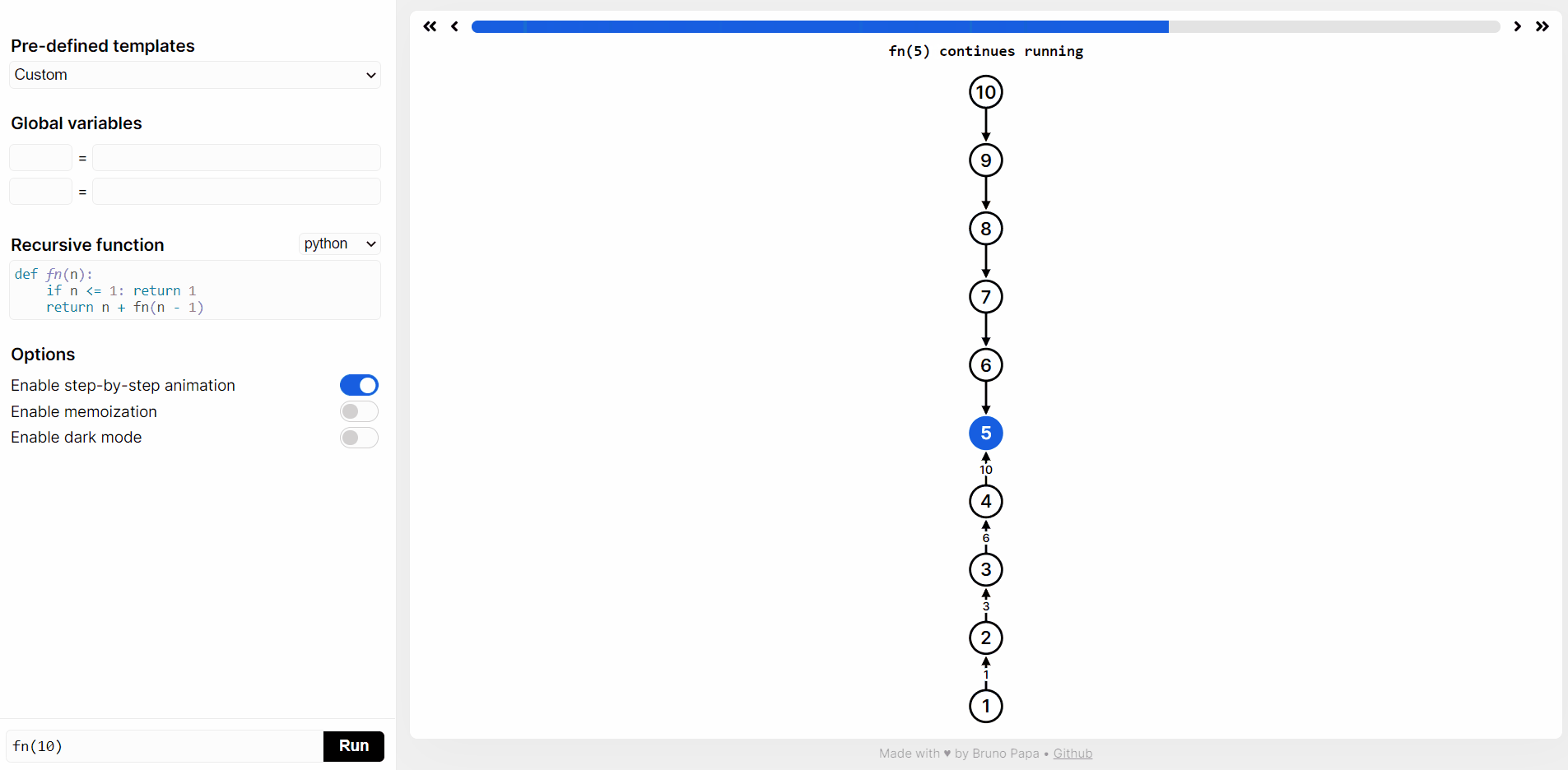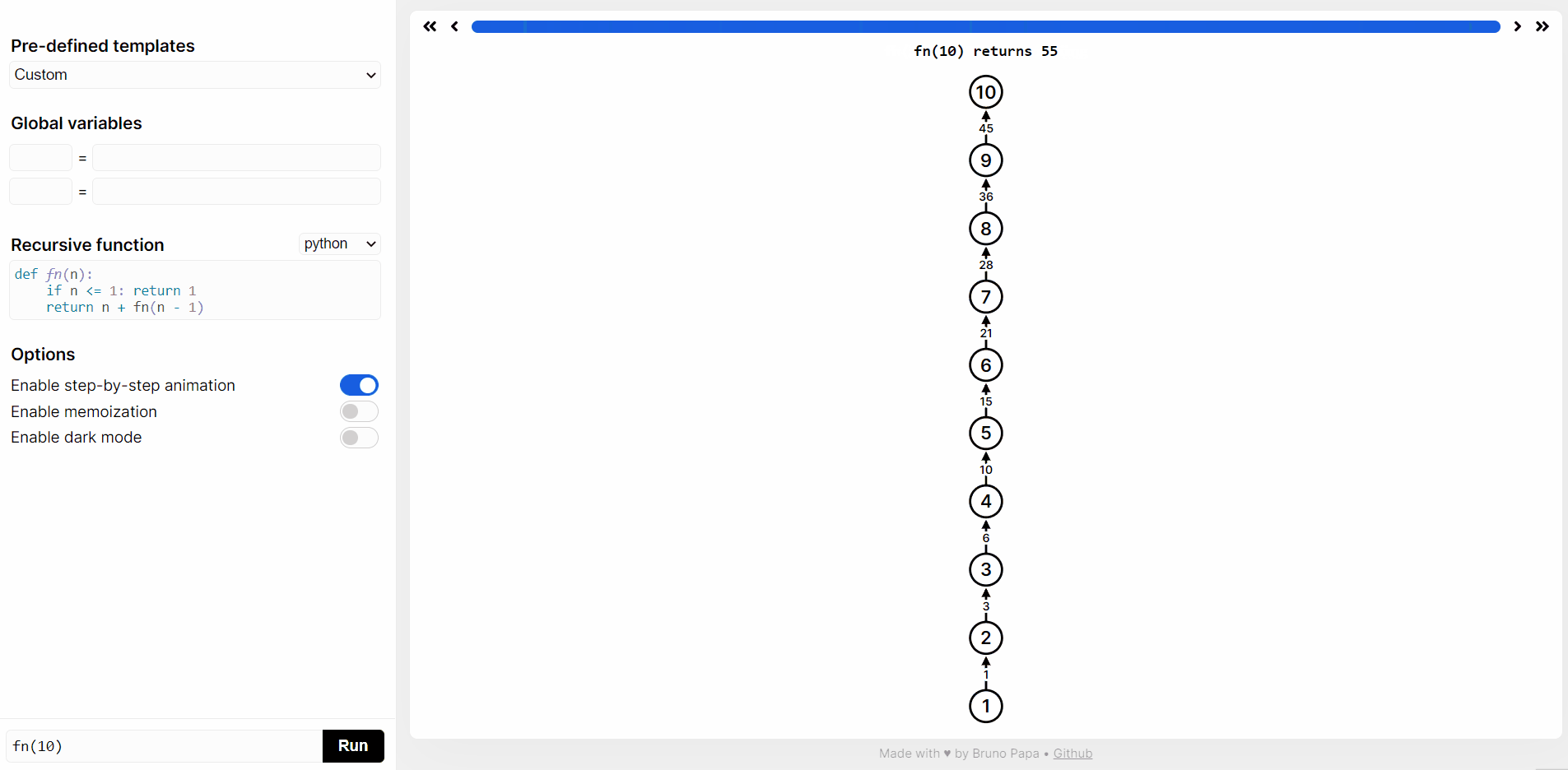
int sum(int n) {if (n <= 1) {return 1;}return n + sum(n - 1);}
复杂度分析:
- 时间复杂度:
- 空间复杂度:
,递归栈大小。 | Case | Hint | Result | Score | Run Time | Memory | | —- | —- | —- | —- | —- | —- | | 0 | sample等价 | Accepted | 7 | 4 ms | 232 KB | | 1 | n = 1 | Accepted | 1 | 4 ms | 384 KB | | 2 | n = 0 | Accepted | 1 | 4 ms | 256 KB | | 3 | n为负数 | Accepted | 1 | 3 ms | 384 KB |
习题10-2 递归求阶乘和
本题要求实现一个计算非负整数阶乘的简单函数,并利用该函数求 1!+2!+3!+…+n! 的值。
函数接口定义:
double fact( int n );double factsum( int n );
函数 fact 应返回 n 的阶乘,建议用递归实现。函数 factsum 应返回 1!+2!+…+n! 的值。题目保证输入输出在双精度范围内。
裁判测试程序样例:
#include <stdio.h>double fact( int n );double factsum( int n );int main(){int n;scanf("%d",&n);printf("fact(%d) = %.0f\n", n, fact(n));printf("sum = %.0f\n", factsum(n));return 0;}/* 你的代码将被嵌在这里 */
输入样例1:
10
输出样例1:
fact(10) = 3628800sum = 4037913
输入样例2:
0
输出样例2:
fact(0) = 1sum = 0
解题思路:本题虽然可以使用迭代完成,但是为练习递归求解阶乘需要分析递归链+结束条件。
- 结束条件:当
n = 0时,可以直接返回1,因为0! = 1。 - 递归链条:否则当
n > 0时,根据阶乘定义,将
n = n - 1带入原式得,可知递推式
(虽然这个可以用循环实现,但是本例要求用函数)
在 https://recursion.vercel.app/ 网站提交 python 代码,然后点击 RUN,就可以看到
fact(10)递归函数执行过程。
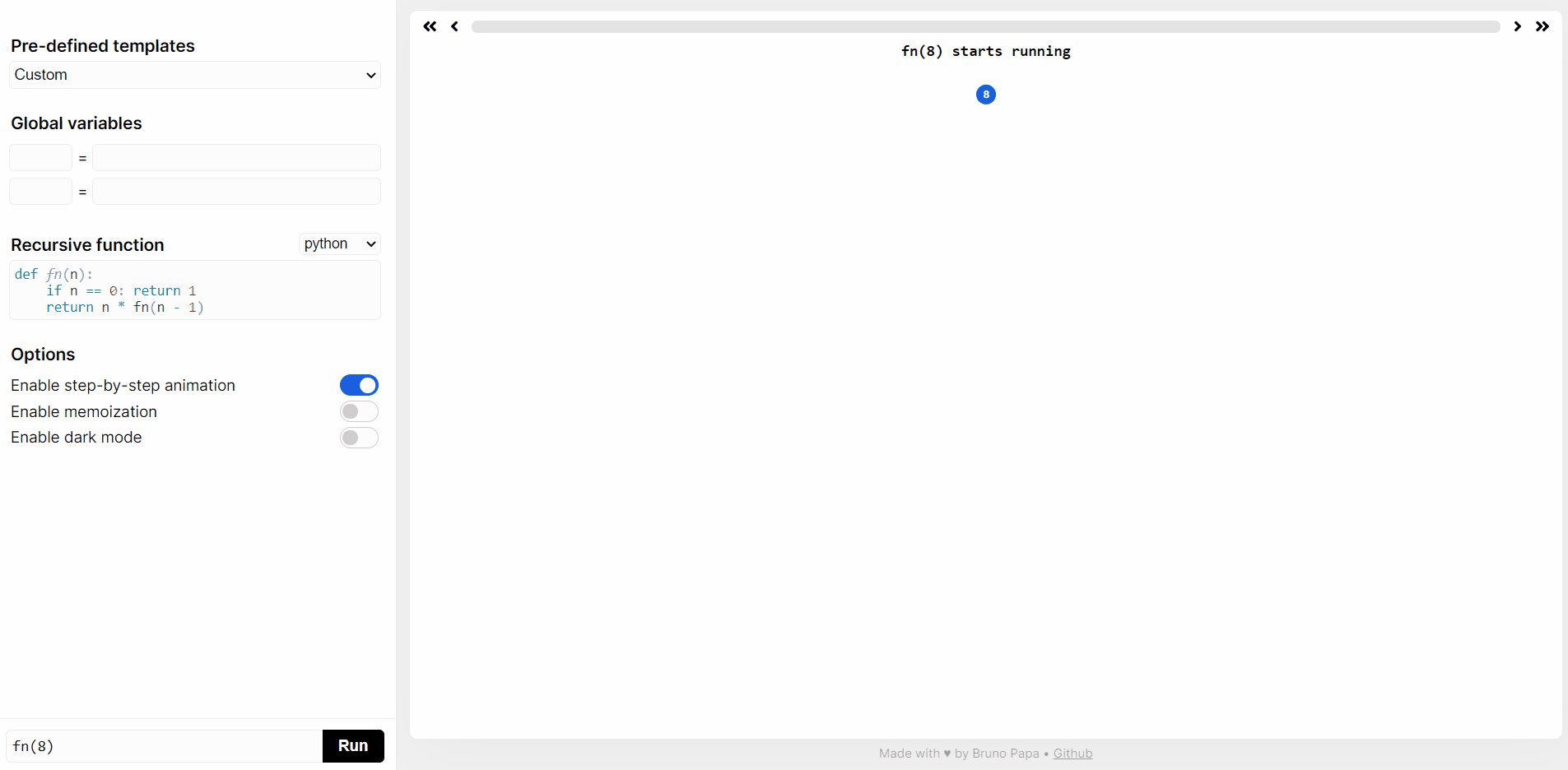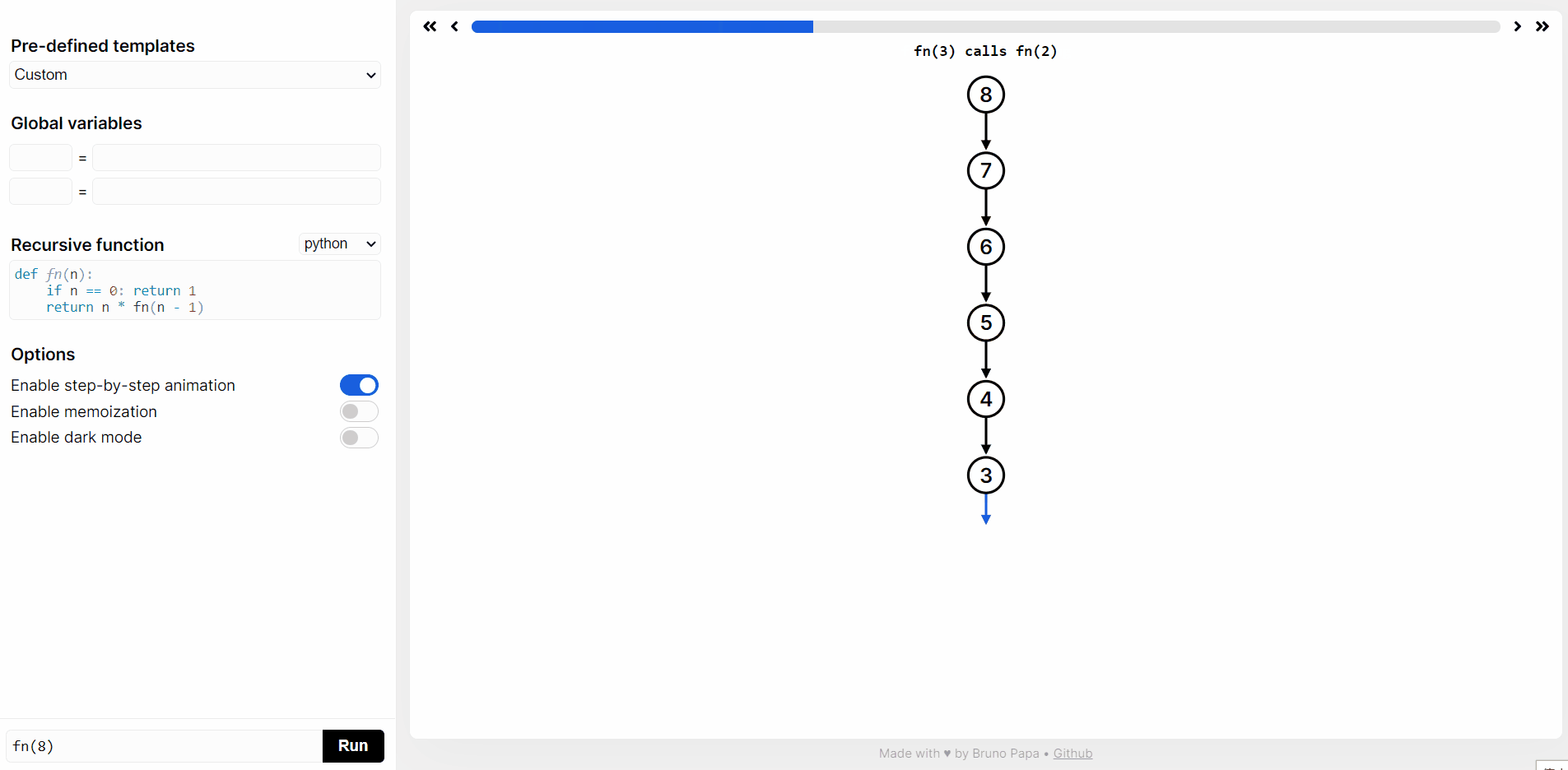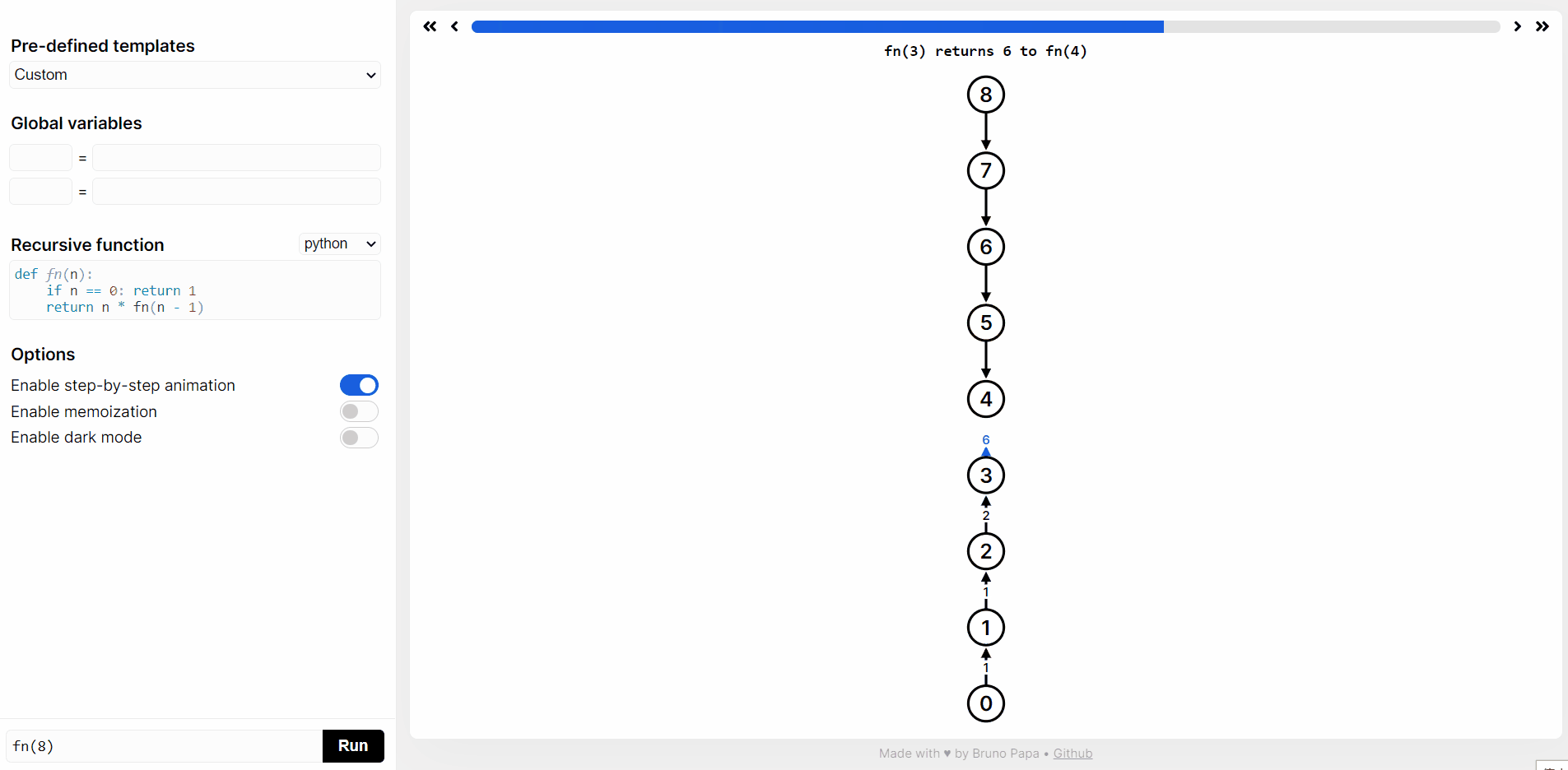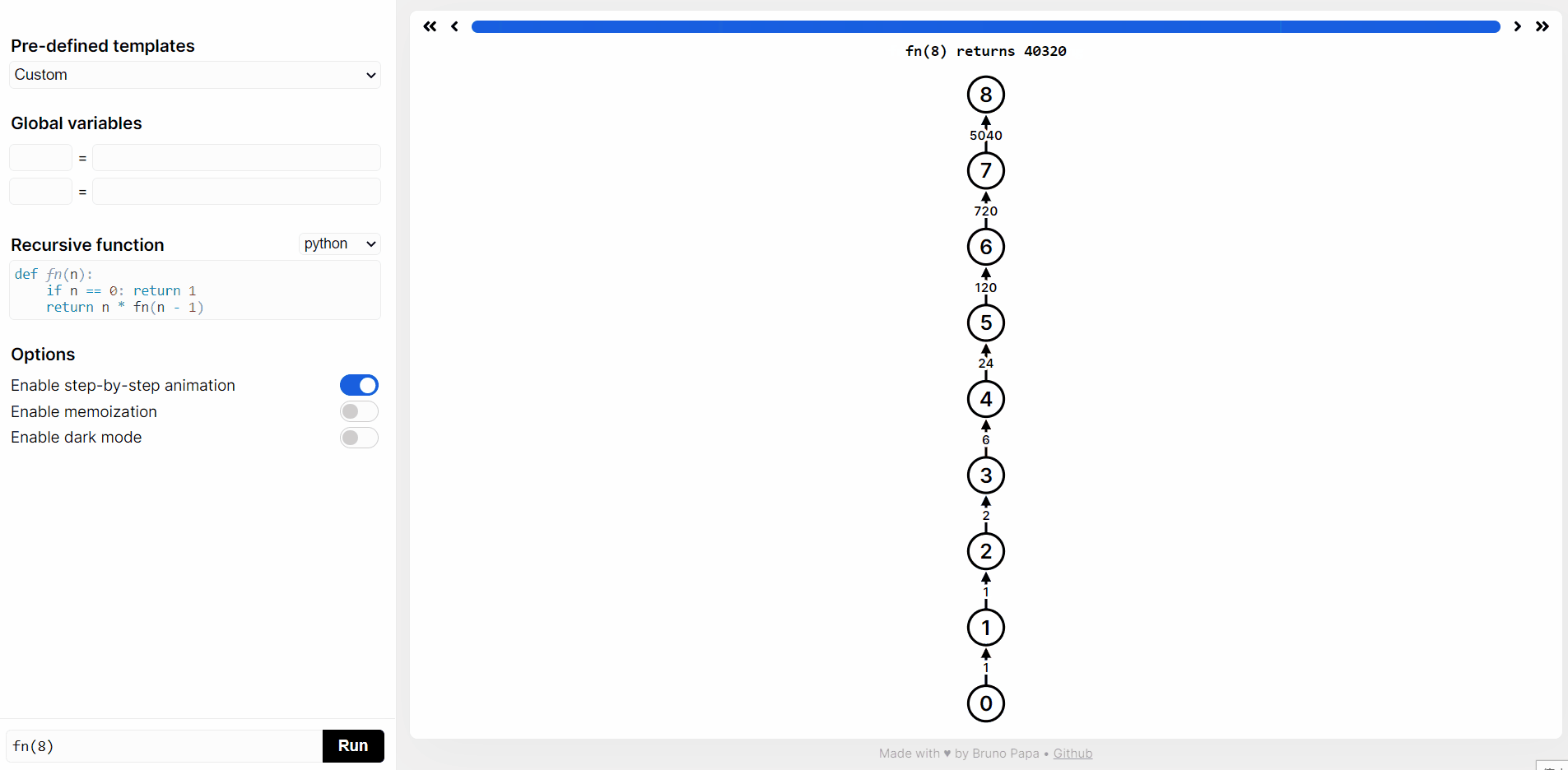
double fact(int n) {if (n <= 1) {return 1;}return n * fact(n - 1);}double factsum(int n) {double sum = 0;for (int i = 1; i <= n; i++) {sum += fact(i);}return sum;}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample 1等价 | Accepted | 11 | 2 ms | 256 KB |
| 1 | sample 2, n为0 | Accepted | 2 | 3 ms | 256 KB |
| 2 | n = 1 | Accepted | 2 | 3 ms | 256 KB |
本例可以优化地方在于 ,因此在求解
后,想要求解
直接×
n ,不必再从 1 开始累乘到 n 。
double fact(int n) {if (n <= 1) {return 1;}return n * fact(n - 1);}double factsum(int n) {double sum = 0, lastFact = 1.0;for (int i = 1; i <= n; ++i) {sum += lastFact * i;lastFact *= i;}return sum;}
习题10-3 递归实现指数函数
本题要求实现一个计算(n≥1)的函数。
函数接口定义:
double calc_pow( double x, int n );
函数calc_pow应返回x的n次幂的值。建议用递归实现。题目保证结果在双精度范围内。
裁判测试程序样例:
#include <stdio.h>double calc_pow( double x, int n );int main(){double x;int n;scanf("%lf %d", &x, &n);printf("%.0f\n", calc_pow(x, n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
2 3
输出样例:
8
解题思路:本题是经典的快速幂算法。对于考试只需要掌握暴力线性算法 即可,有兴趣的同学可以探究快速幂算法(递归版本较好理解;二进制迭代涉及位权和权值,它们时间复杂度为
)
语雀内容
本题暴力参考代码:
double calc_pow(double x, int n) {if (n == 0) {return 1;}return x * calc_pow(x, n - 1);}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价, n是奇数 | Accepted | 8 | 4 ms | 296 KB |
| 1 | n是偶数 | Accepted | 5 | 4 ms | 256 KB |
| 2 | n是1 | Accepted | 2 | 4 ms | 256 KB |
习题10-4 递归求简单交错幂级数的部分和
本题要求实现一个函数,计算下列简单交错幂级数的部分和:
函数接口定义:
double fn( double x, int n );
其中题目保证传入的n是正整数,并且输入输出都在双精度范围内。函数fn应返回上述级数的部分和。建议尝试用递归实现。
裁判测试程序样例:
#include <stdio.h>double fn( double x, int n );int main(){double x;int n;scanf("%lf %d", &x, &n);printf("%.2f\n", fn(x,n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
0.5 12
输出样例:
0.33
解题思路:题目最后一项给出通项公式 ,因此直接模拟即可。
- 递归终点:边界条件就是
n = 1时直接返回x - 递归边界:
,将
n = n-1带入通式得,两式相减得
综上,每次递归求解 (可以参考上题快速幂),然后剩余的逻辑交给递归函数求解
即可。
在 https://recursion.vercel.app/ 网站提交 python 代码,然后点击 RUN,就可以看到
f(0.5, 12)递归函数执行过程。
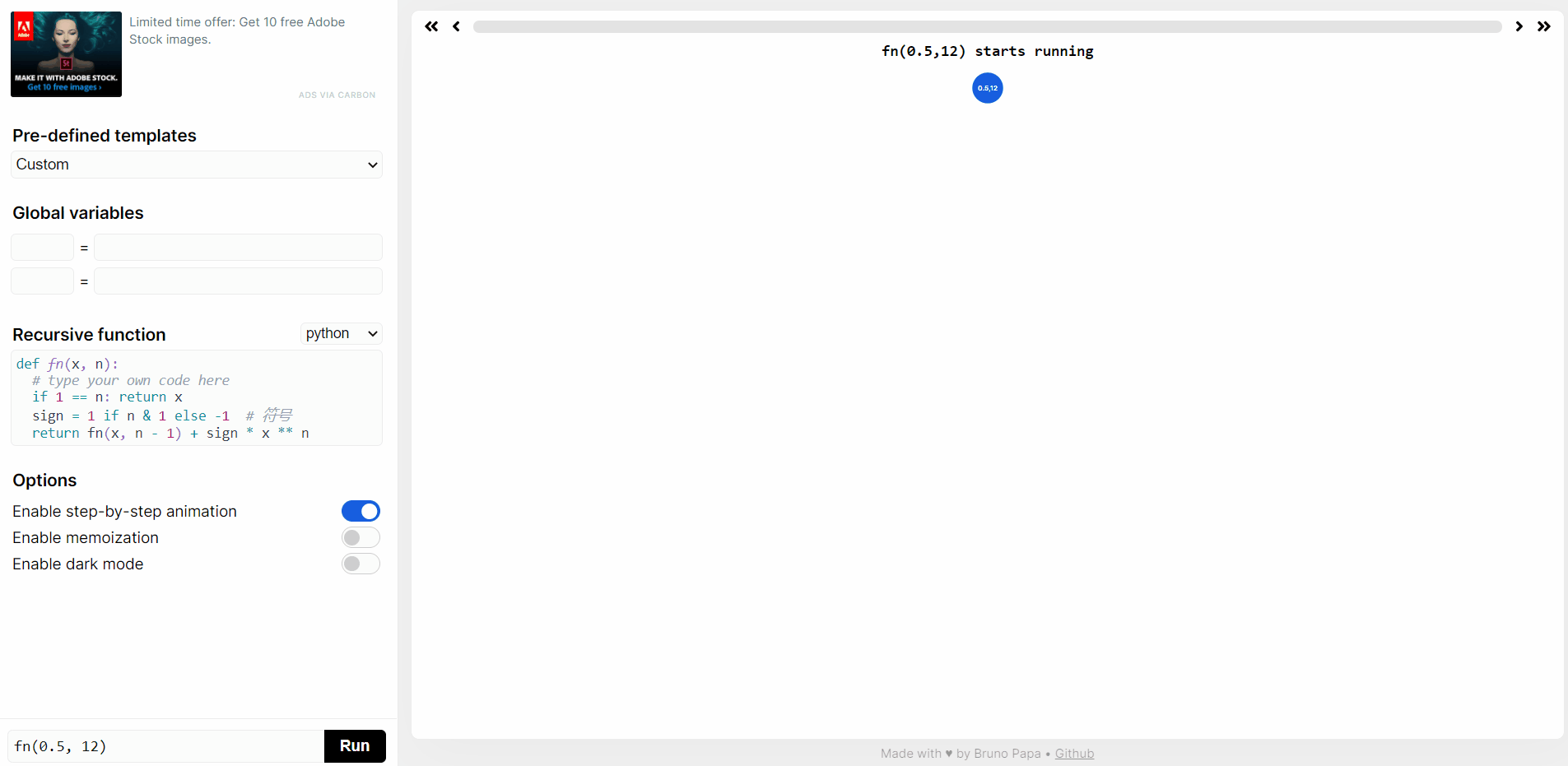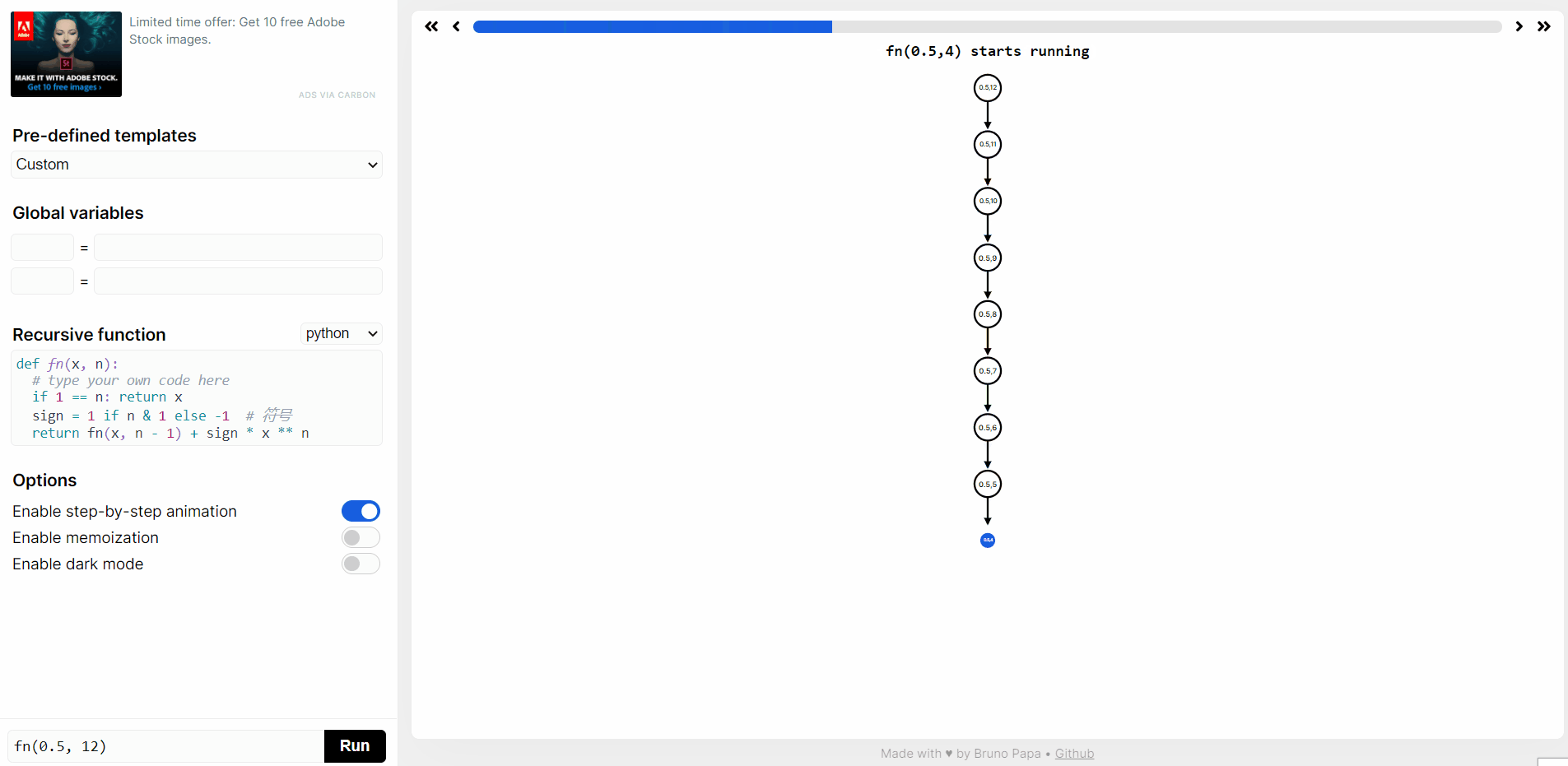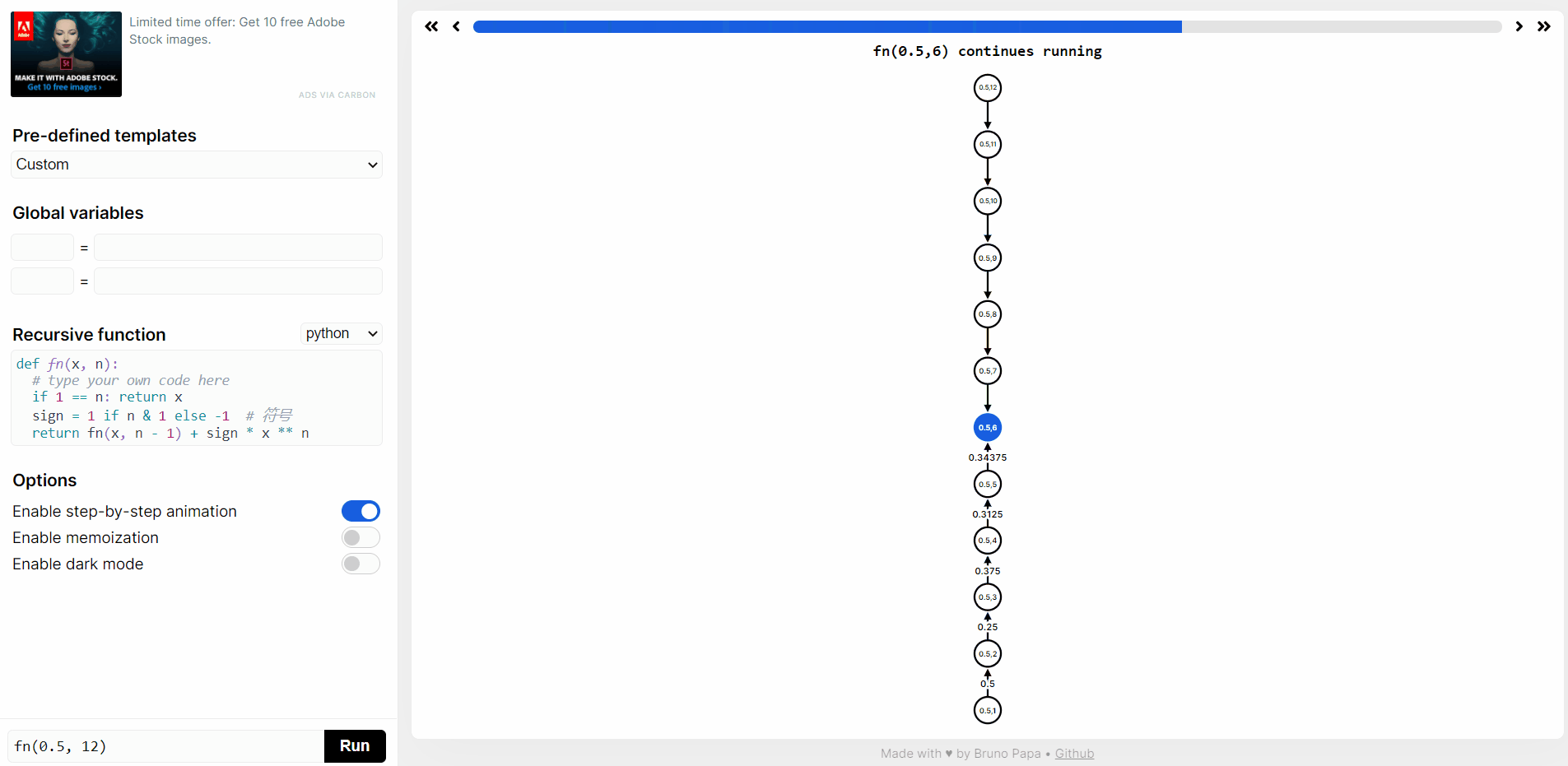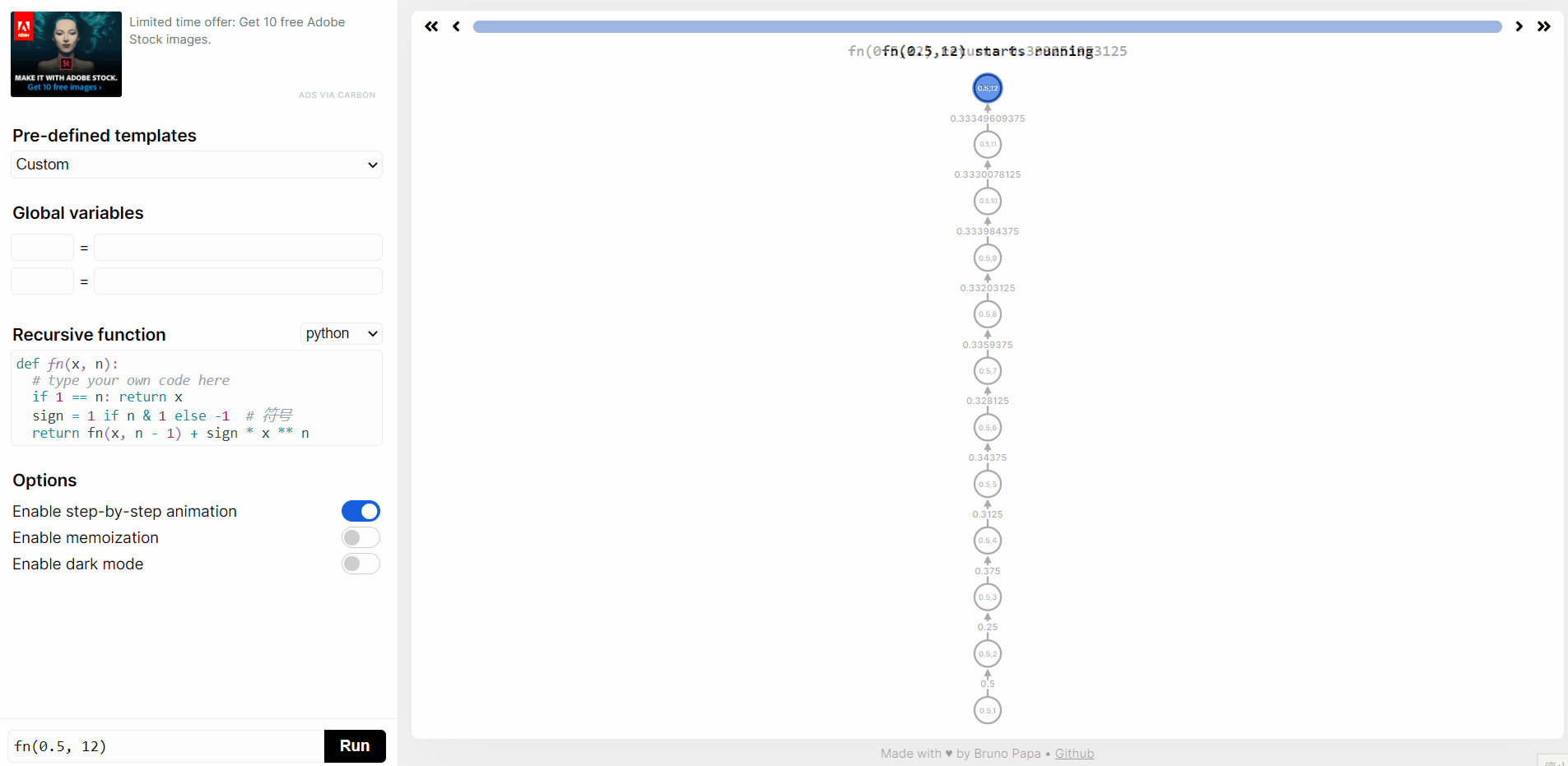
double calc_pow(double x, int n) {if (n == 0) {return 1;}return x * calc_pow(x, n - 1);}double fn(double x, int n) {if (n == 1) {return x;}int sign = n & 1 ? 1 : -1;return fn(x, n - 1) + sign * calc_pow(x, n);}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价, 偶数n | Accepted | 8 | 3 ms | 324 KB |
| 1 | 奇数n | Accepted | 5 | 2 ms | 296 KB |
| 2 | n = 1 | Accepted | 1 | 2 ms | 296 KB |
| 3 | x = 0 | Accepted | 1 | 3 ms | 364 KB |
习题10-5 递归计算Ackermenn函数
本题要求实现 Ackermenn 函数的计算,其函数定义如下:
函数接口定义:
int Ack( int m, int n );
其中m和n是用户传入的非负整数。函数Ack返回Ackermenn函数的相应值。题目保证输入输出都在长整型
范围内。
裁判测试程序样例:
#include <stdio.h>int Ack( int m, int n );int main(){int m, n;scanf("%d %d", &m, &n);printf("%d\n", Ack(m, n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
2 3
输出样例:
9
解题思路:本题已经给出递推式,因此找到递归链条和递归出口即可。
- 递归出口:当
m = 0时返回n + 1 - 递归链条:
- 若
n = 0 && m > 0则ack(m, n) = ack(m - 1, 1) - 若
n > 0 && m > 0则ack(m, n) = ack(m - 1, ack(m, n - 1))在 https://recursion.vercel.app/ 网站提交下图中 python 代码,然后点击 RUN,就可以看到
ack(2, 3)递归函数执行过程。
- 若
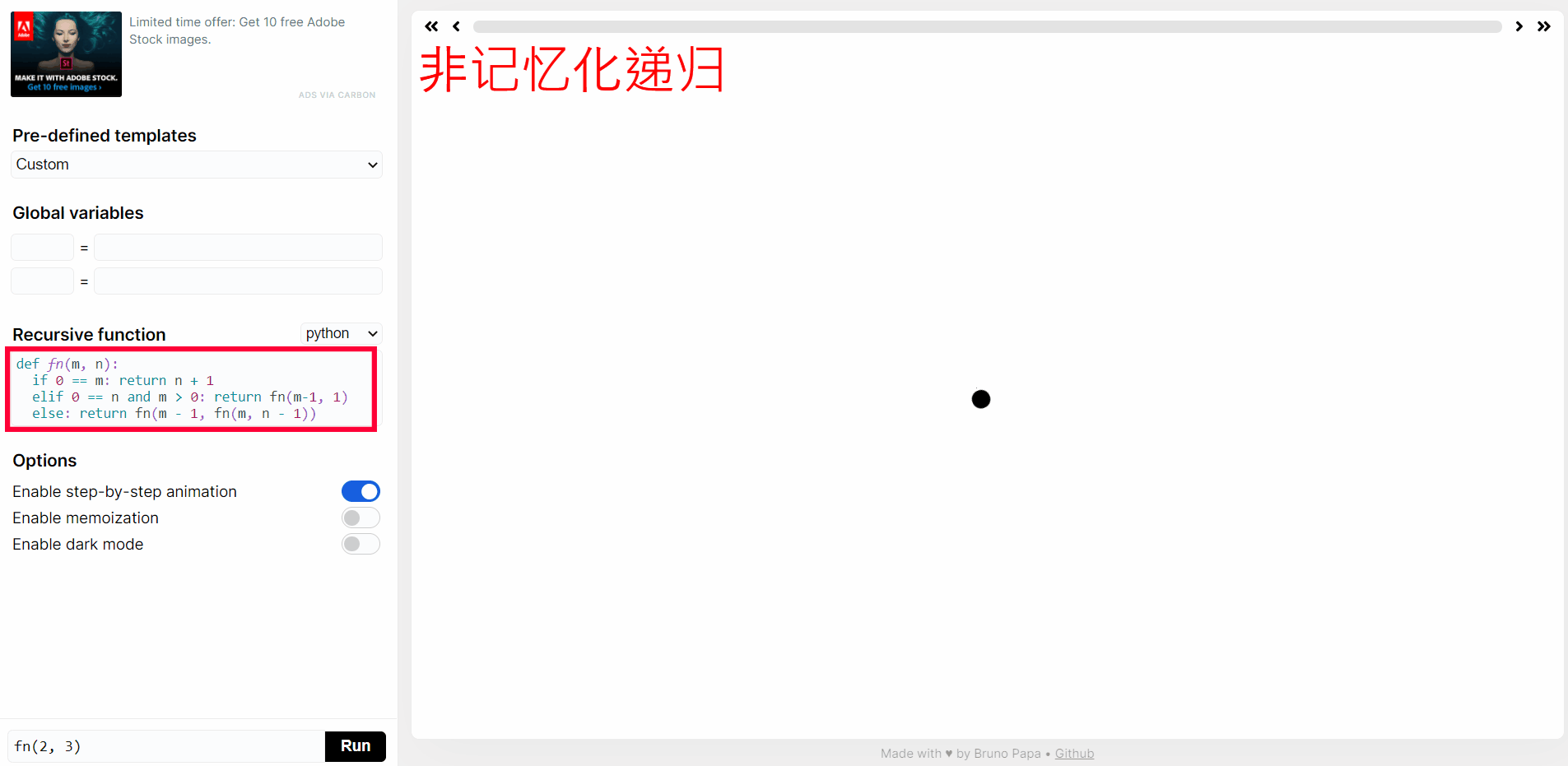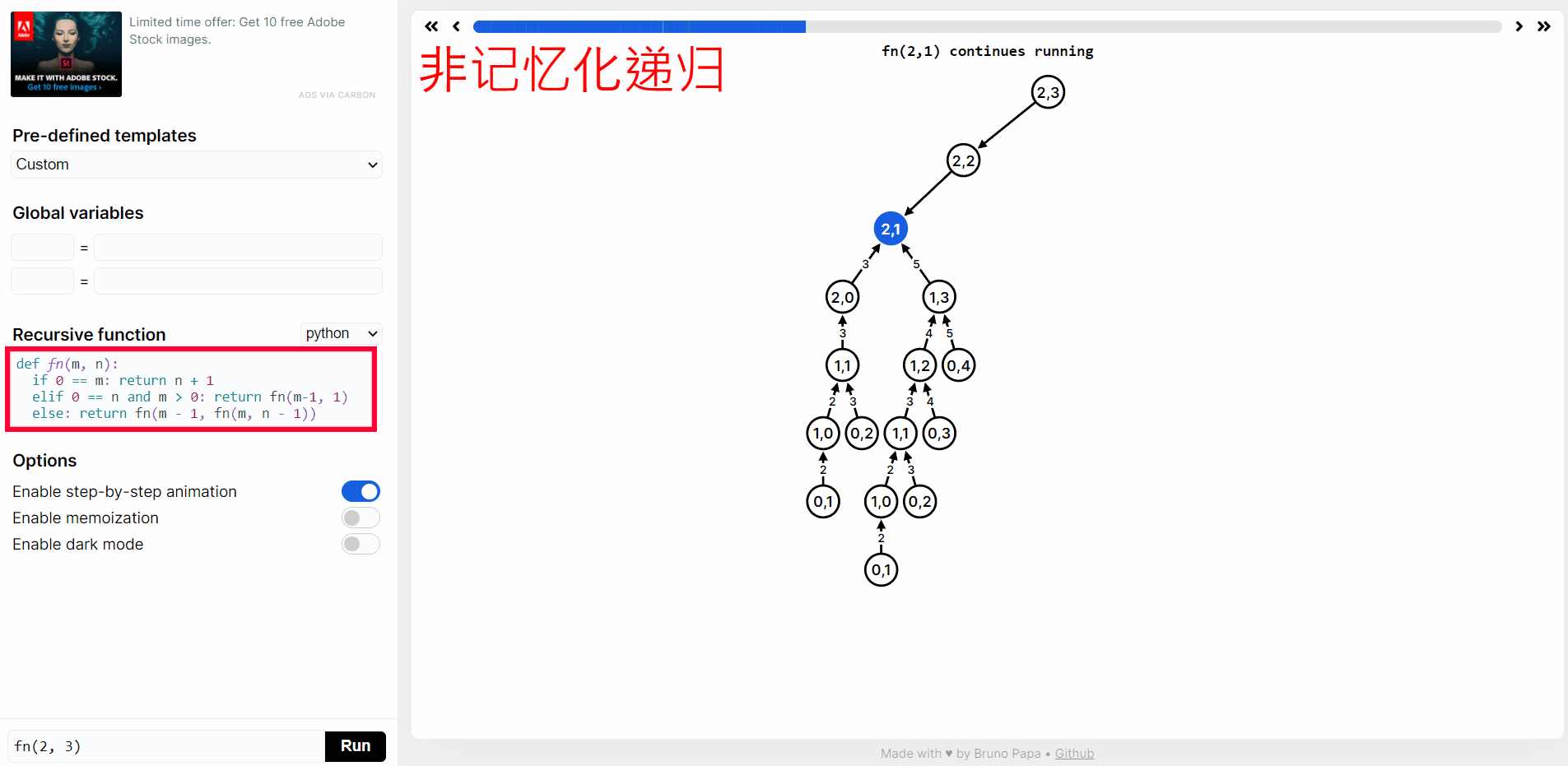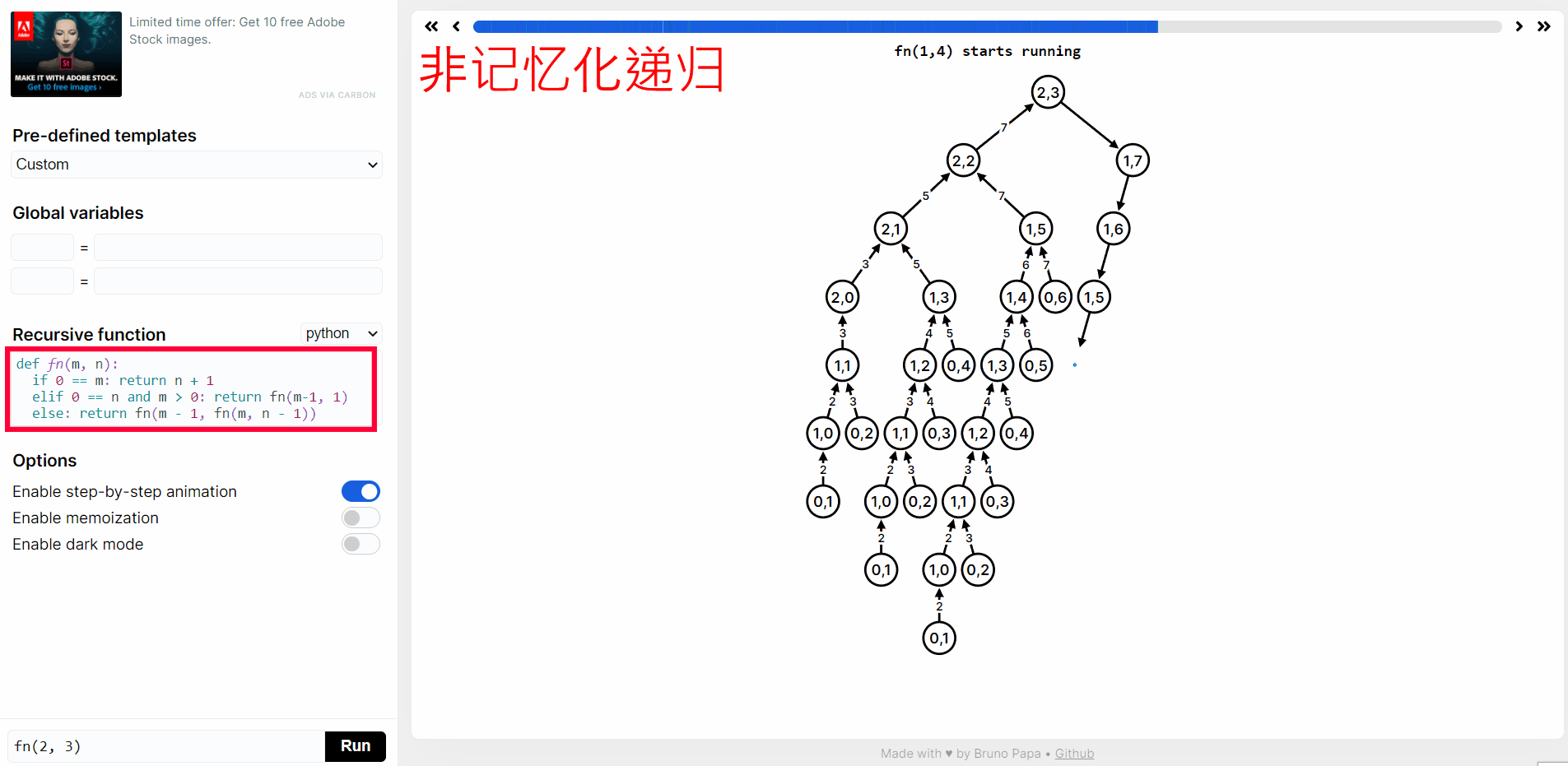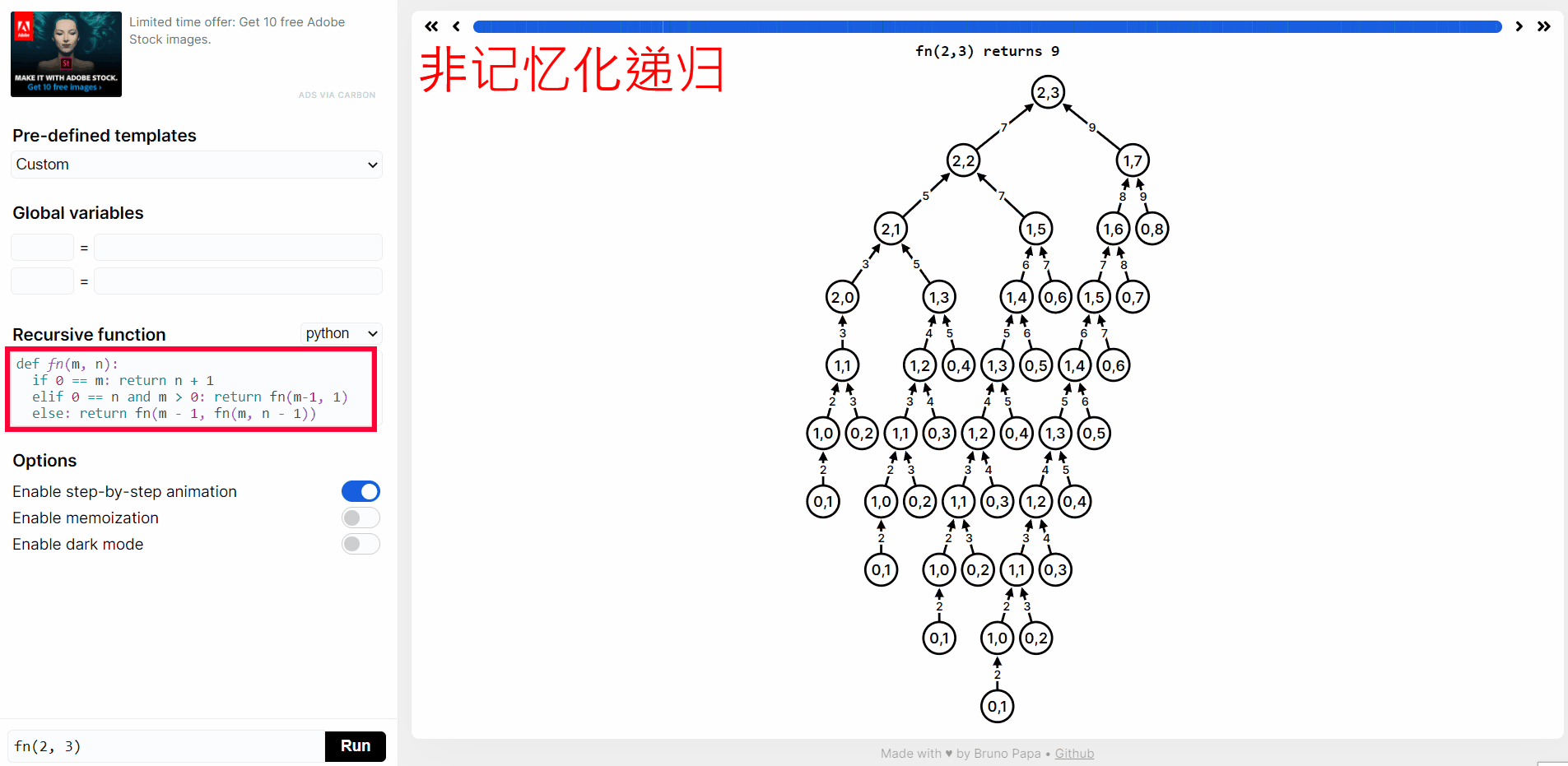
实际上上面有很多重复计算,我们点击 Enable memoization 进行记忆化递归: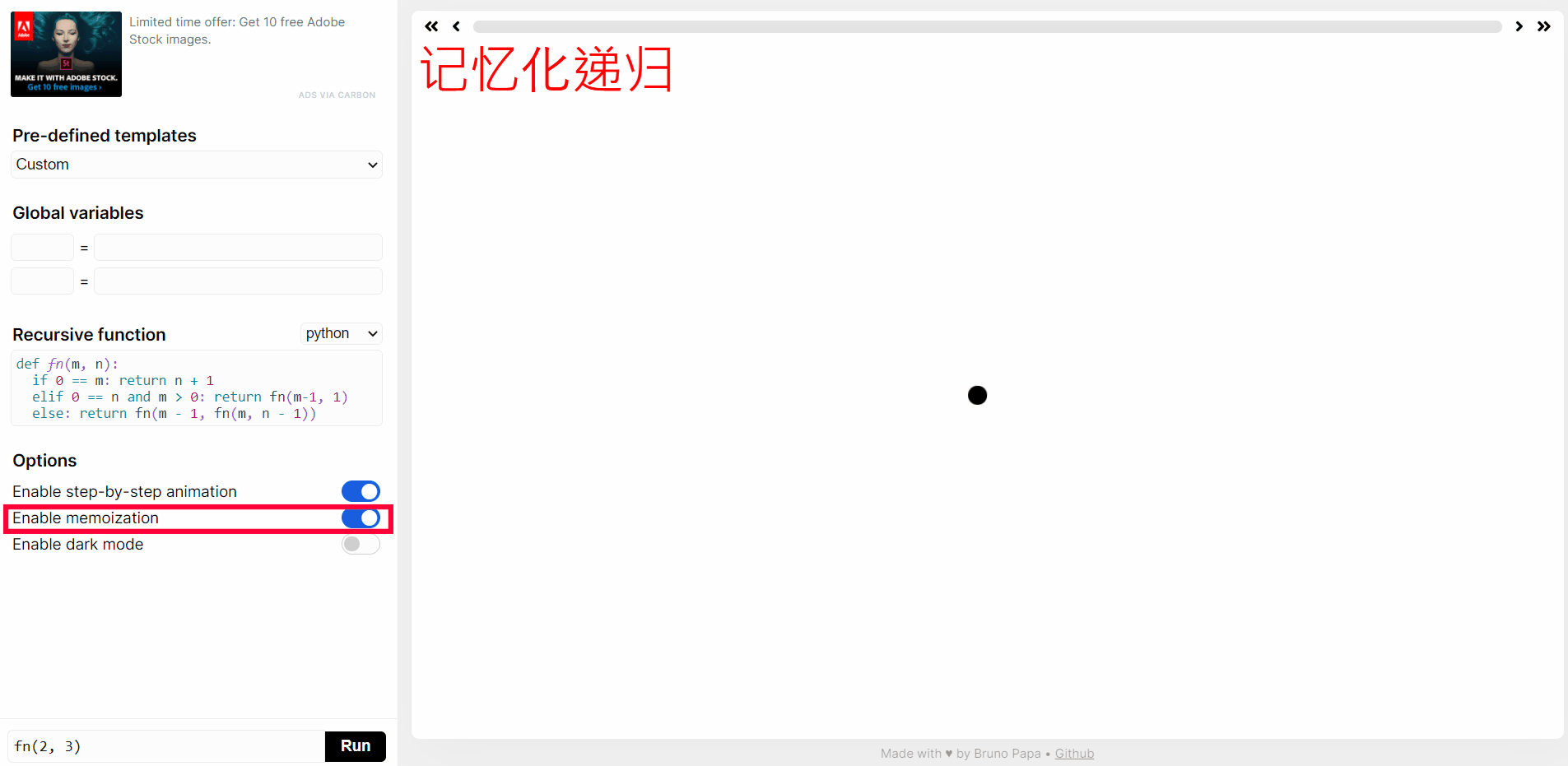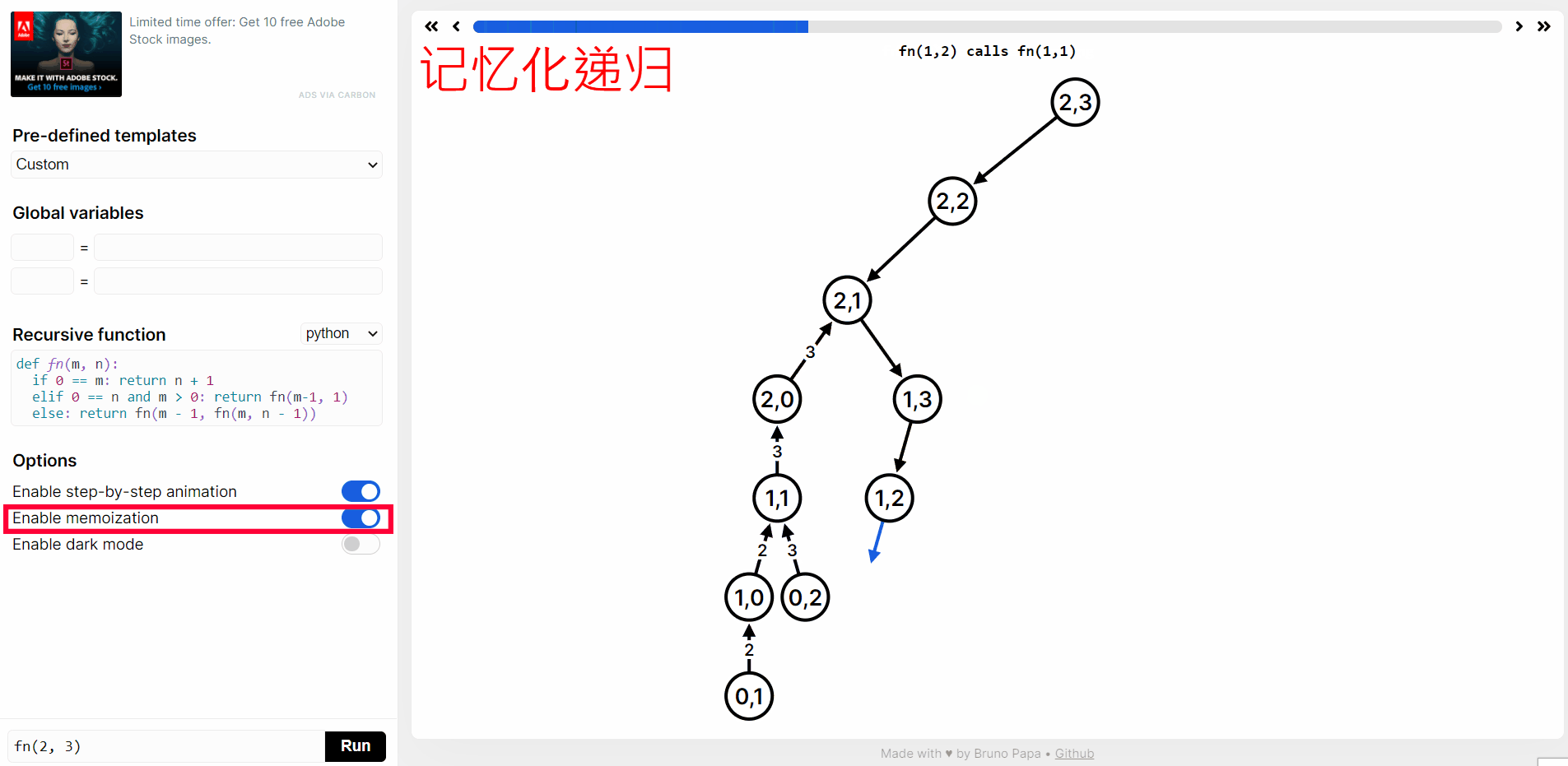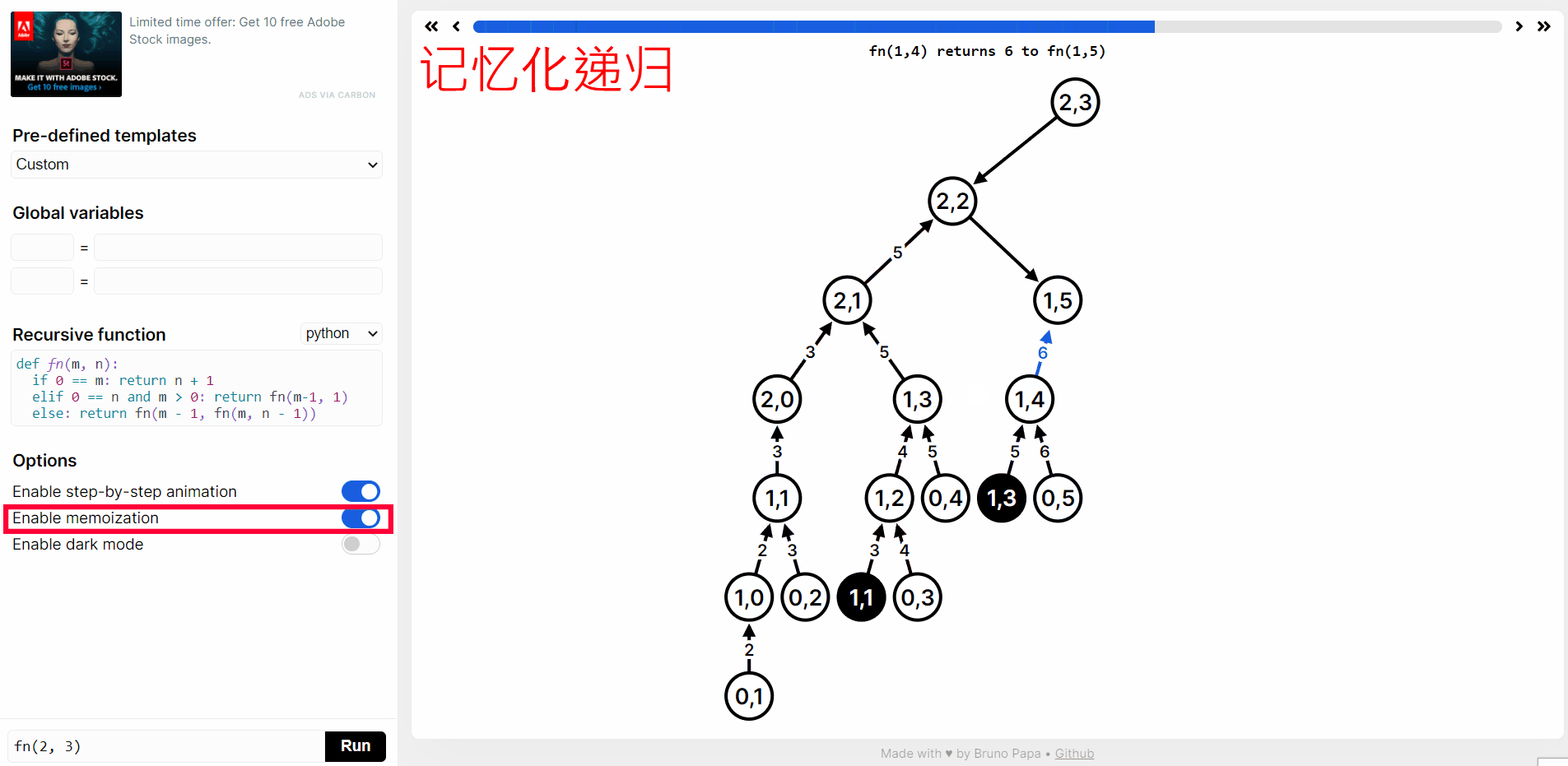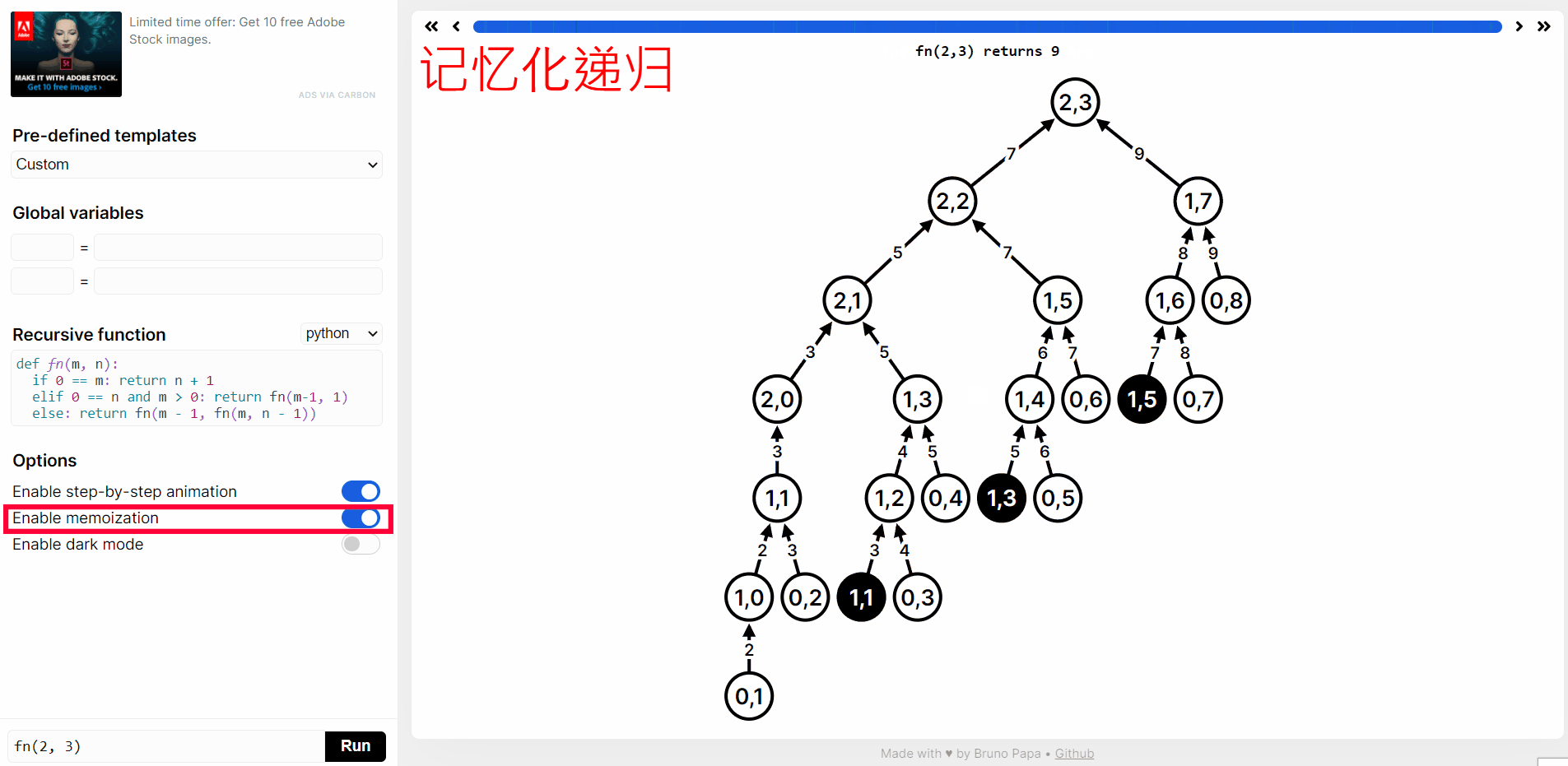
int Ack(int m, int n) {if (0 == m) {return n + 1;} else if (0 == n && m > 0) {return Ack(m - 1, 1);}return Ack(m - 1, Ack(m, n - 1));}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价, m,n均为正 | Accepted | 9 | 3 ms | 272 KB |
| 1 | m为0 | Accepted | 2 | 3 ms | 224 KB |
| 2 | n为0 | Accepted | 2 | 3 ms | 256 KB |
| 3 | 均为0 | Accepted | 2 | 3 ms | 384 KB |
习题10-6 递归求Fabonacci数列
本题要求实现求 Fabonacci 数列项的函数。Fabonacci 数列的定义如下:_
函数接口定义:
int f( int n );
函数f应返回第n个Fabonacci数。题目保证输入输出在长整型范围内。建议用递归实现。
裁判测试程序样例:
#include <stdio.h>int f( int n );int main(){int n;scanf("%d", &n);printf("%d\n", f(n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
6
输出样例:
8
解题思路:本题是经典递归题目(记忆化递归过渡到动态规划的入门案例)
语雀内容
本题为符合递归,写出递归(非记忆化)代码如下:
int f(int n) {if (0 == n) return 0;else if (1 == n) return 1;return f(n - 1) + f(n - 2);}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价, n超过2 | Accepted | 8 | 3 ms | 228 KB |
| 1 | n为0 | Accepted | 1 | 2 ms | 384 KB |
| 2 | n为1 | Accepted | 1 | 2 ms | 296 KB |
习题10-7 十进制转换二进制
本题要求实现一个函数,将正整数n转换为二进制后输出。
函数接口定义:
void dectobin( int n );
函数dectobin应在一行中打印出二进制的n。建议用递归实现。
裁判测试程序样例:
#include <stdio.h>void dectobin( int n );int main(){int n;scanf("%d", &n);dectobin(n);return 0;}/* 你的代码将被嵌在这里 */
输入样例:
10
输出样例:
1010
解题思路:在计算机中所有的数字都可以用二进制表示,具体见百度百科
常规方式使用循环实现「短除法」,然后用数组存储低位权值,然后再逆向输出数组内的值。
void dectobin(int n) {int bit[32], idx = 0;// 1.逆向储存do {bit[idx++] = n & 1;n >>= 1;} while (n);// 2.逆向输出for (int i = idx - 1; i >= 0; i--) {printf("%d", bit[i]);}}
但是我们使用递归函数的退栈实现逆序输出:
void dectobin(int n) {if (0 == n / 2) {printf("%d", n);return;}dectobin(n >> 1);printf("%d", n & 1); // 要在递归函数之后!}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价, 一般情况 | Accepted | 9 | 4 ms | 296 KB |
| 1 | 输出全是1 | Accepted | 2 | 3 ms | 184 KB |
| 2 | 输出只有最高位是1 | Accepted | 2 | 3 ms | 384 KB |
| 3 | 零 | Accepted | 2 | 2 ms | 196 KB |
习题10-8 递归实现顺序输出整数
本题要求实现一个函数,对一个整数进行按位顺序输出。
函数接口定义:
void printdigits( int n );
函数printdigits应将n的每一位数字从高位到低位顺序打印出来,每位数字占一行。
裁判测试程序样例:
#include <stdio.h>void printdigits( int n );int main(){int n;scanf("%d", &n);printdigits(n);return 0;}/* 你的代码将被嵌在这里 */
输入样例:
12345
输出样例:
12345
解题思路:本题解法与上面相同,都是进制表示问题。使用 do-while 循环输出数位更加方便,但是如何用递归函数实现呢?我们知道十进制正数 可以写成
。也就是递推式
。
- 递归终点:当
时就是边界条件,此时打印
即可(此处包含
0-9的数) - 递归链条:即递推式
,下一轮即求解
的递推式。 :::info Q:怎么在递归过程中打印输出呢?
A:由于上面c是最低权值,因此我们每次取出数字与预期打印输出顺序相反,所以我们在求解出每位权值后通过函数退栈返回实现“逆序”输出。如下图向上返回箭头所示。
另一种方式就是直接求解最高位的权值进行输出,不过此时要进行判断最高位位权是多少,例如12345的最高位权为,取出对应最高位权值就是
;然后次高位位权为
,取出对应最高位权值就是
;如此往后到位权为
1时就是结束条件。 :::
| Case | Hint | Result | Score | Run Time | Memory | | —- | —- | —- | —- | —- | —- | | 0 | sample等价 | Accepted | 10 | 2 ms | 188 KB | | 1 | 只有1位 | Accepted | 3 | 3 ms | 200 KB | | 2 | 零 | Accepted | 2 | 4 ms | 188 KB |void printdigits(int n) {if (0 == n / 10) {printf("%d\n", n);return;}printdigits(n / 10);printf("%d\n", n % 10); // 注意为什么打印在调用函数之后?而不是之前?}

