- 练习5-3 数字金字塔">练习5-3 数字金字塔
- 习题5-2 使用函数求奇数和">习题5-2 使用函数求奇数和
- 习题5-4 使用函数求素数和">习题5-4 使用函数求素数和
- 习题5-5 使用函数统计指定数字的个数">习题5-5 使用函数统计指定数字的个数
- 习题5-6 使用函数输出水仙花数">习题5-6 使用函数输出水仙花数
- 习题5-7 使用函数求余弦函数的近似值">习题5-7 使用函数求余弦函数的近似值
- 习题6-2 使用函数求特殊 a 串数列和">习题6-2 使用函数求特殊 a 串数列和
- 习题6-3 使用函数输出指定范围内的完数">习题6-3 使用函数输出指定范围内的完数
- 习题6-5 使用函数验证哥德巴赫猜想">习题6-5 使用函数验证哥德巴赫猜想
- 习题6-6 使用函数输出一个整数的逆序数">习题6-6 使用函数输出一个整数的逆序数
- 习题10-1 判断满足条件的三位数">习题10-1 判断满足条件的三位数
练习5-3 数字金字塔
本题要求实现函数输出n行数字金字塔。
函数接口定义:
void pyramid( int n );
其中n是用户传入的参数,为[1, 9]的正整数。要求函数按照如样例所示的格式打印出n行数字金字塔。注
意每个数字后面跟一个空格。
裁判测试程序样例:
c#include <stdio.h>void pyramid( int n );int main(){int n;scanf("%d", &n);pyramid(n);return 0;}/* 你的代码将被嵌在这里 */
输入样例:
5
输出样例:
12 23 3 34 4 4 45 5 5 5 5
解题思路:找到循环规律即可
void pyramid( int n ) {// 1.打印前缀空格,n -i个for (int i = 1; i <= n; i++) {for (int j = 0; j < n - i; j++) {printf(" ");}// 2.打印数字与个数for (int k = 0; k < i; k++) {printf("%d ", i);}// 3.换行putchar('\n');}}
运行结果:
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价 | Accepted | 9 | 4 ms | 384 KB |
| 1 | 最小n | Accepted | 2 | 4 ms | 256 KB |
| 2 | 次小n | Accepted | 2 | 4 ms | 256 KB |
习题5-2 使用函数求奇数和
本题要求实现一个函数,计算N个整数中所有奇数的和,同时实现一个判断奇偶性的函数。
函数接口定义:
int even( int n );int OddSum( int List[], int N );
其中函数even将根据用户传入的参数n的奇偶性返回相应值:当n为偶数时返回1,否则返回0。函数OddSum负责计算并返回传入的N个整数List[]中所有奇数的和。
裁判测试程序样例:
#include <stdio.h>#define MAXN 10int even( int n );int OddSum( int List[], int N );int main(){int List[MAXN], N, i;scanf("%d", &N);printf("Sum of ( ");for ( i=0; i<N; i++ ) {scanf("%d", &List[i]);if ( even(List[i])==0 )printf("%d ", List[i]);}printf(") = %d\n", OddSum(List, N));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
62 -3 7 88 0 15
输出样例:
Sum of ( -3 7 15 ) = 19
解题思路:根据其含义,其目的是用数组读取数据,同时主函数打印奇数,然后再次进行奇数求和。即每个数字进行两次奇数判断,注意其主函数是反着判断偶数。那么根据要求写函数即可。
int even(int n) {return !(n & 1); // 可用 n % 2 != 0}int OddSum(int *nums, int numsSize) {int sum = 0;for (int i = 0; i < numsSize; i++) {if (!even(nums[i])) {sum += nums[i];}}return sum;}
运行结果:
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价,有正负零,结果为正 | Accepted | 9 | 2 ms | 296 KB |
| 1 | 结果为负 | Accepted | 2 | 2 ms | 228 KB |
| 2 | 超过10个整数 | Accepted | 2 | 2 ms | 256 KB |
| 3 | 一个偶数 | Accepted | 2 | 2 ms | 256 KB |
习题5-4 使用函数求素数和
本题要求实现一个判断素数的简单函数、以及利用该函数计算给定区间内素数和的函数。
素数就是只能被1和自身整除的正整数。注意:1不是素数,2是素数。
函数接口定义:
int prime( int p );int PrimeSum( int m, int n );
其中函数 prime当用户传入参数p为素数时返回1,否则返回0;函数PrimeSum返回区间[m, n]内所有素数的和。题目保证用户传入的参数m≤n。
裁判测试程序样例:
#include <stdio.h>#include <math.h>int prime( int p );int PrimeSum( int m, int n );int main(){int m, n, p;scanf("%d %d", &m, &n);printf("Sum of ( ");for( p=m; p<=n; p++ ) {if( prime(p) != 0 )printf("%d ", p);}printf(") = %d\n", PrimeSum(m, n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
-1 10
输出样例:
Sum of ( 2 3 5 7 ) = 17
解题思路:首先要实现 prime 判断质数的函数接口,然后再实现区间 的质数和。
int prime( int p ) {for (int i = 2; i * i <= p; i++) {if (p % i == 0) {return 0;}}return p > 1;}int PrimeSum( int m, int n ) {int sum = 0;while (m <= n) {if (prime(m)) {sum += m;}m++;}return sum;}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价,从负到正 | Accepted | 12 | 4 ms | 316 KB |
| 1 | M==N,0 | Accepted | 2 | 4 ms | 316 KB |
| 2 | M小于N,0 | Accepted | 2 | 3 ms | 200 KB |
| 3 | M==N==素数 | Accepted | 2 | 3 ms | 320 KB |
| 4 | M和M取最大边界 | Accepted | 2 | 3 ms | 328 KB |
习题5-5 使用函数统计指定数字的个数
本题要求实现一个统计整数中指定数字的个数的简单函数。
函数接口定义:
int CountDigit( int number, int digit );
其中number是不超过长整型的整数,digit为[0, 9]区间内的整数。函数CountDigit应返回number中digit出现的次数。
裁判测试程序样例:
#include <stdio.h>int CountDigit( int number, int digit );int main(){int number, digit;scanf("%d %d", &number, &digit);printf("Number of digit %d in %d: %d\n", digit, number, CountDigit(number, digit));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
-21252 2
输出样例:
Number of digit 2 in -21252: 3
解题思路:本题就是将十进制的权值一一取出,然后判断是否等于 digit 。常见方法有将数字转换为字符串,然后统计数字字符 digit 出现次数。或者使用“取余除十”法,即依次取出低位权值。
// 1. 循环取权值int CountDigit( int number, int digit ) {// 虽然可以判断 number < 0 将其转换为正数,但是可能发生溢出,例如输入 -2147483648int cnt = 0;do {int remainder = number % 10;if (remainder < 0) remainder *= -1; // 负数变正数cnt += remainder == digit;number /= 10;} while (number);return cnt;}// 2. 转换为字符串int CountDigit( int number, int digit ) {char nums[15] = {'\0'};int n = sprintf(nums, "%d", number);int cnt = 0;for (int i = 0; i < n; ++i) {if (nums[i] - '0' == digit) ++cnt;}return cnt;}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价,number为负数 | Accepted | 7 | 22 ms | 324 KB |
| 1 | digit没有出现 | Accepted | 2 | 7 ms | 320 KB |
| 2 | #1位正数,出现 | Accepted | 2 | 16 ms | 192 KB |
| 3 | #1位负数,不出现 | Accepted | 2 | 14 ms | 172 KB |
| 4 | 全0 | Accepted | 2 | 10 ms | 292 KB |
习题5-6 使用函数输出水仙花数
水仙花数是指一个N位正整数(N≥3),它的每个位上的数字的N次幂之和等于它本身。例如:153=13+53+33。 本题要求编写两个函数,一个判断给定整数是否水仙花数,另一个按从小到大的顺序打印出给定区间(m,n)内所有的水仙花数。
函数接口定义:
int narcissistic( int number );void PrintN( int m, int n );
函数narcissistic判断number是否为水仙花数,是则返回1,否则返回0。
函数PrintN则打印开区间(m, n)内所有的水仙花数,每个数字占一行。题目保证100≤m≤n≤10000。
裁判测试程序样例:
#include <stdio.h>int narcissistic( int number );void PrintN( int m, int n );int main(){int m, n;scanf("%d %d", &m, &n);if ( narcissistic(m) ) printf("%d is a narcissistic number\n", m);PrintN(m, n);if ( narcissistic(n) ) printf("%d is a narcissistic number\n", n);return 0;}/* 你的代码将被嵌在这里 */
输入样例:
153 400
输出样例:
153 is a narcissistic number370371
解题思路:本题非 3 位数的水仙花,而是进行扩展为 
累加求和,即
。尤其是需要注意:使用
是数字的位数,但是其要求真数
,即此种方式有要求。
int narcissistic( int number ) {// 1.判断数字位数,因为没给<math.h>,所以不能用log函数int cnt = 0, n = number; // n 用于拷贝计算数字位数do {n /= 10;cnt++;} while (n);// 2.重新求和计算 digit ^ cntint sum = 0;n = number; // 重新拷贝赋值numberdo {int remainder = n % 10, product = 1;for (int i = 0; i < cnt; i++) {product *= remainder; // 最多5次,即最大9^5,不会溢出}sum += product;n /= 10;} while (n);// 3.判断返回即可return sum == number;}void PrintN( int m, int n ) {for (int i = m + 1; i < n; i++) {if (narcissistic(i)) {printf("%d\n", i);}}}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价,m另外输出 | Accepted | 12 | 8 ms | 384 KB |
| 1 | m最小,n另外输出 | Accepted | 3 | 6 ms | 316 KB |
| 2 | m==n要输出 | Accepted | 2 | 6 ms | 296 KB |
| 3 | 最大区间 | Accepted | 3 | 21 ms | 204 KB |
习题5-7 使用函数求余弦函数的近似值
本题要求实现一个函数,用下列公式求cos(x)的近似值,精确到最后一项的绝对值小于e:
函数接口定义:
double funcos( double e, double x );
其中用户传入的参数为误差上限e和自变量x;函数funcos应返回用给定公式计算出来、并且满足误差要求的cos(x)的近似值。输入输出均在双精度范围内。
裁判测试程序样例:
#include <stdio.h>#include <math.h>double funcos( double e, double x );int main(){double e, x;scanf("%lf %lf", &e, &x);printf("cos(%.2f) = %.6f\n", x, funcos(e, x));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
0.01 -3.14
输出样例:
cos(-3.14) = -0.999899
解题思路:本题就是 while 循环计算某一项值不满足要求为止,并且给出公式,直接模拟即可。但是有一些数据误差问题。
double funcos(double e, double x) {// 1.初始化第一项:肯定存在第一项,不管你 e 是否多大int sign = 1, poly = 0; // 控制符号int denominator = 1; // x ^ 0 = 0! = 1double numerator = 1, sum = 1, item = numerator / (double)denominator;// 2.循环执行条件为 fabs(item) < ewhile (fabs(item) >= e) {numerator *= x * x;poly += 2;denominator *= (poly - 1) * poly;sign *= -1;item = numerator / (double)denominator;sum += sign * item;}return sum;}
本想着 int denominator = 1; 可以在计算阶乘上快速点,以上代码在测试用例集非常大的时候超时!原因我猜多半是因为溢出!!! 超过整型上限,改为 long long int 都不可以!!最后改为 double 直接通过!
double funcos(double e, double x) {// 1.初始化第一项:肯定存在第一项,不管你e是否多大int sign = 1, poly = 0; // 控制符号double numerator = 1.0, sum = 1.0, denominator = 1.0, item = numerator / denominator;// 2.循环执行条件为 fabs(item) >= ewhile (fabs(item) >= e) {numerator *= x * x;poly += 2;denominator *= (poly - 1) * poly;sign = -sign;item = numerator / denominator;sum += sign * item;}return sum;}
| Case | Hint | Result | Score | Run Time | Memory |
|---|---|---|---|---|---|
| 0 | sample等价,计算量较小 | Accepted | 9 | 3 ms | 188 KB |
| 1 | 精度高,不可直接计算阶乘 | Accepted | 4 | 3 ms | 188 KB |
| 2 | 特殊点pi/2 | Accepted | 1 | 4 ms | 192 KB |
| 3 | 特殊点0 | Accepted | 1 | 3 ms | 184 KB |
习题6-2 使用函数求特殊 a 串数列和
给定两个均不超过9的正整数a和n,要求编写函数求a+aa+aaa++⋯+aa⋯a(n个a)之和。
函数接口定义:
int fn( int a, int n );int SumA( int a, int n );
其中函数fn须返回的是n个a组成的数字;SumA返回要求的和。
裁判测试程序样例:
#include <stdio.h>int fn( int a, int n );int SumA( int a, int n );int main(){int a, n;scanf("%d %d", &a, &n);printf("fn(%d, %d) = %d\n", a, n, fn(a,n));printf("s = %d\n", SumA(a,n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
2 3
输出样例:
fn(2, 3) = 222s = 246
解题思路:暴力做法就是根据它两个函数定义进行即可。
- 每项
,即位权是 10,对上一项×10再加上 a 即可。
- 枚举范围为
即可。实际上每项不需要专门写函数
fn(int a, int n)单独计算值,其可由上一个值再×a 获得(对于数据很小无伤大雅)。
| Case | Hint | Result | Score | Run Time | Memory | | —- | —- | —- | —- | —- | —- | | 0 | sample等价 | Accepted | 12 | 4 ms | 180 KB | | 1 | 最小a和n | Accepted | 4 | 3 ms | 192 KB | | 2 | 最大a和n | Accepted | 4 | 4 ms | 184 KB |int fn( int a, int n ) {int ret = 0;for (int i = 0; i < n; i++) {ret = ret * 10 + a;}return ret;}int SumA( int a, int n ) {int sum = 0;for (int i = 1; i <= n; i++) {sum += fn(a, i);}return sum;}// 累乘int SumA( int a, int n ) {int sum = 0, item = 0; // 提前设置为0for (int i = 1; i <= n; i++) {item = item * 10 + a;sum += item;}return sum;}
习题6-3 使用函数输出指定范围内的完数
本题要求实现一个计算整数因子和的简单函数,并利用其实现另一个函数,输出两正整数m和n(0<_m_≤_n_≤10000)之间的所有完数。所谓完数就是该数恰好等于除自身外的因子之和。例如:6=1+2+3,其中1、2、3为6的因子。
函数接口定义:
int factorsum( int number );void PrintPN( int m, int n );
其中函数factorsum须返回int number的因子和;函数PrintPN要逐行输出给定范围[m, n]内每个完数的因子累加形式的分解式,每个完数占一行,格式为“完数 = 因子1 + 因子2 + … + 因子k”,其中完数和因子均按递增顺序给出。如果给定区间内没有完数,则输出一行“No perfect number”。
裁判测试程序样例:
#include <stdio.h>int factorsum( int number );void PrintPN( int m, int n );int main(){int i, m, n;scanf("%d %d", &m, &n);if ( factorsum(m) == m ) printf("%d is a perfect number\n", m);if ( factorsum(n) == n ) printf("%d is a perfect number\n", n);PrintPN(m, n);return 0;}/* 你的代码将被嵌在这里 */
输入样例1:
1 30
输出样例1:
1 is a perfect number1 = 16 = 1 + 2 + 328 = 1 + 2 + 4 + 7 + 14
输入样例2:
7 25
输出样例2:
No perfect number
解题思路:题目最麻烦的就是边界格式的控制。所谓完数就是该数恰好等于除自身外的因子之和,但是 1 就这么特殊,它也是完数!
1单独判断将带来编码的麻烦,因为写多if太乱了。因为1是所有非1数的因子,因此可以直接输出!factorsum函数实现,由于1特殊性,那么初始化sum=1完美解决单独判断1的问题。- 区间
范围是否有完数需要用
flag变量标记。 - 格式输出:这是最头疼的一块!
- 只要是完数就有公共部分
m = 1,把这部分剥离后,其后形式就是+ i。 - 其类似用
+连接所有因子,因此不能在最后多加+,那么这个+一定是其后有因子才加上,即是判断有因子再在之前输出后追加+ i。 - 最后只有是完数才换行,不是不准换行。
```c
int factorsum( int number ) {
int sum = 0; // 这里初始化 1 原因就是少去 1 的判断
for (int i = 1; i < number; i++) {
if (number % i == 0) {
} } return sum; }sum += i;
- 只要是完数就有公共部分
void PrintPN( int m, int n ) { int flag = 0; // 假设无完数 while (m <= n) { if (factorsum(m) == m) { flag = 1; // 标记有完数 printf(“%d = %d”, m, 1); // 通用部分 for (int i = 2; i < m; i++) { if (m % i == 0) { printf(“ + %d”, i); } } printf(“\n”); // 换行 } m++; } if (!flag) { printf(“No perfect number”); } }
**运行结果:**| Case | Hint | Result | Score | Run Time | Memory || --- | --- | --- | --- | --- | --- || 0 | sample1等价,左端点是完数 | Accepted | 12 | 16 ms | 316 KB || 1 | 最大范围 | Accepted | 3 | 257 ms | 276 KB || 2 | 两端点都是完数 | Accepted | 3 | 13 ms | 212 KB || 3 | sample2等价,空集 | Accepted | 1 | 195 ms | 344 KB || 4 | 只有1个6 | Accepted | 1 | 19 ms | 340 KB |<a name="CC1WU"></a># [习题6-4 使用函数输出指定范围内的Fibonacci数](https://pintia.cn/problem-sets/12/problems/311)本题要求实现一个计算Fibonacci数的简单函数,并利用其实现另一个函数,输出两正整数_m_和_n_(0<_m_≤_n_≤10000)之间的所有Fibonacci数。所谓Fibonacci数列就是满足任一项数字是前两项的和(最开始两项均定义为1)的数列。<br />函数接口定义:```cint fib( int n );void PrintFN( int m, int n );
其中函数fib须返回第n项Fibonacci数;函数PrintFN要在一行中输出给定范围[m, n]内的所有Fibonacci数,相邻数字间有一个空格,行末不得有多余空格。如果给定区间内没有Fibonacci数,则输出一行“No Fibonacci number”。
裁判测试程序样例:
#include <stdio.h>int fib( int n );void PrintFN( int m, int n );int main(){int m, n, t;scanf("%d %d %d", &m, &n, &t);printf("fib(%d) = %d\n", t, fib(t));PrintFN(m, n);return 0;}/* 你的代码将被嵌在这里 */
输入样例1:
20 100 7
输出样例1:
fib(7) = 1321 34 55 89
输入样例2:
2000 2500 8
输出样例2:
fib(8) = 21No Fibonacci number
解题思路:本题关键是递推方程:和打印格式输出。
- 求解
F(n):有两种方法,递归和递推(循环迭代),前者时间复杂度为,后者为
。由于测试用例集非常小,
早就超过区间。如下测试用例集一定不会出现超时!
PrintFN:最麻烦就是倒着求,因为m不一定是Fibonacci数,所以还是需要顺着递归求第x项是否落在区间内,即是否成立。那么枚举结束点是多少?就是最大区间
n即可。- 打印格式:由题可知需要维护
flag = 0用于判断区间是否存在Fibonacci数
- 那么为保证格式输出且最后一个字符不是空格,因此需要对第一次单独处理,然后其后输出格式基本上就是
printf(" %d", fib);即此时也可修改flag = 1。 - 另一种方式就是在最后输出的时候进行判断,
flag = 1就回退一格即\b一下即可。
- 那么为保证格式输出且最后一个字符不是空格,因此需要对第一次单独处理,然后其后输出格式基本上就是
参考代码1:递推+特例处理第一个数输出
int fib(int n) {// f(n) = f(n-1) + f(n-2)int f1 = 1, f2 = 1;for (int i = 3; i <= n; i++) {int f3 = f1; // 暂存f1f1 = f1 + f2;f2 = f3;}return f1;}void PrintFN(int m, int n) {// 暴力枚举判断 1->∞ 项fibint flag = 0; // 用于判断[m,n]区间fib存在+首次输出int f1 = 1, f2 = 0;for (int i = 3; f1 <= n; i++) {if (m <= f1 && f1 <= n) {if (0 == flag) {printf("%d", f1);flag = 1;} else {printf(" %d", f1);}}int f3 = f1; // 暂存f1f1 = f1 + f2;f2 = f3;}if (0 == flag) {printf("No Fibonacci number");}}
运行结果:
| Case | Hint | Result | Run Time | Memory |
|---|---|---|---|---|
| 0 | sample1等价,左端点是完数 | Accepted | 2 ms | 268 KB |
| 1 | sample2等价,空集 | Accepted | 2 ms | 268 KB |
| 2 | 最大范围,测试fib(1) | Accepted | 2 ms | 384 KB |
| 3 | 两端点都是F数,测试超过区间的fib | Accepted | 2 ms | 360 KB |
| 4 | 只有1个1,测试fib(2) | Accepted | 2 ms | 384 KB |
参考代码2:递归+最后输出退格符:其实退格符是掩盖,并不是真正的删除,并且在评测机哪里显示乱码??
/* 你的代码将被嵌在这里 */int fib(int n) {// f(n) = f(n-1) + f(n-2)if (n < 3) return 1; // 递归出口return fib(n - 1) + fib(n - 2);}void PrintFN(int m, int n) {// 暴力枚举判断 1->∞ 项fibint flag = 0; // 用于判断[m,n]区间fib存在int i = 1, F;do {F = fib(i);if (m <= F && F <= n) {if (0 == flag) {printf("%d", F);flag = 1;} else {printf(" %d", F);}}i++;} while (F <= n);if (0 == flag) {printf("No Fibonacci number");}}/*void PrintFN(int m, int n) {// 暴力枚举判断 1->∞ 项fibint flag = 0; // 用于判断[m,n]区间fib存在int i = 1, F;do {F = fib(i);if (m <= F && F <= n) {flag = 1;printf("%d ", F); // 向后输出空格}i++;} while (F <= n);if (0 == flag) {printf("No Fibonacci number");} else { // 退格,消除最后的空格printf("\b");}}*/
| Case | Hint | Result | Run Time | Memory |
|---|---|---|---|---|
| 0 | sample1等价,左端点是完数 | Accepted | 4 ms | 256 KB |
| 1 | sample2等价,空集 | Accepted | 4 ms | 256 KB |
| 2 | 最大范围,测试fib(1) | Accepted | 4 ms | 256 KB |
| 3 | 两端点都是F数,测试超过区间的fib | Accepted | 4 ms | 256 KB |
| 4 | 只有1个1,测试fib(2) | Accepted | 4 ms | 256 KB |
其实这两者时间复杂度根本不是一个数量级,后者数据超大会直接爆炸的!
这是动态规划的入门题目了哦,有一个可视化的递归 app,https://recursion.vercel.app/,它可以显示你的递归函数执行逻辑,允许你自定义递归函数帮你可视化,非常适合递归学习!
例如 fib 的递归函数执行 fib(5) ,递归过程如下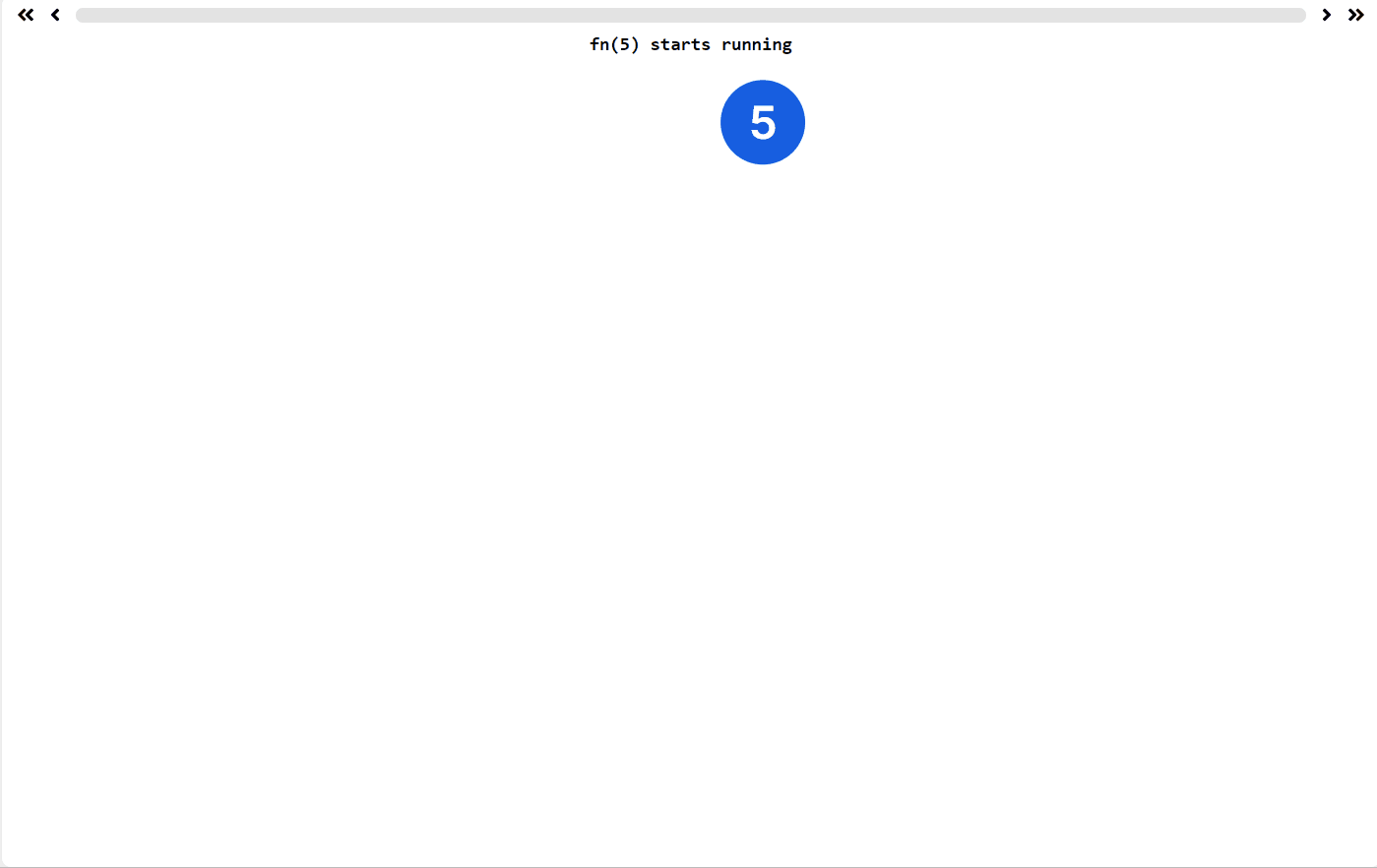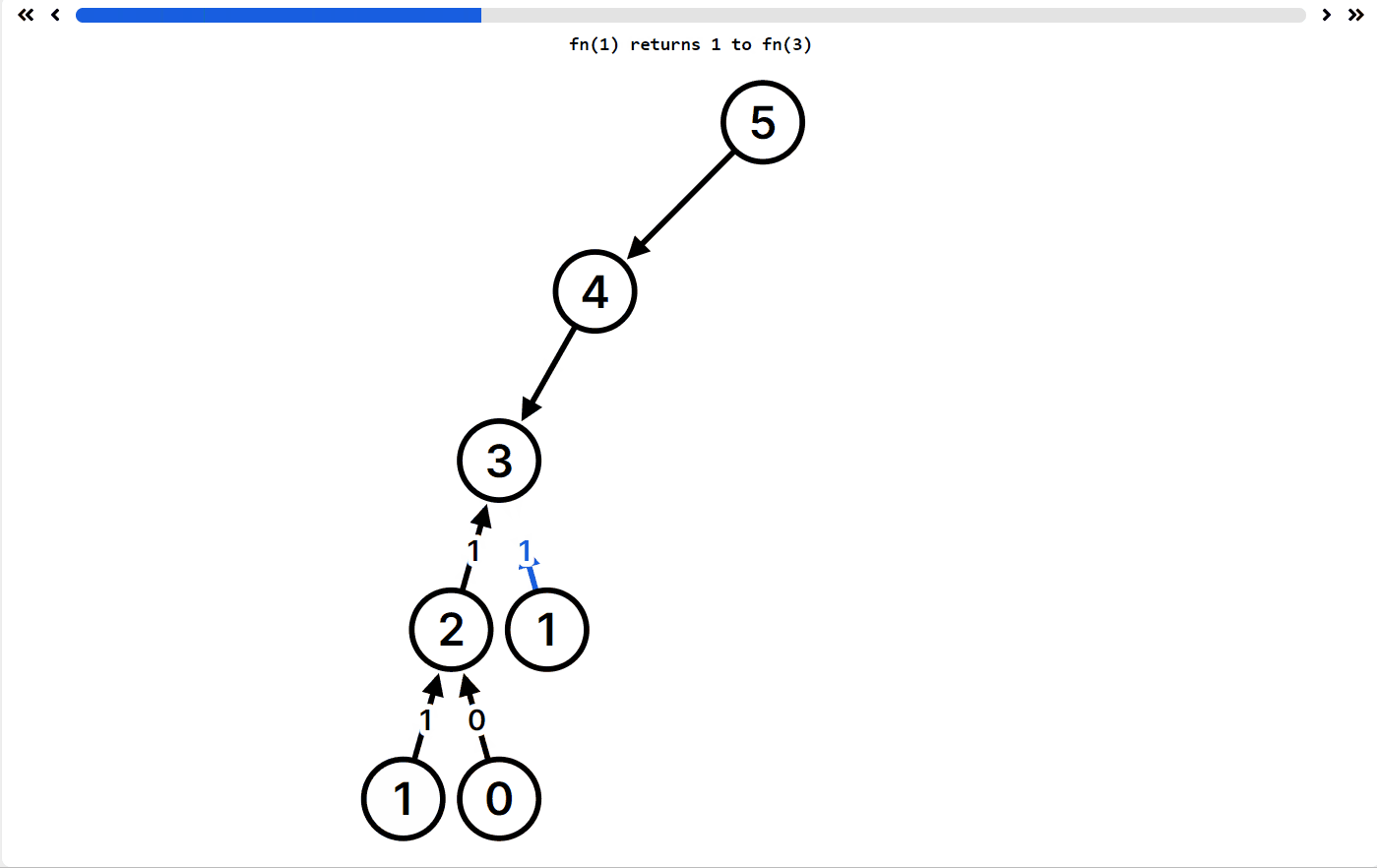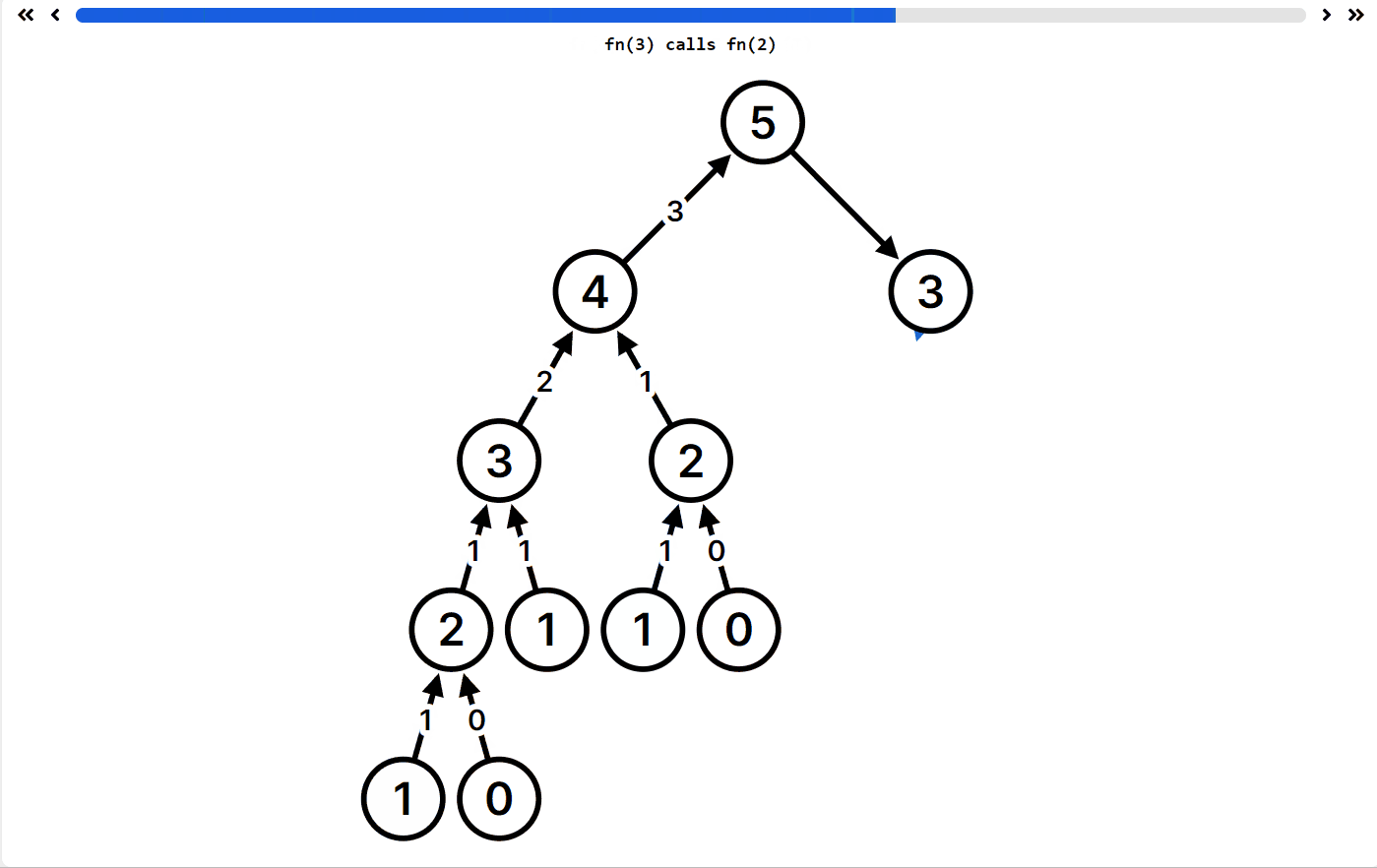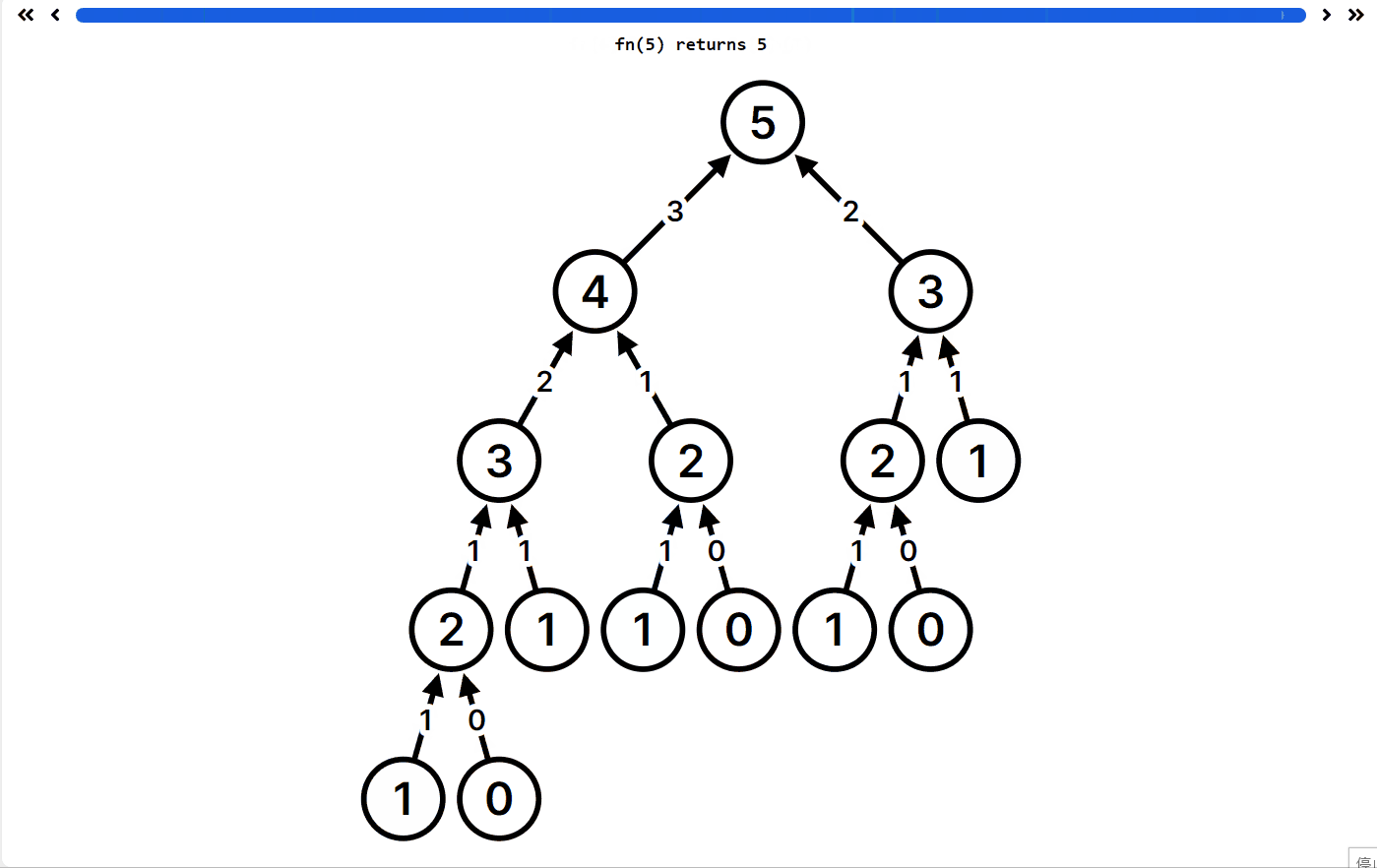
你可以看到 fib(1) 等等求解很多次,所以如果用你的代码
int fib( int n ){if(n==1){return 0;}if(n==2){return 1;} else{return fib(n-1)+fib(n-2);}}
输入 fib(100000) 跑一万年都不出结果,就是因为上面重复计算很多。因此一种方式就是保留之前计算过的值(记忆化递归就是递归过程加上一个备忘录)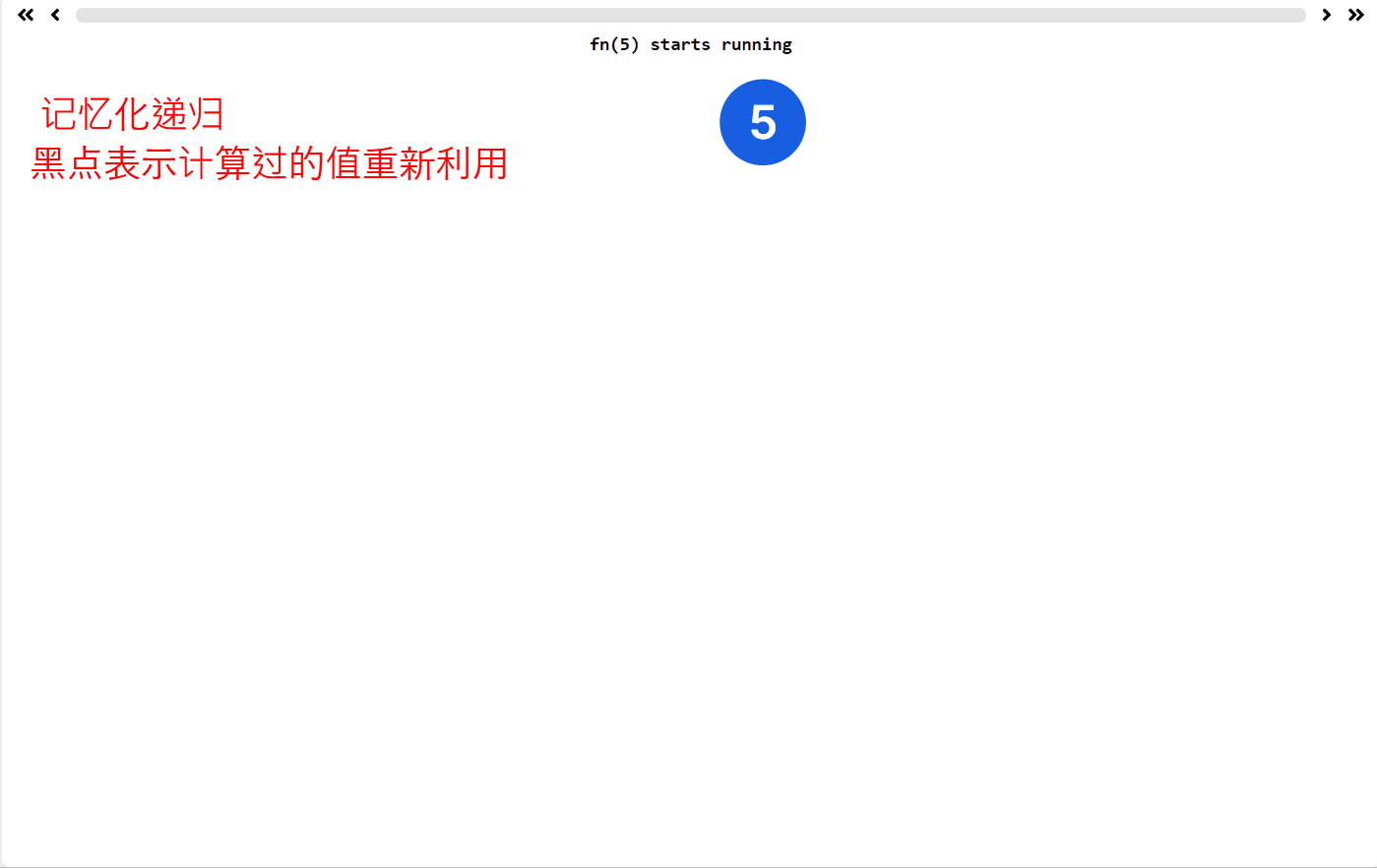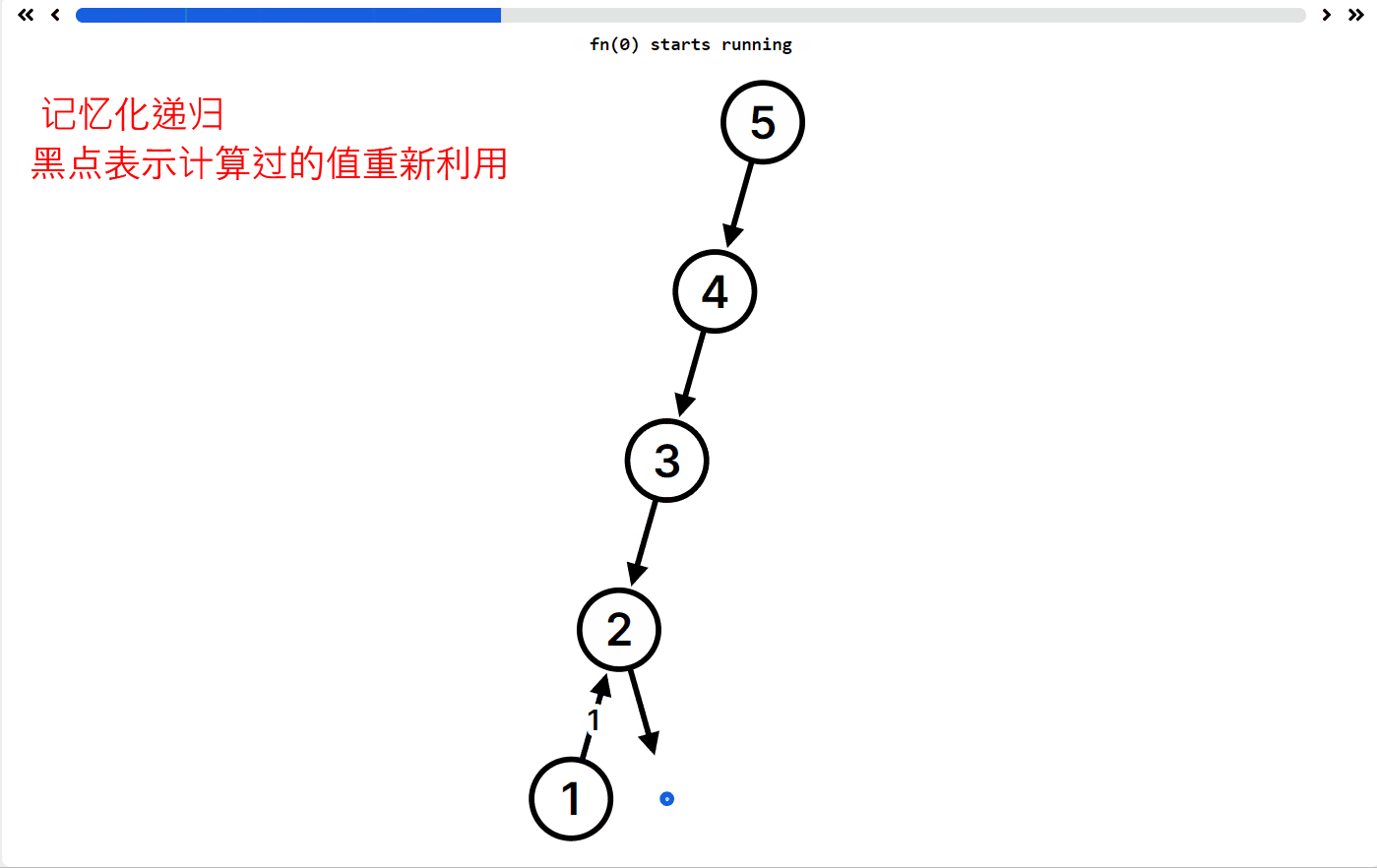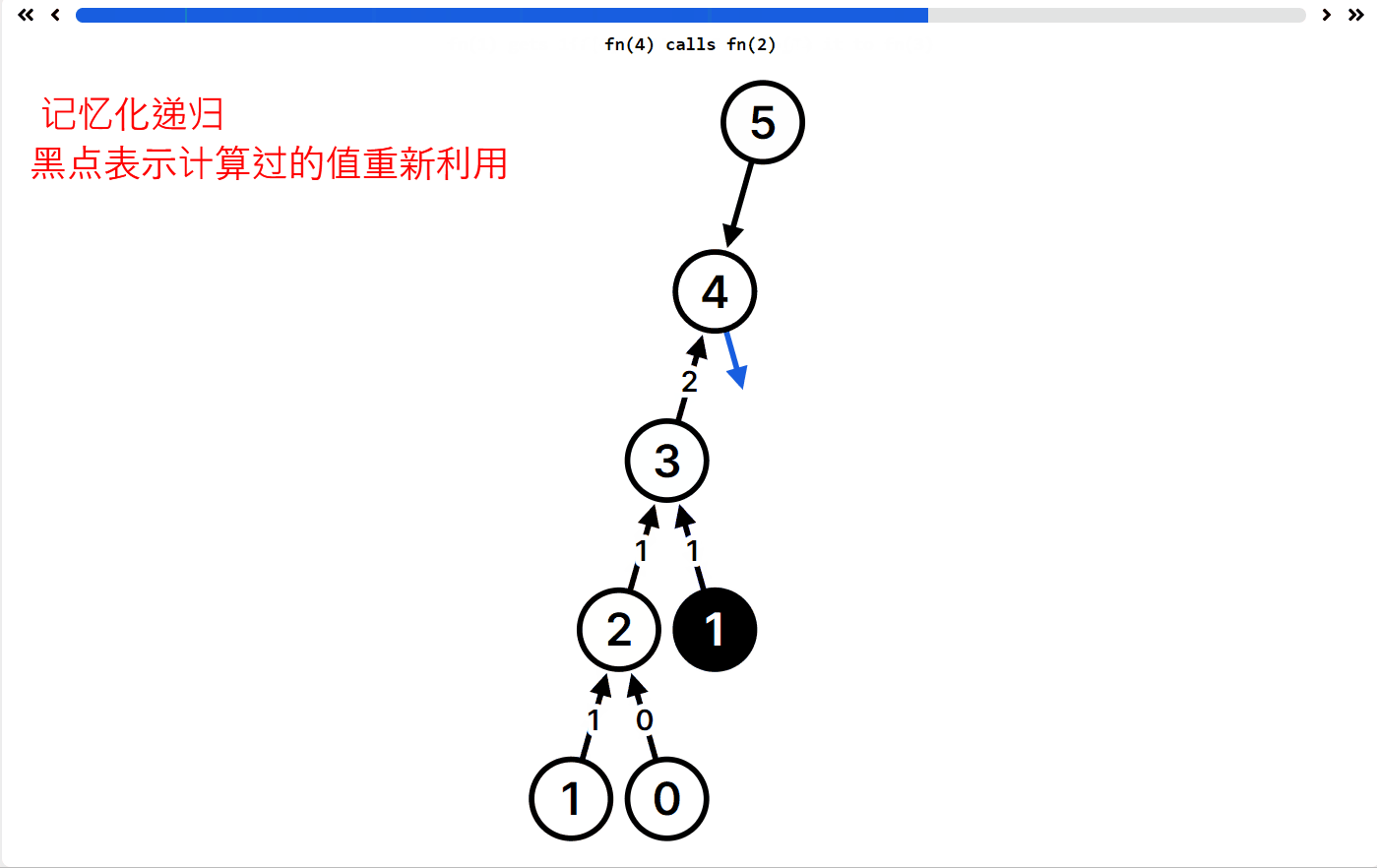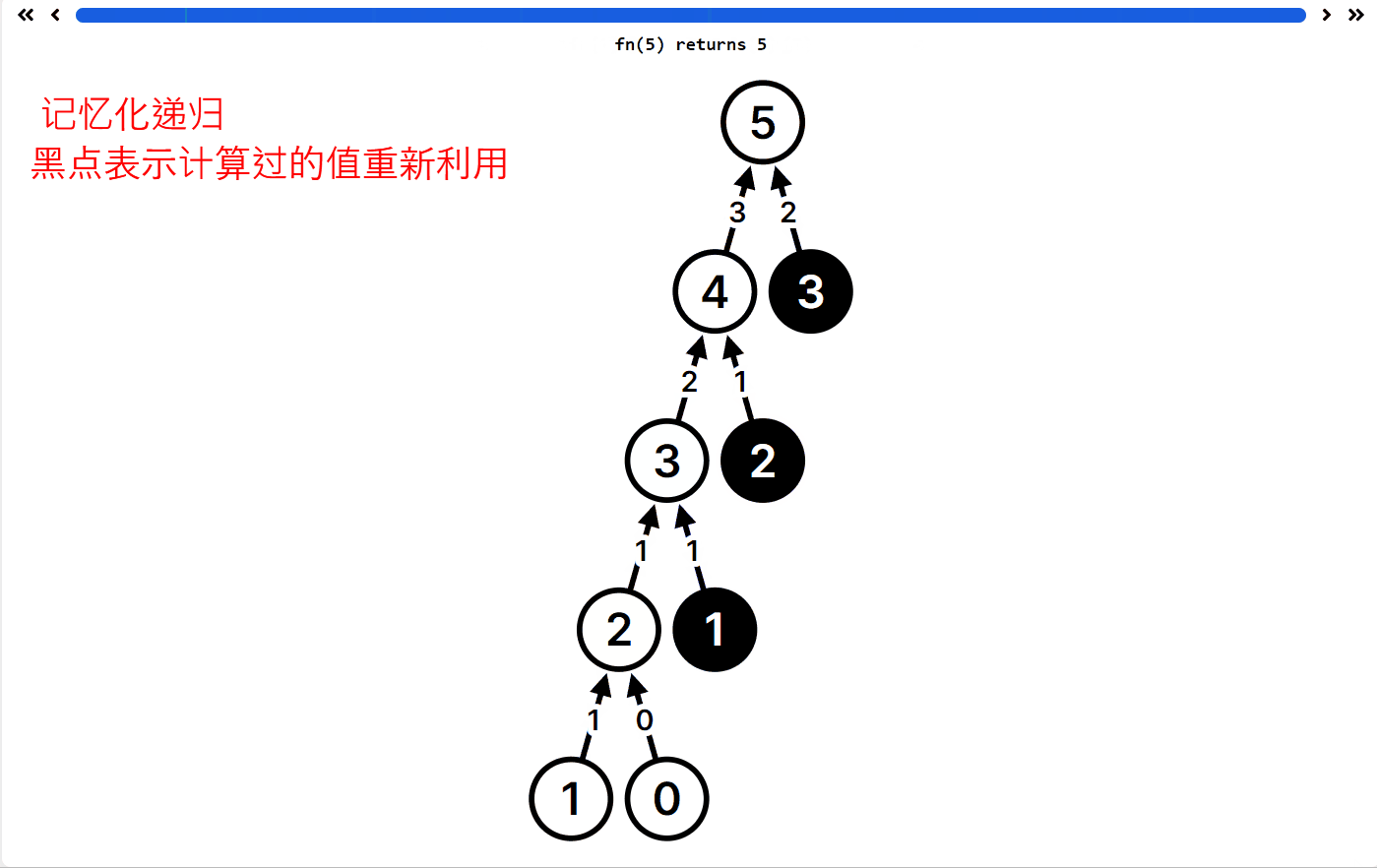
同时动态规划思想也在此开始引入,其原理和记忆化递归相同,对于「重复子问题」进行保留,也就是从小王大推导的代码:
int fib(int n) {// f(n) = f(n-1) + f(n-2)int f1 = 1, f2 = 1;for (int i = 3; i <= n; i++) {int f3 = f1; // 暂存f1f1 = f1 + f2;f2 = f3;}return f1;}
习题6-5 使用函数验证哥德巴赫猜想
本题要求实现一个判断素数的简单函数,并利用该函数验证哥德巴赫猜想:任何一个不小于6的偶数均可表示为两个奇素数之和。素数就是只能被1和自身整除的正整数。注意:1不是素数,2是素数。
函数接口定义:
int prime( int p );void Goldbach( int n );
其中函数prime当用户传入参数p为素数时返回1,否则返回0;函数Goldbach按照格式“n=p+q”输出n的素数分解,其中p≤q均为素数。又因为这样的分解不唯一(例如24可以分解为5+19,还可以分解为7+17),要求必须输出所有解中p最小的解。
裁判测试程序样例:
#include <stdio.h>#include <math.h>int prime( int p );void Goldbach( int n );int main(){int m, n, i, cnt;scanf("%d %d", &m, &n);if ( prime(m) != 0 ) printf("%d is a prime number\n", m);if ( m < 6 ) m = 6;if ( m%2 ) m++;cnt = 0;for( i=m; i<=n; i+=2 ) {Goldbach(i);cnt++;if ( cnt%5 ) printf(", ");else printf("\n");}return 0;}/* 你的代码将被嵌在这里 */
输入样例:
89 100
输出样例:
89 is a prime number90=7+83, 92=3+89, 94=5+89, 96=7+89, 98=19+79100=3+97,
解题思路:求解质数与区间验证 ,由于
可知将
p 从小到大枚举满足条件的 p 一定是最小的;因 ,当且仅当
时等号成立,即有
成立,那么
,因此可以设置
p 的枚举范围为
int prime(int p) {int sqt = (int)sqrt(p);for (int i = 2; i <= sqt; i++) {if (p % i == 0) {return 0;}}return p >= 2;}void Goldbach(int n) {// 暴力枚举 i 和 n - i 是否是质数即可// int max = sqrt(2) * n / 2;for (int i = 2; i <= n / 2; i++) {if (prime(i) && prime(n - i)) {printf("%d=%d+%d", n, i, n - i);break;}}}
运行结果:
| Case | Hint | Result | Run Time | Memory |
|---|---|---|---|---|
| 0 | sample,m是素数,有数字分解不唯一 | Accepted | 3 ms | 352 KB |
| 1 | n = m = 6 | Accepted | 3 ms | 380 KB |
| 2 | m = 2, n = 100 | Accepted | 3 ms | 368 KB |
| 3 | 检查prime(1) | Accepted | 3 ms | 296 KB |
习题6-6 使用函数输出一个整数的逆序数
本题要求实现一个求整数的逆序数的简单函数。
函数接口定义:
int reverse( int number );
其中函数reverse须返回用户传入的整型number的逆序数。
裁判测试程序样例:
#include <stdio.h>int reverse( int number );int main(){int n;scanf("%d", &n);printf("%d\n", reverse(n));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
-12340
输出样例:
-4321
解题思路:首先需要判断正负号,然后取余翻转即可。
// 迭代int reverse(int number) {int sign = 1;if (number < 0) {number = -number;sign = -1;}int ret = 0;do {int remainder = number % 10;ret = ret * 10 + remainder;number /= 10;} while (number);return ret * sign;}// 递归+静态变量int reverse(int n) {static int weight = 10; // 静态变量,当回溯时累成得到位权if(n / 10 == 0) { // 目的就是让高位直接当余数处理,否则造成多一位return n;}int ret = reverse(n / 10) + n % 10 * weight; // 注意编译器负数整除和取余操作undefined behaviourweight *= 10;return ret;}
运行结果:
| Case | Hint | Result | Run Time | Memory |
|---|---|---|---|---|
| 0 | sample,负数,逆序有前导0 | Accepted | 2 ms | 332 KB |
| 1 | 正数,无前导0,但中间有0 | Accepted | 2 ms | 296 KB |
| 2 | 负数,输入输出都有不止一个前导0 | Accepted | 3 ms | 364 KB |
| 3 | 0 | Accepted | 3 ms | 384 KB |
习题10-1 判断满足条件的三位数
本题要求实现一个函数,统计给定区间内的三位数中有两位数字相同的完全平方数(如144、676)的个数。
函数接口定义:
int search( int n );
其中传入的参数int n是一个三位数的正整数(最高位数字非0)。函数search返回[101, n]区间内所有满足条件的数的个数。
裁判测试程序样例:
#include <stdio.h>#include <math.h>int search( int n );int main(){int number;scanf("%d",&number);printf("count=%d\n",search(number));return 0;}/* 你的代码将被嵌在这里 */
输入样例:
500
输出样例:
count=6
解题思路:本题主要如何判断完全平方数的问题。
语雀内容
参考代码:
int perfectNumber(int x) {if (x < 2) return 1;long left = 1, right = x / 2;while (left <= right) {long mid = (right - left) / 2 + left;long square = mid * mid;if (x == square) { // mid * mid 溢出return 1;} else if (x > square) { // 小left = mid + 1;} else {right = mid - 1;}}return 0;}int search(int n) {int res = 0;for (int i = 101; i <= n; i++) {int cnt[10] = {0};if (perfectNumber(i)) {int x = i, max = 0;do {int remainder = x % 10;cnt[remainder]++;max = max > cnt[remainder] ? max : cnt[remainder];x /= 10;} while (x);res += max >= 2;}}return res;}
复杂度分析:
- 时间复杂度:
,其中
表示三位数范围,某一三位数
求解是否是完全平方数需要
- 空间复杂度:
| Case | Hint | Result | Score | Run Time | Memory | | —- | —- | —- | —- | —- | —- | | 0 | sample等价 | Accepted | 11 | 4 ms | 340 KB | | 1 | n = 101 | Accepted | 2 | 3 ms | 300 KB | | 2 | n = 999 | Accepted | 2 | 3 ms | 384 KB |

