1、什么是算法?试从日常生活中找3个例子,描述下它们的算法。
广义地说,为解决一个问题而采取的方法和步骤,就称为“算法”。算法是解决“做什么”和“怎么做”的问题。(C程序P15-16)
- 厨师制作菜肴,需要菜谱,菜谱上一般应说明:① 所用配料,指出为了做出顾客所指定的菜肴,应该使用哪些材料;② 操作步骤,指出有了这些原料,应按照什么样的步骤进行加工,才能做出所需的菜肴。
- 你想从北京去天津开会,首先要去买火车票,然后按时乘坐地铁到北京站,登上火车,到天津站后坐汽车到会场,参加会议。
- 要考大学,首先要填志愿表,交报名费,拿到准考证,按时参加考试,得到录取通知书,到指定学校报到注册等。
2、什么叫结构化的算法?为什么我们要用结构化的算法?
结构化算法:是由一些基本结构顺序组成的;在基本结构之间不能存在向前向后的跳转,流程的转移至存在于一个基本结构范围内(如循环中流程的跳转)(C程序P31)
一个结构化程序就是用计算机语言表示的结构化算法,用 3 中基本结构组成的程序必然是结构化的程序。这种程序便于编写、阅读、修改和维护,这就减少了程序出错的机会,提高了程序的可能性,保证了程序的质量。
3、试述 3 种基本结构的特点,请另外设计两种基本结构(符合基本结构要求的特点)。
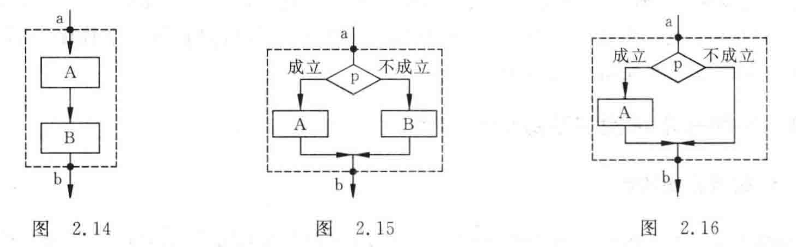
(1)顺序结构:虚线框内是一个顺序结构,先执行 A 然后再执行 B(图 2.14)。顺序结构是最简单的一种基本结构。
(2)选择结构:此结构必须包含一个判断框,根据条件 p 是否成立执行 A 框或者 B 框(图 2.15)
- 注意:根据条件往下,只能有一个可以被执行,因此另一个可以不写。(图 2.16 )
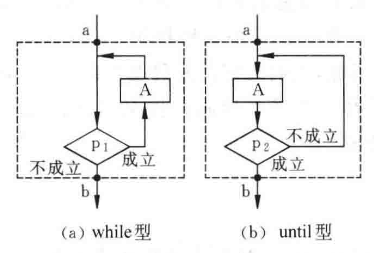
(3)循环结构:重复执行某一部分操作。共有两类。
- 当型(while型)循环结构:当给定条件 p 成立,执行 A 框操作(一定要有改变条件p的操作,否则死循环),执行后再判断 p 是否成立而继续执行 A 框。直到条件 p 不满足,从 b 点退出循环。
- 直到型(until型,对应C中
do-while):先执行 A 框,再判断条件 p 是否成立,若成立继续执行 A 框,否则从 b 点退出循环体。其最大特点就是解决前/后向性问题,比如计算数字位数。
另外两种设计如下:左:循环结构和顺序结构组合;右:多分支结构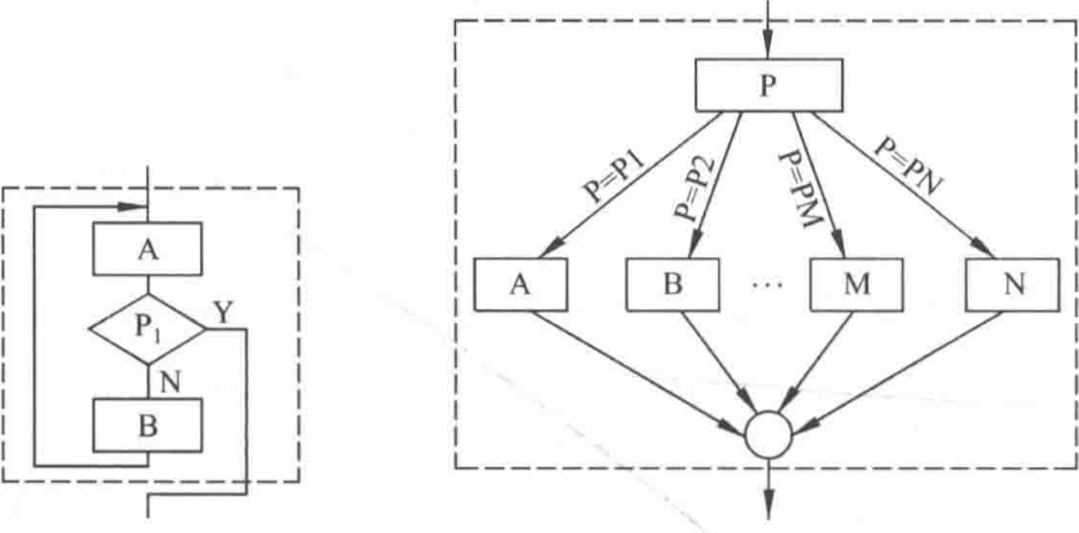
4、用传统流程图、N-S流程图、伪代码和计算机语言表示求解以下问题的解法。
(1)有两个瓶子A和B,分别放酱油和醋,要求他么互换。
- 解题思路:显然,如果有两个瓶子,肯定不能完成此任务,必须有一个空瓶 C 作为过渡。
- 流程图:
void swap1(int a, int b) { int tmp = a; a = b; b = tmp; printf(“swap1:a=%d,b=%d\n”, a, b); }
void swap2(int a, int b) { int tmp = a; a = b; b = tmp; printf(“swap2:a=%d,b=%d\n”, a, b); }
int main() { int a = 2, b = 9; // 1.swap a with b in main function int c = a; a = b; b = c; printf(“main:a=%d,b=%d\n”, a, b); // 2.call function swap1 to see what happend? swap1(a, b); printf(“swap1 callback:a=%d,b=%d\n”, a, b); // 3.call function swap2 to see what happend? swap2(&a, &b); printf(“swap2 callback:a=%d,b=%d\n”, a, b); return 0; }
编译运行::::successb12@PC:~/chapter2$ gcc -Wall ./src/swap.c -o ./bin/swap<br />b12@PC:~/chapter2$ ./bin/swap<br />main:a=9,b=2<br />swap1:a=2,b=9<br />swap1 callback:a=9,b=2<br />swap2:a=2,b=9<br />swap2 callback:a=2,b=9::::::tips这里展示在函数体内交换数字和传参(值和指针)方式交换,只是说下函数传参是传递值,即直接拷贝新的一份。所以在进行 `swap1` 是不可以修改,而 `swap2` 同样也是传值,传的就是地址的值而已,其通过在函数内部按地址找到原来的数并修改,因此是可变的。:::<a name="6ZdHk"></a>### (2)一次输入10个数,要求输出最大数。- **解题思路**:打擂台算法,首先需要两个人上去打,赢得留下继续和其他人打,最后留在台上就是王者。- 初始化:可以人为选择第一个数就是最大数,然后跟余下 9 个人对拼找出最强王者(伪代码,注意先提前知道一个数,剩余是 9 个人)。但是另一种初始化就是**虚拟**一个非常非常弱的人作为台上已经存在(C程序表示)。- **流程图:**请注意先输入一个,循环条件改为输入 9 个即可。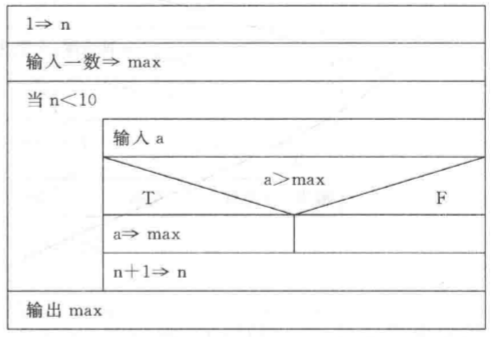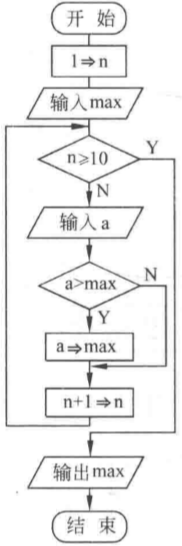- **伪代码:**
n = 1 input max // 提前读取一个数,作为最大值 while n < 10 do // 在接下来的9个数内比较大小 input a if a > max then max =a // 如果比原来的max大,那么max更新为现在的a n = n + 1 // 累加次数,一共读取9次 end do print max // 输出最大值
- **C语言:**```c#include <stdio.h>#include <limits.h>#define N 10int main() {int max = INT_MIN, x; // 初始化为int类型最小值for (int i = 0; i < N; i++) {scanf("%d", &x);if (x > max) {max = x;}}printf("the largest number is :%d\n", max);return 0;}
编译运行:
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/largest.c -o ./bin/largest
b12@PC:~/chapter2$ ./bin/largest
5
-5113545
-2147483648
456
9
23
10
4
6
800
the largest number is :800
:::
- 复杂度分析:
- 时间复杂度:
是数字个数。
- 空间复杂度:
。
- 时间复杂度:
(3)有3个数 a,b,c 要求从大到小输出。
- 解题思路:三个数共需要比较 3 次,就可分出大小,注意这与找到最大的区别,因为找到最大需要
此比较即可,而次大值还需
才可以分出大小(菜鸡互啄)。
- 流程图:
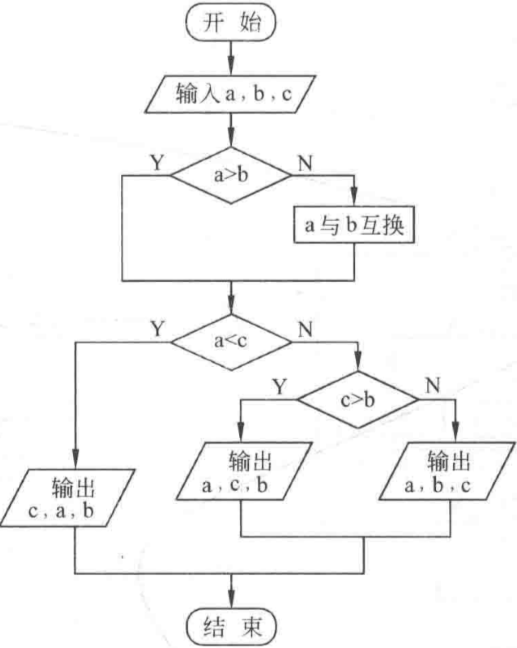
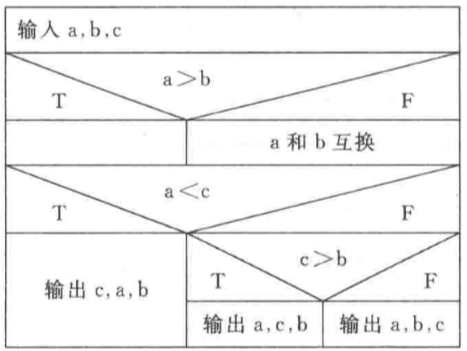
伪代码:
input a, b, cif a < b then swap(a, b) // 这里将a视为最大值替换者进行下一部比较,否则步骤更多if a < c then // a是原a和b之间最大值,a < c则大小c,a,bprint c, a, belse // 原a和b最大值大于c,那么一定a最大,关键是后两者大小尚未比较if c > b then // c > b’print a, c, belse // c < b’print a, b, cend if // 注意if和else匹配end if
C语言: ```c
include
define N 3
int main() { int a, b, c, tmp; printf(“Please input %d numbers:”, N); scanf(“%d %d %d”, &a, &b, &c); printf(“descending order of (%d, %d, %d) is “, a, b, c); // 1.if a < b then swap(a, b) to make sure a is larger if (a < b) { tmp = a; // store the value of a a = b; b = tmp; } // 2.if a < c then swap(a, c) to make sure a is larger if (a < c) { tmp = a; // store the value of a a = c; c = tmp; } // 3.a is largest, but we don’t know who is larger between b anc c if (b < c) { tmp = b; // store the value of b b = c; c = tmp; } printf(“%d, %d, %d\n”, a, b, c); return 0; }
编译运行::::successb12@PC:~/chapter2$ gcc -Wall ./src/threeSort.c -o ./bin/threeSort<br />b12@PC:~/chapter2$ ./bin/threeSort<br />Please input 3 numbers:985 46 789<br />descending order of (985, 46, 789) is 985, 789, 46:::还是同样的问题,格式化输入的毛病(空格可以跳过空白符,但是其他不可以,如果当前字符与格式字符不对, `scanf` 表示不玩了!!),可能导致问题就是未初始化问题!(因此你的输入格式只有你自己知道!):::dangerb12@PC:~/chapter2$ ./bin/threeSort<br />Please input 3 numbers:79 , 798 21<br />descending order of (79, 32730, -43323696) is 32730, 79, -43323696:::<a name="DQlyA"></a>### (4)求1+2+3+4+...100 的和- **解题思路:**累加求和,两两相加;等差数列,高斯公式。- **流程图:**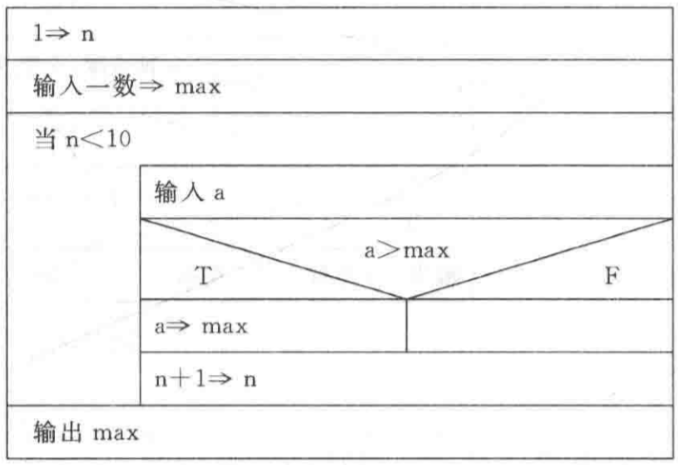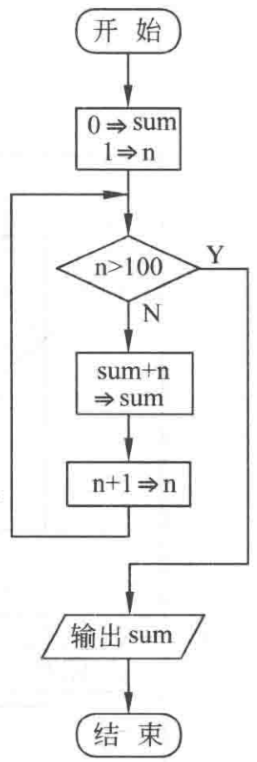- **伪代码:**
sum = 0 n = 1 while n <= 100 do sum = sum + n // 累加,没意思 n = n + 1 end do print sum
// 等差数列求和公式一步搞定: print (1+100)*100/2
- **C语言**:```c#include <stdio.h>#define N 100000int main() {int sum = 0;for (int i = 1; i <= N; i++) {sum += i;}printf("sum: %d\n", sum);}
编译运行:
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/1to100.c -o ./bin/1to100
b12@PC:~/chapter2$ time ./bin/1to100
sum: 705082704
real 0m0.009s
user 0m0.000s
sys 0m0.000s
:::
使用高斯公式求解:虽然有溢出风险!但是实际不会溢出超过 INT_MAX 范围的。
:::warning
b12@PC:~/chapter2$ gcc -Wall ./gauss.c -o ./gauss
./gauss.c: In function ‘main’:
./gauss.c:5:26: warning: integer overflow in expression of type ‘int’ results in ‘705032704’ [-Woverflow]
5 | int sum = (1 + N) / 2 * N;
| ^
b12@PC:~/chapter2$ time ./gauss
sum: 705032704
real 0m0.007s
user 0m0.000s
sys 0m0.000s
:::
上述一点都不明显,我们可以把 N 开大点,同时换 long long int 存储进行简单计时比较。
// 1.BF#include <stdio.h>#define N 10000000000.0int main() {double sum = 0;for (double i = 1; i <= N; i++) {sum += i;}printf("sum: %lf\n", sum);return 0;}// 2.Gauss#include <stdio.h>#define N 10000000000.0int main() {double sum = (1 + N) / 2 * N;printf("sum: %lf\n", sum);return 0;}
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/1to100.c -o ./bin/1to100
b12@PC:~/chapter2$ time ./bin/1to100
sum: 50000000000067862528.000000
real 0m32.026s
user 0m31.531s
sys 0m0.031s
b12@PC:~/chapter2$ gcc -Wall ./gauss.c -o ./guass
b12@PC:~/chapter2$ time ./guass
sum: 50000000005000003584.000000
real 0m0.015s
user 0m0.000s
sys 0m0.000s
:::
结果都不一样啊(正确为 50000000005000000000 ,高斯算法是否偷懒了,其实这里因为浮点数误差导致的,本例只是想简单地说明算法的优劣性而已。
- 时间复杂度:暴力求解为
,高斯公式为
。
- 空间复杂度:
。
(5)判断一个数n能否同时被3和5整除。
- 解题思路:条件就是
和
同时成立即可。
- 流程图:
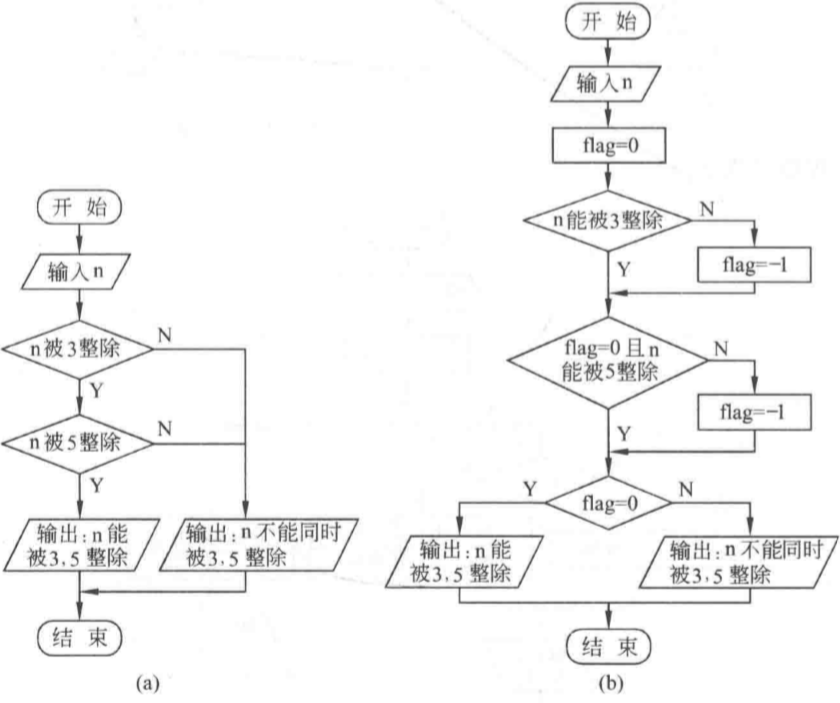
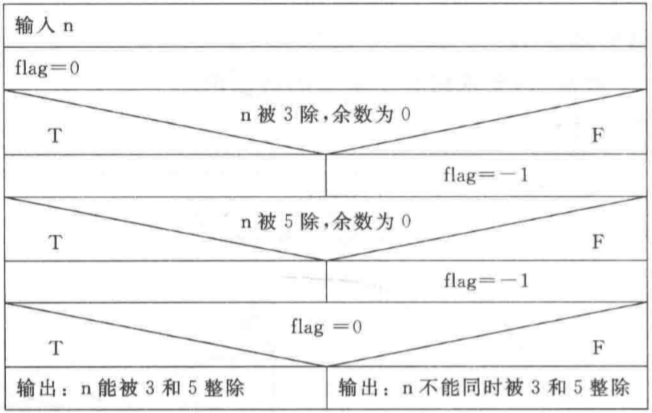 :::tips
其实这里不用经过两轮判断,直接将两个条件组合起来即可,这样只会有一个出口,但是鉴于还没学到逻辑表达式,即
:::tips
其实这里不用经过两轮判断,直接将两个条件组合起来即可,这样只会有一个出口,但是鉴于还没学到逻辑表达式,即,所以程序使用两次判断导致含有 3 个出口(左图),需要进行转换为一个出口(中间的图)才能用N-S流程图。(有点麻烦的转换)
:::
伪代码:
input nflag = 0if mod(n, 3) != 0 then flag = -1if mod(n, 5) != 0 then flag = -1if flag = 0 thenprint n "能被 3 和 5 整除"elseprint n "不能同时被 3 和 5 整除"end if
C语言: ```c
include
int main() { int n, flag = 0; printf(“Please input a number: “); scanf(“%d”, &n); if (n % 3 != 0) { flag = -1; } if (0 != n % 5) { flag = -1; } if (0 == flag) { printf(“%d 能被 3 和 5 整除\n”, n); } else { printf(“%d 不能同时被 3 和 5 整除\n”, n); } return 0; }
编译运行::::successb12@PC:~/chapter1$ gcc -Wall ./src/divide35.c -o ./bin/divide35<br />b12@PC:~/chapter1$ ./bin/divide35<br />Please input a number: 14<br />14 不能同时被 3 和 5 整除b12@PC:~/chapter1$ ./bin/divide35<br />Please input a number: 45<br />45 能被 3 和 5 整除::::::tips1. 如上如果是中文操作系统的话,WSL是可以输出中文的,因为 gcc 字符集是包含有中文的,注意使用VS2010可能出现中文乱码,尤其是sublime text3配置的gcc环境。1. 条件优化:实际上,在学习这个流程图方面确实需要一步步来,但是最好的方式可以省略。比如既然你都没法被 3 整除了,那还有被 5 整除的尝试吗?1. 即条件 2 改为: `flag != -1 && n % 5 != 0`1. 可以使用逻辑运算符一步到位::::<a name="coIob"></a>### (6)将100-200之间素数输出- **解题思路:**枚举范围内的数,逐一判断是否是质数即可。**(但是有一种更好的线性筛方法,就是由已知质数增加其倍数得到下一个质数的排除方式)**- **流程图:**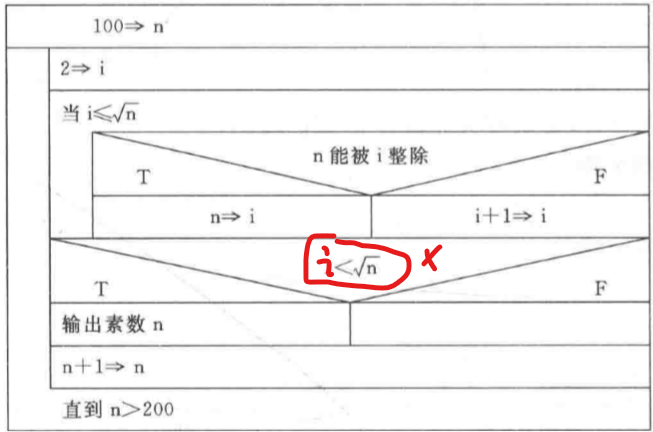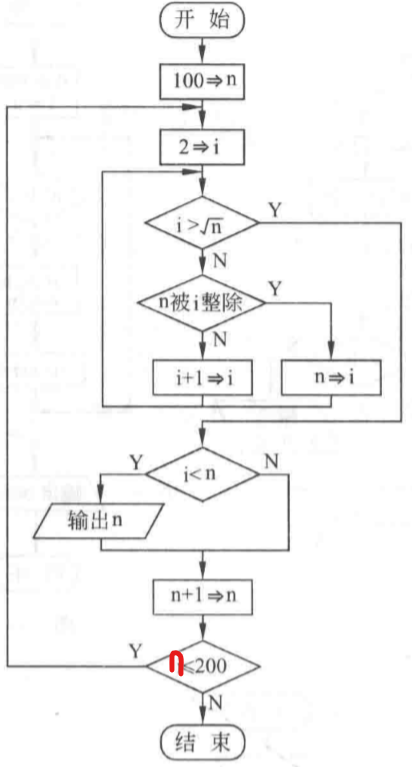:::tips**条件一**:,如何得出?假设 `n` 为合数,若存在因数 ,那么必定有另一个因数 ,成立,由 ,代入上式得 ,显然此时只可能存在 `1, n` 这对因数,由质数定义可知枚举区间  完全成立。<br />**条件二**:,如何得出?假设 `n` 为合数,存在  可知两因素大小成反比关系,那么当且仅当  是最大值。或者这样证明,若有两因数都是 ,由  与其是因数定义矛盾,故排除。注意流程图的循环边界条件以及判断质数的边界条件。- 枚举数 ,因而条件就是闭区间即可。表示方式有 或 ,关键在于最后一次判断。(作者也给出两种边界判断,需要注意都是使用 do-while 循环,代码中将会使用等价的 while 循环表示)- 质数判断边界条件:作者这里使用的是,当枚举数 n,当存在因数 i 使得 成立,那么这个 n 就不是质数,而作者流程图没给出常规的辅助判断变量而改用 `i = n` 替换,因为因数枚举范围是 ,因此让 `i = n` 实则就是让其超界起到 `flag` 作用。因而判断质数结束后,i 肯定有如下两种情况:- `i = n` :表示出现因数导致可以被 n 整除,证明不是质数。-  :此时肯定有 n 是质数成立,但是 N-S 流程图给出另外一个条件判断,即 ?- 证明:由前可知证明两个因数最大可能值就是两者相等,既有  成立,但是如果两个最大因数不等呢?比如 30 就是开根号开不尽的,那么由于向下取整算法(这里是编译器的隐式类型转换,,截取整数部分,抛弃小数)因而有 成立,其中  也是整数满足条件判断,不失一般性。但是由于循环解决, **`i++` 导致 i 的值肯定多 1,那么条件判断 **** 就是错误的,比如 ,但是 ****,此时显然 **** 不成立!**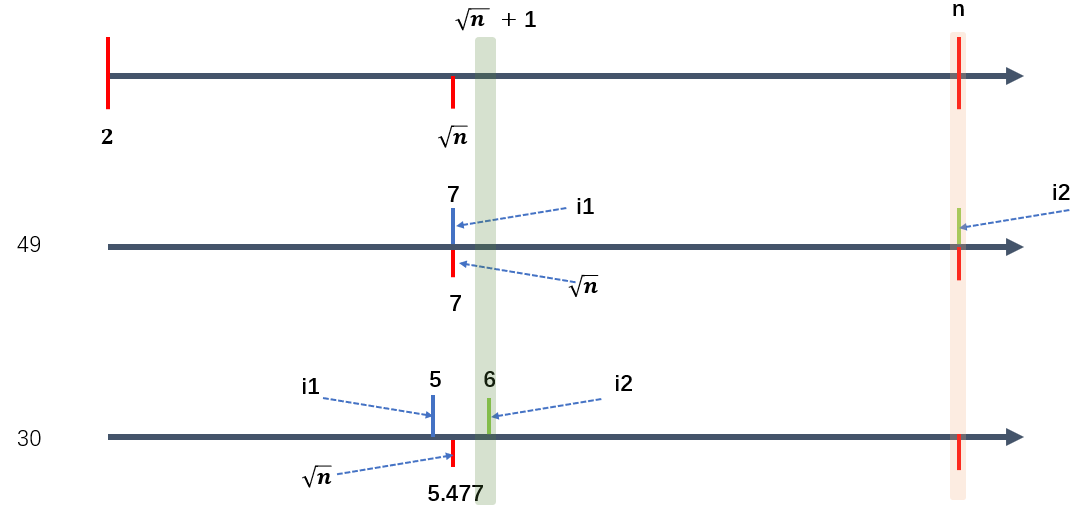<br />结论:,或者 - :一定不是质数- :肯定是质数!因为因数全部都不能整除,遍历完都超界了。:::- **伪代码:**
n = 100 // (200-100) while n <= 200 do i = 2 while i <= sqrt(n) if mod(n, i) = 0 then i = n else i = i + 1 end if end do if i < sqrt(n) then print n n = n + 1 end do
- **C语言:**```c#include <stdio.h>#include <math.h>#define START 100#define END 200int main() {for (int n = START; n <= END; n++) {int i = 2, root = sqrt(n);while (i <= root) {if (0 == n % i) {i = n;} else {i = i + 1;}}if (i != n) {printf("%d ", n);}}return 0;}
:::success
b12@PC:~/chapter1$ gcc -Wall ./src/countPrime.c -o ./bin/countPrime -lm
12@PC:~/chapter1$ time ./bin/countPrime
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
real 0m0.010s
user 0m0.000s
sys 0m0.000s
:::
- 时间复杂度:
,即为所有枚举数 n 求质数的总时间复杂度。
- 空间复杂度:
(7)求两个数m和n的最大公约数。
求最大公约数有两种方式,老祖宗的更相相损法和辗转相除法。关于证明,稍后补充。
点击查看【bilibili】
- 流程图:
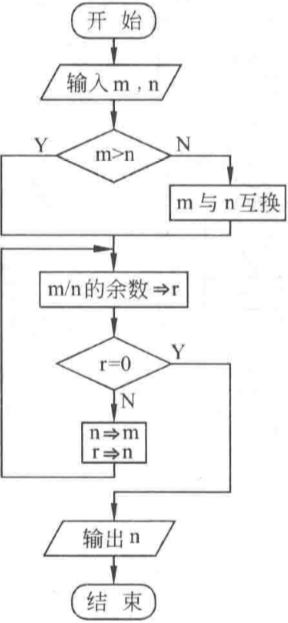
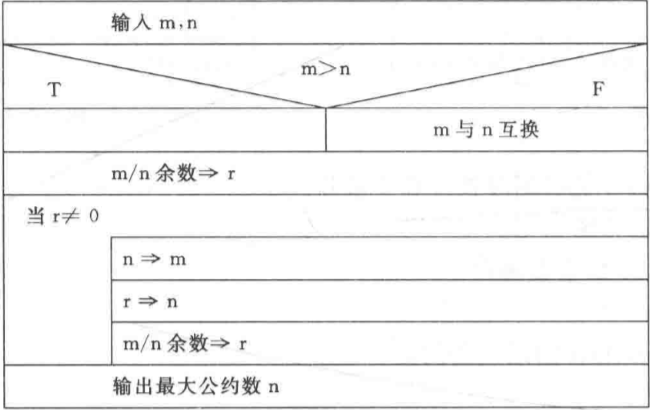
伪代码:
input m, nif m < n then swap m, n // m永远是最大值r = mod(m, n) // 取余数(辗转相除法)while r!=0 dom = n // 不断交换n = r // n当余数r = mod(m, n)end doprint n
C语言: ```c
include
int main() { int m, n, r; printf(“Please input two number: “); scanf(“%d %d”, &m, &n); printf(“The great common decomposer bewteen %d and %d is “, m, n); r = m % n; while (0 != r) { m = n; n = r; r = m % n; } printf(“%d\n”, n); return 0; }
:::successb12@PC:~/chapter2$ gcc -Wall ./src/gcd.c -o ./bin/gcd<br />b12@PC:~/chapter2$ ./bin/gcd<br />Please input two number: 5 9<br />The great common decomposer bewteen 5 and 9 is 1b12@PC:~/chapter2$ ./bin/gcd<br />Please input two number: 5 15<br />The great common decomposer bewteen 5 and 15 is 5:::<a name="xEB8c"></a>### (8)求方程式的根,分别考虑1.有两个不等的实根。2.有两个相等实根。3.没有根(复数根)- **解题思路**:这里需要考虑两种情况,但是作者却只考虑一元二次方程。要是输入的 `a=0` 程序因为除数为 0 爆炸!暂且认为是一元二次方程。求根公式步骤如下:- 先判断- ,方程有两个相等的根,即为 - ,方程有两个不相等的根,即为 - ,方程有两个不相等的复根,实部 ,虚部 ,即为 。(不要求掌握!有库函数对应求解负数根,知道就好)- **流程图:**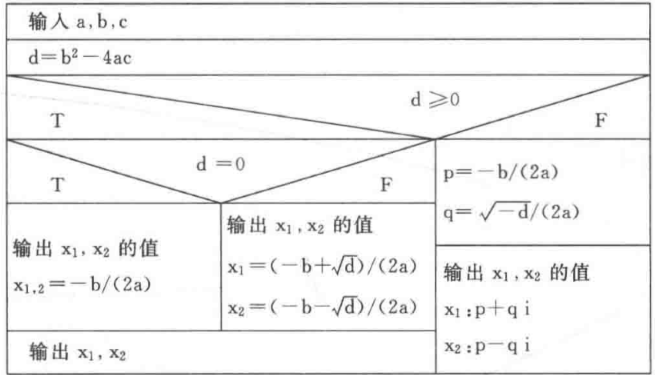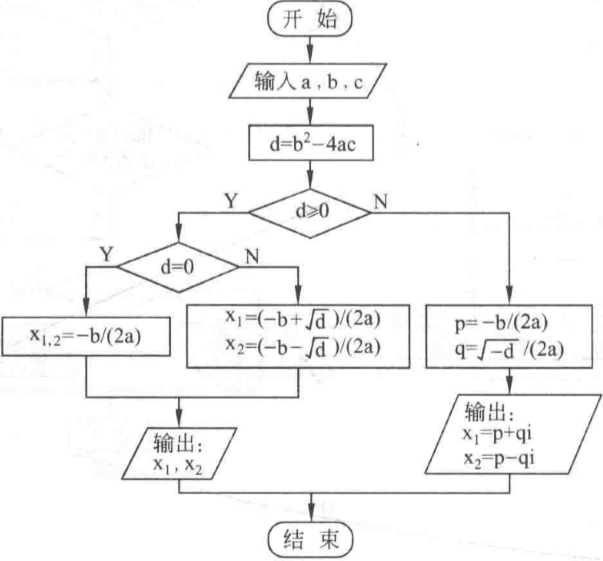- **伪代码:**
int a, b, c disc = b^2 - 4ac if disc >= 0 then if disc = 0 then x1, x2 = -b / 2a else x1 = (-b + sqrt(disc)) / 2a x2 = (-b - sqrt(disc)) / 2a end if print x1, x2 else p = -b / 2a q = sqrt(disc) / 2a print p + q, “+” p - q, “i” // 我也不知道它这里啥意思 end if
- **C语言**:(complex.h 库也可以用)```c#include <stdio.h>#include <math.h>int main() {int a, b, c;printf("Please input three numbers: ");scanf("%d %d %d", &a, &b, &c);// 1.whether Quadratic equation with one variableif (0 == a) {printf("invalid input! a = 0\n");return -1; // Error}float root, x1, x2;int delta = b * b - 4 * a * c;if (delta > 0) {root = sqrt(delta);x1 = (-b + root) / 2 * a;x2 = (-b - root) / 2 * a;printf("x1: %f, x2: %f\n", x1, x2);} else if (0 == delta) {x1 = x2 = -b / 2 * a;printf("x1 = x2: %f\n", x1);} else {root = sqrt(-delta); // negative to positivefloat p = -b / 2 * a;float q = root / 2 * a;printf("x1: %f + %fi, x2: %f - %fi\n", p, q, p, q);}return 0;}
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/equation.c -o ./bin/equation -lm
b12@PC:~/chapter2$ ./bin/equation
Please input three numbers: 1 8 15
x1: -3.000000, x2: -5.000000
b12@PC:~/chapter2$ ./bin/equation
Please input three numbers: 1 2 1
x1 = x2: -1.000000
b12@PC:~/chapter2$ ./bin/equation
Please input three numbers: 1 2 2
x1: -1.000000 + 1.000000i, x2: -1.000000 - 1.000000i
:::
- 拓展:
complex.h函数声明有以下几个,专门针对复数根求解。C99中增加了复数基本类型,一般生活在用不到,也不考。 float complex csqrtf( float complex z ); double complex csqrt( double complex z ); long double complex csqrtl( long double complex z ); long double complex csqrtl( long double complex z );
3) Computes the complex square root of z with branch cut along the negative real axis. 4) Type-generic macro: If z has type long double complex, csqrtl is called. if z has type double complex, csqrt is called, if z has type float complex, csqrtf is called. If z is real or integer, then the macro invokes the corresponding real function (sqrtf, sqrt, sqrtl). If z is imaginary, the corresponding complex number version is called. 参数要求: z - complex argument 函数返回值 If no errors occur, returns the square root of z, in the range of the right half-plane, including the imaginary axis ([0; +∞) along the real axis and (−∞; +∞) along the imaginary axis.) 案列如下:
#include <stdio.h>#include <complex.h>int main(void){double complex z1 = csqrt(-4);printf("Square root of -4 is %.1f%+.1fi\n", creal(z1), cimag(z1));double complex z2 = csqrt(conj(-4)); // or, in C11, CMPLX(-4, -0.0)printf("Square root of -4-0i, the other side of the cut, is ""%.1f%+.1fi\n", creal(z2), cimag(z2));}
编译运行:
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/complexRoot.c -o ./bin/complexRoot
b12@PC:~/chapter2$ ./bin/complexRoot
Square root of -4 is 0.0+2.0i
Square root of -4-0i, the other side of the cut, is 0.0-2.0i
:::

