 :::info
本节视频:第一章 C语言概述:程序、算法和流程图
:::
点击查看【bilibili】
:::info
本节视频:第一章 C语言概述:程序、算法和流程图
:::
点击查看【bilibili】
一个程序主要包括以下两个方面:
(1)对数据的描述:数据结构(data structure):在程序中要指定用到哪些数据以及这些数据的类型和数据的组织形式。
(2)对操作的描述:即要求计算机进行操作的步骤,也就是算法(algorithm)。
算法+数据结构=程序
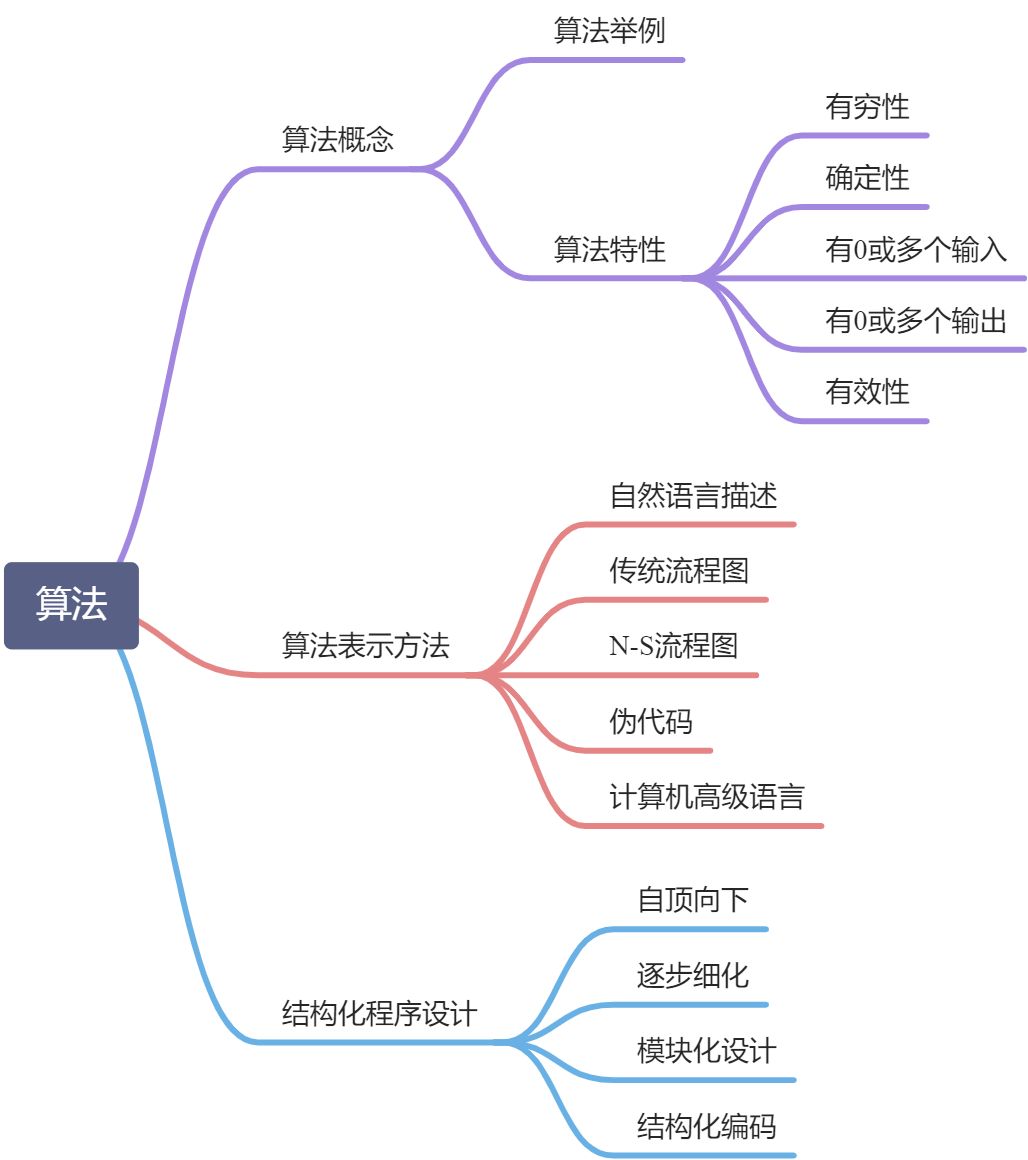
1 什么是算法?
广义地说,为解决一个问题而采取的方法和步骤,就称为“算法”。算法是解决“做什么”和“怎么做”的问题。(C程序P15)
例1:判断一个字符串是否是回文串,如 ATCCTA 或 GTCTG 都是回文串。
解决办法就是看头看尾,如果对,继续减少一个字符看直到最终看完没得看了就是回文串,否则就不是。
例2:求 ,即
问题:
一般人就是开始拿笔算,两个两个相加,进行 50 次加法得到结果,而聪明的人学过等差数列,用公式 一步到位。因而这就是人与人之间的差距。即是说解决一个问题的办法总是很多,但是一般来说,希望采用方法简单,运算步骤少的方法,效率更高。因此算法的优劣性**很重要。
计算机的算法分为两类:
- 数值运算算法:目的是求数值解,例如求方程的根、求一个函数的定积分等,都属于数值运算范围。
- 非数值运算算法:包括的面十分广泛,最常见的是用于事务管理领域,如对一批职工按姓名排序、图书检索、人事管理和行车调度管理等。
目前,计算机在非数值运算方面的应用远远超过了在数值运算方面的应用。
2 算法的特性
(1)有穷性:一个算法应包含有限的步骤,而不能是无限的。实际上“有穷性”往往指“在合理的范围之内”。(破解文件密码破解一年也不愿花2块钱买密码)
(2)确定性:算法中的每一步都应当是确定的,而不应该是含糊的、模凌两可的。算法的含义应当是唯一的,而应当产生”歧义性“。所谓”歧义性“,是指可以被理解为两种(或多种)的可能含义。
(3)有零个或多个输入:所谓输入是指在执行算法时需要从外界获取必要的信息。
(4)有一个或多个输出:算法的目的是为了求解,“解”就是输出。但算法的输出并不一定就是计算机的打印输出或屏幕输出,一个算法得到的结果就是算法的输出。没有输出的算法时没有意义的。
(5)有效性:算法中的每一个步骤都应当有效地执行,并得到正确的结果。
3 怎么样表示算法?
3.1 自然语言描述
如上判断回文串的例题就是用自然语言描述。
自然语言描述特点:
- 通俗易懂,但是文字冗长,算法较为复杂的时候就显得非常麻烦或产生歧义。
- 含义往往不太严格,要根据上下文才能判断其正确含义。
- 自然语言来描述分支和循环结构(1->100累加和)的算法不太方便。
3.2 流程图表示
流程图是用一些图框来表示各种操作。用图形表示算法,直观形象,易于理解。如下所示流程图基本结构与一个年龄判断流程图。
通过以上例子看出流程图是表示算法的较好工具。一个流程图主要包括以下几个部分:
- 表示相应操作的框
- 带箭头的流程线
- 框内外必要的文字说明
优缺点:
- 直观形象,比较清楚地显示出各个框之间的关系。
- 占用篇幅多,尤其是当算法较为复杂的时候,画流程图即使费时又不方便。
3.3 N-S 流程图
传统的流程图用流程线指出各框的执行顺序,对流程线的使用没有严格的要求限制。因而可以乱指,导致流程图标的毫无规律,阅读时要耗费大量的力气。为了提高算法的质量(表示质量),使算法的设计和阅读方便,必须限制箭头的滥用,即不允许无规律地使流程随意转向,只能顺序地执行下去。
N-S图,也被称为盒图或N-S图(Nassi Shneiderman图)。是结构化编程中的一种可视化建模。1972年,美国学者I.Nassi 和 B.Shneiderman提出了一种在流程图中完全去掉流程线,全部算法写在一个矩形框内,在框内还可以包含其他框的流程图形式(也正因为这种嵌套关系,手画的对齐和修改很难!),即由一些基本的框组成一个大的框,这种流程图又称为N-S结构流程图或盒图(box diagram)。
优缺点:(C程序P30)
- 比文字描述直观、形象、易于理解;
- 比传统流程图紧凑易画,尤其是他废除了流程线,整个算法结构是由各个基本结构按顺序组成的,N-S 流程图中的上下顺序就是执行时的顺序。
- 写算法和看算法只需从上到下进行,十分方便。
- 用 N-S 刘彻国土表示的算法都是结构化的算法(它不可能存在流程无规律地跳转,而只能自上到下地顺序进行执行)
- N-S 图几乎是流程图的同构,任何的 N-S 图都可以转换为流程图,而大部分的流程图也可以转换为N-S图。其中只有像
goto指令或是C语言中针对循环的break及continue指令无法用 N-S 图表示。 - N-S 图要求必须一个出口,当含有多个出口就需要改变!
3.4 流程图的三种基本结构
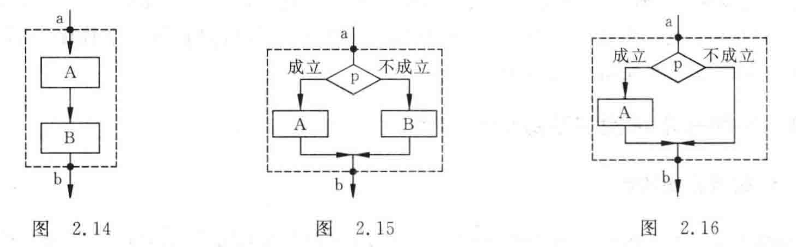
(1)顺序结构:虚线框内是一个顺序结构,先执行 A 然后再执行 B(图 2.14)。顺序结构是最简单的一种基本结构。
(2)选择结构:此结构必须包含一个判断框,根据条件 p 是否成立执行 A 框或者 B 框(图 2.15)
- 注意:根据条件往下,只能有一个可以被执行,因此另一个可以不写。(图 2.16 )
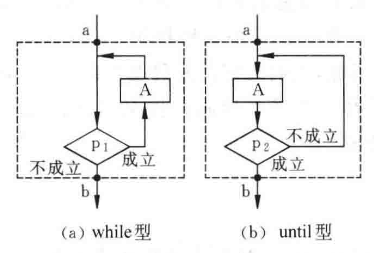
(3)循环结构:重复执行某一部分操作。共有两类。
- 当型(while型)循环结构:当给定条件 p 成立,执行 A 框操作(一定要有改变条件p的操作,否则死循环),执行后再判断 p 是否成立而继续执行 A 框。直到条件 p 不满足,从 b 点退出循环。
- 直到型(until型,对应C中
do-while):先执行 A 框,再判断条件 p 是否成立,若成立继续执行 A 框,否则从 b 点退出循环体。其最大特点就是解决前/后向性问题,比如计算数字位数。
而 N-S 流程图就非常简单:
三种流程图的共同特点:
- 只有一个出口。(尤其是 N-S 流程图表示特别注意!如下质数判断程序)
- 只有一个入口。判断框有两个出口,但是选择结构(由判断框组成)只有一个出口。
- 结构体内的每一部分都有机会被执行到。对于每个框,都应该有一条从入口到出口的路径通过它。如下左图 A 框就是孤儿。
- 结构体内不存在“死循环”。如下图右侧就是一个“环”

派生结构:
只要符合上述 4 个特点就可以创造出新的结构,也就是基本结构中派生(或组合)出的新结构而已。如下左图,根据需要添加执行框;如下右图,创建多分枝结构(类似 switch-case 结构,N-S其实也有的)。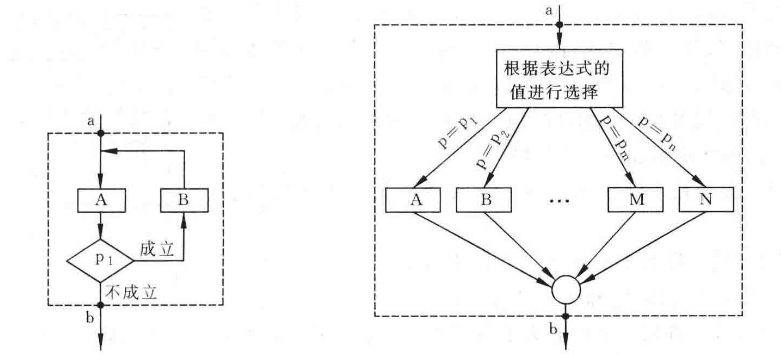
3.5 伪代码表示
流程图和N-S图表示算法直观易懂,但是画起来非常麻烦。算法设计过程中需要反复修改,修改起来非常麻烦(为什么我屈服了,我开始截图了)。
伪代码(pseudo code):用介于自然语言和计算机语言之间的文字和符号来描述算法。特点如下:
- 自上而下书写,每一行表示一个操作
- 不用图形符号,书写方便,格式紧凑,修改方便,容易看懂,便于向计算机语言算法过渡。
- 伪代码写算法并无固定的、严格的语法规则。(我觉得这是最没标准的,但是力求清晰)
优缺点:(C程序P32)
- 伪代码书写格式自由,容易表达出设计者的思想。
- 容易修改,例如加一行或删一行,或将后面某一部分调到前面某个位置,都是很容易做到的。而流程图表示是很不方便处理的。
- 用伪代码很容易写出结构化的算法。
- 不如流程图直观,可能会出现逻辑上的错误(循环体条件和选择条件弄错)
3.6 计算机语言表示
前面所有都是算法的描述(算法的设计是在描述之前),用不同的方法来表示操作的步骤。而要得到真正的结构而不是纸上谈兵就要实现算法。实现算法的方式有拿命算,心算,计算器等。
用计算机解题,就要用计算机实现算法。计算机不认识流程图和伪代码,只有用计算机语言编写的程序才能被计算机执行,因此在使用流程图或伪代码描述一个算法后,还要将它转换为计算机语言程序。
用计算机语言表示算法必须遵循所用的语言的语法规则,这是和伪代码不同地方。
4 简单算法设计
解决问题的一般步骤:(tips:个人添加)
- 抽象建模:对原始问题进行建模,将问题抽象化对待。
- 设计算法:对不同的问题进行不同的算法设计,首先最低要求就是暴力(BF)算法,能进行优化则优化(一般站在巨人肩膀上看问题)。
- 转变思维:使用计算机思维去实现这个算法,即如何用语言来表示你的算法。
- 初始化:一般是很多程序必须考虑的,比如求和
sum=0,求积porduct=1等 - 循环结束条件:往往就是边界问题,是否取得到。
- 尾巴处理问题:有可能最后一步执行后答案没更新导致错误。比如
a123..2.134中提取连续数字,最后一个数字与字符串结束判断问题。
- 初始化:一般是很多程序必须考虑的,比如求和
- 向他人展示你的算法:这部分是加深你对算法的认识,也是对你表达能力的提升。
例 2.1 求阶乘 
- 解题思路:两数相乘后与第三数进行相乘,然后把结果继续与下一个数相乘。一直重复
n-1次。(两两组合) 计算机思维:我们用变量表示两数累乘结果,然后与下一个数进行相乘,以此类推。
关于初始化,第一个数和谁相乘构成两两配对呢?即首先要构建一对出来,那么显然初始化乘积
product=1与1一对最为合适。注意很多算法问题初始化很关键,可以一并处理,类似还有两两求和初始值为sum=0。如果实在不可能找到一个合适的初始值,那么if或者先生成这对。使
product=1, 或者(表示将 1 放入变量
product中)
使
i = 2,或者
使
product = product * i,或者
使
i = i + step,或者(假设这里步长为 1)
如果
,返回
继续向下执行;否则,算法结束。最终
product=5!
:::tips
上述计算机思维特点就是使用循环处理,一两个变量轮替的进行。关键点就是循环的条件设置,通常就在最后一步,到底 i 的值该怎么设置,这与初始值设置有关,总之弄清楚循环经过几次即可。
计算机思维在循环中用的最多,如果不需要中间的运算结果就直接可以用变量交替进行,如果想要那么有两种方式:
- 及时打印出来,但是这种循环结束后还想使用这个数据就不行
- 用数组存起来,下次可以防止重复计算。类似问题就是
- 计算思维方便扩展,即举一反三,比如书上所说只需修改上面的步长
step = 2,问题转换为:::
- 流程图表示:下图左:未输出结果
t;下图右:添加输出框,在流程图结束之前输出结果t
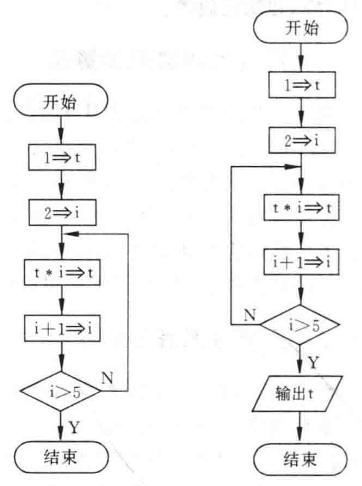
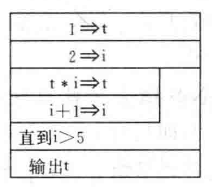
int main() { int i, t; t = 1; i = 2; while (i <= 5) { t = t * i; i = i + 1; } printf(“%d\n”, t); return 0; }
:::successb12@PC:~/chapter2$ gcc -Wall ./src/factorial.c -o ./bin/factorial<br />b12@PC:~/chapter2$ ./bin/factorial<br />b12@PC:~/chapter2$ time ./bin/factorial<br />120<br />real 0m0.007s<br />user 0m0.000s<br />sys 0m0.000s:::- **复杂度分析**:- **时间复杂度**:,循环执行 `n-1` 次。- **空间复杂度**:<a name="rGxCU"></a>### 例 2.2 有 50 个学生,要求输出成绩在 80 分以上学生的学号和成绩- **抽象问题:**为了处理方便,我们需要将两者视为一个整体看,用  表示第 `i` 个学生学号;用 表示第 `i` 个学生成绩。因此问题抽象为以下标 `i` 枚举  逐个查看  是否成立,是就输出学号 ,否则继续看下一个直到看完所有学生,算法结束。(这种就是问题进行转换,用计算思维看待问题,方便使用循环来解决)- **计算思维:**使 `i=1`, 或者 <br /> 如果,则输出 和 。<br /> <br /> 如果,返回到  继续执行,否则算法结束。- **流程图:**左图:不包含输入信息;右图循环输入50名学生信息.| 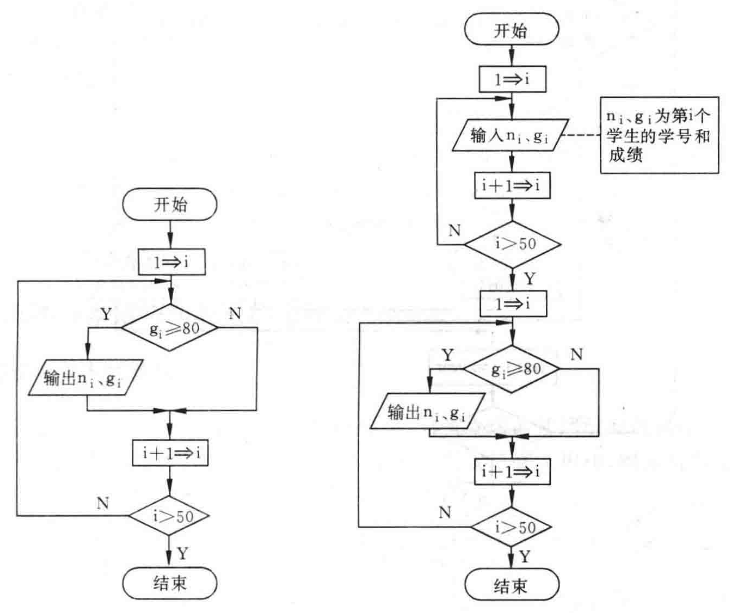 | 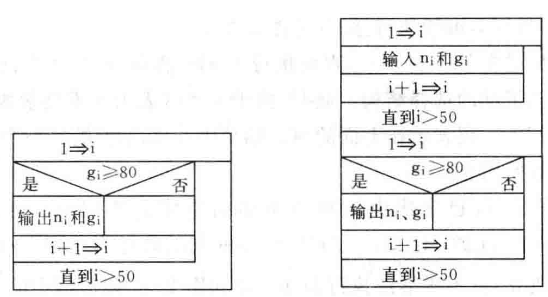 || :---: | :---: |- **伪代码表示**:(这里不处理循环输入信息部分)
begin 1 → i while i ≤ 50 { if g[i] >= 80 then print i, g[i] i + 1 → i } end
- **C语言表示**:(这里处理循环输入,假设 5 名学生,学号随意输入 )```c#include <stdio.h>#define N 5 // 处理5名学生成绩int main() {int id[N]; // 学号数组float score[N]; // 成绩数组,注意是小数// 1.循环输入数据for (int i = 0; i < N; i++) {printf("Input %d student id and score: ", i + 1);scanf("%d%f", &id[i], &score[i]);}// 2.循环查找成绩大于等于80分得学生并输出学号+分数for (int i = 0; i < N; i++) {if (score[i] >= 80) {printf("id:%4d score:%4.1f\n", id[i], score[i]);}}return 0;}
:::success
b12@PC:~/chapter2$ time ./bin/score
Input 1 student id and score: 102 55.5
Input 2 student id and score: 003 88
Input 3 student id and score: 109 65.5
Input 4 student id and score: 55 90.4
Input 5 student id and score: 410 82.5
id: 3 score:88.0
id: 55 score:90.4
id: 410 score:82.5
real 0m35.349s
user 0m0.000s
sys 0m0.000s
:::
复杂度分析:
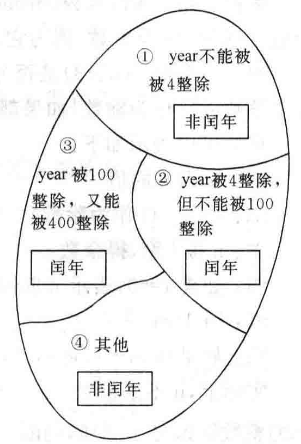
抽象问题:1. 判断闰年 2. 在区间内找到满足条件的闰年
判断闰年的条件:四年一闰,百年不闰,四百年再闰
- 能被 4 整除,但不能被 100 整除的年份都是闰年,如 1600 年、2000 年是闰年。
- 能被 400 整除的年份是闰年。例如 1600年、200年
凡是不能满足以上两个条件都是平年。如 2009 年、2100 年。
|
- 计算思维:设 year 是被检测的年份。
使
year=2000, 或者
若
year 不能被 4 整除,则输出 year 的值和“不是闰年”。然后转到,检查下一个年份
若
year 能被 4 整除,不能被 100 整除,则输出 year 的值和“是闰年”。然后转到
若
year 能被 400 整除,不能被 100 整除,则输出 year 的值和“是闰年”。然后转到
输出
year 的值和“不是闰年”
当
时,转到
继续执行,否则算法结束。 |
 |
| —- | —- |
|
| —- | —- |
流程图:
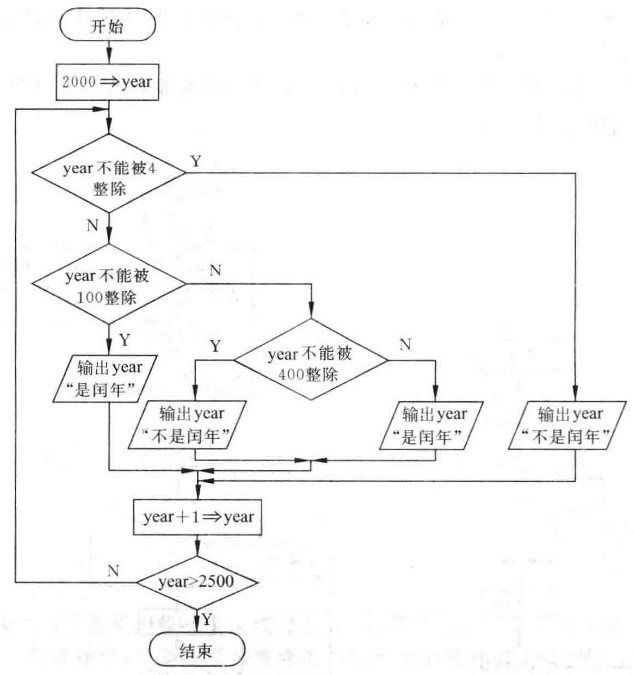 |
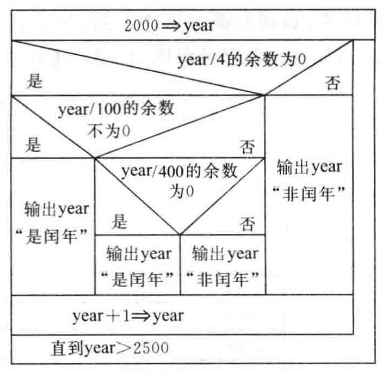 |
|---|---|
伪代码表示:(这里表示的有点牵强)
begin
2000 → year
while year ≤ 2500
{
if year % 4 = 0 then
if year % 100 = 0 then
if year % 400 = 0 then
print year is leap year
else
print year is't leap year
else
print year is leap year
else
print year is't leap year
year + 1 → year
}
end
int main() { for (int year = 2000; year <= 2500; year++) { if (0 == year % 4) { if (0 == year % 100) { if (0 == year % 400) { printf(“%d is leap year\n”, year); } else { printf(“%d is nonleap year\n”, year); } } else { printf(“%d is leap year\n”, year); } } else { printf(“%d is nonleap year\n”, year); } } return 0; }
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/leapyear.c -o ./bin/leapyear<br />b12@PC:~/chapter2$ time ./bin/leapyear<br />b12@PC:~/chapter2$ time ./bin/leapyear<br />2000 is leap year<br />2001 is nonleap year<br />2002 is nonleap year<br />2003 is nonleap year<br />2004 is leap year<br />.................................skip all<br />2496 is leap year<br />2497 is nonleap year<br />2498 is nonleap year<br />2499 is nonleap year<br />2500 is nonleap year
real 0m0.462s<br />user 0m0.000s<br />sys 0m0.016s
:::
- **复杂度分析**:
- **时间复杂度**:,N 是年限区间。
- **空间复杂度**:
<a name="eSm3h"></a>
### 例 2.4 求 
**抽象问题:**找规律,数学归纳法。
1. 第 1 项分子分母可以认为都是 1,即 
1. 第 2 项分子是 1,分母是 2,是前一项分母加一,并且是负数。
1. 第 3 项分子是 1,分母是 3,是前一项分母加一,并且是正数。
因此有分母累加,奇数项符号为负,偶数项符号为正,想办法如何解决符号位即可。1. 负负得正 2.判断奇偶
- **计算思维:**设 `numerator` 表示分子,`denominator` 表示分母, `sign` 表示奇偶项的符号, `term` 表示当前项的值, `sum` 表示累加和。
`numerator=1`<br /> `denominator=2`<br /> `sign=1`<br /> `sign=-1 * sign`<br /> `term=sign*(1/denominator)`<br /> `sum = sum + term`<br /> `denominator=denominator+1`<br /> 若  时,转到  继续执行,否则算法结束。
- **流程图、N-S**表示:
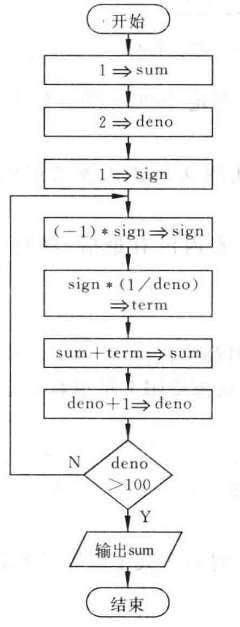
- **伪代码表示**:
begin 1 → sum 2 → denominator 1 → sign while denominator ≤ 2500 { -1 sign → sign sign (1 / denominator) → term sum + term → sum denominator + 1 → denominator } print sum end
- **C语言表示**:
```c
#include <stdio.h>
int main() {
int denominator = 1, sign = 1;
double sum = 0.0, numerator = 1.0, term; // float instead of int
while (denominator <= 100) {
term = sign * numerator / denominator;
sum = sum + term;
denominator = denominator + 1;
sign = -1 * sign;
}
printf("sum:%f\n", sum);
return 0;
}
如果你不是按照浮点数,由于 int / int 只会得到 int ,那么结果就是 1 ,而不是正确答案。
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/polysum.c -o ./bin/polysum
b12@PC:~/chapter2$ time ./bin/polysum
sum:0.688172
real 0m0.008s
user 0m0.000s
sys 0m0.000s
:::
- 复杂度分析:
- 时间复杂度:
,N 是最大分母。
- 空间复杂度:
- 时间复杂度:
例 2.5 给出大于等于 3 的正整数,判断是否是质数
- 解题思路:素数(prime)是指除了 1 和该数本身之外,不能再被其他任何整数整除的数。
计算思维:枚举
,以内所有的除数,是否都存在
成立。
输入
n的值
i=2(i作为除数)
如果
r=0,表示n能够被i整除,输出n不是质数,算法结束;否则执行
如果
,返回
;否则输出
n是质数,算法结束算法优化:
n实际上不需要被都整除,只需要被
的数进行整除判断,甚至只需要被
的数整除即可。即
作为结束条件。证明如下:
- 设
是
的两个因数,如果存在则有
,例如
等,那么由于
可知 a 与 b 成反比,因此当且仅当
时,因最大值为
。因而枚举范围可以优化到
。
- 这也不难理解,为什么可以枚举空间也可以
,这是因为
永远成立。
- 设
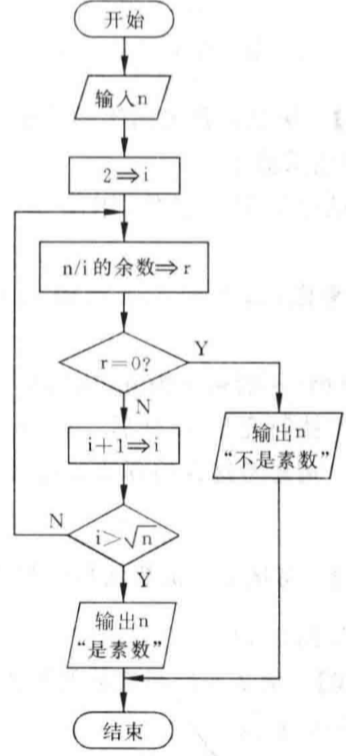
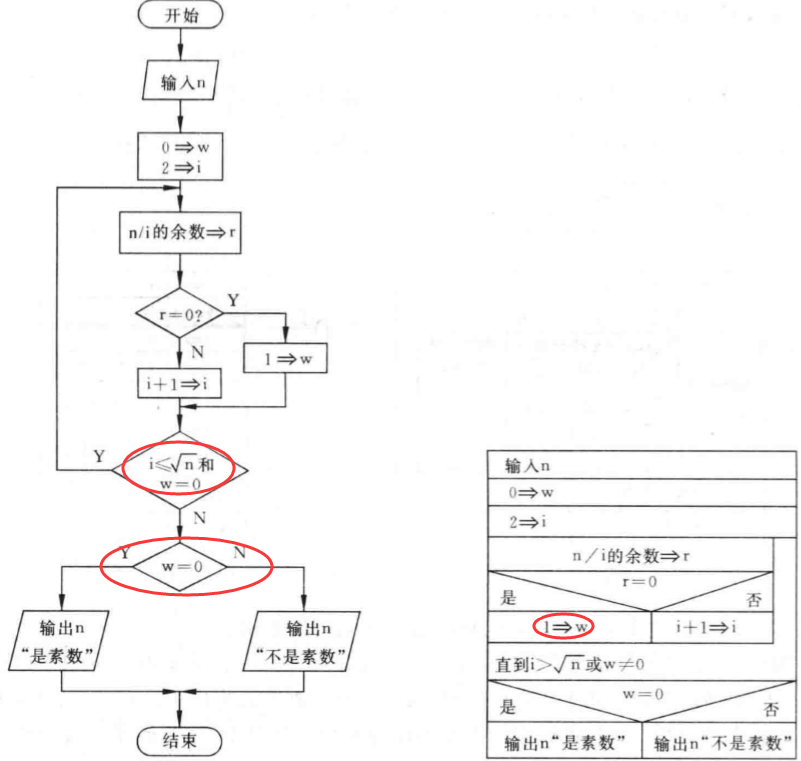
- 流程图:
|
 |
|  |
| :—-: | :—-: |
|
| :—-: | :—-: |
:::tips
流程图(左1)是有两个出口,而标准的结构是要求只有一个出口,否则没法用 N-S 流程图表示(这也是为什么N-S麻烦)。
由于不能分解为三种基本结构,那么就想办法转化。将第一个判断框 r=0? 的两出口点汇合在一起判断,因此使用辅助变量 w 进行标记。
w=1:表示被检查的数为合数。w=0:表示当前还可以继续检查其因子,如果最终任为 0,表示通过所有因子检查,被检查数是质数。
但是代码又可以不这样写,判断条件灵活多样,只要正确都可以。关键一点就是N-S流程图的缺陷。 :::
伪代码表示:(标准的
until型循环)begin input n 2 → i 0 → w n % i → r do if r = 0 then w = 1 else i + 1 → i endif until i <= sqrt(n) and w = 0 if w = 1 then print n isn't prime else print n is prime endif endC语言表示: ```c
include
include
int main() {
int n;
printf(“Please input number:”);
scanf(“%d”, &n);
int i = 2, w = 0;
do {
int remainder = n % i;
if (0 == remainder) {
w = 1;
} else {
i = i + 1;
}
} while (i <= sqrt(n) && 0 == w); // i * i <= n
if (0 == w) {
printf(“%d is prime\n”, n);
} else {
printf(“%d isn’t prime\n”, n);
}
return 0;
}
``
注意下,gcc 编译器没有链接到math库函数,需要加上一个参数-lm即可。
:::danger
b12@PC:~/chapter2$ gcc -Wall ./src/prime.c -o ./bin/prime<br />/usr/bin/ld: /tmp/cc309jbS.o: in functionmain’:
prime.c:(.text+0x81): undefined reference to `sqrt’
collect2: error: ld returned 1 exit status
:::
重新编译下即可:
:::success
b12@PC:~/chapter2$ gcc -Wall ./src/prime.c -o ./bin/prime -lm
b12@PC:~/chapter2$ ./bin/prime
Please input number:13
13 is prime
b12@PC:~/chapter2$ ./bin/prime
Please input number:12
12 isn’t prime
:::
:::tips
这里需要注意下 `while (i <= sqrt(n) && 0 == w); // i i <= n`` 这样写在条件内的求根函数是每次都调用,可以额外用变量保存起来;如果不想调用库函数,那么可以写成 ,不过此举有*溢出风险,建议使用前者的变量替换形式。
:::
5. 结构化程序设计
结构化算法:是由一些基本结构顺序组成的;在基本结构之间不能存在向前向后的跳转,流程的转移至存在于一个基本结构范围内(如循环中流程的跳转)(C程序P31)
一个结构化程序就是用计算机语言表示的结构化算法,用 3 中基本结构组成的程序必然是结构化的程序。这种程序便于编写、阅读、修改和维护,这就减少了程序出错的机会,提高了程序的可能性,保证了程序的质量。
结构化程序设计强调程序设计风格和程序结构的规范化,提倡清晰的结构。把一个复杂问题的求解过程分阶段进行,每个阶段处理的问题都是控制在人们容易理解和处理的范围内。(C语言P34-35,这部分应该不会考,整本书都不涉及开发)
- 自顶向下:整体规划,慢慢具体化。
- 逐步细化
- 模块化设计:“分而治之”思想,把大任务分为若干个子任务,每个子任务用相应的模块去解决。划分模块是应注意模块的独立性,「耦合性」越小越好。
- 结构化编码:将已设计好的算法用计算机语言来表示,即根据一精细化的算法正确地写出计算机程序。(C语言P35)


