- 1、请画出例5.6中给出的3个程序段的流程图
- 和
时,执行循环体的次数">2、请分别统计当
和
时,执行循环体的次数
- 3、输入两个正整数
m和n,求其最大公约数和最小公倍数。 - 4、输入一行字符,分别统计出其中英文字母、空格、数字和其他字符的个数
- 的值,其中 a 是一个数字,n 表示 a 的位数,n由键盘输入,2+22+222+2222+22222(n=5)">5、求
的值,其中 a 是一个数字,n 表示 a 的位数,n由键盘输入,2+22+222+2222+22222(n=5)
- ">6、求阶乘和
- ">7、求公式和
- ">8、输出所有的“水仙花数”。所谓“水仙花数”是指一个3位数,其各位数字立方和等于该数本身。例如,153是一水仙花数,因为
- 9、一个数如果恰好等于它的因子之和,这个数就称为“完数”。例如,6 的因子为 1,2,3,而 6=1+2+3,因此 6 是“完数”。编程序找出1000之内的所有完数,并按下面格式输出其因子: 6 its factors are 1 2 3
- ,求出前 20 项和。">10、有一个分数序列:
,求出前 20 项和。
- 11、一个球从
100m高度自由落下,每次落地后反跳回原高度的一半,再落下,再反弹。求它在第10次落地时,共经过多少米,第10次反弹多高 - 12、猴子吃桃问题。猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。求第1天共摘了多少个桃子。
- 求平方根的迭代公式为
">13、用迭代法求
求平方根的迭代公式为
- 14、用牛顿迭代法求下面方程在 1.5 附近的根:
- 15、用二分法求下面方程在(-10,10)之间的根:
- 16、输出菱形
- 17、两个乒乓球队进行比赛,各出
3人。甲队为A,B,C,乙队为X,Y,Z。已抽签决定比赛名单。有人向队员打听比赛的名单,A说他不和X比,C说他不和X,Z比,请编程序找出 3 对赛手的名单。
1、请画出例5.6中给出的3个程序段的流程图
解题思路:主要考察 break , continue 的使用判断。
// 程序1:完全输出#include <stdio.h>int main () {int n = 0;for (int i = 1; i <= 4; i++) {for (int j = 1; j <= 5; j++, n++) {if (0 == n % 5) { // 5个数一换行printf("\n");}printf("%d\t", i * j);}}printf("\n");return 0;}// 程序2:除了第三行,其它都输出#include <stdio.h>int main () {int n = 0;for (int i = 1; i <= 4; i++) {// if (3 == i) continue;for (int j = 1; j <= 5; j++, n++) {if (0 == n % 5) { // 5个数一换行printf("\n");}if (3 == i && 1 == j) {break; // 不打印第三行,等价上面continue}printf("%d\t", i * j);}}printf("\n");return 0;}// 程序3:除了第三行第一列不输出(第三行其他列输出),其它都输出#include <stdio.h>int main () {int n = 1; // 让首行不空for (int i = 1; i <= 4; i++) {for (int j = 1; j <= 5; j++, n++) {if (0 == n % 5) { // 5个数一换行printf("\n");}if (3 == i && 1 == j) {continue; // 不打印第三行第一列}printf("%d\t", i * j);}}printf("\n");return 0;}
流程图:
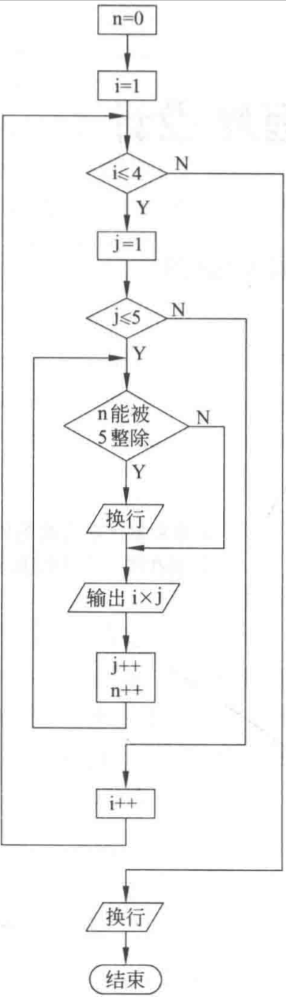 |
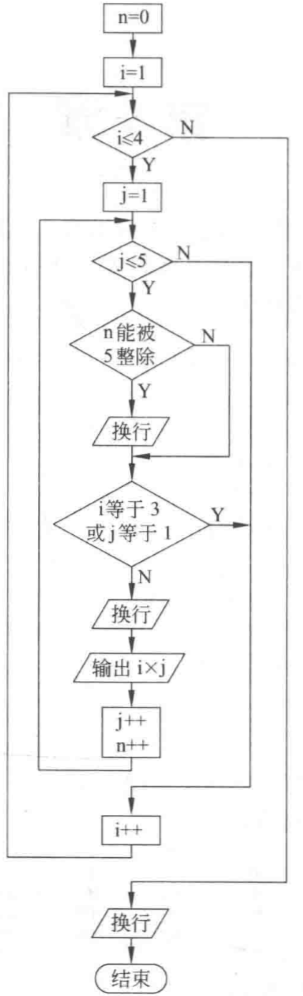 |
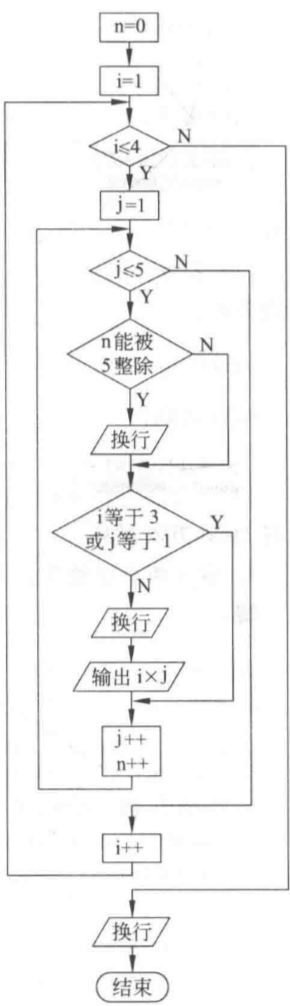 |
|---|---|---|
分别编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/matrix1.c -o ./bin/matrix1
b12@PC:~/chapter5$ ./bin/matrix1 # 第一行空白是因为 n = 0
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
b12@PC:~/chapter5$ gcc -Wall ./src/matrix2.c -o ./bin/matrix2
b12@PC:~/chapter5$ ./bin/matrix2 # 第一行空白是因为 n = 0
1 2 3 4 5
2 4 6 8 10
4 8 12 16 20
b12@PC:~/chapter5$ gcc -Wall ./src/matrix3.c -o ./bin/matrix3
b12@PC:~/chapter5$ ./bin/matrix3
1 2 3 4
5 2 4 6 8
10 6 9 12
15 4 8 12 16
20
:::
2、请分别统计当  和
和  时,执行循环体的次数
时,执行循环体的次数
解题思路:公式求
的近似值,直到发现某一项
t 的绝对值小于为止。本题就是在统计
while 循环共执行多少次,使用一个 count = 0 变量进行统计即可。
代码也可以使用define epsilon 1e-6 分别进行计算,下面只是 IO
#include <stdio.h>#include <math.h> // fabs 函数int main () {double epsilon, pi = 0.0, denominator = 1.0, item = 1.0;printf("Please input the epsilon: ");scanf("%lf", &epsilon); // double 输入要 %lfint sign = 1, count = 0; // 符号,计数器while (fabs(item) >= epsilon) {pi += item; // 注意先加还是后加?denominator += 2;sign *= -1;item = sign / denominator;count++;}pi *= 4;printf("PI:%10.8f\n", pi);printf("count:%d\n", count);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/calPi.c -o ./bin/calPi
b12@PC:~/chapte./bin/calPi
Please input the epsilon: 1e-6
PI:3.14159065
count:500000
b12@PC:~/chapter5$ ./bin/calPi
Please input the epsilon: 1e-8
PI:3.14159263
count:50000000
:::
3、输入两个正整数m和n,求其最大公约数和最小公倍数。
解题思路:求 gcd(a, b) 是非常常见的问题,书中没有给出辗转相除法(欧几里得算法)的证明,但是我们可以使用暴力算法进行破解,两数最大公因数就是两数因子交集部分最大的那个数。而最小公倍数就是两数乘积除去最大公因数(数学问题,分母通分问题等)
代码1:暴力枚举
#include <stdio.h>int main () {int m, n;printf("Please input two digits: ");scanf("%d %d", &m, &n);// 暴力枚举任一数的因子的同时判断是否是另一个数因子int gcd = 1; // 最小就是 1for (int i = 2; i < m; i++) {if (0 == m % i && 0 == n % i) { // 两者因子交集元素gcd = i; // 逐渐更新为最大公因数}}printf("gcd(%d, %d):%d\n", m, n, gcd);printf("lcm(%d, %d):%d\n", m, n, m * n / gcd); // 有溢出风险return 0;}
辗转相除法:
 |
|
|---|---|
代码2:
更相减损术
#include <stdio.h>int main () {int m, n;printf("Please input two digits: ");scanf("%d %d", &m, &n);// 更相减损术:1.可半者半之int gcd = 1, a = m, b = n; // 半的乘积while (0 == a % 2 && 0 == n % 2) {gcd *= 2;a /= 2;b /= 2;}// 2.不可半者,副置分母、子之数,以少减多,更相减损,求其等也while (a != b) {if (a > b) {a -= b;} else {b -= a;}}gcd *= a;printf("gcd(%d, %d):%d\n", m, n, gcd);printf("lcm(%d, %d):%d\n", m, n, m * n / gcd); // 有溢出风险return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/gcdLcm.c -o ./bin/gcdLcm
b12@PC:~/chapter5$ ./bin/gcdLcm
Please input two digits: 35 49
gcd(35, 49):7
lcm(35, 49):245
:::
4、输入一行字符,分别统计出其中英文字母、空格、数字和其他字符的个数
解题思路:由于没有学习数组,但是本例也可以直接使用 gerchar() 从终端进行读取单个字符,只需要判断当前读入字符是否是 \n 就结束(这就意味着如果字符中出现换行是不行的!解决办法有点麻烦)
#include <stdio.h>int main () {int letters = 0, space = 0, digits = 0, other = 0;printf("Please input oneline string: ");char ch = getchar();while ('\n' != ch) {if (('A' <= ch && ch <= 'Z') || ('a' <= ch && ch <= 'z')) {letters++;} else if ('0' <= ch && ch <= '9') {digits++;} else if (' ' == ch) {space++;} else {other++;}ch = getchar(); // 再次输入}printf("letters:%d, digits:%d, space:%d, other:%d\n",letters, digits, space, other);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/countChar.c -o ./bin/countChar
b12@PC:~/chapter5$ ./bin/countChar
Please input oneline string: C language is shit!
letters:15, digits:0, space:3, other:1
:::
5、求  的值,其中 a 是一个数字,n 表示 a 的位数,n由键盘输入,2+22+222+2222+22222(n=5)
的值,其中 a 是一个数字,n 表示 a 的位数,n由键盘输入,2+22+222+2222+22222(n=5)
解题思路:对于任意 其规律是
,但是由于
,因此通项公式就是
但是需要注意的就是第 0 项应该如何处理,这是小细节,虽然题目没说出,但是默认其就是 0 ,即只能从第一项开始。
#include <stdio.h>int main () {int a, n;printf("Please input a and n (eg: 2 5): ");scanf("%d %d", &a, &n);double sum = 0, item = 0; // 注意初始化for (int i = 1; i <= n; i++) {item = item * 10 + a; // 上一项的只保留在item中sum += item; // 前后相加顺序?}printf("sum:%.0f\n", sum);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/seqSum.c -o ./bin/seqSum
b12@PC:~/chapter5$ ./bin/seqSum
Please input a and n (eg: 2 5): 2 5
sum:24690
b12@PC:~/chapter5$ ./bin/seqSum
Please input a and n (eg: 2 5): 11 3 # 尝试两位数?
sum:1353
:::
从上面输入两位数开始看到,居然不行了?因为 啊!为什么出现这种情况,因为位权×10,而不是×100,因为是两位数,其该“左移两位”然后再加上新的
11 才是该项结果。
因此对于输入任意数字而不是只有个位数,只需要计算该数字长度就可知道前一个数字“左移多少位”。
#include <stdio.h>#include <math.h>int main () {int a, n;printf("Please input a and n (eg: 2 5): ");scanf("%d %d", &a, &n);if (0 == a || 0 == n) { // 判断原因就是 log10(a) 要求真数大于0printf("sum:0\n");return -1; // 异常}int bitpower = (int)pow(10, (int)log10(a) + 1); // 1:10,11:100double sum = 0, item = 0; // double 防止溢出for (int i = 1; i <= n; i++) {item = item * bitpower + a; // 上一项的只保留在item中printf("item:%f\n", item);sum += item;}printf("sum:%.0f\n", sum);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/seqSum.c -o ./bin/seqSum -lm
b12@PC:~/chapter5$ ./bin/seqSum
Please input a and n (eg: 2 5): 11 6
item:11.000000
item:1111.000000
item:111111.000000
item:11111111.000000
item:1111111111.000000
item:111111111111.000000
sum:112233445566 # 早就超过int范围
:::
6、求阶乘和 
解题思路:通项公式已给出,,而相邻两项之间有特殊关系
。下面分别尝试暴力法和使用相邻两项迭代方式验证程序。
#include <stdio.h>double factorial(int a) {double fact = 1; // 0!,或大数int溢出for (int i = 2; i <= a; i++) {fact *= i;}return fact;}int main () {int n;printf("Please input n: ");scanf("%d", &n);double sum = 0; // 注意可能溢出if (0 == n) {printf("sum:%22.15e\n", sum);return 0;}for (int i = 1; i <= n; i++) { // 从第一项开始sum += factorial(i);}// 优化,使用前一项值// double sum = 0, item = 1; // double 防止溢出// for (int i = 1; i <= n; i++) {// item = item * i; // 上一项的值保留在item中// sum += item;// }printf("sum:%22.15e\n", sum);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/factorialSum.c -o ./bin/factorialSum
b12@PC:~/chapter5$ ./bin/factorialSum
Please input n: 20
sum: 2.561327494111820e+18
b12@PC:~/chapter5$ ./bin/factorialSum
Please input n: 0
sum: 0.000000000000000e+00
:::
7、求公式和 
解题思路:没有规律,三次 for 暴力求解。
:::tips
请不要在一层 for 里面使用 if 判断,这样开销还不如三次 for 小。
:::
#include <stdio.#include <stdio.h>#define N1 100#define N2 50#define N3 10int main () {double sum = 0;for (int i = 1; i <= N1; i++) {sum += i;}for (int i = 1; i <= N2; i++) {sum += i * i; // double防止溢出}for (int i = 1; i <= N3; i++) {sum += 1 / i; // 实数除法而不是整数除数}printf("sum:%15.6f\n", sum);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/getSum.c -o ./bin/getSum
b12@PC:~/chapter5$ ./bin/getSum
sum: 47976.000000 # 输出与机器有关,精度问题
:::
8、输出所有的“水仙花数”。所谓“水仙花数”是指一个3位数,其各位数字立方和等于该数本身。例如,153是一水仙花数,因为 
解题思路:首先三位数分别拆分,然后进行 n 次幂计算得到和即可。如下程序是对原来答案的扩展,可以接受人任意位数,并在区间 进行枚举。
#include <stdio.h>#include <math.h>int main () {int n;printf("Please input a number: ");scanf("%d", &n);// 1.开始进行验证for (int start = pow(10, n - 1), end = pow(10, n); start < end; start++) {int x = start, sum = 0;do {int remainder = x % 10, product = 1;for (int i = 0; i < n; i++) {product *= remainder;}sum += product;x /= 10;} while (0 != x);if (sum == start) {printf("%d ", start);}}printf("\n");return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/Daffodils.c -o ./bin/Daffodils -lm
b12@PC:~/chapter5$ ./bin/Daffodils
Please input a number: 3
153 370 371 407
b12@PC:~/chapter5$ ./bin/Daffodils
Please input a number: 4
1634 8208 9474
b12@PC:~/chapter5$ ./bin/Daffodils
Please input a number: 5
54748 92727 93084
:::
9、一个数如果恰好等于它的因子之和,这个数就称为“完数”。例如,6 的因子为 1,2,3,而 6=1+2+3,因此 6 是“完数”。编程序找出1000之内的所有完数,并按下面格式输出其因子: 6 its factors are 1 2 3
解题思路:一个数因子就是可以这个数能被其因子整除。因此最简单的方式就是暴力枚举所有的因子,然后累加和是否等于 n 即可,所有的过程可以使用递归实现,但是其结果就是与上述要求相反,因为递归在退栈的时候进行打印(本质就是两次枚举)。
#include <stdio.h>int factorSum(int factor, int n, int sum) {// factor从小到大枚举到n,并累加到sumif (sum > n) { // 当因子和大于n肯定不是完数return 0;} else if (factor == n) { // 当枚举到自身即是递归终止判断if (n == sum) { // 根据因子和是否等于n判断返回printf("%d its factors are ", n);return 1;} else {return 0;}} else if (0 == n % factor) { // 对于当前是n的因子,需要根据最后结果判断进行打印if (factorSum(factor + 1, n, sum + factor)) {printf("%d ", factor);return 1;}} else { // 否则当前不是n的因子,继续加大factor进行枚举,一定要将最后的状态返回return factorSum(factor + 1, n, sum);}return 0;}int main () {int n;printf("Please input a number(2->1000): ");scanf("%d", &n);for (int i = 2; i <= n; i++) {if (factorSum(1, i, 0)) {printf("\n");}}return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/perfectNum.c -o ./bin/perfectNum
b12@PC:~/chapter5$ ./bin/perfectNum
Please input a number(1->1000): 1000
6 its factors are 3 2 1
28 its factors are 14 7 4 2 1
496 its factors are 248 124 62 31 16 8 4 2 1
:::
至于书本上第一个使用 switch-case 和如何获知 1000 范围内怎么就有 10 个因子的变量,其实就是他自己亲自试出来的,相比之下,其使用 for 循环暴力枚举过程更加清晰易懂。
#include <stdio.h>int main () {int n;printf("Please input a number(2->1000): ");scanf("%d", &n);for (int i = 2; i <= n; i++) { // 1.枚举2->n以内的数int sum = 0;for (int j = 1; j < i && sum <= i; j++) { // 当因子大于i可以终止if (0 == i % j) {sum += j;}}if (sum == i) {printf("%d, its factors are ", i);for (int j = 1; j < i; j++) {if (0 == i % j) {printf("%d ", j);}}printf("\n");}}return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/perfectNum.c -o ./bin/perfectNum
b12@PC:~/chapter5$ ./bin/perfectNum
Please input a number(2->1000): 600
6, its factors are 1 2 3
28, its factors are 1 2 4 7 14
496, its factors are 1 2 4 8 16 31 62 124 248
:::
10、有一个分数序列: ,求出前 20 项和。
,求出前 20 项和。
解题思路:照题意可以发规律,第 n+1 项的分子是第 n 项分子分母之和,第 n+1 项的分母是第 n 项分子,因此照着写出程序即可。
#include <stdio.h>int main () {int n;printf("Please input a number: ");scanf("%d", &n);double numerator = 1, denominator = 2, sum = 0, tmp;for (int i = 1; i <= n; i++) {sum += denominator /numerator; // 为什么在这个位置?而不是在最后?与初始化有关tmp = numerator; // 先保存前一项(n-1)的分子numerator = numerator + denominator; // 更新第n项分子denominator = tmp; // 更新第n项分母}printf("sum = %16.10f\n", sum);return 0;}
编译运行:(因为浮点数原因,与书本结果有误差很正常)
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/seqSum.c -o ./bin/seqSum
b12@PC:~/chapter5$ ./bin/seqSum
Please input a number: 20
sum = 32.4386015793
b12@PC:~/chapter5$ ./bin/seqSum
Please input a number: 100
sum = 161.8813206723
:::
11、一个球从 100m 高度自由落下,每次落地后反跳回原高度的一半,再落下,再反弹。求它在第10次落地时,共经过多少米,第10次反弹多高
解题思路:明确初始状态和每次落地经过的路程问题是理顺整个循环的关键。往往整个循环不在于难,而在于初始和结束状态的细节问题上。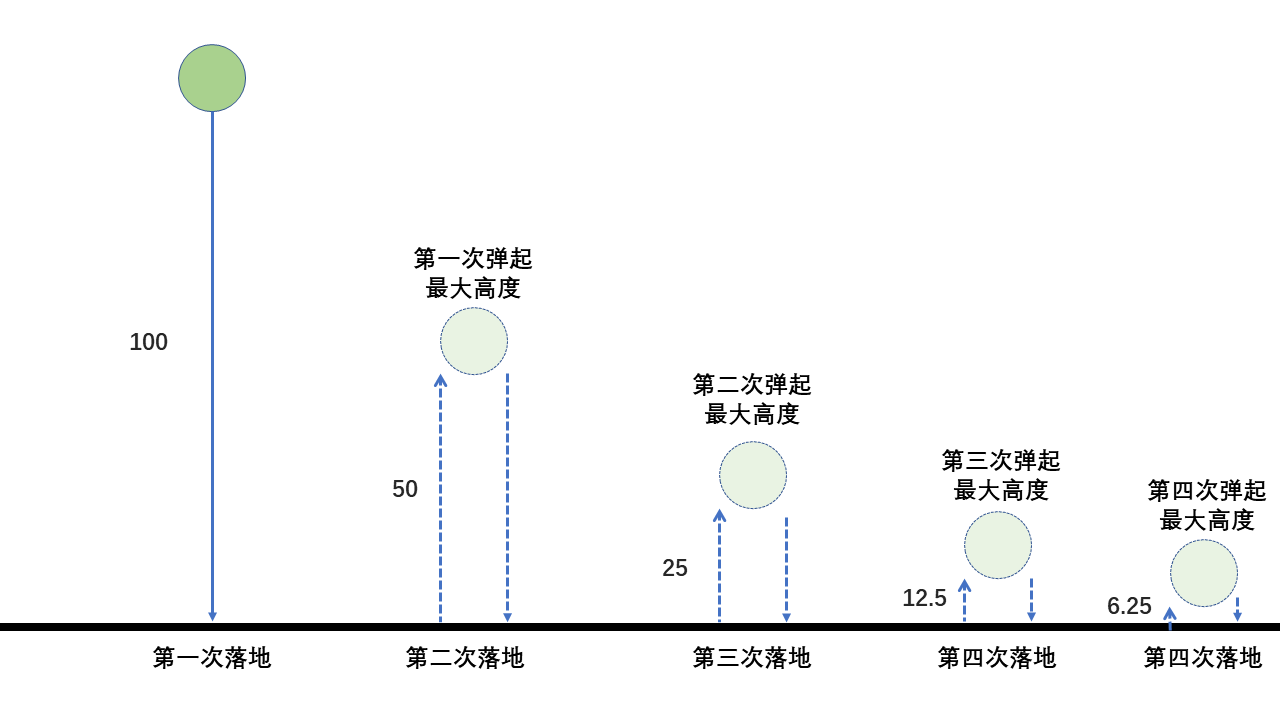
如上图所示,初始状态就是高度 h = 100 ,路程因为还没掉落所以是 s = 0 ,当第一次掉落后每个状态对应的就是上下两个过程(路程是两倍的高度,落地次数比弹起高度多一次),即是说后面的都是重复过程,唯独第一次下落比较特殊。
#include <stdio.h>#define Height 100int main () {int n;printf("Please input a number: ");scanf("%d", &n);double sn = Height, hn = Height / 2; // hn已经是第二次开始状态for (int i = 2; i <= n; i++) {sn += 2 * hn;hn /= 2;}printf("S%d = %fm\n", n, sn);printf("%d bounce %fm\n", n, hn);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/bounce.c -o ./bin/bounce
b12@PC:~/chapter5$ ./bin/bounce
Please input a number: 10
S10 = 299.609375m
10 bounce 0.097656m
b12@PC:~/chapter5$ ./bin/bounce
Please input a number: 4
S4 = 275.000000m
4 bounce 6.250000m
:::
12、猴子吃桃问题。猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。求第1天共摘了多少个桃子。
解题思路:同上题解题思路,本题是倒推过程,给你末状态让你推出初始状态。需要注意的就是第 n 天吃之前的桃子数是第 n-1 天吃了后剩下的。不妨设猴子中午吃桃子,那么最后一天上午之前的桃子就是前一天下午留的。最重要的是题目所说的终状态是 f(9) = 1 即第 9 天没有吃,只剩下一个,让求第一天早上(在它吃刚摘桃子之前的个数,而不是第一题它吃完剩下的个数)共摘了多少个。(很多人会多算一倍)
即有如下公式:
然后现在给定状态为第 10 天早上剩下 1 个,即是第 9 天晚上剩余 1 状态。根据上述公式设第 n-1 天早上共有 x 个,则有方程为 ,如此得到第
n-1 天早上有,如此递推即可得到第
1 天早上剩余多少个。这也是为何程序执行 9 次而不是 10 次。
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | 第八天 | 第九天 | 第十天 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 早上 | 1534 | 766 | 382 | 190 | 94 | 46 | 22 | 10 | 4 | 1 |
| 开吃 | 768 | 384 | 192 | 96 | 48 | 24 | 12 | 6 | 3 | |
| 晚上 | 766 | 382 | 190 | 94 | 46 | 22 | 10 | 4 | 1 |
对原文的题目进行拓展,设输入第 n 天,剩余 k 个,求第一天(早上)共摘了多少个。
#include <stdio.h>int main () {int n, k;printf("Please input day, rest peaches: ");scanf("%d %d", &n ,&k);if (0 >= k || 0 >= n || 0 == k % 2) {printf("Invalid input\n");return -1;}int morning, night = k;while (n > 1) { // 循环执行 n-1 次原因?morning = 2 * (night + 1); // 今天早上printf("Day %d ate %d peaches\n", n - 1, morning / 2 + 1);night = morning; // 前一天晚上(为什么?)n--;}printf("First day : %d\n", morning);return 0;}
编译运行:(不要太大数字,会导致整型溢出;且 k 必定为奇数)
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/peaches.c -o ./bin/peaches
b12@PC:~/chapter5$ ./bin/peaches
Please input day, rest peaches: 10 1
Day 9 ate 3 peaches
Day 8 ate 6 peaches
Day 7 ate 12 peaches
Day 6 ate 24 peaches
Day 5 ate 48 peaches
Day 4 ate 96 peaches
Day 3 ate 192 peaches
Day 2 ate 384 peaches
Day 1 ate 768 peaches
First day : 1534
b12@PC:~/chapter5$ ./bin/peaches
Please input day, rest peaches: 15 3
Day 14 ate 5 peaches
Day 13 ate 10 peaches
Day 12 ate 20 peaches
Day 11 ate 40 peaches
Day 10 ate 80 peaches
Day 9 ate 160 peaches
Day 8 ate 320 peaches
Day 7 ate 640 peaches
Day 6 ate 1280 peaches
Day 5 ate 2560 peaches
Day 4 ate 5120 peaches
Day 3 ate 10240 peaches
Day 2 ate 20480 peaches
Day 1 ate 40960 peaches
First day : 81918
:::
13、用迭代法求  求平方根的迭代公式为
求平方根的迭代公式为 
69.x的平方根(简单)
上图有个公式 就是泰勒级数的简化,其定义为:如果在点
具有任意阶导数,则幂级数
称为在点 处的泰勒级数。(为什么可以拿来求根?我菜不知道)
14、用牛顿迭代法求下面方程在 1.5 附近的根:
解题思路:本题就是上一题一样,无非就是前者泰勒级数的一阶导数 而已。即有
成立。令
,求得其切线与
x 轴交点即
- 设方程的第一个迭代点
,不断进行迭代获得
,直到两点之间距离小于
即可得到答案。
- 关键是现在如何求出
呢?求导脑子算很容易,但是计算机恐怕难了,如何给它一个方程让它自动给我们求出导数呢?(提示:多项式的表达方式以及用链表实现求导)。但是本题很简单的方程,我们可以直接写出导数
,也就是硬编码,只对当前这个方程管用,其它不管。
- 关于书中出现
是怎么来的?为什么可以这样?原因是减少多项式乘法次数,简单说就是「秦九算法」,也可以不需要这样算,直接用 pow(x, n) 或者暴力循环求 x 的幂计算。同样该乘法也只针对本函数进行处理,也是硬编码。
#include <stdio.h>#include <math.h>#define EPS 1e-5int main () {// x0表示前一个与x轴交点,x1后一个与x轴交点,fx表示f(x),f1表示f'(x)double x0 = 1.5, x1, fx, f1;while (1) { // 注意为什么要参考答案用do-while,区别在哪里?fx = ((2 * x0 - 4) * x0 + 3) * x0 - 6;f1 = (6 * x0 - 8) * x0 + 3;x1 = x0 - fx / f1;if (fabs(x0 - x1) < EPS) break;x0 = x1; // 记录x1}printf("The root of equation is %5.2f\n", x1);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/root.c -o ./bin/root -lm
b12@PC:~/chapter5$ ./bin/root
The root of equation is 2.00
:::
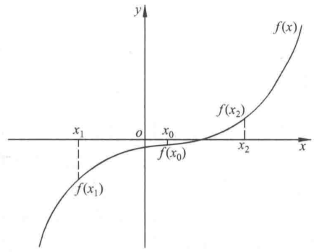
15、用二分法求下面方程在(-10,10)之间的根:
零点定理:如果函数
在区间
上的图象是连续不断的一条曲线,并且有
,那么函数
在区间
内有零点,即至少存在一个
使得
,这个
c也就是方程的根。
1. 函数图像如图,可知其是单调递增的,证明: a = 6 > 0 可知 1. 由零点定理,只需要判断区间端点是否异号得知区间是否有效,题目给定区间 1. 判断输入区间内是否存在零点 4 1. 设 1. 当 1. 当 |
 |
|---|---|
N-S流程图:
#include <stdio.h>#include <math.h>#define EPS 1e-5int main () {// 1.区间端点值检测,为什么用do-while?double x1, x2, x0, fx1, fx2, fx0;do {printf("Please input x1 & x2:");scanf("%lf %lf", &x1, &x2);fx1 = ((2 * x1 - 4) * x1 + 3) * x1 - 6;fx2 = ((2 * x2 - 4) * x2 + 3) * x2 - 6;} while (fabs(fx1 * fx2 > 0));// 2.二分收缩区间,因为一定存在f(x1)*f(x2)>0可知目标区间while (fabs(x1 - x2) >= EPS) { // 注意与书本f(x0)<EPS?x0 = (x2 + x1) / 2; // double 不考虑溢出fx0 = ((2 * x0 - 4) * x0 + 3) * x0 - 6;if (fx0 * fx1 < 0) { // 证明零点在[x1,x0]x2 = x0;fx2 = fx0;} else { // 证明零点在[x0,x2]x1 = x0;fx1 = fx0;}}printf("x = %6.2f\n", x0);return 0;}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/bisectRoot.c -o ./bin/bisectRoot -lm
b12@PC:~/chapter5$ ./bin/bisectRoot
Please input x1 & x2:-10 1.5
Please input x1 & x2:-10 10
x = 2.00
:::
16、输出菱形
PTA编程—循环2
上面是综合成一循环处理,使用的就是中心对称思想,但是书本上给出分为两部分处理,上面 4 行,下面 3 行单独输出。(教材上答案是相邻星星是没有空格的,并且很多关系不清楚,从 0 开始数很容易让人迷惑)
#include <stdio.h>int main () {// 1.共4行for (int row = 0; row < 4; row++) {// 2.3-row前置空格for (int i = 0; i < 4 - 1 - row; i++) {printf(" ");}// 3.2 * row + 1 个星星 == [0,2*row]for (int j = 0; j < 2 * row + 1; j++) {printf("*");}// 4.每行换行printf("\n");}// 5.后打印 3 行for (int row = 0; row < 3; row++) {// 6.row+1前置空格for (int i = 0; i < 1 + row; i++) {printf(" ");}// 7.5 - 2 * row 个星星 == [0,2*row]for (int j = 0; j < 5 - 2 * row; j++) {printf("*");}// 8.每行换行printf("\n");}}
编译运行:
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/asterisk.c -o ./bin/asterisk
b12@PC:~/chapter5$ ./bin/asterisk
**
*
*
*
**
:::
17、两个乒乓球队进行比赛,各出3人。甲队为A,B,C,乙队为X,Y,Z。已抽签决定比赛名单。有人向队员打听比赛的名单,A说他不和X比,C说他不和X,Z比,请编程序找出 3 对赛手的名单。
解题思路:逻辑推理题
- X 既不与 A 比赛,又不与 C 比赛,必然与 B 比赛。
- C 既不与 X 比赛,又不与 Z 比赛,必然与 Y 比赛。
- 剩下的只能是 A 与 Z 比赛
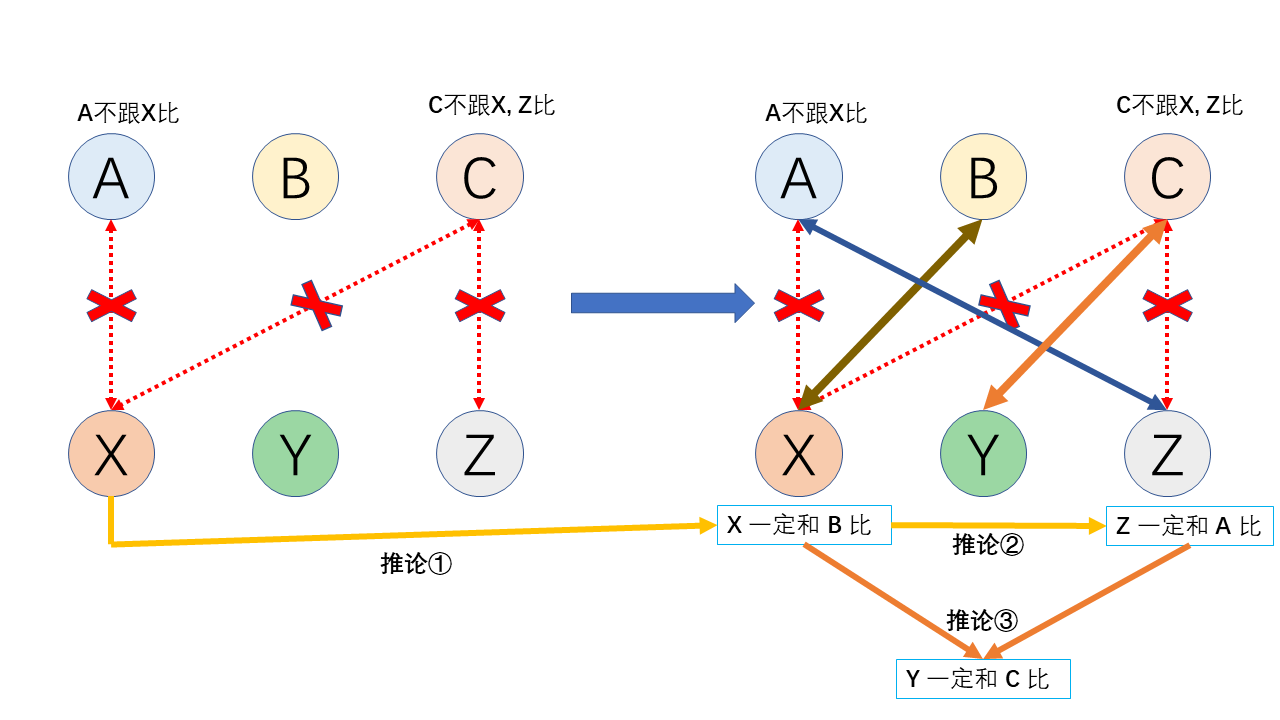
使用计算机思维就是枚举:根据排列共有 种可能,对应下图右侧
6 个枚举可能,最后只要验证即可。
| A对X枚举:后面全错 |  |
|---|---|
| A对Y枚举: - B对X,则C对Z(错误) - B对Z,则C对X(错误) |
 |
| A对Z枚举: - B对X,则C对Y(成功) - B对Y,则C对X(错误) |
 |
但是我们怎么模拟这个过程,找到一种组合就开始验证是否成立,否则就错误。被选择
回溯法:暴力枚举所有状态,不行就撤销,也就是当前选择的状态会影响到之后的选择的时候就用回溯法。 与用
for或者while枚举最大区别就是需要知道之前从哪里来要回哪里去,即必须存储之前的选择,而函数递归就是栈实现的。
#include <stdio.h>char team1[3] = {'A', 'B', 'C'}; // 甲队共三人,用字符表示char team2[3] = {'X', 'Y', 'Z'}; // 乙队共三人,用字符表示int team2PalyerisChosen[3] = {0, 0, 0}; // 标志乙队对手是否被选,默认没选// 记录两队比赛信息,甲队第 i 个对手 VS 乙队第 matchInfo[i] 个对手int matchInfo[3] = {-1, -1, -1}; // -1 只是初始化表示都没选择void backtrace(int p) {/* 回溯函数:枚举甲队第 team1[p] 队员对战乙队队员的所有可能 */// 1.递归终止条件,p == 3if (3 == p) {// 此 if 语句就是上面逻辑判断,如果匹配信息合法,那么就打印比赛信息if (matchInfo[0] != 0 && matchInfo[2] != 0 && matchInfo[2] != 2) {printf("%c VS %c\n", team1[0], team2[matchInfo[0]]);printf("%c VS %c\n", team1[1], team2[matchInfo[1]]);printf("%c VS %c\n", team1[2], team2[matchInfo[2]]);}return;}// 2.回溯枚举:甲队第 p 个队员可能与乙队 X,Y,Z 都 PKfor (int i = 0; i < 3; i++) {// team1[p] 和 乙队第 i 个队员 pk 前提是 乙队第 i 个队员还没和别人配对if (!team2PalyerisChosen[i]) {// 选择状态:乙队第 i 个队员被选中; 记录 甲队第 p 个选手 VS 乙队第 i 个对手team2PalyerisChosen[i] = 1;matchInfo[p] = i;backtrace(p + 1); // 开始甲队下一个队员匹配情况// 撤销状态:甲队第 p 个选手 VS 乙队第 i 个选手 导致之后比赛不合法team2PalyerisChosen[i] = 0; // 表示乙队第 i 个选手尚未匹配matchInfo[p] = -1; // 表示甲队第 p 个选手比赛信息尚未确定}}}int main () {backtrace(0);return 0;}
但是其实可以直接写成书本上的 for 嵌套枚举,这样更容易理解,但是上述「回溯法」是理解递归之必须的,且是最常用的暴力枚举法,也是动态规划的前奏。实在不清楚可以看下面状态的清理过程。
乒乓球比赛.pptx
#include <stdio.h>int main () {for (int A = 'X'; A <= 'Z'; A++) {if ('X' == A) continue; // 剪枝1:A<->Xfor (int B = 'X'; B <= 'Z'; B++) {if (B == A) continue; // 剪枝:一对一for (int C = 'X'; C <= 'Z'; C++) {if (C == B || C == A) continue; // 剪枝:一对一if ('X' != C && 'Z' != C) { // 剪枝2:C<->X,C<->Zprintf("A vs %c\nB vs %c\nC vs %c\n", A, B, C);}}}}return 0;}
编译运行:(注意:以上 continue 都可以使用 if 替换为相反条件)
:::success
b12@PC:~/chapter5$ gcc -Wall ./src/pingpangTest.c -o ./bin/pingpangTest
b12@PC:~/chapter5$ ./bin/pingpangTest
A vs Z
B vs X
C vs Y
:::

