问题

给定三角形 3 个点的坐标，在给定一个点 (x, y) ，判断该点是否在三角形中。

解法

面积比较

判断 的面积与 是否相等。若相等则 O 在内部，反之则在外部。

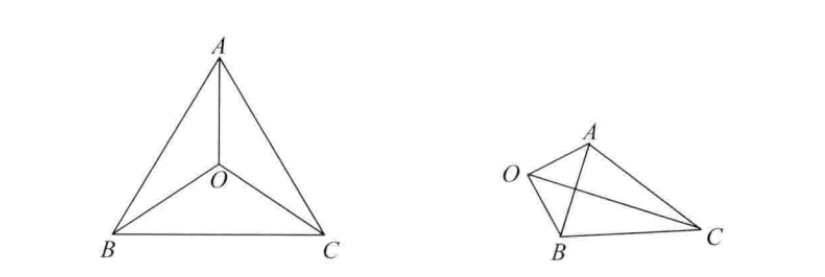
如何求三角形的面积？

海伦公式：

interface IPointer {
  x: number;
  y: number;
}
var pointInTriangle = function (
o: IPointer,
 a: IPointer,
 b: IPointer,
 c: IPointer
): boolean {
  var ab = getDistance(a, b),
      bc = getDistance(b, c),
      ac = getDistance(a, c),
      ao = getDistance(a, o),
      bo = getDistance(b, o),
      co = getDistance(c, o),
      area = getTriangleArea(ab, bc, ac),
      area1 = getTriangleArea(ab, ao, bo),
      area2 = getTriangleArea(ac, ao, co),
      area3 = getTriangleArea(bc, bo, co);
  // 两点距离 == 直线长度
  function getDistance(p1: IPointer, p2: IPointer) {
    var x1 = p1.x,
        x2 = p2.x,
        y1 = p1.y,
        y2 = p2.y,
        result;
    result = Math.abs(Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2)));
    return result;
  }
  // 三角形面积
  function getTriangleArea(a: number, b: number, c: number) {
    // 海伦公式
    var p = (a + b + c) / 2,
        area = Math.sqrt(p * (p - a) * (p - b) * (p - c));
    return area;
  }
  function isPointInTriangle(
  area1: number,
   area2: number,
   area3: number,
   area: number
  ) {
    return Math.abs(area1 + area2 + area3 - area) < 0.0001; // 这种计算时会有精度问题，会存在在误差。
  }
  return isPointInTriangle(area1, area2, area3, area);
};

向量叉乘

如果有一个 点 O 在 内，那么沿着三角形的边界逆时针走，点 O 一定保持在边界的左边，也就是说 点 O 在边 、、 的左边。

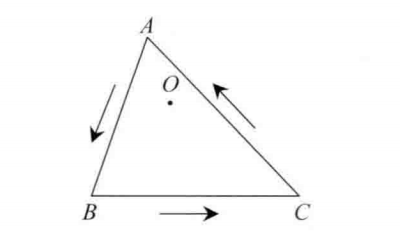
如何判断点在一个边的左侧？

二维向量的叉积公式：

:::info 由于输入的 3个点不一定是逆时针的顺序，比如输入的三点的坐标是 A C B，那就不行了。
所以假设依次输入的点分别为
若 在 的右侧，则表示输入的点的顺序是顺时针，即 A C B 的输入，此时将 调换位置即可保证是逆时针顺序。
:::

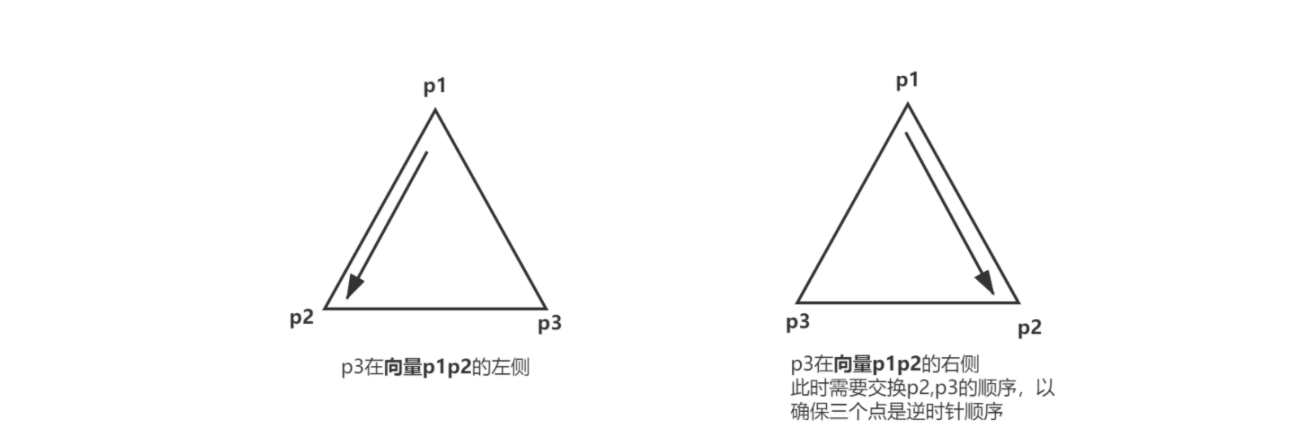interface IPointer {
  x: number;
  y: number;
}
var pointInTriangle = function (
 o: IPointer,
 a: IPointer,
 b: IPointer,
 c: IPointer
): boolean {
  // 计算向量
  function getVector(p1: IPointer, p2: IPointer, p3: IPointer) {
    return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
  }
  function isPointInTriangle(
   p1: IPointer,
   p2: IPointer,
   p3: IPointer,
   o: IPointer
  ): boolean {
    return getVector(p1, p2, p3) < 0 
      ? 
      isPointInTriangle(p1, p3, p2, o) // 三角形三点输入顺序为顺时针
    : getVector(p1, p2, o) > 0 &&
      getVector(p2, p3, o) > 0 &&
      getVector(p3, p1, o) > 0 
  }
  return isPointInTriangle(a, b, c, o);
};