矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇）

来源：Alexander
https://zhuanlan.zhihu.com/p/263777564

〇. 前言

在一个多月前，针对有同学关于矩阵求导中分子布局、分母布局两者的区别的疑问，我写了如下的这篇答案。
矩阵求导中布局约定，两者布局的意义是什么?70 赞同 · 7 评论回答
虽然这篇答案给出了几个结论，但是写的没有很严谨，并没有说明矩阵求导的本质与分子布局、分母布局的本质。
所以，在接下来这篇文章中，我将更严谨地说明矩阵求导的本质与分子布局、分母布局的本质。希望对初学的同学、想理解本质的同学提供一些帮助。
注1：看懂本文只需了解本科阶段高等数学的偏导如何求、本科阶段线性代数的矩阵的定义，无需任何其他知识。
注2：本文若无特殊说明，则约定向量均为列向量，如
注3：本文仅考虑实数，不考虑复数。

一. 函数与标量、向量、矩阵[1]

考虑一个函数

针对 的类型、 的类型，我们可以将这个函数 分为不同的种类。
1、 是一个标量
我们称 是一个实值标量函数。用细体小写字母 表示。
1.1 是一个标量
我们称 的变元是标量。用细体小写字母 表示。
例1：

1.2 是一个向量
我们称 的变元是向量。用粗体小写字母 表示。
例2：设

1.3 是一个矩阵
我们称 的变元是矩阵。用粗体大写字母 表示。
例3：设

2、 是一个向量
我们称 是一个实向量函数 。用粗体小写字母 表示。
含义： 是由若干个 组成的一个向量。
同样地，变元分三种：标量、向量、矩阵。这里的符号仍与上面相同。
2.1 标量变元
例4：

2.2 向量变元
例5：设

2.3 矩阵变元
例6：设

3、 是一个矩阵
我们称 是一个实矩阵函数 。用粗体大写字母 表示。
含义： 是由若干个 组成的一个矩阵。
同样地，变元分三种：标量、向量、矩阵。这里的符号仍与上面相同。
3.1 标量变元
例7：

3.2 向量变元
例8：设

3.3 矩阵变元
例9：设

4、总结

二. 矩阵求导的本质

我们在高等数学[2]中学过，对于一个多元函数
例10：

我们可以将 对 的偏导分别求出来，即：

矩阵求导也是一样的，本质就是 中的每个 分别对变元中的每个元素逐个求偏导，只不过写成了向量、矩阵形式而已。
对于 ，我们把得出的3个结果写成列向量形式：

一个矩阵求导以列向量形式展开的雏形就出现了。
当然我们也可以以行向量形式展开：

所以，如果 中有 个 ，变元中有 个元素，那么，每个 对变元中的每个元素逐个求偏导后，我们就会产生 个结果。
这就是矩阵求导的本质。
至于这 个结果的布局，是写成行向量，还是写成列向量，还是写成矩阵，就是我们接下来要讨论的事情。

三. 矩阵求导结果的布局

不严谨地说，从直观上看：
分子布局，就是分子是列向量形式，分母是行向量形式，如 式。如果这里的 是实向量函数 的话，结果就是 的矩阵了：

分母布局，就是分母是列向量形式，分子是行向量形式，如 式。如果这里的 是实向量函数 的话，结果就是 的矩阵了：

直观上理解了之后，我们针对不同类型的 ，不同类型的变元，给出严谨的布局说明。（这里不讨论标量变元的实值标量函数 ，因为结果就是一个元素嘛~）
1、向量变元的实值标量函数 ,
1.1 行向量偏导形式（又称行偏导向量形式）[3]

1.2 梯度向量形式（又称列向量偏导形式、列偏导向量形式）[4]

这两种形式互为转置。
2、矩阵变元的实值标量函数 ,
先介绍一个符号 ，作用是将矩阵 按列堆栈来向量化。
解释一下，就是把矩阵 的第 列，第 列，直到第 列取出来，然后按顺序组成一个列向量，即：

2.1 行向量偏导形式（又称行偏导向量形式）[3]
即先把矩阵变元 按 向量化，转换成向量变元，再对该向量变元使用 式：

2.2 矩阵形式[3]
即先把矩阵变元 进行转置，再对转置后的每个位置的元素逐个求偏导，结果布局和转置布局一样。

2.3 梯度向量形式（又称列向量偏导形式、列偏导向量形式）[4]
即先把矩阵变元 按 向量化，转换成向量变元，再对该变元使用 式：

2.4 梯度矩阵形式[4]
直接对原矩阵变元 的每个位置的元素逐个求偏导，结果布局和原矩阵布局一样。

2.5 一些发现
2.5.1 转置
式与 式互为转置； 式与 式互为转置。
2.5.2 相等
当矩阵变元 本身就是一个列向量 时， 式、 式、 式相等； 式、 式、 式相等；当然，前三个式子与后三个式子互为转置。
这一发现说明，对于向量变元的实值标量函数 , ，结果布局本质上有两种形式，一种是 矩阵（已经成行向量了）形式，一种是梯度矩阵（已经成列向量了）形式。两种形式互为转置。
3、矩阵变元的实矩阵函数 , ，
3.1 矩阵形式[5]
即先把矩阵变元 按 向量化，转换成向量变元：

再把实矩阵函数 按向量化，转换成实向量函数：

这样，我们就把一个矩阵变元的实矩阵函数 ，转换成了向量变元的实向量函数 。接着，对照 式写出结果布局为 的矩阵：

3.2 梯度矩阵形式[6]
即先把矩阵变元 按 向量化，转换成向量变元：

再把实矩阵函数 按向量化，转换成实向量函数：

这样，我们就把一个矩阵变元的实矩阵函数 ，转换成了向量变元的实向量函数 。接着，对照 式写出结果布局为 的矩阵：

3.3 一些发现
3.3.1 转置
式与 式互为转置。
3.3.2 相等1
当实矩阵函数 本身是一个实值标量函数 时， 式、 式相等； 式、 式相等；当然，前两个式子与后两个式子互为转置。
这一发现说明，对于矩阵变元的实值标量函数 , ，结果布局本质上有四种形式，第一种是 矩阵（已经成行向量了）形式，第二种是梯度矩阵（已经成列向量了）形式，第三种是 矩阵（就是矩阵）形式，第四种是梯度矩阵（就是矩阵）形式。第一种和第二种形式互为转置，第三种和第四种形式互为转置。
3.3.3 相等2
当矩阵变元 本身就是一个列向量 时， 同时实矩阵函数 本身是一个实值标量函数 时， 式、 式、 式、 式相等； 式、 式、 式、 式相等；当然，前四个式子与后四个式子互为转置。
这一发现仍说明，对于向量变元的实值标量函数 , ，结果布局本质上有两种形式，一种是 矩阵（已经成行向量了）形式，一种是梯度矩阵（已经成列向量了）形式。两种形式互为转置。
4、矩阵变元的实向量函数 、向量变元的实向量函数 、向量变元的实矩阵函数
这三个都可以看做是矩阵变元的实矩阵函数 ，可使用3、进行计算（因为向量就是一种特殊的矩阵）。

四. 分子布局、分母布局的本质

看到这里，相信同学们对矩阵求导结果的布局有了很全面的了解了，无非就是分子的转置、向量化，分母的转置、向量化，它们的各种组合而已。
结合上述知识，我们总结：
1、分子布局的本质：分子是标量、列向量、矩阵向量化后的列向量；分母是标量、列向量转置后的行向量、矩阵的转置矩阵、矩阵向量化后的列向量转置后的行向量。包含 式、 式、 式、 式。
2、分母布局的本质：分子是标量、列向量转置后的行向量、矩阵向量化后的列向量转置后的行向量；分母是标量、列向量、矩阵自己、矩阵向量化后的列向量。包含 式、 式、 式、 式。
思考一下，其实我们可以再简洁一些：谁转置了，就是另一方的布局。分子转置了，就是分母布局；分母转置了，就是分子布局。
最终，我们列一个表格，总结分子布局、分子布局的本质：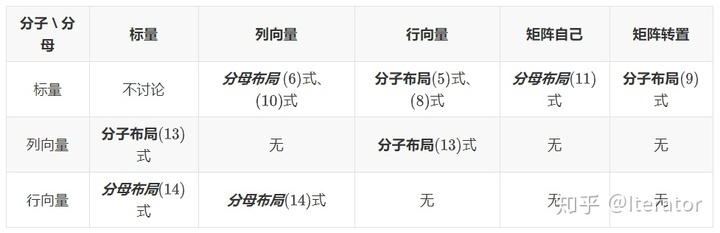

五. 完

本文到这里就结束了，希望对大家有帮助。如果有时间的话，后面我会再发一篇文章，来进行若干常见矩阵求导公式的数学推导。欢迎大家点赞、关注、收藏、转发噢~

矩阵求导系列其他文章：
对称矩阵的求导，以多元正态分布的极大似然估计为例（矩阵求导——补充篇） - Iterator的文章 - 知乎
矩阵求导公式的数学推导（矩阵求导——进阶篇） - Iterator的文章 - 知乎
矩阵求导公式的数学推导（矩阵求导——基础篇） - Iterator的文章 - 知乎

参考

1. ^张贤达《矩阵分析与应用（第二版）》P143
2. ^《高等数学 同济大学第七版 下册》P66
3. ^abc张贤达《矩阵分析与应用（第二版）》P144
4. ^abc张贤达《矩阵分析与应用（第二版）》P146
5. ^张贤达《矩阵分析与应用（第二版）》P145
6. ^张贤达《矩阵分析与应用（第二版）》P147

编辑于 2020-11-24 10:27