老师不会教你的理(biàn)论(fēn)力(yuán)学(lǐ)part3.泛函与变分

来源：https://zhuanlan.zhihu.com/p/268326255
作者：灵动之翼
物理学专业，喜欢数学和物理方面的问题，也喜欢科幻、逻辑推理
关注他

这一部分呢，我们就讲讲虚位移的数学本质。
温馨提示：本部分的数学内容会很多，不过只要学过高等数学，这些推导都可以理解。
那么坐稳了，我们现在就出发啦！
在上一部分我们已经知道，虚位移的数学本质就是变分。但是，变分又是什么呢？如上一部分所言，它是不是一个“耍无赖”的定义？为此，我们要先介绍泛函的概念。
简单地说，泛函就是“函数的函数”，它把一个函数映射到一个数。一般的函数，是“进去一个数（自变量），出来一个数（因变量）”，泛函则是“进去一个函数，出来一个数”。比如，定积分 就定义了一个以函数 为自变量的泛函 ，不难看出，它的确是“进去一个函数，出来一个数”的，而且注意一点： 的值与 的取值无关，而仅与 在 这一段的取值有关。我们把 叫做泛函 的宗量，以区别于自变量 。
变分 则相当于泛函中的微分 。我们知道，函数值的变化量 ，当自变量的改变量 很小时， 与 近似相等。变分也差不多，比如泛函 ，它的改变量就是 ，这里 和 是两个不同的函数， 就是宗量函数的改变量。显然，宗量函数的改变量本身也是一个函数。
那么，如果宗量函数的改变量 很小，泛函就和它的变分 近似相等……打住！“宗量函数的改变量”本身也是一个函数，它怎么才算“小”？
为此，我们必须引入函数距离的概念。
定义：若函数 和 在区间 上存在 阶导数，则称 为函数 和 的 级距离。
特别地，当 时， 是函数 和 的0级距离。

从几何直观来看，函数的0级距离就是两个函数“高度差”的最大值。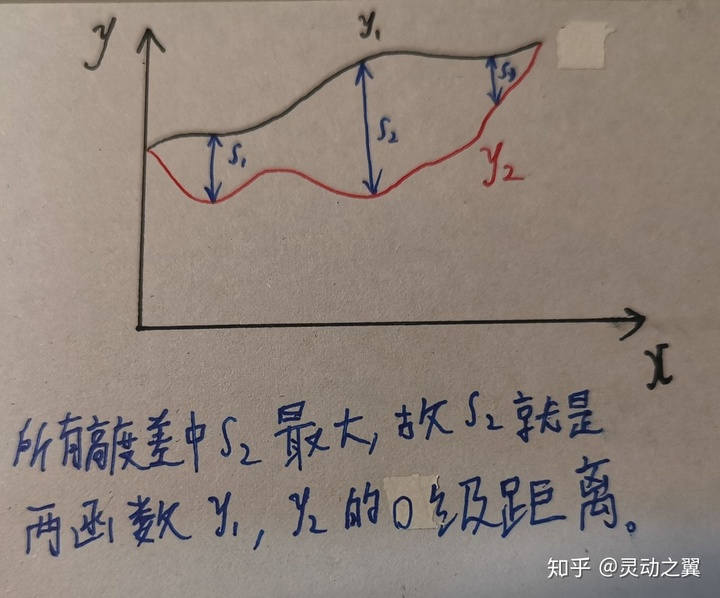

以下我们就直接把“0级距离”简称为函数的“距离”啦。
仔细想想，这样一个定义保证了几个结果：

1. 函数的距离永远非负，当且仅当两个函数相等时，距离为0。
2. 函数 和 的距离= 和 的距离。
3. 三角不等式。

这些都是符合我们对“距离”的直观理解的。（事实上这些正是泛函分析中的“距离空间”必须满足的要求）
那么，宗量函数的改变量很小，自然就是指 和 的距离很小啦。
我们知道一般的函数，对自变量来说， ，即自变量的微分和变化量等价，所以我们可以用微分来表示自变量的变化量。泛函也一样，只不过此时的自变量变成了宗量 ，微分变成了变分，那么我们显然也可以用变分 来表示 的变化量。
这样一来，泛函 的变分，不用我说你应该也知道，它就是 的线性部分啦。但是等等，线性部分？我们知道微分是函数变化量的线性部分，因为 是关于 的线性函数，但是泛函……怎么样才算线性泛函？似乎不太直观。不过我们再仔细想想，线性的定义不就是满足线性运算吗？那么，线性泛函也就很好定义啦。
定义：若连续泛函 满足 和 ，其中C为任意常数，则称 为关于 的线性泛函。
理论力学中，常常把某个量看做坐标与时间的函数，比如第一部分中提到的 ，而拉格朗日函数 更是关于所有广义坐标和它们一阶导数的函数，同时广义坐标 以及它们的导数 也都是关于 的函数。为了与理论力学接轨呢，我们就来研究一下 这类……它算不算泛函？好像宗量既有函数又有普通的字母啊。好吧，其实我也不知道算不算，但这并不影响我们研究它。这里先提醒一下， 都是独立的变量，互相不影响，如果你看过第一部分的预备知识呢，这应该不难理解啦。
那么像这类函数，它的变分是什么呢？应该是 的线性部分……咦？为什么最后面的 不跟着变分？它被抛弃了？难道自变量在变分中不配拥有姓名？

嘿，怎么这么没骨气呢！既然你觉得自变量不配，那我包装一下自己，把 换成一个函数 ，这样原函数变成多元泛函 ，这样总可以变分了吧？
呃，对不起，您还是不配（狗头保命）。

为什么呢？哈哈，还记得上一部分那个用魔法也移动不了的物体吗？由于约束条件过强，它没有虚位移。在数学上其实就是因为，宗量函数是一个不定的函数，这样才可以改变，像 这样的函数，它已经是一个确定的函数了，就不能再改变了，也就是说它的变分 恒为零。
为了更好地理解这类函数为什么不配拥有姓名（），我们还是类比一下一般函数的微分。
比如 ，则它在 上有导数，在任意区间上也有导数，但是对一个确定的 ，比如规定 ，那么就恒有 ，这时的函数在图像上只剩下一个点，它还有导数吗？显然没有了吧。泛函变分也一样，只是我们通常只会把一个确定的常数当做不变量，而不会想到一个确定的函数也是不变量。
好了，接着说，现在我们已经知道为什么 就是 的线性部分了，但一个泛函的变分如果就写成这样，显然不能用来做什么，我们要把它算出来才行。嗯，这里我们就先不列出推导过程(将在以后的补充部分中给出），直接告诉大家，算出来的结果就和微分具有相同形式，即

是不是长得很好看？嗯，至少很好记，哈哈。其实这也就是理论力学教材中说变分作用在空间变量上和微分完全相同的原因。那么我现在考考你， ， 这些玩意儿是什么？我们知道 本身也是函数，函数对函数求偏导，这是个什么东西？
哎，对了，这也就像我在第一部分说的那样，此时我们已经不再把 和 看作函数了。严格来说，这是把泛函 中出现的所有 换成一个自变量u，所有 换成另一个自变量 ，并对函数 求偏导。或者呢，我们就强行认为 是可以任意由我们控制的自变量，如下粗暴地理解：

嗯对，就是偏导数的定义式。
讲到这里，你应该已经知道理论力学中说变分“作用在空间变量上与微分相同，作用在时间变量上则为0”是怎么回事啦。它的确不是一个耍无赖的定义吧，只是作用在函数上与微分相似，作用在自变量上为0而已。是不是很神奇呢？
另外，变分还有一个性质，就是泛函取极值的点变分必为0。这一点也和一般函数的微分类似，我们也将在补充部分中给出它的证明。这个性质比较重要，在以后的学习中要用到。
现在知道了虚位移的数学本质，那我们就从数学角度来比较一下虚位移和实位移吧。
以一维运动为例，一个物体的位置 是时间 的函数，即 ，它有对应的函数图像。所谓实位移，就是沿着函数图像走的一段路，即 。虚位移 呢，则是函数整体移一小段位置后，同一个t对应的函数值的变化量。如图所示(注意颜色，绿色的是虚位移，蓝色的是实位移)。

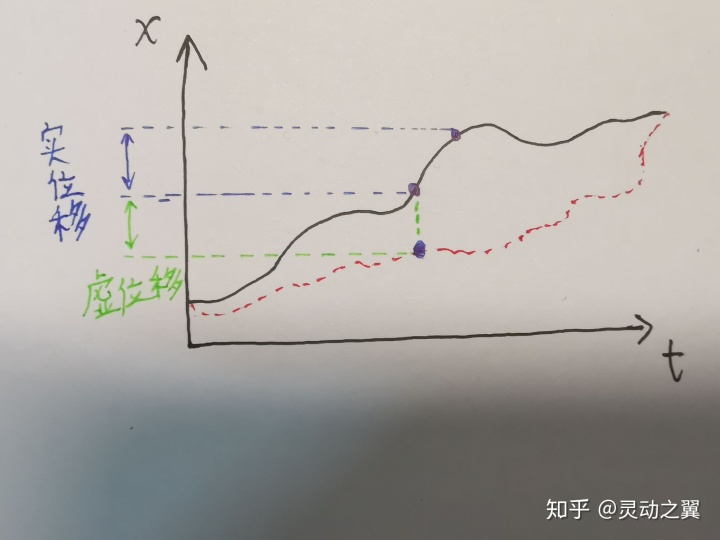
所以正如我在上一部分说的，虚位移和实位移没有什么必然联系，它们是完全不同的概念。
那么本部分的内容就是这些啦。学了这一部分以后，是不是对虚位移有了更深入的理解了呢？

参考文献：
金尚年 马永利《理论力学》
刘川《理论力学讲义》
老大中《变分法》
赵焕光《泛函分析入门》
编辑于 2022-04-02 17:51