原文链接：https://zhuanlan.zhihu.com/p/410349561

    对于基于塑性力学框架中的材料本构模型，应力更新和相关变量（等效塑性应变或者塑性做功）是必不可少的环节。利用隐式（后欧拉）算法更新应力和相关变量在理论上具有无条件稳定的优势。在塑性力学相关的文献里，隐式（后欧拉）算法的实现往往需要利用牛顿-拉弗森迭代（NR）。对于一个完整的隐式集合，在每一个荷载（时间）步内，我们需要为本构模型计算（更新）三个值，首先是利用 elastic predictor – plastic corrector 方法计算出应力，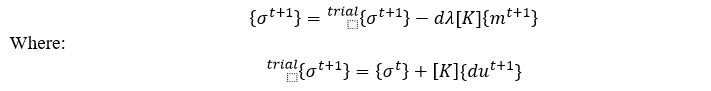
    image.png
    同时要考虑相关变量的更新，这里选用塑性做功：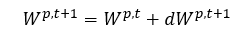
    image.png
    最后，判断更新得到应力和塑性做功是否满足屈服方程：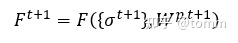
    image.png
    需要注意的是，应力和塑性做功方程的右边的参数也是关于应力和塑性做功自身的表达式，即，这些方程是隐式的：
    image.png
    为了解决隐式问题，需要用到牛顿-拉弗森迭代。如果只需要通过迭代一个数（通常是塑性算子增量）从而更新整个隐式系统，算法为：
    image.png
    如果要一次性同时更新所有参数，包括应力、塑性功和塑性算子增量，NR算法写为：
    image.png
    单个方程（One equation）
    对于只更新塑性算子增量的情况，首先要计算应力和塑性功，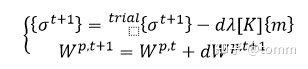
    image.png
    然后将应力和塑性功带入屈服面方程：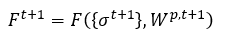
    image.png
    这时候的雅可比是一个数值，即屈服方程对塑性算子增量的梯度，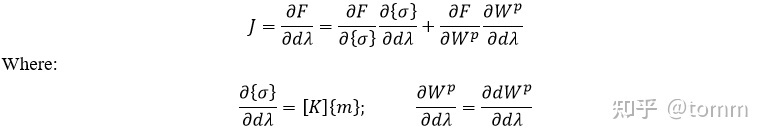
    image.png
    整体式（Monolithic）
    另一种选择是将应力、塑性功和塑性算子增量集合成一个数列，它们对应的计算公式可以组合成一个残差集合：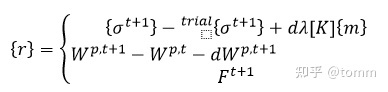
    image.png
    相应的雅可比矩阵为，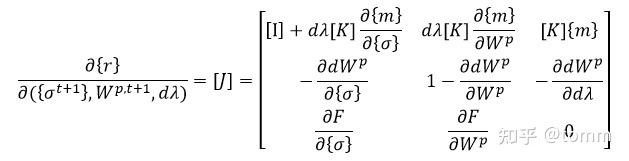
    image.png
    注意雅可比方程的右下脚为零，即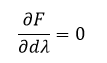
    image.png
    连续式（Sequential）
    对于更新相关变量非常复杂的模型，通常在不同方向、不同荷载步含有多个变量，因此雅可比矩阵会较为巨大，容易导致逆矩阵发散。因此可以将需要更新的场变量从残差集合中取出，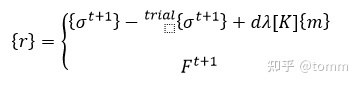
    image.png
    雅可比矩阵写为，
    image.png
    那么，如何定义雅可比矩阵右下角的参数？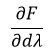
    image.png
    这里给出的计算式为，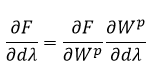
    image.png
    不同于单个方程（One equation）迭代更新的情况，这里的雅可比矩阵已经对应力更新，所以屈服方程 F 中的应力不包含塑性算子增量。也不同于装配式（Monolithic）迭代更新的情况，由于雅可比没有对塑性功更新，所以屈服方程 F 中的塑性功需要包含塑性算子增量。
    单独更新塑性功，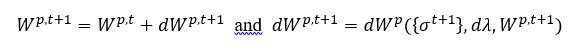
    image.png
    塑性功增量是一个关于塑性功自己的函数，所以塑性功的隐式表达为，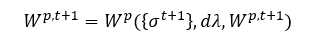
    image.png
    验证
    为了验证雅可比矩阵右下角的屈服方程对塑性算子增量的梯度函数，我们对比它们迭代过程中得到的屈服方程 F 的表达式，
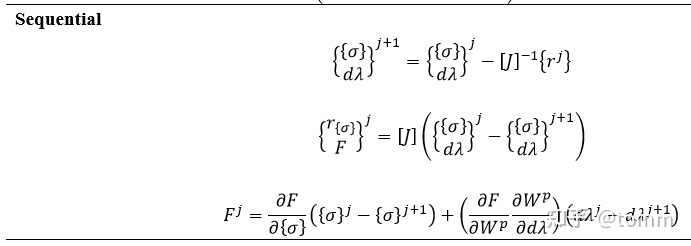
    image.png
    image.png
    image.png
    由于塑性算子增量的增量可以写做，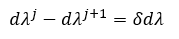
    image.png
    所以，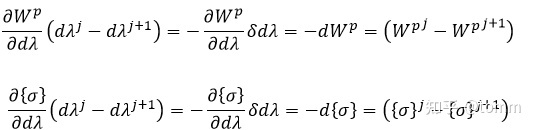
    image.png
    结合前面的三种更新方法得到的 F，我们可以确认它们的最终表达式相同，
    image.png