原文链接：https://zhuanlan.zhihu.com/p/496031630
    在塑性力学中，由于材料应力状态的复杂性，单一的屈服面无法完整体现材料的应力特性，因此多个屈服面组成的本构模型经常出现在岩土或者各项异性的材料（比如木材）的模拟中。最经典的莫过于摩尔库伦本构。但是摩尔库伦本构是非常特殊的，因为在deviatoric平面内，各个屈服面之间的夹角是确定。而且各个屈服面是平直的，所以可以采用各种特殊的手法简化应力回归。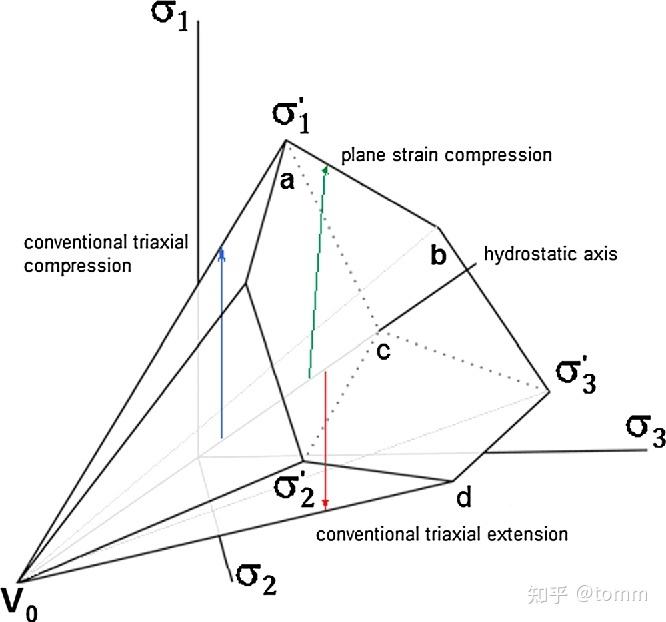
    image.png
    对应考虑了材料受压破坏的本构模型，控制受压破坏的屈服面和控制拉-剪破坏的屈服面之间的夹角任意的，而且各个屈服面的表面是光滑（凸）弯曲的，所以应力回归的过程就比较复杂。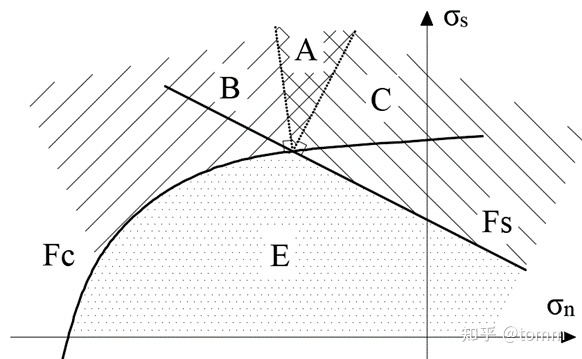
    image.png
    一：前欧拉法
    针对上图中的受压屈服面 Fc 和 Fs，可以给出屈服面的方程，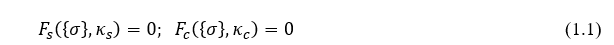
    image.png
    其中sigma为应力，ks 和 kc 为各自屈服面对应的内部变量（可以是等效位移/应变，也可以是做功）。
    这两个屈服面将应力空间划分为4个部分，E 为弹性区间，B 和 C 分别表示受压破坏和受剪破坏区间，A 则是 B 和 C 两个区间的重合部分。理论上，B/C/A 区间都是不存在的，一旦试应力点位于 B 区间应力需要回归到Fc屈服面，一旦试应力点位于 C 区间应力需要回归到 Fs屈服面，一旦试应力点位于 A 区间应力需要回归到 Fc 和 Fs 的交点。
    对于交点处的情况，塑性应变或者塑性位移可以计算为，
    image.png
    因此应力增量的计算表达式可以写为，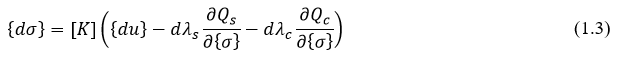
    image.png
    对于屈服面Fs，将其对（伪）时间求导，得到 consistency condition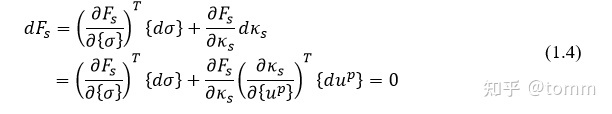
    image.png
    将（1.2）带入到（1.4）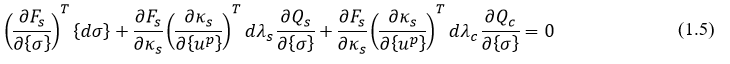
    image.png
    （1.5）中后面两个式子可以写为，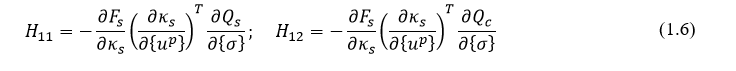
    image.png
    把（1.3）带入到（1.5）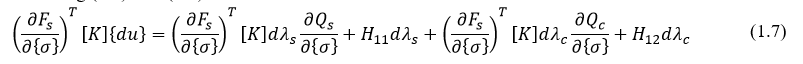
    image.png
    同理，对屈服面 Fc 进行类似的步骤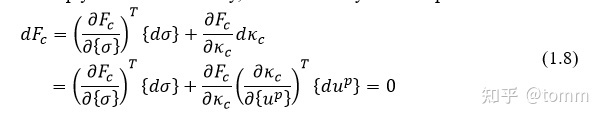
    image.png
    把（1.2）带入到（1.8）中，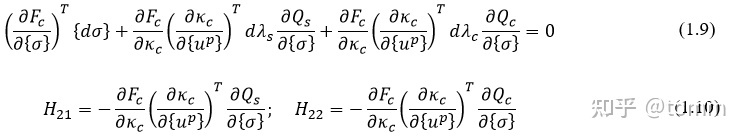
    image.png
    把（1.3）带入到（1.9）中，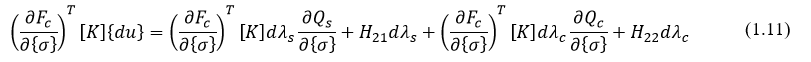
    image.png
    结合（1.7）和（1.11），再写成矩阵形式，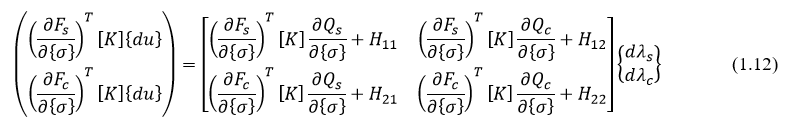
    image.png
    其中，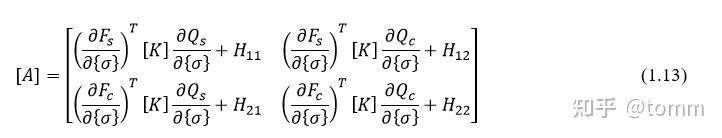
    image.png
    于是，两个屈服面的塑性增量因子可以计算为，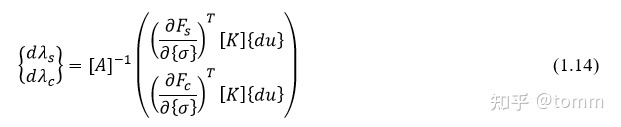
    image.png
    大致的算法实现可以写为，
    image.png
    在具体实现以上算法的时候，我们会发现B区域实际被分为B1和B2区域，C区域实际被分为C1和C2区域。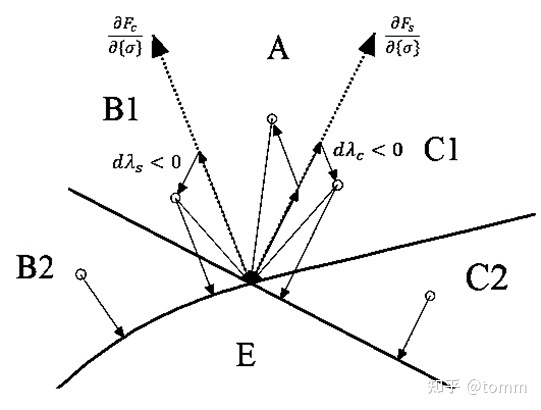
    image.png
    而B1和C1区域的确定，不仅需要计算 Fc 和 Fs，还需要计算各自屈服面的塑性增量的数值。
    image.png
    总的计算流程可以表示为，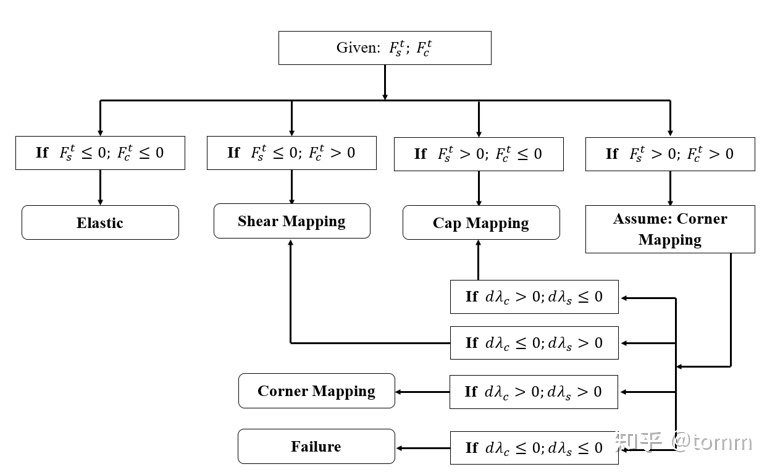
    image.png
    当应力位于B和C区域时，应力回归过程会用到的变量计算式子，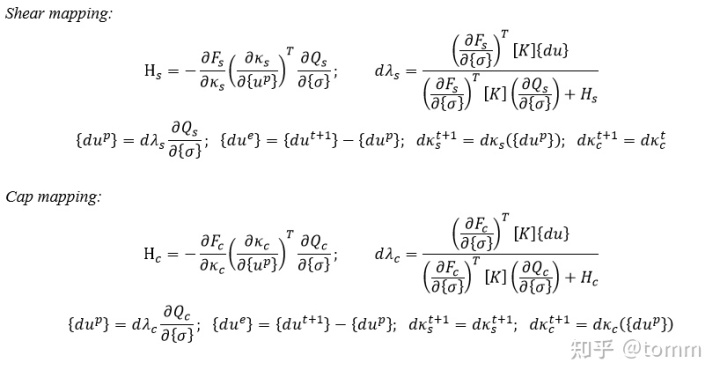
    image.png
    基于前面的算法，我们进行改进，对B1和C1区域进行细分，得到新算法
    image.png
    二：后欧拉法
    隐式算法在处理多屈服面时更加复杂，因为隐式算法通常需要采用牛顿拉弗森迭代计算塑性增量因子，又因为前面提到的塑性增量因子的±号会改变应力回归的回归方向（回归位置可能从交点换到某个屈服面）。Simo和Hughes（2006）的书（computational inelasticity）给出了两种策略：
    image.png
    前者在牛顿迭代结束后再根据塑性增量的数值决定应力回归的指向，后者则在每次迭代时都考虑应力回归指向的变更。第二种方案采用的文献更多，大致的算法为，
    image.png
    另一方面，考虑到屈服面的位置会随着内部变量发生改变，所以对需要对计算得到的新屈服面进行二次判断，否则会出现错误的回归。如下图，假设 Fc （F2）的不会发生变化，Fs（F1）会随着内部变量的增加而收缩。在迭代 j 步时，应力本应该回归到 F2，但同时 F1 出现收缩，新的应力需要回归到 F1了。这点是Simo的方法里没有考虑到的。Macorini 和 Izzuddin (2011) 的论文考虑屈服面收缩的问题，但是没有对塑性增量因子的±符号进行考虑。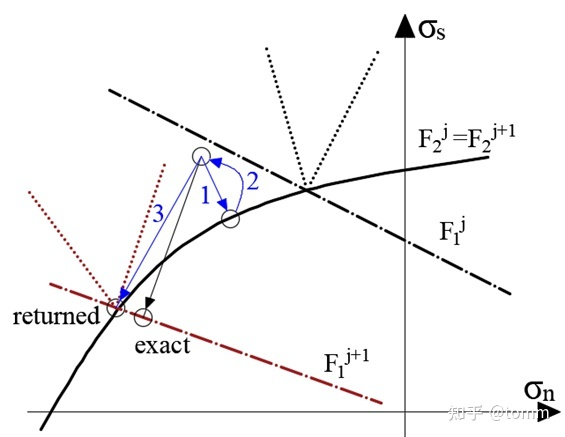
    image.png
    我们将两个方案结合起来，得到更为全面的应力回归流程，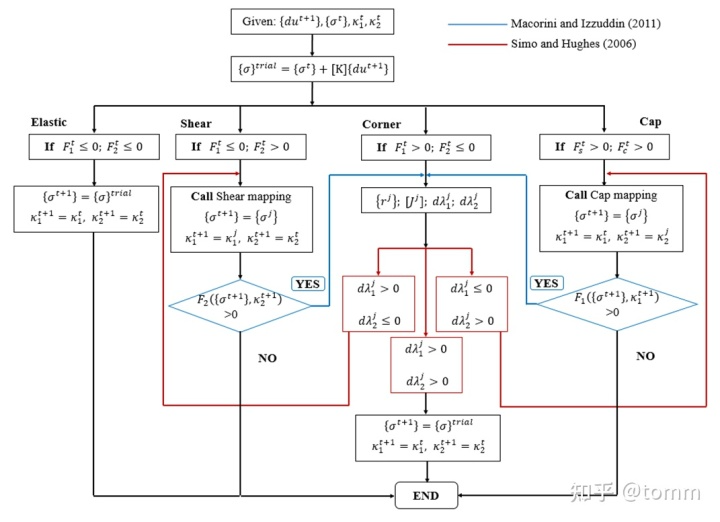
    image.png
    将以上流程图以算法的形式表达为，
    image.png
    其中屈服面上的回归计算过程为，
    image.png
    三：使交点光滑化
    如果将交点光滑化，可以免去交点处的特殊回归过程。这种方案通过改动本构简化数值实现，很受青睐。以下图中的三屈服面本构为例，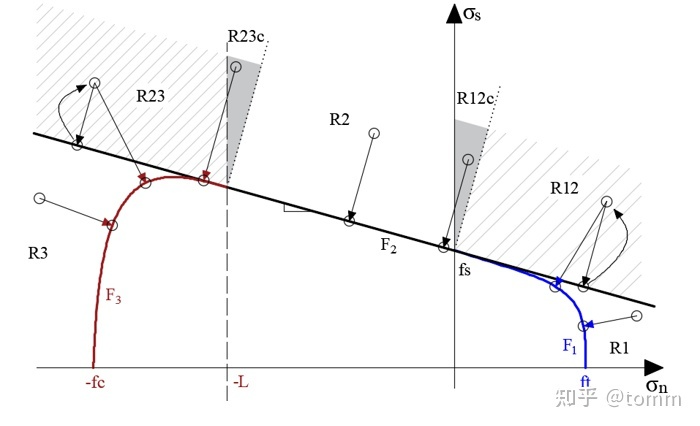
    image.png
    三个屈服面的表达式可以写为，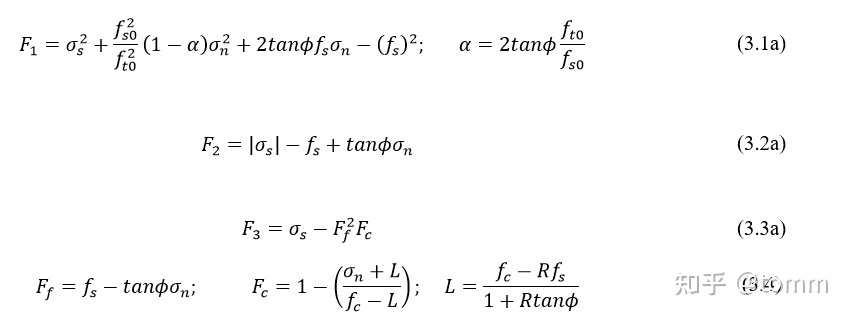
    image.png
    控制三个屈服面收缩过程的（强度）软化系数为，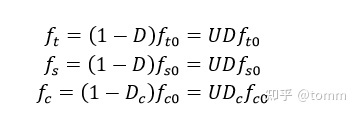
    image.png
    带入到（3.1)-(3.3），得到新的表达式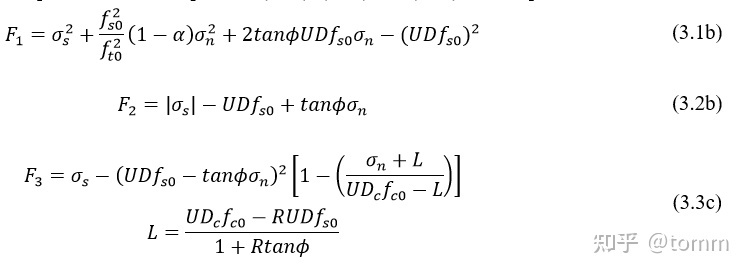
    image.png
    不同R参数对受压屈服面的影响，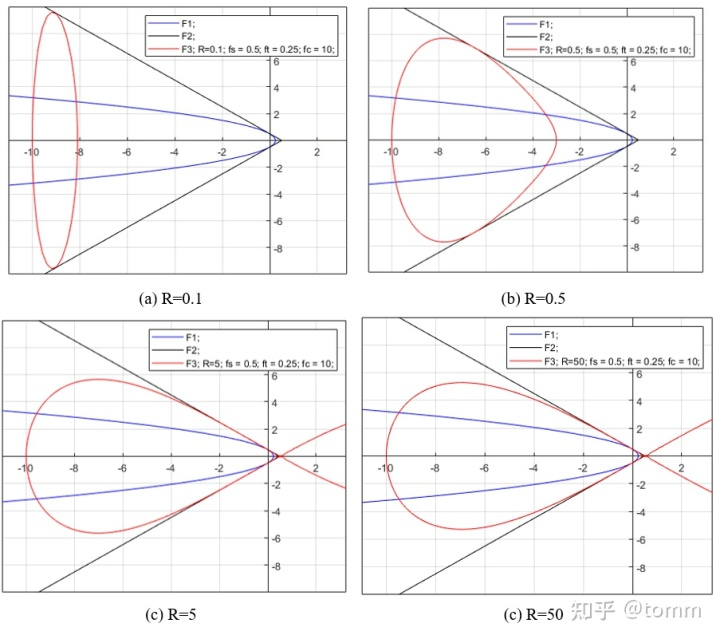
    image.png
    不同alpha参数对拉-剪屈服面的影响，
    image.png
    基于位移的损伤因子可以写为，
    image.png
    基于做功的损伤因子可以写为，
    image.png
    做功的计算表达式为，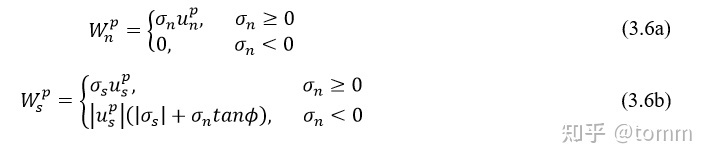
    image.png
    为了让受压屈服面（cap model）可以出现强化-软化过程，对于受压强度的定义为，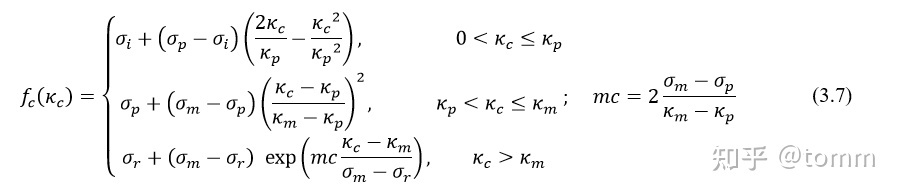
    image.png
    因此非损伤因子的计算为，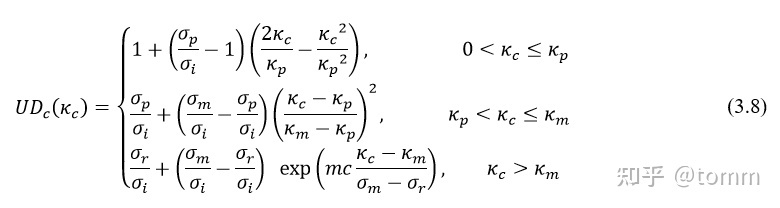
    image.png
    大致的算法为，
    image.png
    发布于 2022-04-10 13:59