摘自:「百度百科」
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。直到1948年,香农提出了「信息熵」的概念,才解决了对信息的量化度量问题。信息熵这个词是香农从热力学中借用过来的。热力学中的热熵是表示分子状态混乱程度的物理量。香农用信息熵的概念来描述信源的不确定度。信息论之父香农第一次用数学语言阐明了概率与信息冗余度的关系。
理解信息量
「【如何理解信息熵-哔哩哔哩】https://b23.tv/23HmhK」
如果使用电位信号「0或1」在两个相互隔离的房间交流结果
- 那么抛掷一枚硬币有两种可能性「正面或反面」需要发送「1」个电位信号 | 1 | 正面 | | —- | —- | | 0 | 反面 |
- 那么抽取一张有四种不同花色扑克「♠2、♥2、♣2、♢2」需要发送「2」个电位信号 | 00 | ♠2 | | —- | —- | | 01 | ♥2 | | 10 | ♣2 | | 11 | ♢2 |
- 那么选择一个有八个不同区域大转盘「赤、橙、黄、绿、青、蓝、紫、白」需要发送「3」个电位信号 | 000 | 赤 | | —- | —- | | 001 | 橙 | | 010 | 黄 | | 011 | 绿 | | 100 | 青 | | 101 | 蓝 | | 110 | 紫 | | 111 | 白 |
信息的价值在于「消除不确定」:
- 传递抛掷硬币结果信息消除「两种」情况中「出现哪一个面」的「不确定性」。
- 传递抽取扑克结果信息消除「四种」情况中「出现哪种花色」的「不确定性」。
- 传递选择转盘结果信息消除「八种」情况中「出现哪个区域」的「不确定性」。
如果把系统中所有「等概率事件」的数量取以「2为底」的对数,刚好是传递这个事件结果所需要的电位信号数量:
| 等概率事件数量 | 电位信号(信息量) | |
|---|---|---|
| 硬币 | 2 | Log2(2) = 1 Bit |
| 扑克 | 4 | Log2(4) = 2 Bit |
| 转盘 | 8 | Log2(8) = 3 Bit |
- 那么抛掷一个有六个不同点数的骰子「1、2、3、4、5、6」需要发送「?」个电位信号
按照信息论的公式「Log2(6) = 2.58 Bit」,但工程上不具备可实施性向上取整为「3 Bit」,浪费「0.48 Bit」。
信息论对信息度量方式刻画了一个事实:
- 系统中等概率事件「越多」,那么传输其中一个事件的信息量「越大」。
- 系统中等概率事件「越多」,那么哪个事件所发生的不确定性「越大」。
也可以看做是对信号源「不确定性」的刻画,那么度量不确定性的信息量称之为「信息熵」。
信息熵案例
之前的案例提到的都是「等概率事件」,但真实世界并不都是「等概率」的。例如抛掷一个「正面概率20%,反面概率80%」的「作弊」硬币时,那么我们需要把「20%」和「80%」拆分为「两组」等概率事件。将一个「非等概率事件」系统拆分为两个「等概率事件」系统。
| 1/0.2 = 5 | 想象成由「5」个球的摸球系统中摸出球的概率 | Log2(5) |
|---|---|---|
| 1/0.8 = 1.25 | 想象成由「1.25」个球的摸球系统中摸出球的概率 | Log2(1.25) |
面对等概率事件系统就很容易计算信息熵。将两个转化后等概率事件系统「信息熵相加」就是不均匀硬币的信息熵:
当然两个等概率系统本身出现的概率也不一样,所以需要将两部分分别乘以他们「出现的概率」:
如果用数学符号替换以上具体的值就是这样:
当然更通用「信息熵」公式是这样:
可以看出信息熵是给每个概率值转换后等概率事件摸球系统的「信息值」或者说「期望」。所以这个案例的信息熵约等于「0.72」Bit,意味着只要「0.72」Bit的信息量就可以将这个做了手脚的硬币的结果传输出去。由于工程上的不可实现,我们还是需要使用「1」Bit进行传输。
-0.2 * log2(0.2) - 0.8 * log2(0.8);public static Double log2(Double n) {return Math.log(n) / Math.log(2);}
信息熵应用
如同光速在物理学中作为速度的极限,信息熵指出了通讯极限或者数据压缩效率极限,一切想突破这个极限的行为都是无用功。正如之前所说正反两面出现概率为「0.2」和「0.8」的硬币,信息熵告诉我们只需「0.72」Bit就可以将结果传输出去,但碍于工程实现我们只能用「1」Bit。那么如果是更多可能的数据源,那可以通过某种编码方式进行压缩从而降低传输或存储成本。
同样基于信息论原理可知,信息熵也是对「随机事件不确定性」极佳的度量方式。比如信息熵可以用于衡量的指定特征能够为「分类系统」带来「多少信息」,带来信息越多该特征就「越重要」。
- 由信息熵计算公式可知其取值范围为「0 ≤ H(X) ≤ Log2(N)」
那么如果随机事件服从「均匀分布」时事件的「不确定性最大」为「H(X) = Log2(N)」。
double[] p = new double[] { 1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d };
double x = 0d;
for (double pi : p) {
x += pi * log2(pi);
}
// 相同
System.out.println(log2(6d));
System.out.println(-x);
public static Double log2(Double n) {
return Math.log(n) / Math.log(2);
}
但是如果随机事件并非「均匀分布」,那么事件的「不确定性变小」。
double[] p = new double[] { 30 / 60d, 15 / 60d, 5 / 60d, 5 / 60d, 5 / 60d, 40 / 60d };
double x = 0d;
for (double pi : p) {
x += pi * log2(pi);
}
// Log2(6d) > -x
System.out.println(log2(6d));
System.out.println(-x);
条件熵
正如「信息熵」量化随机变量的不确定性,「条件熵」量化的是一个「条件」下随机变量的不确定性。
摘自:「百度百科」
条件熵 H(X|Y)表示在已知随机变量Y的条件下,随机变量X的不确定性。
如同信息熵公式,条件熵也有其计算公式: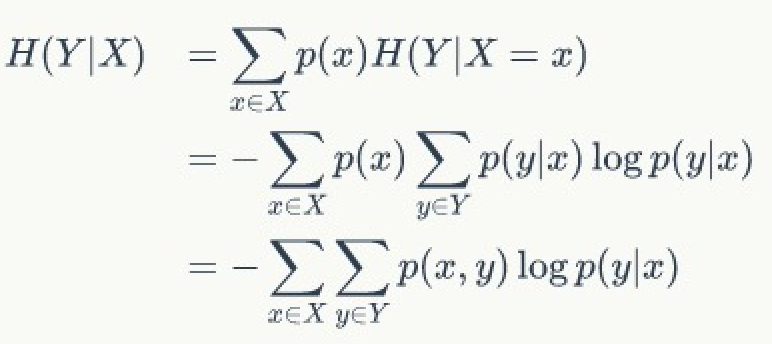
可以通过一个案例来理解:如果一批骰子有「一半做工出现问题」无法掷出1和6,其他4个数字概率平均分布。那么在已知「一半做工出问题」前提下,抛掷骰子的结果的不确定性是多少呢?可以抽象问题为在已知「随机变量X」的条件下「随机变量Y」不确定性的度量问题。
- 那么随机变量X服从「P(X = xi) ∈ {1:标准骰子,2:问题筛子} 的概率为(1/2,1/2)」 | P(Y|X = 标准骰子) ∈ {2,3,4,5} | 概率为(1/6,1/6,1/6,1/6) | | —- | —- | | P(Y|X = 问题骰子) ∈ {2,3,4,5} | 概率为(1/4,1/4,1/4,1/4) |
那么根据公式可知:
- H(Y|X) = - ΣPi(X) ΣP(Y|X) Log2(P(Y|X))
- X = xi = 标准骰子,Y = 2,3,4,5
- ΣP(Y|X = xi) Log2(P(Y|X = xi)) = Σ1/6 Log2(1/6) = Σ-1/6 Log2(6) = *-Log2(6)
- -ΣP(X = xi) ΣP(Y|X = xi) Log2(P(Y|X = xi)) = 1/2 * Log2(6)
- X = xi = 问题骰子,Y = 2,3,4,5
- ΣP(Y|X = xi) Log2(P(Y|X = xi)) = Σ1/4 Log2(1/4) = Σ-1/4 Log2(4) = *-Log2(4)
- -ΣP(X = xi) ΣP(Y|X = xi) Log2(P(Y|X = xi)) = 1/2 * Log2(4)
- 那么「H(Y|X) = 1/2 Log2(6) + 1/2 Log2(4)」就是按案例的「条件熵」。
- X = xi = 标准骰子,Y = 2,3,4,5
信息增益
摘自:「百度百科」
在概率论和信息论中信息增益是非对称的,用以度量两种概率分布P和Q的差异。信息增益描述了当使用Q进行编码时再使用P进行编码的差异。通常P代表样本或观察值的分布,也有可能是精确计算的理论分布。Q代表一种理论,模型,描述或者对P的近似。
百度百科的解释非常拗口,如果直观解释「信息增益」的作用那么就是:在一个「条件」下信息不确定性「减少」的程度。正如其公式所表示的:
再次回到骰子问题上,如果设定「特征Y」为「一半做工偏差」,「类别X」为「抛掷一次骰子的结果」,那么信息增益就是:
IG(T) = H(X) - H(X|Y) = Log2(6) - (1/2 Log2(6) + 1/2 Log2(4)) = 1/2 Log2(6) - 1/2 Log2(4)
那如果100%骰子都存在上述问题时的信息增益由将如何呢?
设定随机变量X服从「P(X = xi) ∈ {1:问题骰子} 的概率为(1)」
| P(Y|X = 问题骰子) ∈ {2,3,4,5} | 概率为(1/4,1/4,1/4,1/4) |
|---|---|
- ΣP(Y|X) Log2(P(Y|X)) = Σ1/4 Log2(1/4) = Σ-1/4 * Log2(4) = -Log2(4)
- -ΣP(X) = -1
那么此时的「信息增益」就是:
从(Log2(6) - Log2(4) > (1/2 Log2(6) - 1/2 Log2(4)) 可知「案例2」情报的信息增益大于「案例1」。
联合熵
除了条件熵外相关的还有「联合熵」,同样也是一集变量之间不确定性的衡量手段,也是信息熵公式转换的重要步骤之一。联合熵计算公式如下: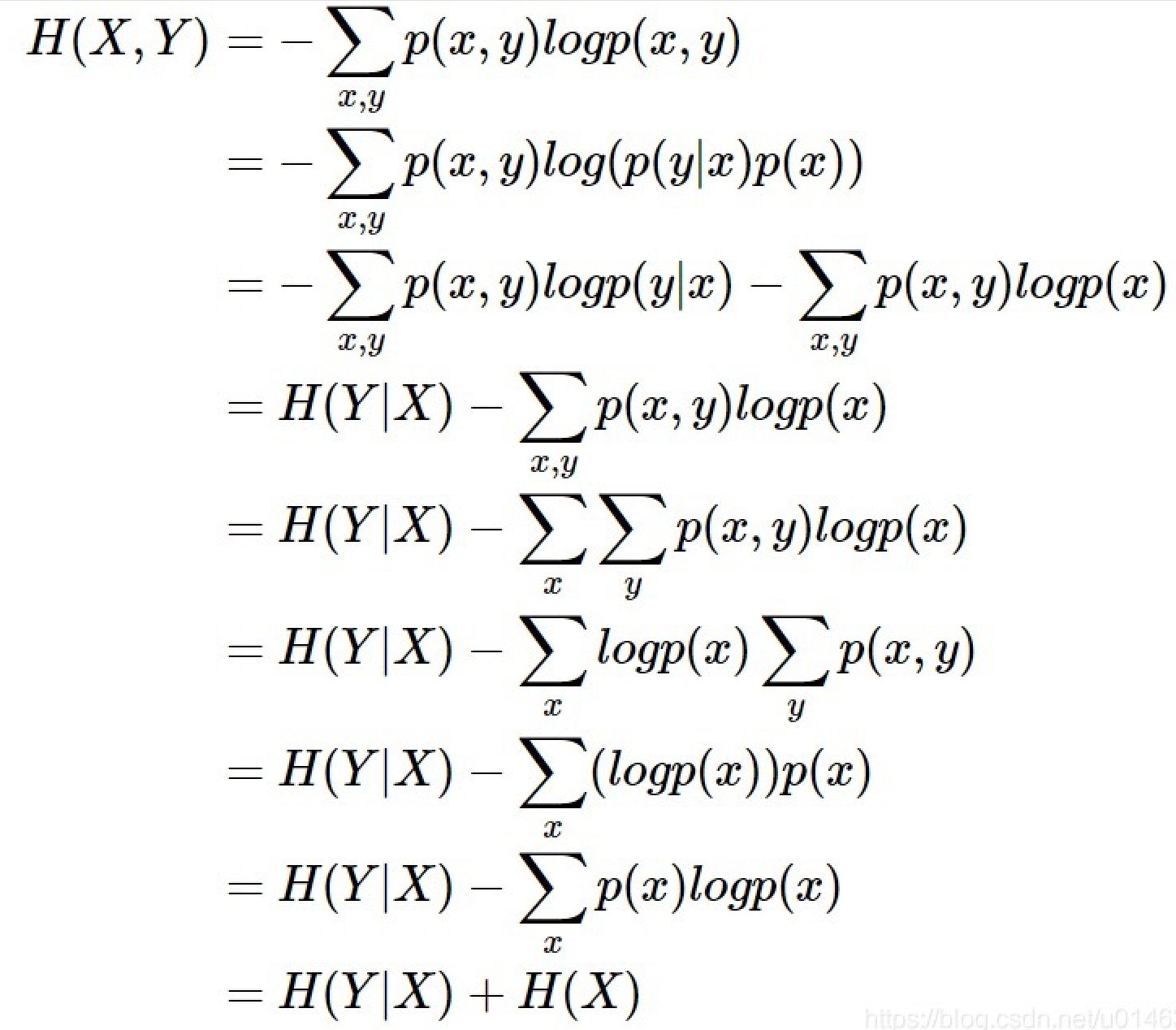
如同概率公式(传送门),熵之间同样可以进行转换:
- H(Y∣X) = H(X∩Y) - H(X)
- H(X∩Y) = H(X|Y) + H(X)
- H(X∩Y) = -ΣPi(X∩Y) * Log2(Pi(X∩Y))
- H(X∩Y) = -ΣPi(X∩Y) Log2(Pi(Y|X) P(X))
- H(X∩Y) = -ΣPi(X∩Y) Log2(Pi(X|Y) P(Y))
相对熵
相对熵又被称为Kullback-Leibler散度(KL散度),是两个概率分布间差异的「非对称性」度量。在信息理论中,相对熵等价于两个概率分布的信息熵的差值。
「相对熵」可以衡量两个随机分布之间的「距离」。当两个随机分布「相同时」相对熵为「零」,两个随机分布的差别「增大时」相对熵也会「增大」,通俗理解就是相对熵是量化两种概率分布P和Q之间「差异」的方式,这是从信息论角度的量化距离而不同于数学概念差距。相对熵的计算公式如下: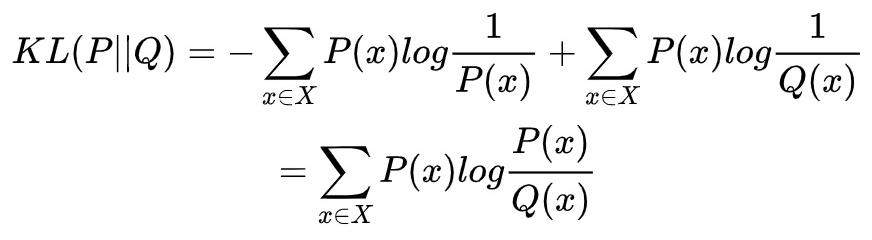
相对熵类似与PSI(群体稳定性)。P(x)表示数据的真实分布,Q(x)表示数据的观察分布。
还是从案例入手:假设一个字符发射器随机发出0和1两种字符,「真实发出概率」分布为A(但实际上不知道A具体分布),同时通过观察可得到的「观察概率分布」为B和C,其他分布如下: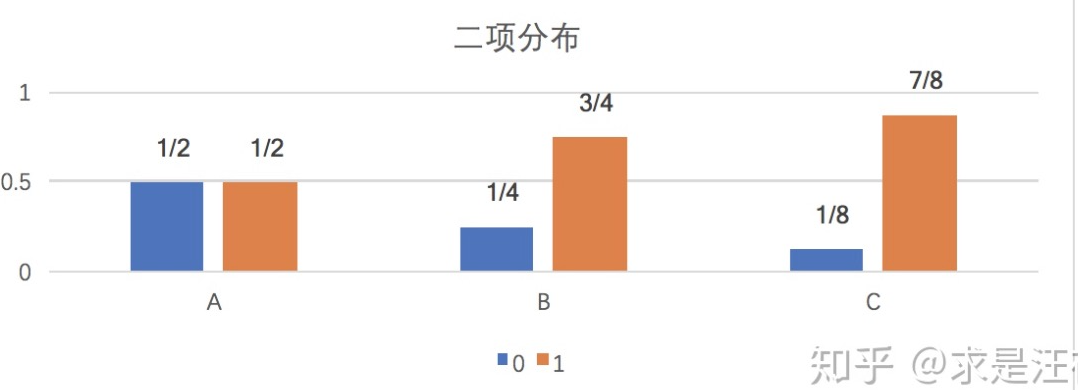
| 分布 | 0字符 | 1字符 |
|---|---|---|
| A | 1/2 | 1/2 |
| B | 1/4 | 3/4 |
| C | 1/8 | 7/8 |
那么应该如何计算「KL散度(相对熵)」呢?
- KL(A||B) = 1/2 Log2((1/2) / (1/4)) + 1/2 Log2((1/2) / (3/4)) = 1/2 * Log2(4/3)
- 1/2 Log2((1/2) / (1/4)) = 1/2 Log2(2)
- 1/2 Log2((1/2) / (3/4)) = 1/2 Log2(2/4)
- Log2(n) + Log2(m) = Log(n * m)
- KL(A||C) = 1/2 * Log2(16/7)
从「KL(A||C) > KL(A||B)」可知,A与B的概率分布在信息量角度更为接近(更吻合)。
如何理解上述计算?
在信息理论中相对熵等价于两个概率分布的信息熵的差值。通俗解释就是概率分布「携带」的信息可以用信息熵衡量,若用观察分布来「描述」真实分布,那么两个分布间还需要多少「额外信息量」呢?

