摘自：「百度百科」

牛顿冷却定律：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

从案例开始

有一杯「87°C」的咖啡放置在一间恒温为「27°C」的房间内。已知「1分钟」后咖啡冷却到「82°C」那么「15分钟」后的温度是多少。此时可以利用牛顿冷却定律计算，即当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比。

  • 牛顿冷却公式

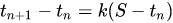
image.png
其中t(n+1)是咖啡在n分钟之后的温度，S是房间的恒定温度，k是比例系数。

  • 根据第1分钟的数据计算比例系数k

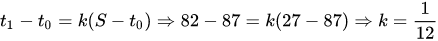
image.png

  • 代入k = 1/12，S = 27

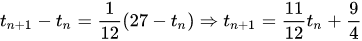
image.png

  • 11/12 Tn + 9/4符合「齐次方程」，代入a > 1的解法

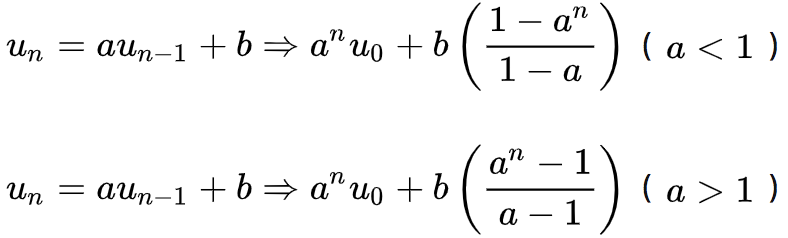
image.png

  • 得到方差 | Un | T(n + 1) | | —- | —- | | U(n -1) | Tn | | a | 11/12 | | b | 9/4 |

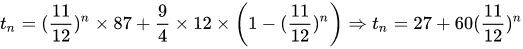
image.png

  • 第15分钟（n = 15）时咖啡的温度是在43.27°C左右，如果时间无限延长，咖啡的最终温度会无限接近室温27°C。

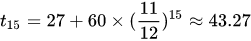
image.png

  • Show Me Thd Code
    1. public static void main(String[] args) {
    2.   double 初始 = 87;
    3.   double 恒定 = 27;
    4.   double 时间 = 15;
    5.   double 冷却 = 5;
    6.   // T1 - T0 = K(S - T0)
    7.   double k = (-冷却) / (恒定 - 初始);
    8.   // T(n + 1) - Tn = k * (恒定 - Tn)
    9.   // T(n + 1) = k * (恒定 - Tn) - Tn = k* 恒定 - k * Tn - Tn = k * 恒定 - Tn * (k - 1) = -(k - 1) * Tn + k * 恒定
    10.   // Un = T(n + 1)
    11.   // U(n - 1) = Tn
    12.   // a = -(k - 1)
    13.   // b = k * 恒定
    14.   double a = -(k - 1);
    15.   if (a < 1) {
    16.       double r = Math.pow(a, 时间) * 初始 + k * 恒定 * ((1 - Math.pow(a, 时间)) / (1 - a));
    17.       System.out.println(r);
    18.   } else {
    19.       double r = Math.pow(a, 时间) * 初始 + k * 恒定 * ((Math.pow(a, 时间) - 1) / (a - 1));
    20.       System.out.println(r);
    21.   }
    22. }

更多用途

牛顿冷却定律本质是「温度」与「时间」的函数，可以用来构建一个「指数式衰减」的过程。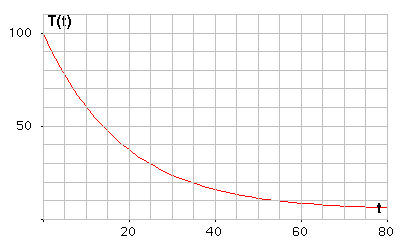
image.png
经常在「热度排名」中扮演「自然冷却」的角色。