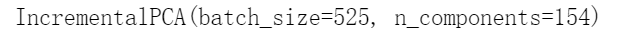许多机器学习问题涉及每个训练实例的成千上万甚至数百万个特征。正如我们将看到的那样，所有这些特征不仅使训练变得极其缓慢，而且还会使找到好的解决方案变得更加困难。这个问题通常称为维度的诅咒。
幸运的是，在实际问题中，通常可以大大减少特征的数量，从而将棘手的问题转变为易于解决的问题。例如，考虑MNIST图像(在第3章中介绍)：图像边界上的像素几乎都是白色，因此你可以从训练集中完全删除这些像素而不会丢失太多信息。图7-6确认了这些像素对于分类任务而言完全不重要。另外，两个相邻的像素通常是高度相关的，如果将它们合并为一个像素(例如，通过取两个像素的平均值)，不会丢失太多信息。

数据降维确实会丢失一些信息（就好比将图像压缩为JPEG会降低其质量一样），所以，它虽然能够加速训练，但是也会轻微降低系统性能。同时它也让流水线更为复杂，维护难度上升。因此，如果训练太慢，你首先应该尝试的还是继续使用原始数据，然后再考虑数据降维。不过在某些情况下，降低训练数据的维度可能会滤除掉一些不必要的噪声和细节，从而导致性能更好（但通常来说不会，它只会加速训练）。

除了加快训练，降维对于数据可视化（或称DataViz）也非常有用。将维度降到两个（或三个），就可以在图形上绘制出高维训练集，通过视觉来检测模式，常常可以获得一些十分重要的洞察，比如聚类。此外，DataViz对于把你的结论传达给非数据科学家至关重要，尤其是将使用你的结果的决策者。
本章将探讨维度的诅咒，简要介绍高维空间中发生的事情。然后，我们将介绍两种主要的数据降维方法（投影和流形学习），并学习现在最流行的三种数据降维技术：PCA、FA以及LLE。

8.1 维度的诅咒

我们太习惯三维空间[1]的生活，所以当我们试图去想象一个高维空间时，直觉思维很难成功。即使是一个基本的四维超立方体（见图8-1），我们也很难在脑海中想象出来，更不用说在一个千维空间中弯曲的二百维椭圆体。

事实证明，在高维空间中，许多事物的行为都迥然不同。例如，如果你在一个单位平面（1×1的正方形）内随机选择一个点，那么这个点离边界的距离小于0.001的概率只有约0.4%（也就是说，一个随机的点不大可能刚好位于某个维度的“极端”）。但是，在一个10000维的单位超立方体（1×1…×1立方体，一万个1）中，这个概率大于99.99999%。高维超立方体中大多数点都非常接近边界[3]。
还有一个更麻烦的区别：如果你在单位平面中随机挑两个点，这两个点之间的平均距离大约为0.52。如果在三维的单位立方体中随机挑两个点，两点之间的平均距离大约为0.66。但是，如果在一个100万维的超立方体中随机挑两个点呢？不管你相信与否，平均距离大约为408.25（约等于)！这是非常违背直觉的：位于同一个单位超立方体中的两个点，怎么可能距离如此之远？这个事实说明高维数据集有很大可能是非常稀疏的：大多数训练实例可能彼此之间相距很远。当然，这也意味着新的实例很可能远离任何一个训练实例，导致跟低维度相比，预测更加不可靠，因为它们基于更大的推测。简而言之，训练集的维度越高，过拟合的风险就越大。
理论上来说，通过增大训练集，使训练实例达到足够的密度，是可以解开维度的诅咒的。然而不幸的是，实践中，要达到给定密度，所需要的训练实例数量随着维度的增加呈指数式上升。仅仅100个特征下（远小于MNIST问题），要让所有训练实例（假设在所有维度上平均分布）之间的平均距离小于0.1，你需要的训练实例数量就比可观察宇宙中的原子数量还要多。
[1] 好吧，如果算上时间就是四维，或者如果你是个弦物理学家，还可以再高几个维度。
[2] 在https://homl.info/30上可以观看一个投影到三维空间的旋转超立方体。图片由维基百科用户NerdBoy1932提供（Creative Commons BY-SA 3.0），转自https://en.wikipedia.org/wiki/Tesseract。
[3] 趣味事实：只要你考虑足够多的维度，你所知道的每个人，至少在某一个维度上，都可能算是个极端主义者（比如，他们在咖啡里放多少糖）。

8.2 降维的主要方法

在深入研究特定的降维算法之前，让我们看一下减少维度的两种主要方法：投影和流形学习。

8.2.1 投影

在大多数实际问题中，训练实例并不是均匀地分布在所有维度上。许多特征几乎是恒定不变的，而其他特征则是高度相关的（如之前针对MNIST所述）。结果，所有训练实例都位于（或接近于）高维空间的低维子空间内。这听起来很抽象，所以让我们看一个示例。在图8-2中，你可以看到由圆圈表示的3D数据集。

请注意，所有训练实例都位于一个平面附近：这是高维（3D）空间的低维（2D）子空间。如果我们将每个训练实例垂直投影到该子空间上（如实例连接到平面的短线所示），我们将获得如图8-3所示的新2D数据集——我们刚刚将数据集的维度从3D减少到2D。注意，轴对应于新特征z1和z2（平面上投影的坐标）。
但是，投影并不总是降低尺寸的最佳方法。在许多情况下，子空间可能会发生扭曲和转动，例如在图8-4中所示的著名的瑞士卷小数据集中。
如图8-5左侧所示，简单地投影到一个平面上（例如，去掉x3维度）会将瑞士卷的不同层挤压在一起。你真正想要的是展开瑞士卷，得到图8-5右侧的2D数据集。

8.2.2 流形学习

瑞士卷是2D流形的一个示例。简而言之，2D流形是可以在更高维度的空间中弯曲和扭曲的2D形状。更一般而言，d维流形是n维空间（其中d许多降维算法通过对训练实例所在的流形进行建模来工作。这称为流形学习。它依赖于流形假设（也称为流形假说），该假设认为大多数现实世界的高维数据集都接近于低维流形。通常这是根据经验观察到的这种假设。
再次考虑一下MNIST数据集：所有手写数字图像都有一些相似之处。它们由连接的线组成，边界为白色，并且或多或少居中。如果你随机生成图像，那么其中只有一小部分看起来像手写数字。换句话说，如果你试图创建数字图像，可用的自由度大大低于允许你生成任何图像的自由度。这些约束倾向于将数据集压缩为低维流形。
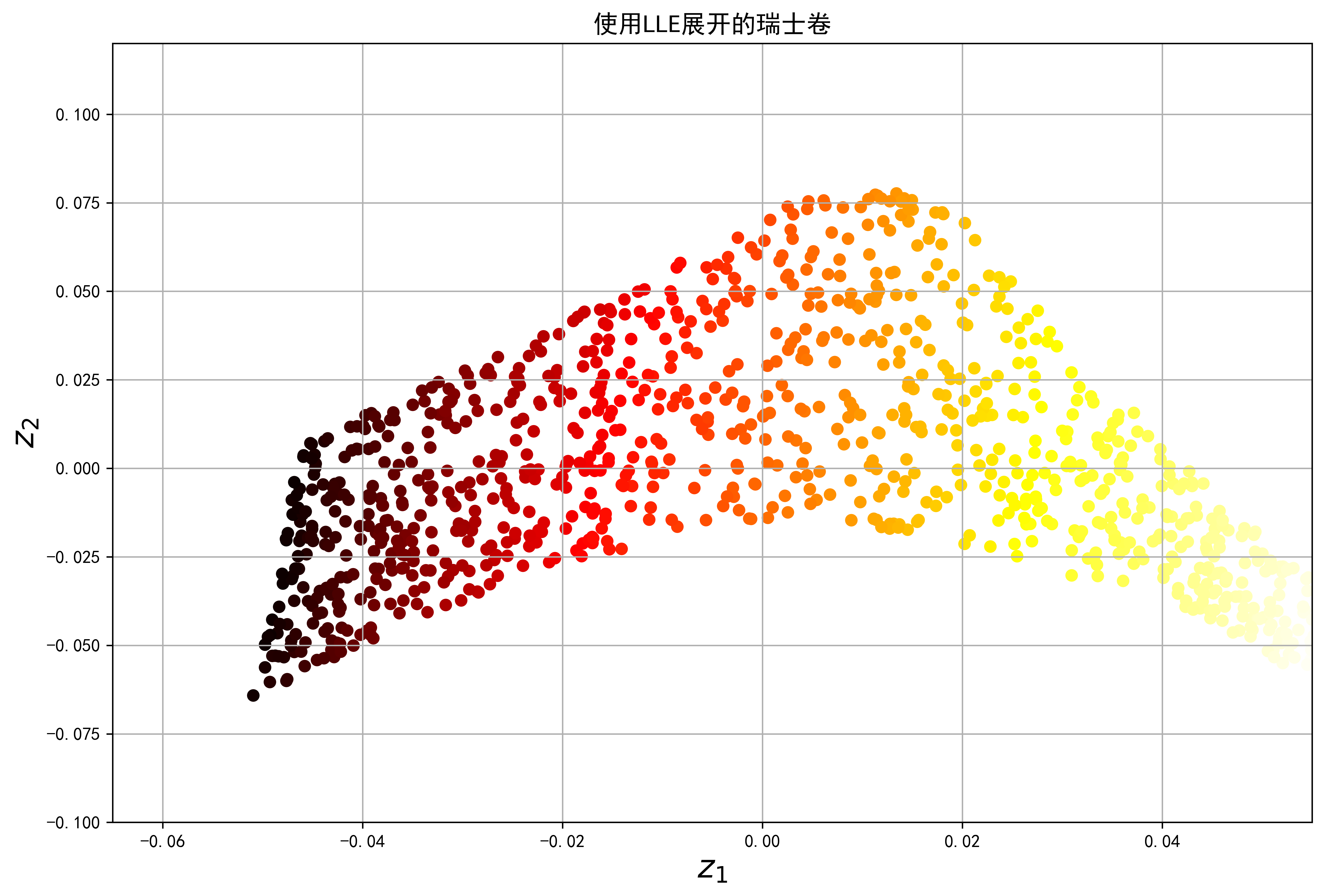
流形假设通常还伴随着另一个隐式假设：如果用流形的低维空间表示，手头的任务（例如分类或回归）将更加简单。例如，在图8-6的上面一行中，瑞士卷分为两类：在3D空间（左侧）中，决策边界会相当复杂，而在2D展开流形空间中（右侧），决策边界是一条直线。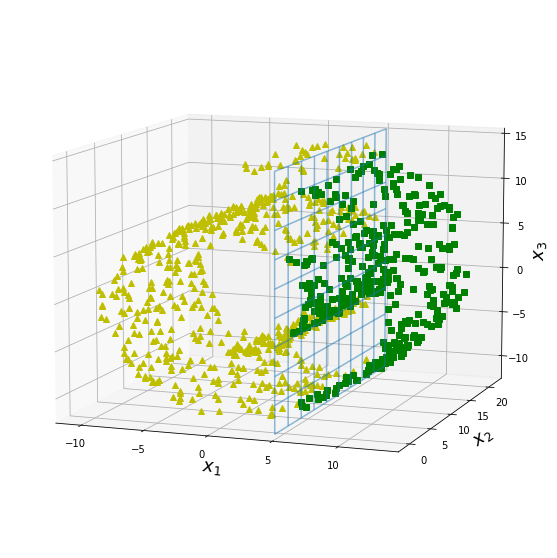

我们再来把图8-6中的瑞士卷数据降维到二维空间后的情况和原图做一下对比。

图8-6-1中蓝色网格为决策边界线，这是决策边界比较容易找到的一种情况，我们再来看另外一种不容易在3D空间中寻找到决策边界的情况。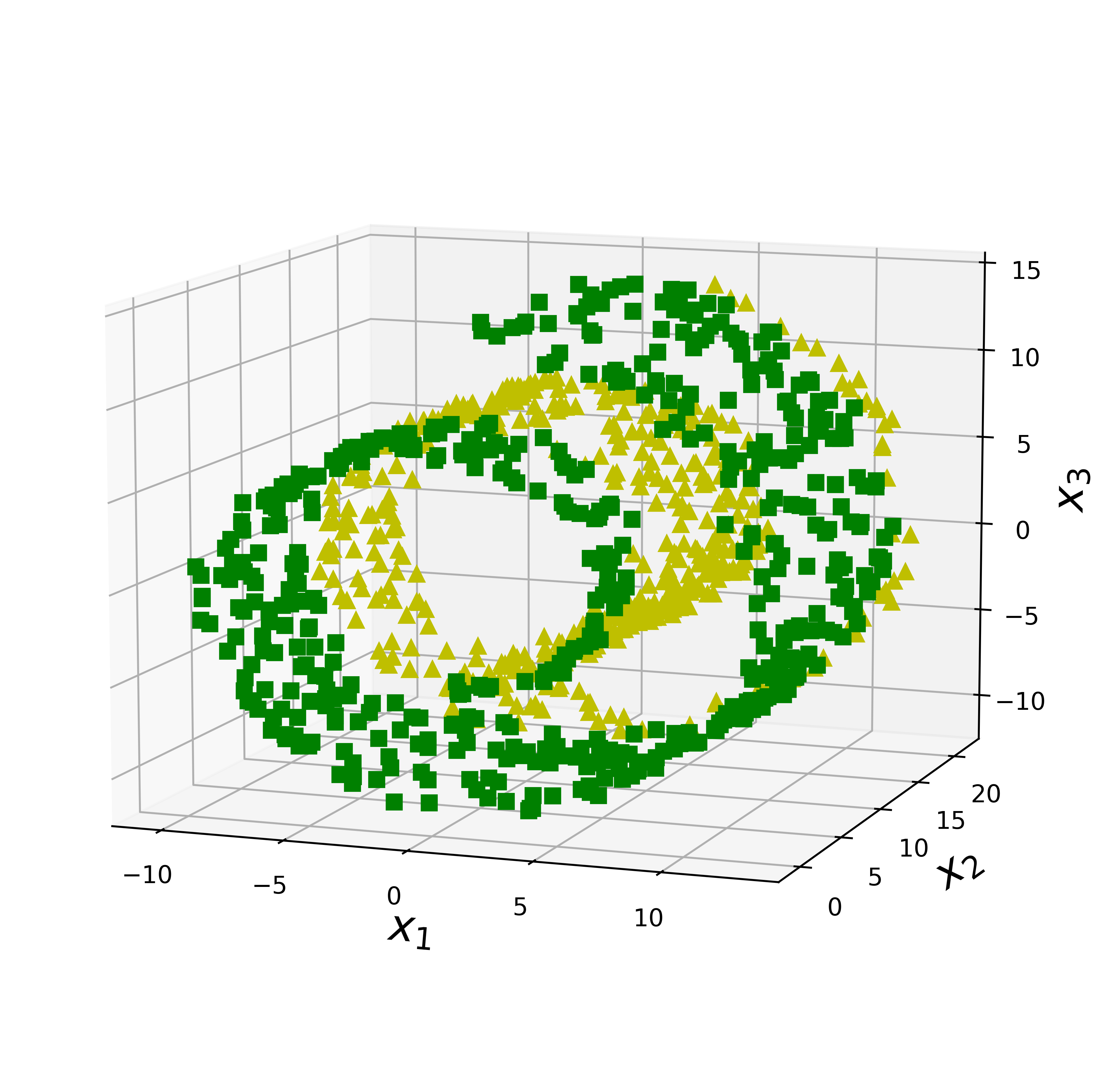

把图8-6-3中的数据降维到二维平面进行对比：

通过把两组3维空间内的瑞士卷数据降维后的对比，可以发现决策边界不总是维度越低越简单。例如，在图8-6的下面一行中，决策边界位于x1=5处。此决策边界在原始3D空间（垂直平面）中看起来非常简单，但在展开流形中看起来更加复杂（四个独立线段的集合）。
简而言之，在训练模型之前降低训练集的维度肯定可以加快训练速度，但这并不总是会导致更好或更简单的解决方案，它取决于数据集。
希望现在你对于维度的诅咒有了一个很好的理解，也知道降维算法是怎么解决它的，特别是当流形假设成立的时候应该怎么处理。本章剩余部分将逐一介绍几个最流行的算法。

8.3 PCA

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。如图8-2所示。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

8.3.1 保留差异性

将训练集投影到低维超平面之前需要选择正确的超平面。例如图8-7的左图代表一个简单的2D数据集，沿三条不同的轴（即一维超平面）。右图是将数据集映射到每条轴上的结果。正如你所见，在实线上的投影保留了最大的差异性，而点线上的投影只保留了非常小的差异性，虚线上的投影的差异性居中。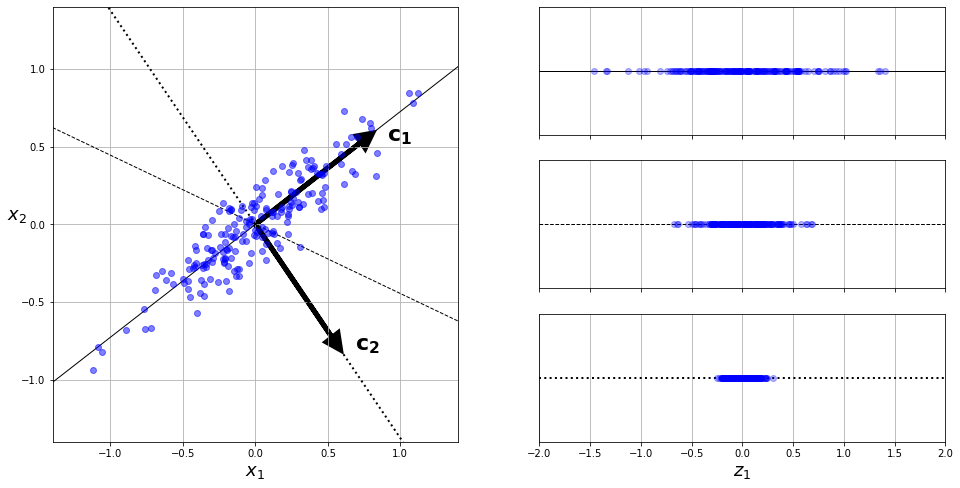

选择保留最大差异性的轴看起来比较合理，因为它可能比其他两种投影丢失的信息更少。要证明这一选择，还有一种方法，即比较原始数据集与其轴上的投影之间的均方距离，使这个均方距离最小的轴是最合理的选择，也就是实线代表的轴。这也正是PCA背后的简单思想[1]。

8.3.2协方差与协方差矩阵

那么我们如何得到这些保留了最大差异性的主成分方向呢？答案是通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值与特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。
这里引入了一个新的概念协方差矩阵，那么我们来了解一下什么是协方差矩阵并且如何用计算机帮助我们求得它。
大多数人都会有这样一种感觉，一般而言一个人如果数学成绩好，它的物理成绩大概率也会不错，反之亦然。但是数学成绩与英语成绩的却没有那么相关，至少说不像是数学成绩和物理成绩关联那样密切。
我们为了具体量化这种现象，引入协方差这个概念，对于随机变量 X 和 Y，二者的协方差定义如下：

其中，和 v 分别是 X 和 Y 的期望。而方差的定义为通过对比不难发现可以将方差看做是协方差的一种特殊形式。
通过上面协方差的定义式，我们可以用通俗的话来概况这里面的含义：

• 当 X 和 Y 的协方差为正的时候，表示当 X 增大的时候，Y 也倾向于随之增大；
• 协方差为负的时候，表示当 X 增大，Y 倾向于减小；
• 当协方差为 0 的时候，表示当 X 增大时，Y 没有明显的增大或减小的倾向，二者是相互独立的。

因此以上两变量间的相互关系分别对应为三种情况：线性正相关，线性负相关和线性不相关。也就是说如果两个变量的协方差结果为正值，则说明两者是线性正相关的；如果结果为负值，则两者是线性负相关；如果结果为0，则两者线性不相关。
我们可以引入一个协方差矩阵，将一组变量 X1、X2、X3 两两之间的协方差用矩阵的形式统一进行表达：

协方差矩阵的第 i 行、第 j 列，表示 Xi 和 Xj 之间的协方差，而对角线上表示随机变量自身的方差。我们从定义中可以看出与显然是相等的。我们总结一下协方差矩阵的特点如下：

1. 协方差矩阵是一个对称矩阵，且是半正定矩阵，主对角线是各个随机变量 的方差（各个维度上的方差）。
2. 标准差和方差一般是用来描述一维数据的；对于多维情况，而协方差是用于描述任意两维数据之间的关系，一般用协方差矩阵来表示。因此协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。
3. 协方差计算过程可简述为：先求各个分量的均值E(Xi)和E(Xj)，然后每个分量减去各自的均值得到两条向量，在进行内积运算，然后求内积后的总和，最后把总和除以n-1。

8.3.3 皮尔森相关系数

通过求两变量直接的协方差矩阵，我们可以判断数据集出不同特征两两之间的相关性，那么他们直接相关程度又该如何度量呢？你可能会有疑问协方差矩阵中的数值大小，是否能代表两个变量之间的相关度呢？实际上虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但其数值上受量纲的影响很大，不能简单地从协方差的数值大小给出变量相关程度的判断。为了消除这种量纲的影响，于是就有了皮尔森相关系数的概念。
我们先来看一下皮尔森相关系数的定义：

我们通过对比皮尔森相关系数和协方差的定义可以发现，皮尔森相关系数是由变量间的协方差除以变量间的标准差得到的。当两个变量的方差都不为零时，相关系数才有意义，相关系数的取值范围为[-1,1]。《数据挖掘导论》中给了一个很形象的图来说明相关度大小与相关系数之间的联系：

由上图可以总结，当相关系数为1时，成为完全正相关；当相关系数为-1时，成为完全负相关；相关系数的绝对值越大，相关性越强；相关系数越接近于0，相关度越弱。

8.4 PCA算法的实现

由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：

1. 基于特征值分解协方差矩阵实现PCA算法。
2. 基于SVD分解协方差矩阵实现PCA算法。

   8.4.1 基于特征值分解与协方差矩阵实现PCA算法

   零均值化处理

   我们首先回顾一下协方差的定义公式：
   
   感觉公式还不够简练，我们发现如果变量 X 和变量 Y 的均值为 0，那么协方差的式子就会变得更加简单。
   这个其实好办，我们将 X 中的每一个变量都减去它们的均值 μ，同样将 Y 中的每一个变量都减去它们的均值 v，这样经过零均值化处理后，特征 X 和特征 Y 的平均值都变为了 0。很显然，这样的处理并不会改变方差与协方差的值，因为数据的离散程度并未发生改变，同时，从公式的表达上来看也非常清楚。
   经过零均值处理后，X 和 Y 的协方差矩阵就可以写作：
   
   不难发现这个矩阵它就是零均值化后的样本矩阵。

   计算协方差矩阵

   最后，我们来实践一下协方差矩阵的求解方法，来求一下由某中学100名学生语文、历史、政治、数学、物理、化学成绩构成的协方差矩阵。
   首先读取数据，并选取数据集中的前10行数据。

   import pandas as pd
   import matplotlib.pyplot as plt
   import numpy as np
   path=r'D:\Python data\DataForClassify.csv'
   dataset=pd.read_csv(path)
   data=dataset.iloc[0:10,:]
   data

   
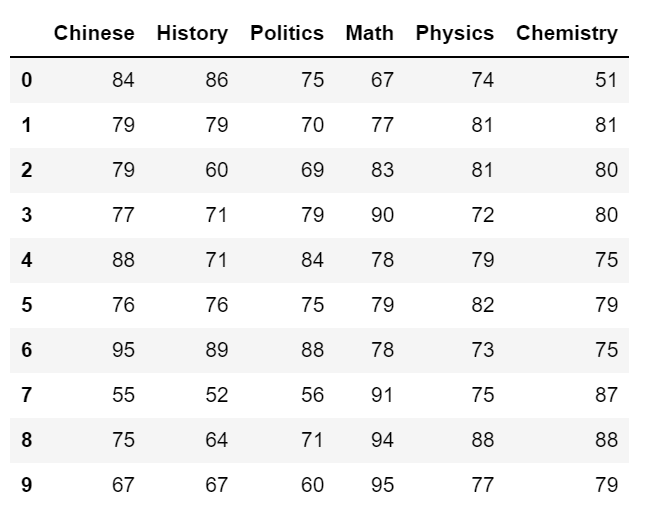
   接下来把数据形式转化为数组形式即array形式，并且把原来的int64型数据转化为float64类型

   data_array=dataset.iloc[:,2:].values
   data_array=np.array(data_array,dtype=np.float64) 
   data_array.dtype

   
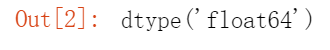
   对数据进行零均值化

   data_array -= np.mean(data_array, axis=0)
   data_array[0:10]

   
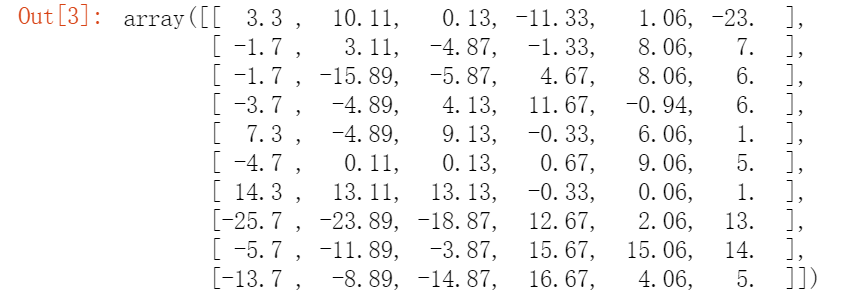
   根据协方差矩阵的计算方法即假设经过零均值化处理后的数据集为，则协方差矩阵为，其中Xi为特征值，n为样本观测数据个数。因此带入本数据集中的数据data_array后求出协方差矩阵cor_matrix为:

   cor_matrix=np.dot(data_array.T,data_array)/(100-1)
   cor_matrix=cor_matrix.round()
   cor_matrix

   
   我们也可以直接调用numpy库中的np.cor()函数直接对数据集求解协方差矩阵

   data_array_cov=np.cov(data_array,rowvar=0)
   data_array_cov=data_array_cov.round()
   data_array_cov

   
   通过观察可以发现用np.cor()求解的协方差矩阵与我们通过定义计算的结果是一致的。

   用特征值分解方法求协方差矩阵的特征值与特征向量

   关于特征值与特征向量这些线性代数方面的内容，读者请参阅机器学习数学基础中线性代数的部分，这里不再对概念做过多的介绍，只对求解过程进行适当的说明解释。
   现在我们可以调用numpy库中的linalg类中的eig()方法，直接对协方差矩阵求出特征值以及对应的特征向量。

   evalue, evector = np.linalg.eig(cor_matrix)
   print(evalue)
   print('===============================================================')
   print(evector)

   

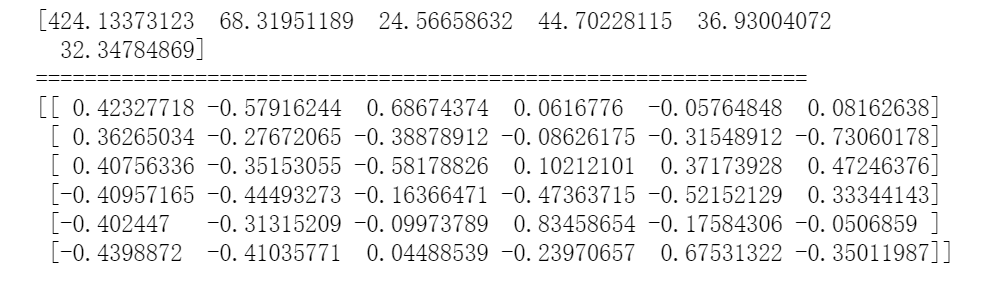
   对特征值从大到小排序，选择其中最大的k个组成特征向量矩阵P

   将特征值按照从到到小的顺序进行排序，然后再将特征值与特征向量配对。

   eig_pairs = [(np.abs(eig_value[i]), eig_vector[:,i]) for i in range(len(eig_value))]
   eig_pairs.sort(key = lambda x: x[0], reverse=True)
   print('按特征值降序排列')
   print(eig_pairs)

   
   因为我们想要通过数据集压缩到特征子空间来降低维数，所以只需选择保护最多信息（方差）的特征向量（主成分）的子集。特征值代表特征向量的大小，通过对特征值进行降序排列，我们就可以找出前K个最重要的特征向量。在对K取值之前，我们可以先把特征值的可解释方差比率求出来，特征值的可解释方差比就是特征值与特征值总和之比。
   

先求出各个主成分的可解释方差比率

tot = sum(eig_value)
var_exp = [(i / tot)*100 for i in sorted(eig_value, reverse=True)]
print('每个主成分的贡献率为：\n', var_exp)

再求出各特征值的累计贡献率。

cum_var_exp = np.cumsum(var_exp)
for i in range(len(cum_var_exp)):
    print('第{}个主成分的累积贡献率是：'.format(i), cum_var_exp[i])

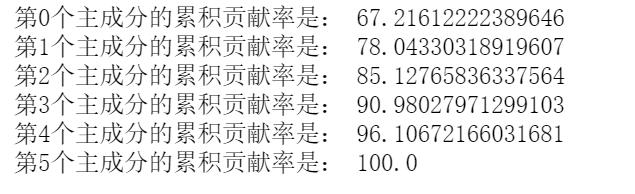
然后再把各特征值累计贡献率用台阶图的形式绘制出来。

import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties 
plt.figure(figsize=(10, 5), dpi = 600)
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc")
plt.bar(range(6), var_exp, alpha=0.5, align='center', label='第n个主成分的贡献率')
plt.step(range(6), cum_var_exp, where='mid', label='前n个主成分累计贡献率')
plt.ylabel('贡献度', FontProperties = font_set)
plt.xlabel('主成分(数量为样本数据的特征个数)', FontProperties = font_set)
plt.legend(loc = 'right', prop = font_set)
plt.show()

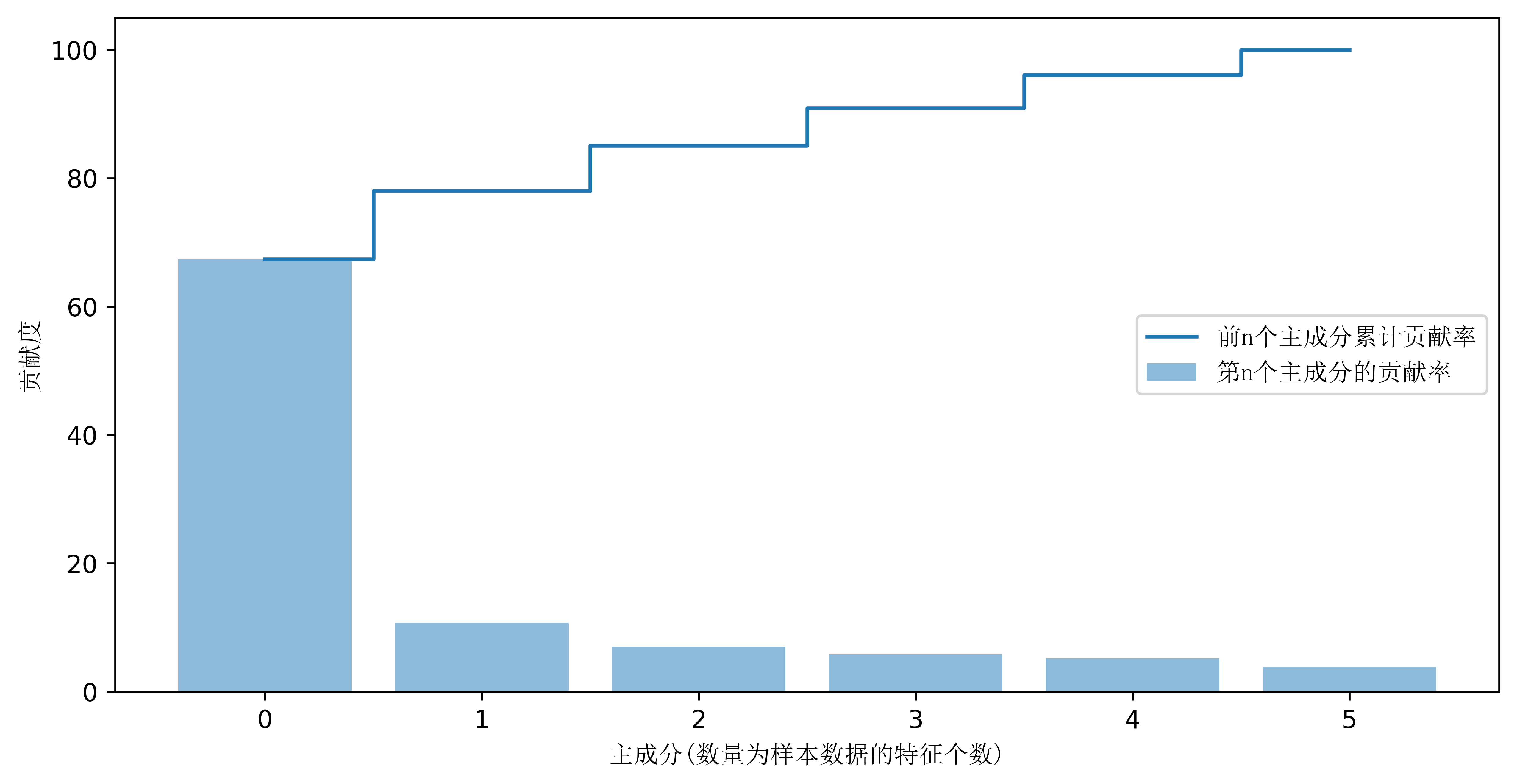
通过求出的累计贡献率可以看到前2个特征值与特征向量构成的主成分已经可以还原78%的原始数据信息。所以我们选取前K=2个特征向量构成的矩阵P。用来代表原始数据集的主要特征。

eigVector_MatrixP = np.hstack((eig_pairs[0][1].reshape(6,1),
                      eig_pairs[1][1].reshape(6,1)))
print('特征向量矩阵P:\n', eigVector_MatrixP)

将数据转换到k个特征向量构建的新空间中，即Y=PX

确定了特征向量矩阵P之后，我们将零均值化处理后的原始数据X用点积的方式乘以矩阵P，得到新的矩阵Y。这样我们可以看到通过对协方差矩阵求前K个主成分的方法，成功把原始数据集中的6维特征矩阵X投影到2维超平面Y上。从而保留了数据集大部分的差异性。最终，2维投影看起来非常类似于原始数据集。这样我们就可以在平面直角坐标系中用绘图的方法，直观地体现出降维后的数据，用来发现数据之间直接的关系。

data_array_projection = np.mat(data_array)*np.mat(eigVector_MatrixP)
data_projection=pd.DataFrame(data_array_projection)
data_projection

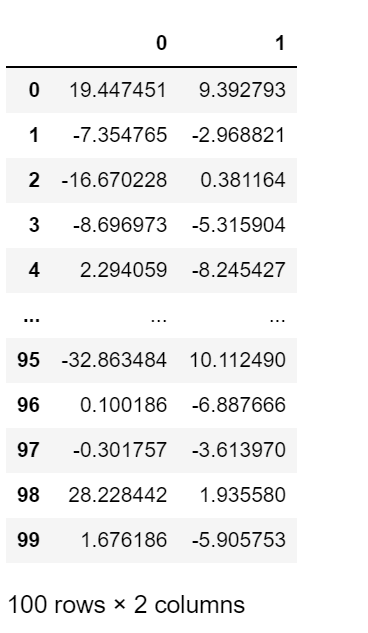
再将降维后的数据在平面直角坐标系中绘制出来。

train_y=dataset.iloc[:,1].values
ClassifyResult=pd.DataFrame(train_y)
plt.rcParams['axes.unicode_minus'] = False 
plt.figure(dpi = 600)
plt.scatter(data_projection.iloc[:, 0], data_projection.iloc[:, 1],c=ClassifyResult.iloc[:,0])
plt.show()

至此我们已经将原始数据中100个6维特征数据降维到了二维平面之内。通过观察图像，我们可以把原始数据集分为3大类别。到这里我们用对协方差矩阵特征值分解对高维数据进行降维就全部完成了。

在PCA降维中，我们需要找到样本协方差矩阵[1] 的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵,当样本数多、样本特征数也多的时候，这个计算还是很大的。这时我们就有必要用另外一种方法对协方差矩阵进行分解了。
[1] 这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

8.4.2 基于SVD分解协方差矩阵实现PCA算法

上一节中我们在用特征值和特征向量对原始数据进行降维时，如果我们不进行协方差矩阵 X 的求取，绕开它直接对原始的数据采样矩阵 A 进行矩阵分解，从而进行降维操作，行不行？
如果继续沿用上面的办法，显然是不行的，特征值分解对矩阵的要求很严，首先得是一个方阵，其次在方阵的基础上，还得满足可对角化的要求。但是原始的 m×n数据采样矩阵 A 连方阵这个最基本的条件都不满足，是根本无法进行特征值分解的。

SVD奇异值分解

幸运的是，有一种称为奇异值分解（SVD）的标准矩阵分解技术，该技术可以将训练集矩阵X分解为三个矩阵UΣVT的矩阵乘法，其中V包含定义所有主要成分的单位向量。如公式8-1所示。

什么是奇异值？首先给大家介绍一个对于任意 m×n 矩阵的更具普遍意义的一般性质：

对于一个 m×n秩为 r 的矩阵 A，这里我们暂且假设 m>n，于是就有 r≤n<m 的不等关系。我们在Rn空间中一定可以找到一组标准正交向量在 Rm空间中一定可以找到另一组标准正交向量使之满足 n 组相等关系：，其中（i 取 1~n）。

，这个等式非常神奇，我们仔细地揭开里面的迷雾，展现它的精彩之处。矩阵 A 是一个 m×n的矩阵，它所表示的线性变换是将 n 维原空间中的向量映射到更高维的 m 维目标空间中，而这个等式意味着，在原空间中找到一组新的标准正交向量，在目标空间中存在着对应的一组标准正交向量并且，此时 vi 与 ui线性无关。
当矩阵 A 作用在原空间上的某个基向量 vi上时，其线性变换的结果就是：对应在目标空间中的
ui向量沿着自身方向伸长 σi倍，并且任意一对 (vi,ui)向量都满足这种关系（显然特征值分解是这里的一种特殊情况，即两组标准正交基向量相等）。如图 8-4-2 所示：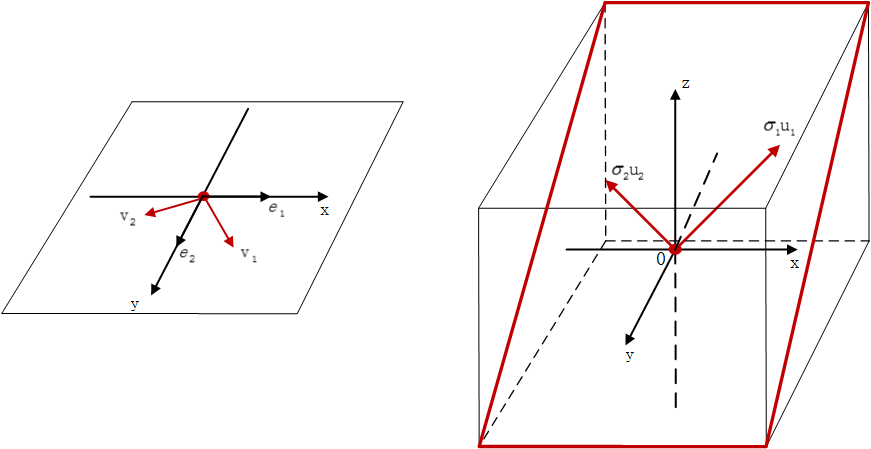

在基础上，我们继续往前走。可以得到：

此时感觉还差一点，因为我们发现 并没有包含在式子里，我们把它们加进去，把加到矩阵右侧，形成完整的 m 阶方阵：

在对角矩阵下方加上 m-n 个全零行，形成 m×n 的矩阵：

很明显由于矩阵最下面的 m-n 行全零，因此右侧的计算结果不变，等式依然成立。此时就有由于 V 的各列是标准正交向量，因此，移到等式右侧，得到了一个矩阵分解的式子：

注意该公式中：U为m阶方阵，VT为n阶方阵，而Σ为是一个 m×n的对角矩阵（不是方阵）。

但是此时还有一个最关键的地方似乎没有明确：就是方阵 U 和方阵 V 该如何取得，以及 Σ矩阵中的各个值应该为多少。此时我们就需要引入格拉姆矩阵，并利用矩阵的性质来求解了首先，获取转置矩阵我们在此基础上可以获取两个对称矩阵：


我们可以得到以下性质：
ATA 是 n 阶对称方阵，AAT 是 m 阶对称方阵。它们的秩相等，为 r=Rank(A)。因此它们拥有完全相同的 r 个非零特征值，从大到小排列为 λ1,λ2,…λr
Σ矩阵中对角线上的非零值 σi从大到小依次排列则为：。因此，Σ矩阵对角线上 σr以后的元素均为 0 了。
我们隐去零特征值，最终得到了最完美的 SVD 分解结果(注意其中r≤n
我们用一个抽象图来示意一下分解的结果，有助于大家加深印象。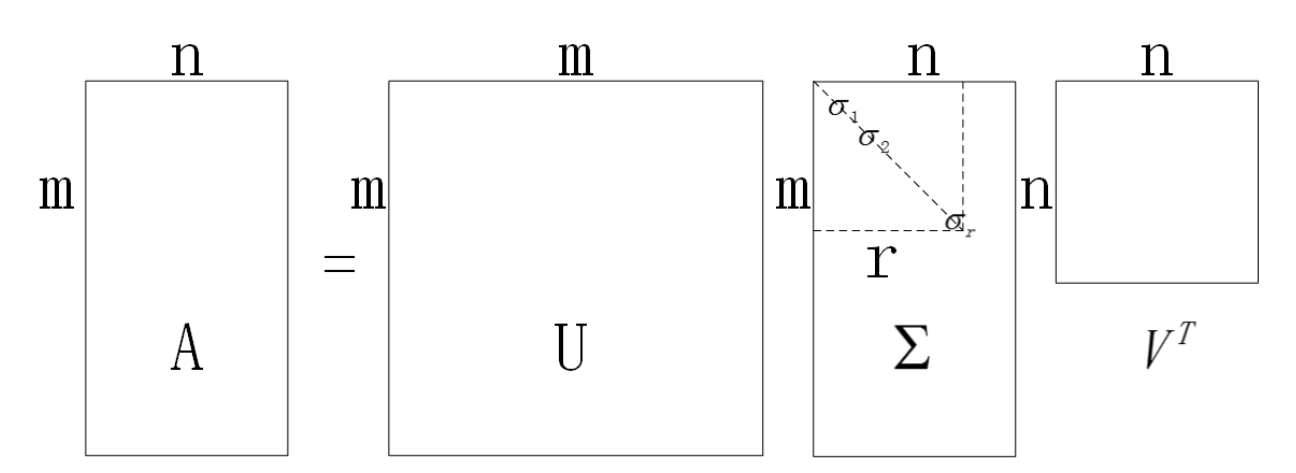

至此我们已经求得任意的m×n 矩阵A进行了SVD分解，并且得到了特征值从大到小排列的 Σ矩阵，同基于特征值分解的协方差矩阵降维方法一样，选择其中最大的k个特征值。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。我们下面看看如何用NumPy的svd（）函数来获取训练集的所有主要成分 。

U, sigma, Vt = np.linalg.svd(data_array)
print('U=',U)
print('sigma=',sigma)
print('Vt=',Vt)

接下来要求得将训练集投影到超平面上并得到维度为d的简化数据集Ad-proj，只需计算训练集矩阵A与矩阵Wk的矩阵相乘，矩阵Wk定义为包含V的前k列的矩阵，

使用Scikit-Learn

Scikit-Learn的PCA类使用SVD分解来实现PCA。以下代码应用PCA将数据集的维度降到二维（请注意，它会自动进行零均值化处理，来解决数据中心化的问题）：

from sklearn.decomposition import PCA
pca = PCA( n_components=2 )
X2D = pca.fit_transform(X)

将PCA转换器拟合到数据集后，其components属性是Wk的转置（例如，定义第一个
主成分的单位向量等于pca.components.T[：，0]）。

可解释方差比

另一个有用的信息是每个主成分的可解释方差比，可以通过explainedvariance_ratio变量来获得。该比率表示沿每个成分的数据集方差的比率。例如，让我们看一下图8-2中表示的3D数据集的前两个成分的可解释方差比：

pca.explained_variance_ratio_

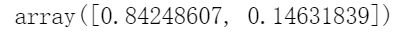
此输出告诉你，数据集方差的84.2%位于第一个PC上，而14.6%位于第二个PC上。对于第三个PC，这还不到1.2%，因此可以合理地假设第三个PC携带的信息很少。

选择正确的维度

与其任意选择要减小到的维度，不如选择相加足够大的方差部分（例如95%）的维度。当然，如果你是为了数据可视化而降低维度，这种情况下，需要将维度降低到2或3。
先引入MNIST数据集

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
mnist.target = mnist.target.astype(np.uint8)

使用Sklearn包中的train_test_split()函数划分训练集与测试集

from sklearn.model_selection import train_test_split
X = mnist["data"]
y = mnist["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y)

以下代码在不降低维度的情况下执行PCA，然后计算保留95%训练集方差所需的最小维度：

pca = PCA() pca.fit(X_train) 
cumsum = np.cumsum(pca.explained_variance_ratio_) 
d = np.argmax(cumsum >= 0.95) + 1
d

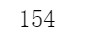
然后，你可以设置n_components=d并再次运行PCA。但是还有一个更好的选择：将 n_components设置为0.0到1.0之间的浮点数来表示要保留的方差率，而不是指定要保留的主成分数：

pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X_train)

另一个选择是将可解释方差绘制成维度的函数（简单地用cumsum绘制，见图8-8）。曲线上通常会出现一个拐点，其中可解释方差会停止快速增大。在这种情况下，你可以看到将维度降低到大约150而不会损失太多的可解释方差。

plt.figure(figsize=(12,8),dpi=600)
plt.rc('font',family='SimHei')
plt.plot(cumsum, linewidth=3)
plt.axis([0, 400, 0, 1])
plt.xlabel("维度")
plt.ylabel("可解释方差")
plt.plot([d, d], [0, 0.95], "k:")
plt.plot([0, d], [0.95, 0.95], "k:")
plt.plot(d, 0.95, "ko")
plt.annotate("拐点", xy=(65, 0.85), xytext=(70, 0.7),
             arrowprops=dict(arrowstyle="->"), fontsize=16)
plt.grid(True)
plt.show()

8.4.3 PCA压缩

降维后，训练集占用的空间要少得多。例如，将PCA应用于MNIST数据集，同时保留其95%的方差。你会发现每个实例将具有150多个特征，而不是原始的784个特征。因此，尽管保留了大多数方差，但数据集现在不到其原始大小的20%！这是一个合理的压缩率，你可以看到这种维度减小极大地加速了分类算法（例如SVM分类器）。
通过应用PCA投影的逆变换，还可以将缩减后的数据集解压缩回784维。由于投影会丢失一些信息（在5%的方差被丢弃），因此这不会给你原始的数据，但可能会接近原始数据。原始数据与重构数据（压缩后再解压缩）之间的均方距离称为重构误差。
以下代码将MNIST数据集压缩为154个维度，然后使用inverse_transform（）方法将其解压缩回784个维度：

pca = PCA(n_components=154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)

图8-9显示了原始训练集的一些数字（左侧），以及压缩和解压缩后的相应数字。你会看到图像质量略有下降，但是数字仍然大部分保持完好。

8.4.4 随机PCA

如果将超参数svd_solver设置为”randomized”，则Scikit-Learn将使用一种称为Randomized PCA的随机算法，该算法可以快速找到前d个主成分的近似值。它的计算复杂度为O(m×d2)+O(d3)，而不是完全SVD方法的O(m×n2)+O(n3)，因此，当d远远小于n时，它比完全的SVD快得多：

rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)

默认情况下，svd_solver实际上设置为”auto”：如果m或n大于500并且d小于m或n的80%，则Scikit-Learn自动使用随机PCA算法，否则它将使用完全的SVD方法。如果要强制Scikit-Learn使用完全的SVD，可以将svd_solver超参数设置为”full”。

8.4.5 增量PCA

前面的PCA实现的一个问题是，它们要求整个训练集都放入内存才能运行算法。幸运的是已经开发了增量PCA（IPCA）算法，它们可以使你把训练集划分为多个小批量，并一次将一个小批量送入IPCA算法。这对于大型训练集和在线（即在新实例到来时动态运行）应用PCA很有用。
以下代码将MNIST数据集拆分为100个小批量（使用NumPy的array_split（）函数），并将其馈送到Scikit-Learn的IncrementalPCA类[2]，来把MNIST数据集的维度降低到154（就像之前做的那样）。请注意，你必须在每个小批量中调用partial_fit（）方法，而不是在整个训练集中调用fit（）方法：

from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
    print(".", end="") 
    inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)

另外，你可以使用NumPy的memmap类，该类使你可以将存储在磁盘上的二进制文件中的大型数组当作完全是在内存中一样来操作，该类仅在需要时才将数据加载到内存中。由于IncrementalPCA类在任何给定时间仅使用数组的一小部分，因此内存使用情况处于受控状态。如以下代码所示，这使得调用通常的fit（）方法成为可能：

filename = "my_mnist.data"
m, n = X_train.shape
X_mm = np.memmap(filename, dtype='float32', mode='write', shape=(m, n))
X_mm[:] = X_train
del X_mm
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)

8.5 FA(Factor analysis)因子分析

1904年，英国心理学家CharlesSpearman研究了33名学生在古典语、法语和英语三门成绩，三门成绩的相关性系数如下：

三门成绩的高度相关会不会是由于它们三个成绩的背后有一个共同的因素，来决定这三门成绩的？比如语言能力？智力高低？对于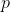个原始变量来说，那些高度相关的变量很可能会遵循一个共同的潜在结构——或可称之为公共因子 (Common factor） 。简单的说就是：公共因子是用一个共同的因素来刻画几个高度相关的变量。
然而，这些“公共因子”通常是无法观测的，故称为潜变量 (latentvariables)。这在心理学、社会学及行为科学等学科中非常常见，比如“智力”和“社会阶层”。
因子分析（Factor analysis）旨在提出因子模型（Factor model）来研究如何用几个公共因子，记作通常m＜p，来刻画原始变量之间的相关性。

8.5.1 正交因子模型

Charles Spearman基于学生3门语言成绩的数据提出了单因子模型（Single factor model）：

其中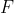代表公共因子（Common factor）;代表特殊因子（Specific factor）;即代表的特殊部分；代表系数/载荷（Loading），即来说明公共因子对的解释能力。当然，大多数时候一个公共因子是不够的，错综复杂的变量可能需要多个公共因子刻画，这就是我们将要学习的正交因子模型（Orthogonal factor model）。
假设可观测随机向量的均值为方差为。正交因子模型假定Y线性依赖于m个不可观测公共因子和p个不可观测的特殊因子 (specific factors)，通常m＜p。

使用矩阵记号，上述模型可写为：

我们知道公共因子是虚拟的，不可观测的，所以理论上，我们可以给其任意的假设，为了分析方便，我们给它一种最简单的假设，其中F和假设满足：



有了以上这些假设，我们可以计算原始变量y和公共因子f的协方差矩阵：

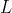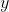综上，我们得到结论：即刻画的是和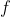之间的协方差，因此载荷测度了第个变量与第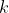个公共因子之间的关联
最终我们可以得到原始变量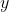的协方差矩阵:

8.5.2 因子分析的计算过程

应用因子分析算法时，常常有如下几个基本步骤：

1. 确定原有若干变量是否适合于因子分析；因子分析的基本逻辑是从原始变量中构造出少数几个具有代表意义的因子变量，这就要求原有变量之间要具有比较强的相关性，否则，因子分析将无法提取变量间的“共性特征”（变量间没有共性还如何提取共性？）。实际应用时，可以使用相关性矩阵进行验证，如果相关系数小于0.3，那么变量间的共性较小，不适合使用因子分析；也可以用KMO 和 Bartlett 的检验来判断是否适合做因子分析，一般来说KMO的值越接近于1越好，大于0.5的话适合做因子分析，你的KMO值是0.674大于0.5。Bartlett 的检验主要看Sig.越小越好，你的Sig接近于0.由此可以得出，你的数据适合做因子分析。
2. 构造因子变量；因子分析中有多种确定因子变量的方法，如基于主成分模型的主成分分析法和基于因子分析模型的主轴因子法、极大似然法、最小二乘法等。
3. 利用旋转使得因子变量更具有可解释性 ；在实际分析工作中，主要是因子分析得到因子和原变量的关系，从而对新的因子能够进行命名和解释，否则其不具有可解释性的前提下对比PCA就没有明显的可解释价值。
4. 计算因子变量的得分 。子变量确定以后，对每一样本数据，希望得到它们在不同因子上的具体数据值，这些数值就是因子得分，它和原变量的得分相对应。

具体而言：
(1) 相关性检验，一般采用KMO检验法和Bartlett球形检验法两种方法来对原始变量进行相关性检验；
(2) 输入原始数据Xn*p，计算样本均值和方差，对数据样本进行标准化处理；
(3) 计算样本的相关系数矩阵R；
(4) 求相关矩阵R的特征值和特征向量；
(5) 根据系统要求的累积贡献率确定公共因子的个数m；
(6) 计算因子载荷矩阵Loading_Matrix；
(7) 对载荷矩阵进行旋转，以求能更好地解释公共因子；
(8) 确定因子模型；
(9) 根据上述计算结果，求因子得分，对系统进行分析.
下面我们通过一个例子看一下如何用FA因子分析的方法对数据进行降维，我们还是拿某中学100名学生的6科考试成绩举例。
首先读取原始数据：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
path=r'D:\Python data\Case008_基于主成分分析(PCA)与因子分析(FA)的数据降维任务_数据\DataForClassify.csv'
dataset=pd.read_csv(path)
train_data=dataset.iloc[:,2:]
ClassifyResult=dataset.iloc[:,1].values
train_data.head(10)

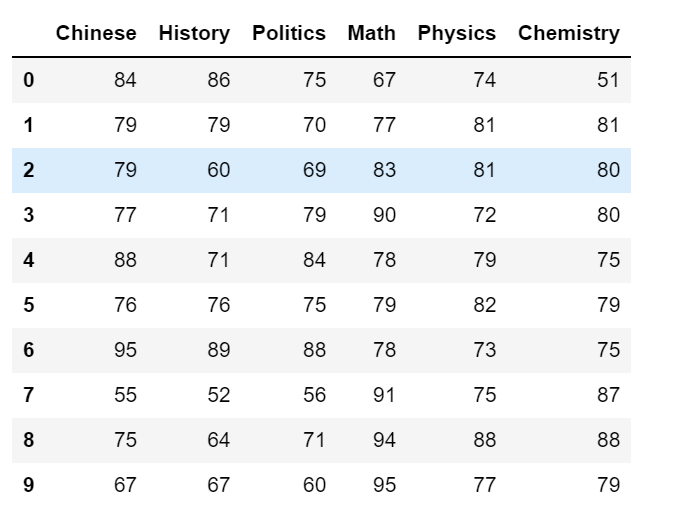
通过观察数据我们发现所有样本的数值范围都在0-100之内，这也意味着样本数据有相同的量纲，因此我们此处就不对原始数据进行归一化处理。接下来我们对6科成绩求出皮尔森系数相关矩阵。

data_corr=train_data.corr()
data_corr

我们把相关系数用热力图绘制出来。

import seaborn as sns
plt.figure(figsize=(12,10),dpi=600)
plt.rcParams['axes.unicode_minus'] = False 
sns.heatmap(data=data_corr,cmap='Blues')

通过观察相关系数热力图，我们可以明显发现数学、物理、化学三科成绩相关性很高。并且政治、历史、语文三科成绩相关性也非常高。
我们再用KMO测度和bartlett巴特利特球形检验对变量进行相关性检验。

import pandas as pd
import numpy as np
import math as math
import numpy as np
from numpy import *
from scipy.stats import bartlett
from factor_analyzer import FactorAnalyzer
import numpy.linalg as nlg
from sklearn.cluster import KMeans
from matplotlib import cm
import matplotlib.pyplot as plt

# KMO测度
def kmo(dataset_corr):
    corr_inv = np.linalg.inv(dataset_corr)
    nrow_inv_corr, ncol_inv_corr = dataset_corr.shape
    A = np.ones((nrow_inv_corr, ncol_inv_corr))
    for i in range(0, nrow_inv_corr, 1):
        for j in range(i, ncol_inv_corr, 1):
            A[i, j] = -(corr_inv[i, j]) / (math.sqrt(corr_inv[i, i] * corr_inv[j, j]))
            A[j, i] = A[i, j]
    dataset_corr = np.asarray(dataset_corr)
    kmo_num = np.sum(np.square(dataset_corr)) - np.sum(np.square(np.diagonal(A)))
    kmo_denom = kmo_num + np.sum(np.square(A)) - np.sum(np.square(np.diagonal(A)))
    kmo_value = kmo_num / kmo_denom
    return kmo_value
print("\nKMO测度:", kmo(data_corr.values))

# 巴特利特球形检验
df2_corr1 = data_corr.values
print("\n巴特利特球形检验:", bartlett(df2_corr1[0], df2_corr1[1], df2_corr1[2], df2_corr1[3], df2_corr1[4],
                                  df2_corr1[5]))

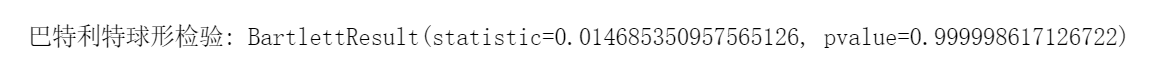
KMO大于0.5而且bartlett接近于1，完美通过检验。接下来就可以对相关系数矩阵求特征值和特征向量了。

eig_value, eig_vector = np.linalg.eig(data_corr.values)
print(eig_value)
print('===============================================================')
print(eig_vector)

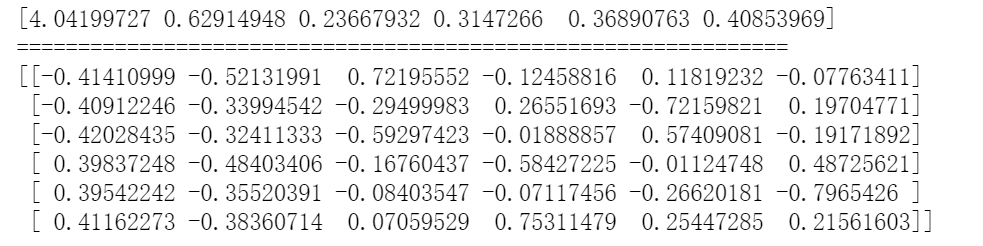
和PCA方法中求前K个特征值对应特征向量的累计贡献度类似，但区别是，PCA中单个主成分的贡献度含义为可解释方差比率，而在FA中则是单个公因子占总公共因子矩阵的百分比。

tot = sum(eig_value)
var_exp = [(i / tot)*100 for i in sorted(eig_value, reverse=True)]
print('每个公因子的贡献率为：\n', var_exp)

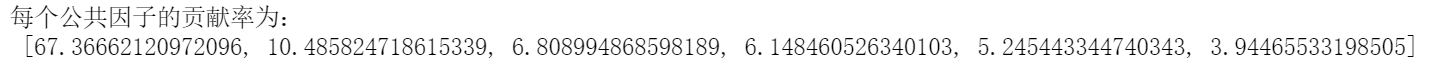
cum_var_exp = np.cumsum(var_exp)
for i in range(len(cum_var_exp)):
    print('第{}个公因子的累积贡献率是：'.format(i), cum_var_exp[i])

根据累计贡献度，选取m=2个公共因子。

Loading_Matrix=np.sqrt(eig_value)*np.array(eig_vector) #主成分乘上权重，λ的开平方，注意：此时eig_vector中一列是代表着一个特征向量
Loading_Matrix

基于相关系数矩阵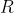的主成分法得到的载荷矩阵估计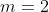（）、共同度(每个因子对公共因子的依赖程度)及特殊因子方差如下：

L_=pd.DataFrame(Loading_Matrix[:,:2],columns=['lj1','lj2'],index=[train_data.columns])
L_['共同度']=(Loading_Matrix[:,:2]*Loading_Matrix[:,:2]).sum(axis=1)
L_['特殊因子方差']=1-L_['共同度']
L_

由和可知这两个公共因子是如何决定原始变量的，如,
原始变量在两个公共因子的表现（权重）基本都不低，这样就导致一个问题：公共因子的可解释性很差。接下来我们会介绍一种方法——因子旋转，来解决此类问题。

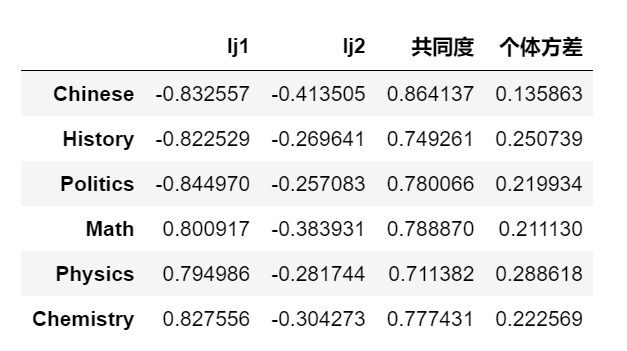
from numpy import eye, asarray, dot, sum, diag
from numpy.linalg import svd
def varimax(Phi, gamma = 1.0, q =20, tol = 1e-6):
    p,k = Phi.shape
    R = eye(k)
    d = 0
    for i in range(q):
        d_old = d
        Lambda = dot(Phi, R)
        u,s,vh = svd(dot(Phi.T,asarray(Lambda)**3 - (gamma/p) * dot(Lambda, diag(diag(dot(Lambda.T,Lambda)))))) #奇异值分解svd
        R = dot(u,vh)
        d = sum(s)
        if d_old!=0 and d/d_old < 1 + tol: break
    return dot(Phi, R)
A2 = varimax(L_.iloc[:,:2])
A2 = pd.DataFrame(A2)
A2

这样我们就可以得到旋转后的载荷矩阵A2了。对比旋转之前的载荷矩阵A，A2可以在两个维度上对因子变量进行更好的解释。最后我们用旋转后得到的载荷矩阵，对原始数据降维并绘制散点图。

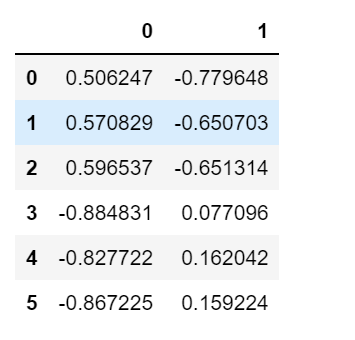
FA_Matrix=np.mat(train_data)*np.mat(A2)
test_x=pd.DataFrame(FA_Matrix)
test_x

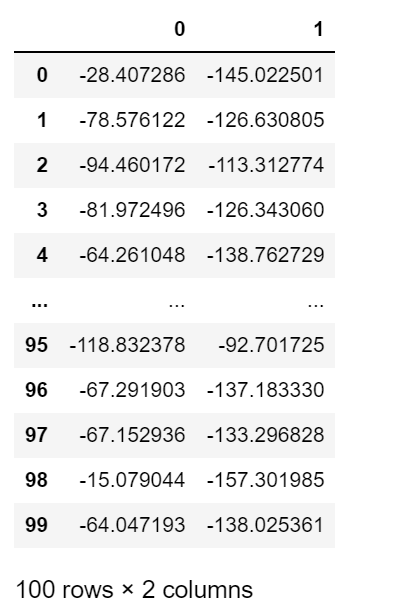
plt.figure(dpi = 600)
plt.scatter(test_x.iloc[:, 0], test_x.iloc[:, 1], c=ClassifyResult)
plt.show()

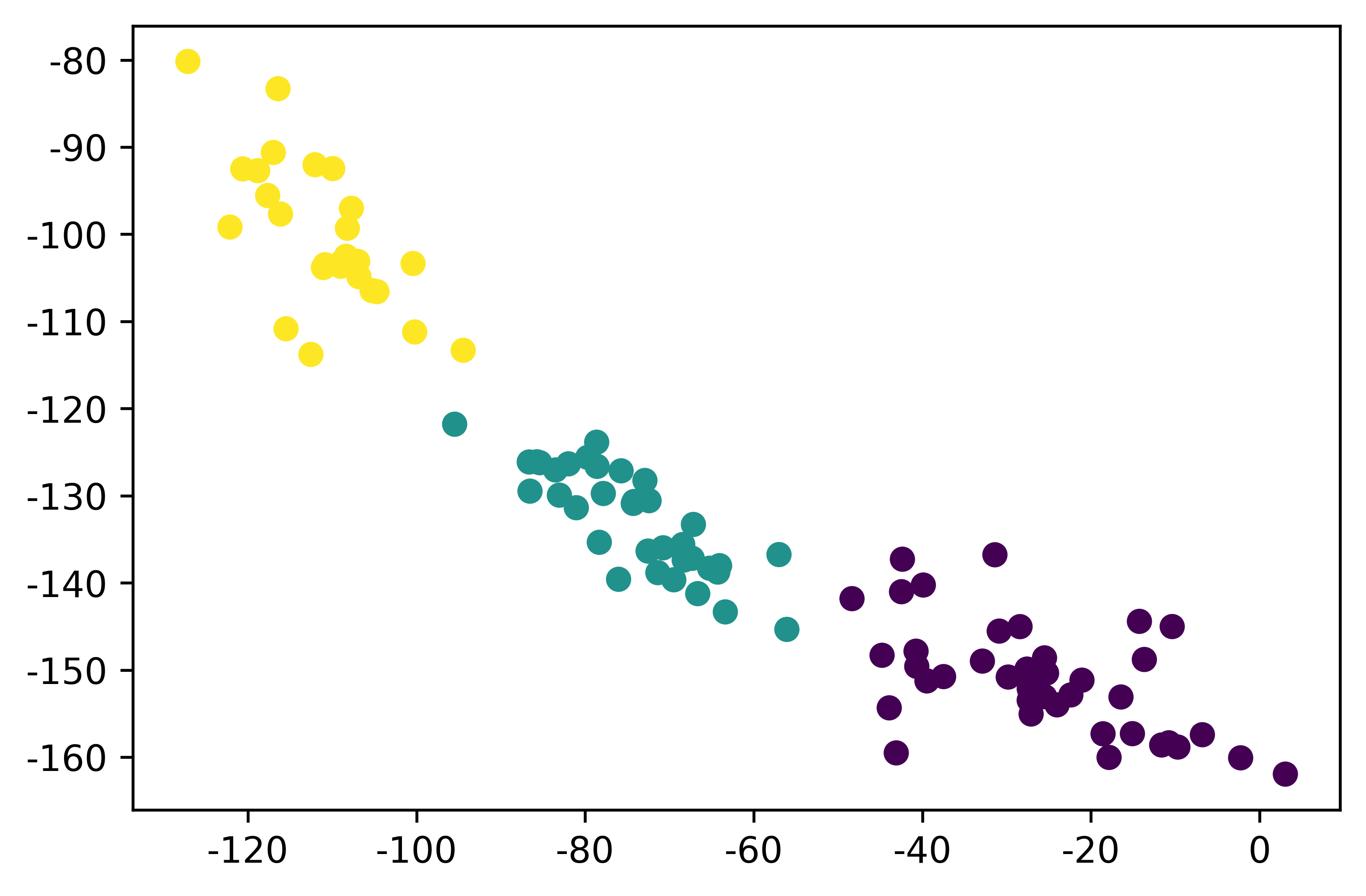
我们可以发现相交于PCA，FA可以从两个维度上都可以很好的把数据进行分类。这也是FA相当于PCA的一个优势。

8.5.3 PCA与FA的联系与区别

无论是PCA还是FA都可以对高维数据进行降维，那么二者之间有什么联系和区别呢？让我们一起来总结一下。
联系：
1. PCA和因子分析都是数据降维的重要方法，都对原始数据进行标准化处理，都消除了原始指标的相关性对综合评价所造成的信息重复的影响，都属于因素分析法，都基于统计分析法；
2. 二者均应用于高斯分布的数据，非高斯分布的数据采用ICA算法；
3. 二者构造综合评价时所涉及的权数具有客观性，在原始信息损失不大的前提下，减少了后期数据挖掘和分析的工作量。
区别：
1. 原理不同； PCA的基本原理是利用降维（线性变换)的思想，在损失很少信息的前提下把多个指标转化为几个不相关的主成分，每个主成分都是原始变量的线性组合；
而FA基本原理是从原始变量相关矩阵内部的依赖关系出发，把因子表达成能表示成少数公共因子和仅对某一个变量有作用的特殊因子的线性组合（因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系）；
2.假设条件不同； 主成分分析不需要有假设，而因子分析需要假设各个共同因子之间不相关，特殊因子（specificfactor）之间也不相关，共同因子和特殊因子之间也不相关；
3. 求解方法不同； 主成分分析的求解方法从协方差阵出发，而因子分析的求解方法包括主成分法、主轴因子法、极大似然法、最小二乘法、a因子提取法等；
4. 降维后的“维度”数量不同，即因子数量和主成分的数量； 主成分分析的数量最多等于维度数；而因子分析中的因子个数需要分析者指定（SPSS和SAS根据一定的条件自动设定，只要是特征值大于1的因子主可进入分析），指定的因子数量不同而结果也不同。
5. 线性表示方法不同； 因子分析是把变量表示成各公因子的线性组合；主成分分析中则是把主成分表示成各变量的线性组合。
6. 主成分和因子的变化不同； 主成分分析：当给定的协方差矩阵或者相关矩阵的特征值唯一时，主成分一般是固定的独特的；因子分析：因子不是固定的，可以旋转得到不同的因子。
7.解释重点不同； 主成分分析：重点在于解释个变量的总方差；因子分析：则把重点放在解释各变量之间的协方差。
8.算法上的不同； 主成分分析：协方差矩阵的对角元素是变量的方差；因子分析：所采用的协方差矩阵的对角元素不在是变量的方差，而是和变量对应的共同度（变量方差中被各因子所解释的部分）。
9.优点不同； 对于因子分析，可以使用旋转技术，使得因子更好的得到解释，因此在解释主成分方面因子分析更占优势；其次因子分析不是对原有变量的取舍，而是根据原始变量的信息进行重新组合，找出影响变量的共同因子，化简数据；如果仅仅想把现有的变量变成少数几个新的变量（新的变量几乎带有原来所有变量的信息）来进入后续的分析，则可以使用主成分分析，不过一般情况下也可以使用因子分析。

8.6 核PCA

在第5章中，我们讨论了内核，这是一种数学技术，它可以将实例隐式映射到一个高维空间（称为特征空间），从而可以使用支持向量机来进行非线性分类和回归。回想一下，高维特征空间中的线性决策边界对应于原始空间中的复杂非线性决策边界。
事实证明，可以将相同的技术应用于PCA，从而可以执行复杂的非线性投影来降低维度。这叫作内核PCA（kPCA）[1]。它通常擅长在投影后保留实例的聚类，有时甚至可以展开位于扭曲流形附近的数据集。
下面的代码使用Scikit-Learn的KernelPCA类以及用RBF内核来执行kPCA（有关RBF内核和其他内核的更多详细信息，请参见第5章）：

from sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

图8-10显示了瑞士卷，它使用线性内核（相当于简单地使用PCA类）、RBF内核和sigmoid内核减小为二维。

from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)
y = t > 6.9
plt.figure(figsize=(12,4),dpi=600)
plt.rc('font',family='SimHei')
plt.rcParams['axes.unicode_minus'] = False 
for subplot, pca, title in ((131, lin_pca, "线性内核"), (132, rbf_pca, "RBF内核, $\gamma=0.04$"), (133, sig_pca, "Sigmoid内核, $\gamma=10^{-3}, r=1$")):
    X_reduced = pca.fit_transform(X)
    if subplot == 132:
        X_reduced_rbf = X_reduced
    plt.subplot(subplot)
    #plt.plot(X_reduced[y, 0], X_reduced[y, 1], "gs")
    #plt.plot(X_reduced[~y, 0], X_reduced[~y, 1], "y^")
    plt.title(title, fontsize=14)
    plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
    plt.xlabel("$z_1$", fontsize=18)
    if subplot == 131:
        plt.ylabel("$z_2$", fontsize=18, rotation=0)
    plt.grid(True)
plt.show()

选择内核并调整超参数

由于kPCA是一种无监督学习算法，因此没有明显的性能指标可以帮助你选择最好的内核和超参数值。也就是说，降维通常是有监督学习任务（例如分类）的准备步骤，因此你可以使用网格搜索来选择在该任务上能获得最佳性能的内核和超参数。以下代码创建了一个两步流水线，首先使用kPCA将维度减少到二维，然后使用逻辑回归来分类。它使用GridSearchCV来查找kPCA的最佳内核和gamma值，以便在流水线的最后得到最好的分类准确率：

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
clf = Pipeline([
        ("kpca", KernelPCA(n_components=2)),
        ("log_reg", LogisticRegression(solver="lbfgs"))
    ])
param_grid = [{
        "kpca__gamma": np.linspace(0.03, 0.05, 10),
        "kpca__kernel": ["rbf", "sigmoid"]
    }]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)

然后，可以通过bestparams变量来得到最佳内核和超参数：

print(grid_search.best_params_)

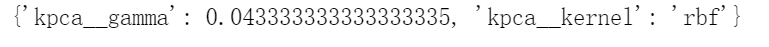
另一种完全无监督的方法是选择产生最低重构误差的内核和超参数。请注意，重建并不像使用线性PCA那样容易。以下是原因。图8-11显示了原始的瑞士卷3D数据集（左上）和使用RBF内核应用kPCA之后得到的2D数据集（右上）。多亏了内核技术，此变换在数学上等效于使用特征图φ将训练集映射到无限维特征空间（右下），然后使用线性PCA将变换后的训练集投影到2D。
请注意，如果我们可以对一个给定的实例在缩小的空间中反转线性PCA，则重构点将位于特征空间中，而不是原始空间中（例如，如图中的X所示）。由于特征空间是无限维的，因此我们无法计算重构点，无法计算真实的重构误差。幸运的是，有可能在原始空间中找到一个点，该点将映射到重建点附近，这一点称为重建原像。一旦你有了原像，就可以测量其与原始实例的平方距离。然后可以选择内核和超参数，最大限度地减少此重构原像误差。

你可能想知道如何执行这个重构。一种解决方案是训练有监督的回归模型，其中将投影实例作为训练集，将原始实例作为目标值。如果设置fit_inverse_transform=True，Scikit-Learn会自动执行此操作，如以下代码所示[2]：

rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433,
                    fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)

默认情况下，fit_inverse_transform=False，并且KernelPCA没有inverse_transform（）方法。仅当你设置fit_inverse_transform=True时，才会创建此方法。

计算重建原像误差：

from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)

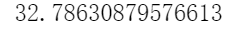
现在，你可以使用网格搜索与交叉验证来找到可最大限度减少此错误的内核和超参数.
[1] Bernhard Schölkopf et al.，“Kernel Principal Component Analysis”，in Lecture Notes in Computer Science 1327（Berlin：Springer，1997）：583–588.
[2] 如果设置fit_inverse_transform=True，Scikit-Learn将使用Gokhan H.Bakır等人的算法
（基于Kernel Ridge Regression）。“Learning to Find Pre-Images”，Proceedings of the 16th International Conference on Neural Information Processing Systems（2004）：449–456。

8.7 局部线性嵌入（Locally Linear Embedding)

局部线性嵌入（LLE）是另一种强大的非线性降维（NLDR）技术[1]。它是一种流形学习技术，不像以前的算法那样依赖于投影。简而言之，LLE的工作原理是首先测量每个训练实例如何与其最近的邻居（c.n.）线性相关，即假定样本点的坐标能够通过它的邻域样本进行线性组合而重构出来。然后寻找可以最好地保留这些局部关系的训练集的低维表示形式（稍后会详细介绍）。这种方法特别适合于展开扭曲的流形，尤其是在没有太多噪声的情下。

8.7.1 以瑞士卷例子来展示LLE算法

以下代码使用Scikit-Learn的LocallyLinearEmbedding类来展开瑞士卷：

from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)

plt.figure(figsize=(12,8),dpi=600)
plt.rc('font',family='SimHei')
plt.title("使用LLE展开的瑞士卷", fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)
plt.show()

8.7.2 LLE算法解析

LLE的工作方式如下：对于每个训练实例x(i)，算法都会识别出其k个最近的邻居（在前面的代码k=10中），然后尝试将x(i)重构为这些邻居的线性函数。更具体地说，它找到权重wi，j，使得x(i) 与之间的平方距离尽可能小，并假设如果x(j)不是x(i)的k个最接近的邻居之一则wi，j=0。因此，LLE的第一步是公式8-4中描述的约束优化问题，其中W是包含所有权重wi，j的权重矩阵。第二个约束条件只是简单地将每个训练实例x(i) 的权重归一化。
公式8-4：LLE第一步：局部关系线性建模

在此步骤之后，权重矩阵 （包含权重 ）对训练实例之间的局部线性关系进行编码。第二步是将训练实例映射到d维空间（其中d这种想法导致了公式8-5中描述的无约束优化问题。它看起来与第一步非常相似，但是我们没有保持实例固定并找到最佳权重，而是相反：保持权重固定并找到实例图像在低维空间中的最佳位置。注意Z是包含所有z(i)的矩阵。
公式8-5：LLE第二步：在保持关系的同时减少维度

Scikit-Learn的LLE实现具有以下计算复杂度：O（mlog(m)nlog(k)）用于找到k个最近的邻居，O（mnk3）用于优化权重，O（dm2）用于构造低维表示。不幸的是，最后一项中的m2使该算法很难扩展到非常大的数据集。
[1] Sam T.Roweis and Lawrence K.Saul，“Nonlinear Dimensionality Reduction by Locally Linear Embedding”，Science 290，no.5500（2000）：2323–2326.

8.8 其他降维技术

还有许多其他降维技术，Scikit-Learn中提供了其中几种。以下是一些很受欢迎的降维技术：
随机投影
顾名思义，使用随机线性投影将数据投影到较低维度的空间。这听起来可能很疯狂，但事实证明，这样的随机投影实际上很有可能很好地保持距离，就如William B.Johnson和Joram Lindenstrauss在著名引理中的数学证明。降维的质量取决于实例数目和目标维度，令人惊讶的不取决于初始维度。请查看sklearn.random_projection软件包的文档以获取更多详细信息。
多维缩放（MDS）
当尝试保留实例之间的距离时降低维度。
Isomap
通过将每个实例与其最近的邻居连接来创建一个图，然后在尝试保留实例之间的测地距离[1]的同时降低维度。
t分布随机近邻嵌入（t-SNE）
降低了维度，同时使相似实例保持接近，异类实例分开。它主要用于可视化，特别是在高维空间中可视化实例的聚类（例如，以2D可视化MNIST图像）。
线性判别分析（LDA）
LDA是一种分类算法，但是在训练过程中，它会学习各类之间最有判别力的轴，然后可以使用这些轴来定义要在其上投影数据的超平面。这种方法的好处是投影将使类保持尽可能远的距离，因此LDA是在运行其他分类算法（例如SVM分类器）之前降低维度的好技术。
图8-13显示了其中一些技术的结果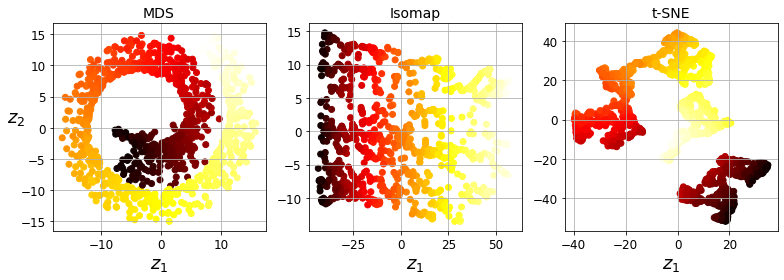

[1] 一个图中两个节点之间的测地距离是这些节点之间最短路径上的节点数。

8.9 练习题

1.减少数据集维度的主要动机是什么？主要缺点是什么？
2.维度的诅咒是什么？
3.一旦降低了数据集的维度，是否可以逆操作？如果可以，怎么做？如果不能，为什么？
4.可以使用PCA来减少高度非线性的数据集的维度吗？
5.假设你在1000维的数据集上执行PCA，将可解释方差比设置为95%。结果数据集将具有多少个维度？
6.在什么情况下，你将使用常规PCA、增量PCA、随机PCA或内核PCA？
7.如何评估数据集中的降维算法的性能？
8.链接两个不同的降维算法是否有意义？
9.加载MNIST数据集（在第3章中介绍），并将其分为训练集和测试集（使用前60000个实例进行训练，其余10 000个进行测试）。在数据集上训练随机森林分类器，花费多长时间，然后在测试集上评估模型。接下来，使用PCA来减少数据集的维度，可解释方差率为95%。在精简后的数据集上训练新的随机森林分类器，查看花费了多长时间。训练速度提高了吗？接下来，评估测试集上的分类器。与之前的分类器相比如何？
10.使用t-SNE将MNIST数据集降至两个维度，然后用Matplotlib绘制结果。你可以通过散点图用10个不同的颜色来代表每个图像的目标类，或者也可以用对应实例的类（从0到9的数字）替换散点图中的每个点，甚至你还可以绘制数字图像本身的缩小版（如果你绘制所有数字，视觉效果会太凌乱，所以你要么绘制一个随机样本，要么选择单个实例，但是这个实例的周围最好没有其他绘制的实例）。现在你应该得到了一个很好的可视化结果及各自分开的数字集群。尝试使用其他降维算法，如PCA、LLE或MDS等，比较可视化结果