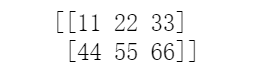矩阵的核心（上）：向量变换

矩阵？一排向量，一堆数

介绍完了向量，这一篇我们开始介绍矩阵。对于矩阵而言，最直观的描述就是一个 m×n 大小的数字方阵，它可以看作是 n 个 m 维列向量从左到右并排摆放，也可以看成是 m 个 n 维行向量从上到下进行叠放。
我们举一个实际的例子：一个 2×3的矩阵：

显而易见，它有 2 行 3 列，一共 6 个元素，每一个元素都对应矩阵中的一个数据项，例如第一行第二列的项是 2，我们也可以表示为 A12=7。
现在我们使用Python 语言里的NumPy 库中的嵌套数组来完成，这个矩阵本质上被表示成了一个二维数组。

import numpy as np
A = np.array([[3, 7, 6], 
              [0.3, -10, 22]])
print(A)
print(A.shape)

在形容矩阵规模的时候，一般采用其行数和列数来进行描述，对应到代码中，我们通过矩阵 A 的shape 属性，就获取了一个表示规模的元组：2 行 3 列。

一些重要的特殊矩阵

初步接触了上一小节里那个普普通通的 2×3矩阵后，这里我们再补充一些特殊形态的矩阵，这些矩阵的特殊性不光体现在外观形状上，更在后续的矩阵实际应用中发挥着重要的作用。

方阵：行数等于列数

行数和列数相等的这类矩阵，我们称之为方阵，其行数或列数称之为它的阶数，这里我们看到的就是一个 3 阶方阵：

我们用代码表示：

A = np.array([[1, 2, 3], 
              [4, 5, 6],
              [7, 8, 9]])
print(A)
print(A.shape)

矩阵转置与对称矩阵

在说到对称矩阵之前，我们先得说一下矩阵的转置。对于矩阵，如果将其行列互换得到一个新矩阵，我们将其称之为转置矩阵，行列互换的矩阵操作我们称之为矩阵的转置。

A = np.array([[1, 2, 3], 
             [4, 5, 6]])
print(A)
print("===============")
print(A.T)

那么，如果原矩阵和转置后新得到的矩阵相等，那么这个矩阵我们就称其为对称矩阵。显然，矩阵对称的前提必须得是一个方阵，其次在方阵 S 中的每一项元素，都必须满足Sij=Sji,我们举一个实际例子看看。

S = np.array([[1, 2, 3],
              [2, 5, 6],
              [3, 6, 9]])
print(S)
print("===============")
print(S.T)

在对阵矩阵中我们发现，沿着从左上到右下的对角线相互对称的元素都是彼此相等的。在后面的内容中你会不断发现：将对称矩阵称之为最重要的矩阵之一，丝毫不为过。它在矩阵的相关分析中会扮演极其重要的角色。

向量：特殊的一维矩阵

前面在介绍向量的时候，我们提到过这个概念。现在介绍了矩阵之后，我们再着重回顾一下：n 维的行向量可以看做是 1×n的矩阵，同理，n 维的列向量也同样可以看做是 n×1的特殊矩阵。
那么这样做的目的是什么呢？一方面可以将矩阵和向量的 Python 表示方法统一起来，另一方面，在马上要介绍的矩阵与向量的乘法运算中，也可以将其看作是矩阵与矩阵乘法的一种特殊形式，将计算方式统一起来。我们再次用这个视角重新生成一个新的行向量和列向量。

p = np.array([[2, 5, 8]])
print(p)
print("===============")
print(p.T)

我们用生成矩阵的方法生成了一个 1×3的矩阵，用它来表示一个 3 维的行向量。随后将其转置（因为是矩阵形式，所以可以运用转置方法），就得到了 3 维的列向量。

零矩阵：元素全 0

顾名思义，所有元素都是 0 的矩阵称之为零矩阵，记作 O，像下面这个 3×5的零矩阵。
，它可以记作是 O3,5
我们来看看如何用代码操作。

A = np.zeros([3, 5])
print(A)

对角矩阵

非对角元素位置上全部为 0 的方阵，我们称之为对角矩阵，例如：
用Python 生成的方法如下：

A = np.diag([3, 5, 7])
print(A)

单位矩阵：对角线为 1

注意：单位矩阵并不是所有元素都为 1 的矩阵，而是对角元素均为 1，其余元素均为 0 的特殊对角矩阵。n 阶单位矩阵记作,下面我们用 Python 生成一个 4 阶单位矩阵

I = np.eye(4)
print(I)

矩阵的基本运算

矩阵的加法

矩阵之间的加法必须运用到相等规模的两个矩阵之间，即：行数和列数相等的两个矩阵之间才能做加法运算。这个非常容易理解，将对应位置上的元素相加即可得到结果矩阵：

我们还是看看实际的代码。

A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = np.array([[10, 20, 30],
              [40, 50, 60]])
print(A+B)

矩阵的数量乘法

矩阵的数量乘法，描述起来也非常简单：

我们还是看看实际的代码的例子。

A = np.array([[1, 2, 3],
              [4, 5, 6]])
print(3*A)

矩阵与矩阵的乘法

矩阵与矩阵的相乘，过程要稍微复杂一点，因此我们拿出来单讲。例如下面举例的矩阵 A 和矩阵 B 的乘法运算，对两个矩阵的形态是有要求的。

仔细观察这个计算公式，我们总结出以下的一些要求和规律：

1. 左边矩阵的列数要和右边矩阵的行数相等
2. 左边矩阵的行数决定了结果矩阵的行数
3. 右边矩阵的列数决定了结果矩阵的列数

同样，我们用 Python 来演示下面这个例子：

import numpy as np
A = np.array([[1, 2],
              [3, 4],
              [5, 6]])
B = np.array([[3, 4, 5],
              [6, 7, 8]])
print(np.dot(A, B))

改变空间位置：矩阵乘以向量的本质

矩阵与向量的乘法，一般而言写作矩阵 A 在左，列向量 x 在右的 Ax 的形式。这种 Ax 的写法便于描述向量 x 的位置在矩阵 A 的作用下进行变换的过程（下面会详细介绍）。
矩阵与向量的乘法，其实可以看作是矩阵与矩阵乘法的一种特殊形式，只不过位于后面的矩阵列数为 1 而已。

我们对照前面讲过的矩阵与矩阵的乘法，来对比一下矩阵与向量的乘法规则，我们把列向量看作是列数为 1 的特殊矩阵，那么就会非常明确：

1. 矩阵在左，列向量在右，矩阵的列数和列向量的维数必须相等
2. 矩阵和向量相乘的结果也是一个向量
3. 矩阵的行数就是最终结果输出的列向量的维数
4. 乘法的规则如上所示，就是矩阵的每行和列向量进行对应元素分别相乘后相加

我们来看一个矩阵与列向量相乘的例子：

A = np.array([[1, 2],
              [3, 4],
              [5, 6]])
x = np.array([[4, 5]]).T
print(np.dot(A, x))

从结果看，原始向量表示二维空间中的一个点，坐标为 (4,5)，经过矩阵乘法的作用，转化为三维空间中坐标为 (14,32,50) 的点。
因此从这个例子中我们可以总结一下矩阵的作用：在特定矩阵的乘法作用下，原空间中的向量坐标，被映射到了目标空间中的新坐标，向量的空间位置（甚至是所在空间维数）由此发生了转化。

从行的角度思考

学习了矩阵、向量的表示方法以及运算规则之后，我们回过头来静静的思考一个问题：矩阵 A 和列向量 x 的乘法 Ax 到底意味着什么？下面，我们就来挖掘一下这里面的内涵。
在二阶方阵 A 与二维列向量 x 相乘的例子中：

刚才说了，位于矩阵 A 第 i 行的行向量的各成分和列向量 x 各成分分别相乘后相加，得到的就是结果向量的第 i 个成分。这个计算方法有没有感觉很熟悉？没错，这不就是向量点乘的定义式么？
即：
矩阵与向量的乘法如果从行的角度来看，就是如此。常规的计算操作就是这么执行的，但是似乎也没有更多可以挖掘的，那我们试试继续从列的角度再来看看。

列的角度：重新组合矩阵的列向量

如果从列的角度来计算矩阵与向量的乘积，会有另一套计算的方法，可能大家对这种方法要相对陌生一些。但是实质上，这种方法从线性代数的角度来看，还要更为重要一些，我们还是用二阶方阵进行举例。

发现了规律没有？我们通过这种形式的拆解，也能得到最终的正确结果，这就是从列的角度进行的分析。从前面的知识我们可以这样描述：
从列的角度来看，矩阵 A 与向量 x 的乘法是对矩阵 A 的各列向量进行线性组合的过程，每个列向量的组合系数就是向量 x 的各对应成分。
这么理解似乎有点新意，我们按照列的思想重新把矩阵 A 写成一组列向量的形式：

所得到的结果就是矩阵第一列的列向量的3倍，的5倍。因此，一个矩阵和一个向量相乘的过程，就是对位于原矩阵各列的列向量重新进行线性组合的过程，而线性组合的各系数就是向量的对应各成分。

进一步引申：变换向量的基底

二阶方阵与二维列向量乘法举例

为了方便说明原理，我们依旧用二阶方阵与列向量举相乘例。
二维列向量的坐标是(x,y)。还记得之前我们介绍过的向量坐标的概念么？向量的坐标依托于基底的选取，向量坐标在基底明确的前提下才有实际意义，而这个二维列向量，我们说它的坐标是(x,y)，基于的就是默认基底那么二维列向量的完整表达式就是：。
好，回顾了这些基础，我们就利用它将矩阵与向量的乘法表达式做进一步的展开：

是不是已经初见端倪了？我们再直观地展示一下式子首尾的结果，在矩阵的乘法作用下，向量完成了下面的转换：相当于把原坐标(x,y)变换为以新的基底为参考系的新坐标(ax+by,cx+dy)。让我们通过下面两幅图，来看看这个过程是如何完成空间转换的。


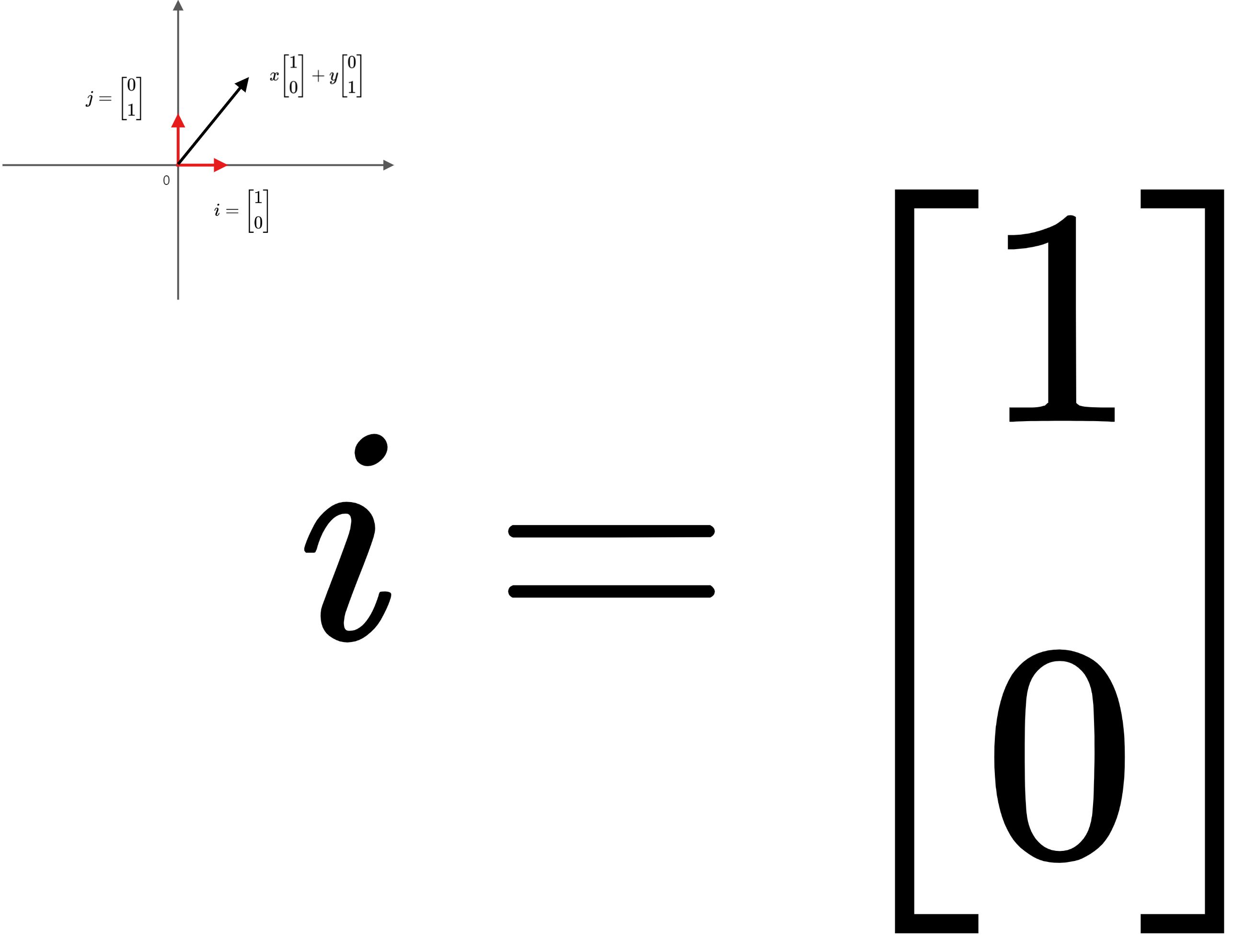
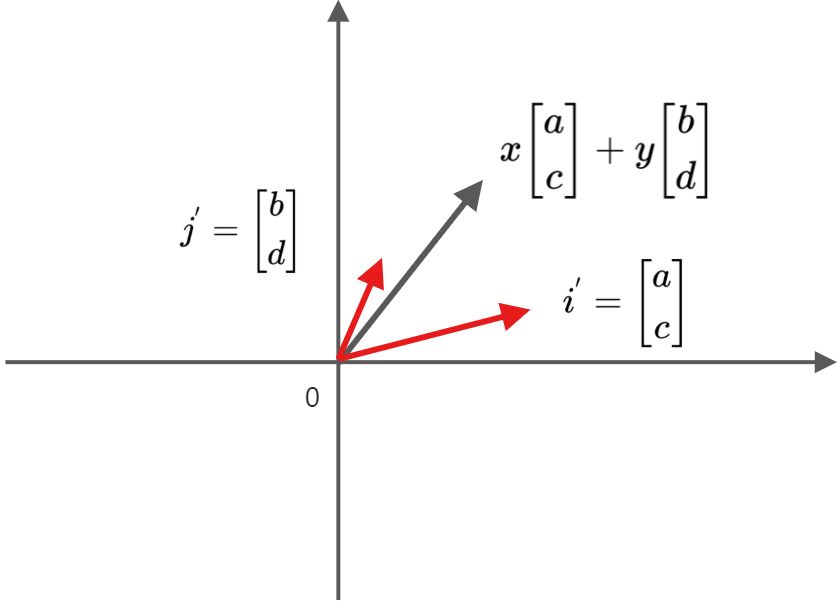
结合矩阵的式子我们不难发现：矩阵 A 的第一列就是原始的默认基向量变换后的目标位置（新的基向量），而第二列就是另一个基向量映射后的目标位置（新的基向量）。基底的变换明确了，那向量的坐标呢？映射后得到的新向量，如果以为基底，它的坐标仍是 (x,y) ，如果以默认的为基底，那么其坐标就是 (ax +by,cx+dy)。

扩展到三阶方阵

为了让结果更让人信服，我们再看看三阶方阵和三维列向量相乘的例子，同理也满足这个过程：

是不是和二阶矩阵的情况是一模一样呢？三阶方阵将三维列向量的基底做了映射转换，方阵的第一列是原始基向量映射后的目标位置（新的基向量），方阵的第二列是原始基向量映射后的目标位置（新的基向量），方阵的第三列是原始基向量映射后的目标位置（新的基向量）。
因此同样的，映射后的目标向量如果在新的基底坐标值由原来默认基底下的坐标(x,y,z)变换为(ax+by+cz, dx+ey+fz, gx+hy+iz)。

一般化的：m×n 矩阵乘以 n 维列向量

此处，我们看到的就是最一般的情况了，矩阵 A=和向量进行相乘。
在 m×n 矩阵 A 的作用下，原始的 n 维基向量 映射成了新的基向量：，n 维基向量
映射成了，我们发现，在这种一般性的情况下，如果(m为行数，n为列数)那么映射前后，基向量的维数甚至都可能发生变化，n 维列向量 x 变换成了 n 个 m 维列向量线性组合的形式，其最终结果是一个 m 维的列向量。
由此看出，映射后的向量维数和原始向量维数的关系取决于 m 和 n 的关系，如果 m>n，那么目标向量的维数就大于原始向量的维数，如果 m

基变换的意外情况

实质上，如果仅仅停留在上面的讨论结果，那可能会显示出我们思考问题不够全面、准确。首先，“经过矩阵变换，会将原始的基底变换成为一组新的基底”这句话的表述就并不准确，之前这么说只是为了方便大家理解并建立概念。
为什么这么说呢？对于一个 m×n (m行n列)的矩阵 A 和 n 维列向量 x，经过 Ax 的乘法作用，x 的 n 个 n 维默认基向量构成的基底被转换成了 n 个 m 维的目标向量。

• 当 n>m 的时候，这 n 个向量线性相关，因此不构成基底；
• 当 n<m 的时候，即使这 n 个向量线性无关，由于它们不能表示 m 维空间中的所有向量，因此也不能称之为基底；
• 当且仅当 n=m，且这 n 个向量线性无关的时候，它们才能称之为一组新的基底。

不过即便有这些意外情况，我们这一讲里讨论的内容仍然具有重要意义，矩阵 A 的各列向量是 x 默认基底经过转换后的目标向量，正因为其在维度和线性相关性方面存在各种不同情况，因此这组目标向量的张成空间和原始向量所在的空间之间，就会存在多种不同的对应关系，这便是我们后续将要重点讨论的空间映射相关内容。