线性代数基础

1.1线性代数有什么用？

作为 《机器学习里的数学基础》 系列的第一部分，我们先开始讨论机器学习里的线性代数。
作为利用空间来投射和表征数据的基本工具，线性代数可以灵活地对数据进行各种变换，从而让研究人员更为直观、清晰地探查到数据的主要特征和不同维度所需的信息。因此，线性代数的核心地位不言而喻，只有熟练运用好这个工具，才能搭建起攀登机器学习的牢固阶梯。
机器学习和数据分析中究竟会有哪些地方需要用到线性代数？

• 量化描述日常生活中的事物，比如个体的不同属性、自然语言中的词语、句子等等，用于支撑我们所要进行的算法分析
• 将待处理的数据在不同维度的空间中进行变换处理，以找到最佳的观测角度，使得数据处理达到最好效果
• 从采样的海量数据中提取出主要特征成分，梳理出数据的主要脉络，从而指导你对一个文本进行主题建模，帮助你利用协同过滤技术成功给用户推荐最喜爱的菜肴
• 用数字表示图像，并且在不太影响观察效果的前提下，利用很小的存储空间近似达到原有图像的视觉效果
• 对采集到的观测数据进行拟合，帮助我们找到其中暗含的规律，指导对未知数据的预测
• 在实际的数据采样分析过程中，在无法找到精确解的情况下，探索到最接近真相的近似解

这些实用而有趣的问题，我们在数据分析和机器学习中几乎时时都会遇到。而想要解决好这些问题，线性代数的核心概念和思想方法都是必须要牢固掌握的，

1.2学习思路

贯穿整个线性代数的主干是空间变换，我们将从构筑空间、空间投影、矩阵特征、数据降维这四大纬度，聚焦线性代数与机器学习算法结合最紧密的核心内容。
第 1 部分：构筑空间。这一部分我们将从空间坐标表示与线性变换入手，快速建立线性代数的直观感受，理解向量和矩阵运算的几何意义。同时探索空间——这个线性代数的概念基石，理解空间中的映射和变换的本质，深入学习矩阵在其中的灵魂作用。
第 2 部分：空间投影。这一部分我们将从空间投影的现象入手，将理论和工程进行紧密结合，掌握线性代数在近似与拟合中的理论基础，学习最小二乘法的原理与实际应用，并实践线性拟合、无解方程组的近似解问题。
第 3 部分：矩阵特征。这一部分是矩阵分析的核心重点，我们需要深刻领会矩阵相似性的几何意义以及特征值、特征向量的提取方法，用以打好数据降维的理论基础。
第 4 部分：数据降维。这一部分是整个线性代数知识脉络的交汇点，可以说是矩阵分析中最为精彩的地方。利用前面打下的概念基础，我们将深入地学习特征值分解和奇异值分解的方法，并利用这些工具进行数据的压缩和降维，实现对样本数据的主成分分析。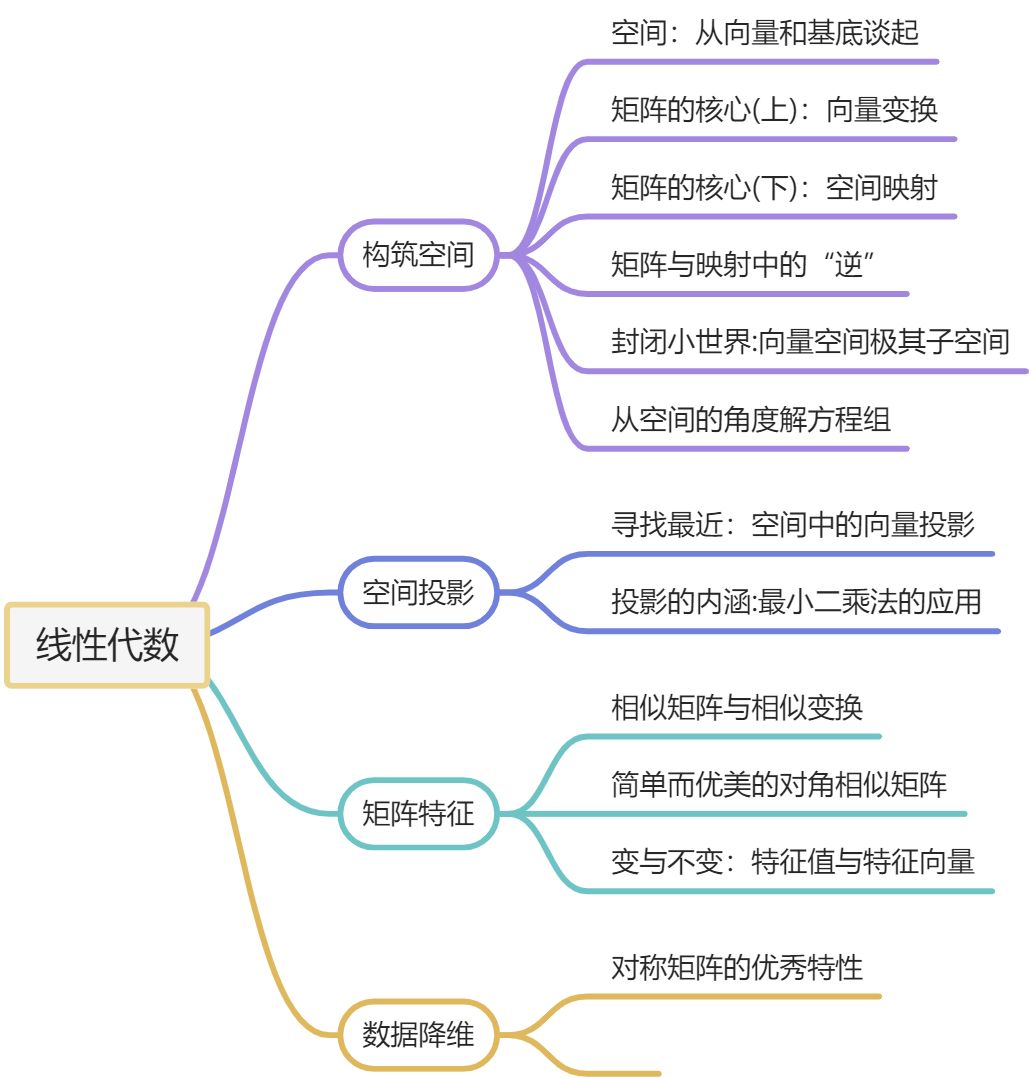

现在让我们一起开始这段学习旅程！
万丈高楼平地起，希望《机器学习中的数学基础》能陪伴大家走好机器学习的学习与实践的必经之路、梳理纷繁复杂的知识网络、构筑好算法模型的数学基础。更重要的是，我希望大家能一起形成一种思维习惯：源于理论，我们条分缕析；面向实践，我们学以致用。 有了扎实的数学理论和方法基础，才能顺利走进AI人工智能领域的神奇大门！