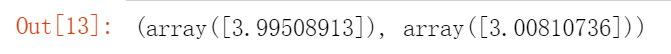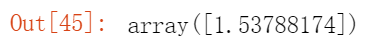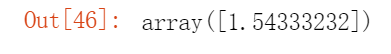到目前为止,我们已经探讨了不同机器学习的模型,但是它们各自的训练算法在很大 程度上还是一个黑匣子。回顾前几章里的部分案例,你大概感到非常惊讶,在对系统内部 一无所知的情况下,居然已经实现了这么多:优化了一个回归系统,改进了一个数字图片分类器,从零开始构建了一个垃圾邮件分类器,所有这些,你都不知道它们实际是如何工 作的。确实是这样,在许多情况下,你并不需要了解实施细节。 但是,很好地理解系统如何工作也是非常有帮助的。针对你的任务,它有助于快速定 位到合适的模型、正确的训练算法,以及一套适当的超参数。不仅如此,后期还能让你更 高效地执行错误调试和错误分析。最后还要强调一点,本章探讨的大部分主题对于理解、 构建和训练神经网络(本书第二部分)是至关重要的。
本章我们将从最简单的模型之一——线性回归模型,开始介绍两种非常不同的训练模 型的方法:
- 通过“闭式”方程,直接计算出最拟合训练集的模型参数(也就是使训练集上的成本函数最小化的模型参数)。
- 使用迭代优化的方法,即梯度下降(GD),逐渐调整模型参数直至训练集上的成本函数调至最低,最终趋同于第一种方法计算出来的模型参数。我们还会研究几个梯度下降的变体,包括批量梯度下降(Batch GD)、小批量梯度下降(Mini-batch GD)以及随机梯度(Stochastic GD)下降。等我们进入到第二部分 神经网络的学习时,会频繁地使用这几个的变体。
接着我们将会进入多项式回归的讨论,这是一个更为复杂的模型,更适合非线性数据集。由于该模型的参数比线性模型更多,因此更容易造成对训练数据过拟合,我们将使用 学习曲线来分辨这种情况是否发生。然后,再介绍几种正则化技巧,降低过拟合训练数据 的风险。
最后,我们将学习两种经常用于分类任务的模型:Logistic回归和Softmax回归。
本章将会出现不少数学公式,需要用到线性代数和微积分的一些基本概念。要理解这些方程式,你需要知道什么是向量和矩阵,如何转置向量和矩阵,什么是点积、逆矩阵、偏导数。如果你不熟悉这些概念,请先通过在线资料,进行线性代数和微积分的入门学习。对于极度讨厌数学的读者,还是需要学习这一章,但是可以跳过那些数学公式,希望文字足以让你了解大多数的概念。
4.1 线性回归
在第一章,我们介绍了一个简单的生活满意度回归模型: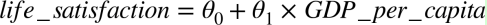
这个模型仅仅是输入量GDPper_capita的线性函数,θ0和θ1是这个模型的参数,线性模型更一般化的描述指通过计算输入变量的加权和,并加上一个常数偏置项(截距项)来得到一个预测值。如公式 4-1:
公式 4-1:线性回归预测模型

- y_hat表示预测结果
- n表示特征的个数
- xi表示第i个特征的值
- θj表示第j个参数(包括偏置项θ0和特征权重值θ1, θ2, …, θn)
上述公式可以写成更为简洁的向量形式,如公式 4-2:
公式 4-2:线性回归预测模型(向量形式)
- θ表示模型的参数向量包括偏置项θ0和特征权重值θ1到θn
- x为每个样本中特征值的向量形式,包括x1到xn,而且x0恒为 1
- θ· x表示θ和x的点积,它等于
- hθ表示参数为θ的假设函数
在机器学习中,向量通常表示为列向量,是有单一列的二维数组。如果θ和x为列向量,则预测为
,其中θT为θ的转置(转置后列向量θ变为行向量θT),且θ**T**x为θT和x的 矩阵乘积。当然这是相同的预测,除了现在是以单一矩阵表示而不是一个标量值。在本书中,我将使用这种表示法来避免在点积和矩阵乘法之间切换。
这就是线性回归模型,我们该怎样训练线性回归模型呢?回想一下,训练模型就是设置模型参数直到模型最拟合训练集的过程。为此,我们首先需要知道怎么测量模型对训练数据的拟合程度是好还是差。在第2章中,我们了解到回归模型最常见的性能指标是均方根误差(RMSE)(见公式2-1)。因此,在训练线性回归模型时,你需要找到最小化 RMSE的θ值。在实践中,将均方误差(MSE)最小化比最小化RMSE更为简单,二者效果 相同(因为使函数最小化的值,同样也使其平方根最小)[1] 。
这些符号大多数在第2章中提到过,唯一的区别是h换成了hθ,以便清楚地表明模型被向量θ参数化。为了简化符号,我们将MSE(X,hθ)直接写作MSE(θ)。
4.1.1标准方程
为了得到使成本函数最小的θ值,有一个闭式解方法——也就是一个直接得出结果的数学方程,即标准方程(见公式4-4)。
公式4-4:标准方程
这个方程中:
是使成本函数最小的θ值。
- y是包含y(1)到y(m)的目标值向量。
我们生成一些线性数据来测试这个公式(见图4-1):
import numpy as npimport matplotlib.pyplot as pltX = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.randn(100, 1)plt.plot(X, y, "b.")plt.axis([0, 2, 0, 15])plt.figure(figsize=(16, 8),dpi=600)plt.show()
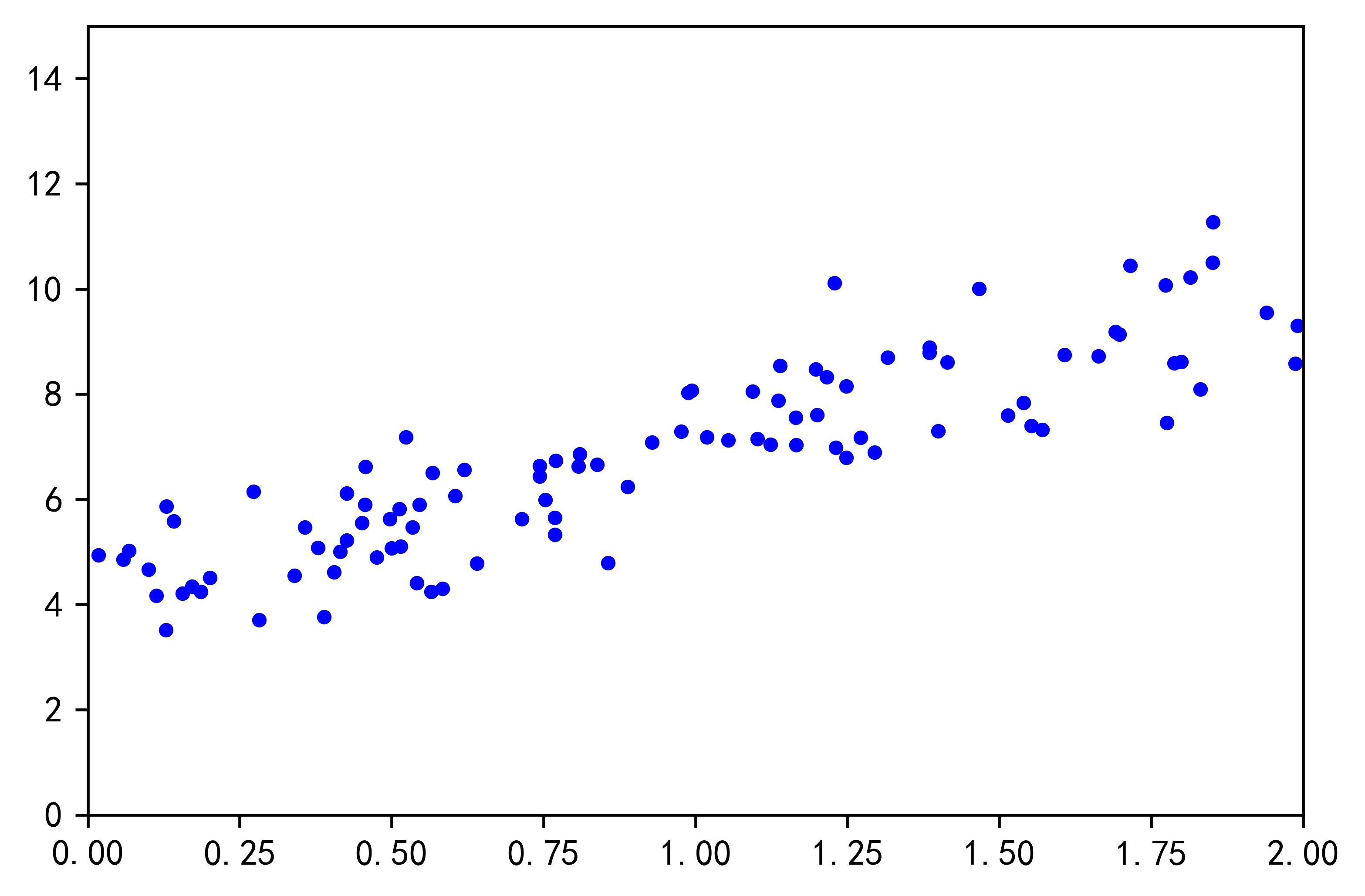
现在我们使用标准方程来计算 。使用NumPy的线性代数模块(np.linalg)中的inv()函数来对矩阵求逆,并用dot()方法计算矩阵的内积:
X_b = np.c_[np.ones((100, 1)), X] # add x0 = 1 to each instancetheta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)theta_best

我们期待的是θ0=4,θ1=3,得到的是θ0=4.082,θ1=3.108。非常接近,噪声的存在使其不可能完全还原为原本的函数。 在可以用现做出预测:
X_new = np.array([[0], [2]])X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instancey_predict = X_new_b.dot(theta_best)y_predict

绘制模型的预测结果(见图4-2):
plt.plot(X_new, y_predict, "r-", linewidth=2, label="预测值")plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.rc('font',family='SimHei')plt.legend(loc="upper left", fontsize=14)plt.axis([0, 2, 0, 15])plt.figure(figsize=(16, 8),dpi=600)plt.show()
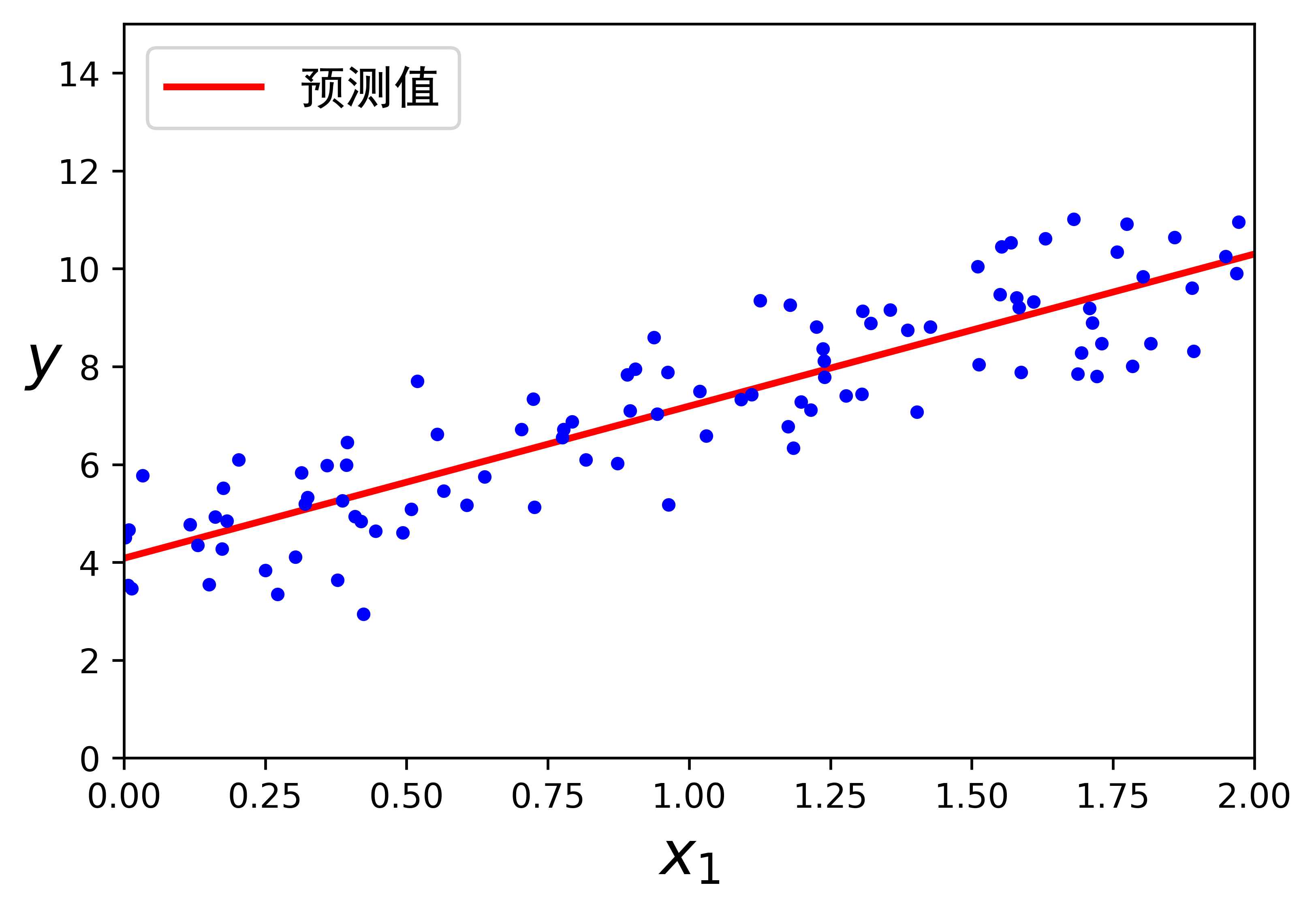
使用Scikit-Learn执行线性回归很简单:[2]
from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()lin_reg.fit(X, y)lin_reg.intercept_, lin_reg.coef_
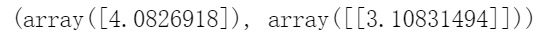
LinearRegression类基于scipy.linalg.lstsq()函数(名称代表“最小二乘”),你可以直接调用它:
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)theta_best_svd

此函数计算 ,其中X+是X的伪逆(具体来说是Moore-Penrose逆)。你可以使用np.linalg.pinv()来直接计算这个伪逆:
np.linalg.pinv(X_b).dot(y)

伪逆本身是使用被称为奇异值分解(Singular Value Decomposition,SVD)的标准矩阵分解技术来计算的,可以将训练集矩阵X分解为三个矩阵U Σ V**T的乘积(请参阅numpy.linalg.svd())。伪逆的计算公式X+=VΣ+UT。为了计算矩阵Σ+,该算法取Σ并将所有小于一个小阈值的值设置为零,然后将所有非零值替换成它们的倒数,最后把结果矩阵转置。这种方法比计算标准方程更有效,再加上它可以很好地处理边缘情况:的确,如果矩阵XT X**是不可逆的(即奇异的),标准方程可能没有解,例如m
4.1.2计算复杂度
标准方程计算XT X的逆,XT X是一个(n+1)×(n+1)的矩阵(n是特征数量)。对这种矩阵求逆的计算复杂度通常为O(n2.4)到O(n3)之间,取决于具体实现。换句话说,如果将特征数量翻倍,那么计算时间将乘以大约22.4=5.3倍到23=8倍之间。Scikit-Learn的LinearRegression类使用的SVD方法的复杂度约为O(n2)。如果你将特征数量加倍,那计算时间大约是原来的4倍。
特征数量比较大(例如100 000)时,标准方程和SVD的计算将极其缓慢。好的一面是,相对于训练集中的实例数量(O(m))来说,两个都是线性的,所以能够有效地处理大量的训练集,只要内存足够。
同样,线性回归模型一经训练(不论是标准方程还是其他算法),预测就非常快速:因为计算复杂度相对于想要预测的实例数量和特征数量来说都是线性的。换句话说,对两倍的实例(或者是两倍的特征数)进行预测,大概需要两倍的时间。现在,我们再看几个截然不同的线性回归模型的训练方法,这些方法更适合特征数或者训练实例数量大到内存无法满足要求的场景。
[1] 通常情况下,学习算法会尝试优化与评估最终模型的性能指标不同的函数。通常,这是因为该函数更易于计算,它具有性能度量所缺乏的有用的微分特性,或者因为我们希望在训练过程中约束模型,如我们在讨论正则化时所看到的。
[2] 请注意,Scikit-Learn将偏差项(intercept)与特征权重(coef)分开。
4.2 距离与范数
通常我们说的距离有空间上的距离,比如东京距离大阪400公里。也有时间上的距离,比如距离圣诞节还有120天。那现在我们要探讨的是在向量的内积空间中距离是如何理解的。
设某个内积空间中有向量 和 ,这两个向量的起点位于坐标原点,向量间的距离就是指它们的终点——对应于坐标系中的两个点——之间的距离。
定义:内积空间中的向量之间的距离记作:
。
定义为:
显然,距离的具体计算方法,是由内积的函数形式确定的。对于欧几里得空间,也就是用点积作为内积的具体函数形式,两个向量之间的距离就称为欧几里得距离,在三维几何空间中,就等同于我们所熟知的“两点间的距离”。
4.2.1 欧几里得距离
依据点积的定义,欧几里得距离(Euclidean Distance)定义如下。
设向量和
是欧几里得空间的两个向量,它们之间的距离是:
如果对应为平面几何,则如图4-3所示,就是计算A,B两点的距离,根据平面几何知识,容易求得。
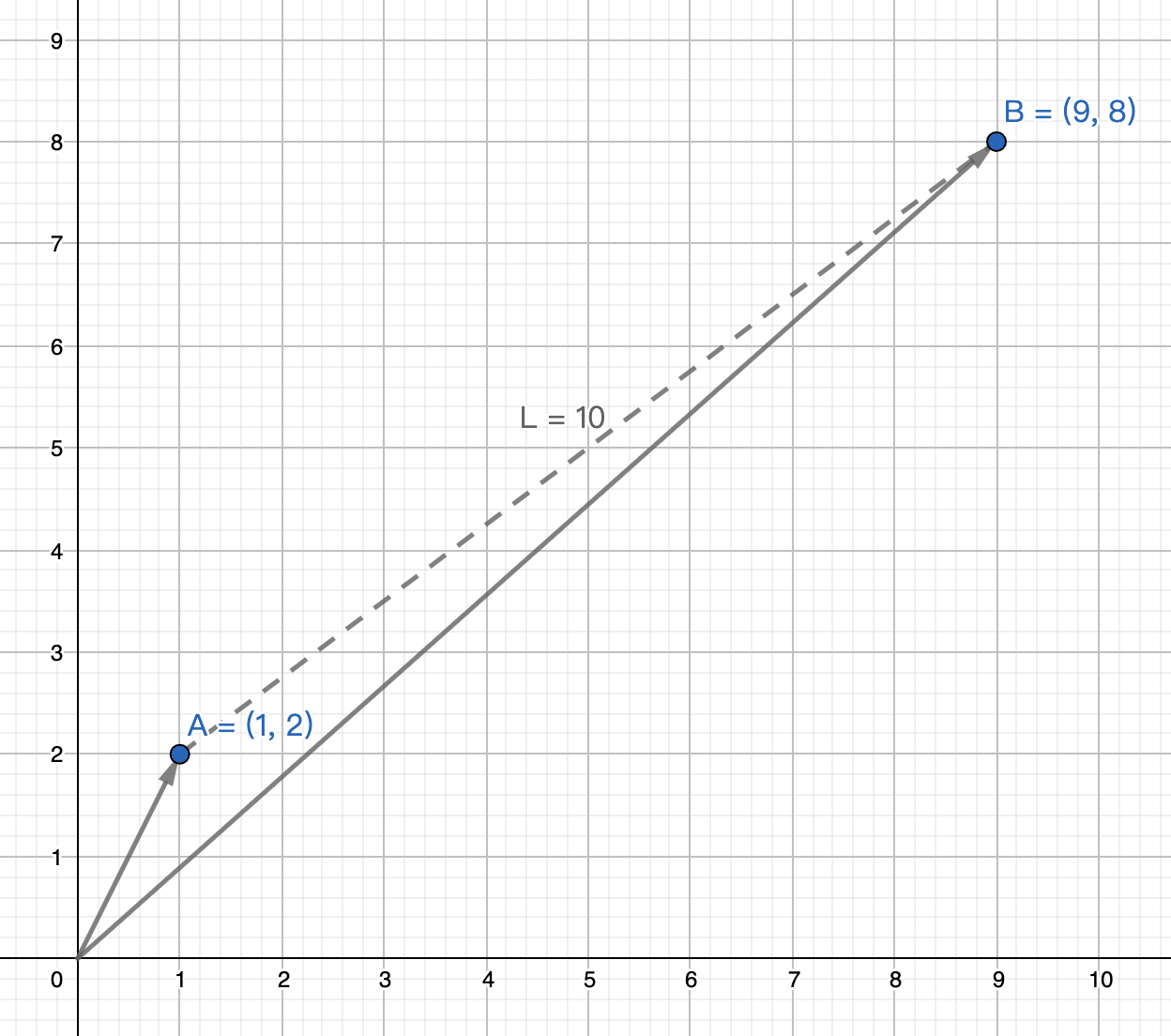
我们也可以用Numpy中linalg中的方法直接求得
import numpy as npvec1 = np.array([1, 2])vec2 = np.array([9, 8])dist = np.linalg.norm(vec1 - vec2)print(dist)
欧几里得距离是线性代数教材所讨论的距离,但是,在机器学习中和生活生产实践中,有时候用其他方式定义距离更方便,下面列举常见的几个。
4.2.2 曼哈顿距离
曼哈顿距离(Manhattan Distance),也称出租车距离或城市街区距离。曼哈顿是美国纽约市(New York City)的中心区,它的大部分道路呈黑棋盘格形状,如图4-4所示。
在如棋盘布局的街道上,从一点到另外一点,不论怎么走,距离都差不多。考虑理想化情况,如图4-5中的标记所示。如果从点A(1,5)出发,到点B(6,2),则可以有多种路径,例如:
- A→C→D→E→B,长度为8个单位
- A→F→B,长度为8个单位
- A→G→B,长度为8个单位
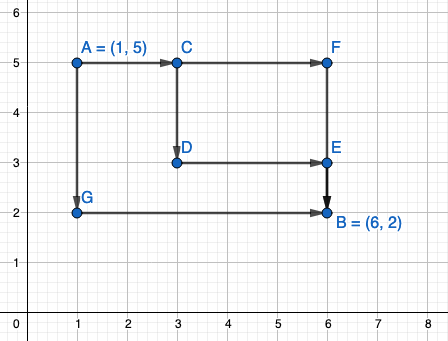
德国数学家闵可夫斯基(Hermann Minkowskin,四维时空理论的创立者)根据图4-5所示的特点,命名了曼哈顿距离。
设向量和
是两个向量,它们之间的曼哈顿距离是:
那么例如图4-5中的两个向量u(1,5),v(6,2)的曼哈顿距离即为:
同样利用Python中Scipy库的Cityblock()函数直接求出两个向量之间的曼哈顿距离。
from scipy.spatial.distance import cityblocka = np.array([2,3,4])b = np.array([9,8,7])Manhattan_Distance = cityblock(a, b)Manhattan_Distance
4.2.3 切比雪夫距离
以俄罗斯数学家切比雪夫命名的切比雪夫距离(Chebyshev Distance),定义如下。设向量和
是两个向量,它们之间的切比雪夫距离是:
即: 和 的对应坐标差的绝对值集合中最大的值。那么例如图4-5中的两个向量u(1,5),v(6,2)的切比雪夫距离即为:切比雪夫距离的另外一种等价表达方式是:
于是也将切比雪夫距离称为距离。切比雪夫他的大名在概率论中还会出现——切比雪夫不等式,而且他还有一个得意门生:安德雷·马尔可夫(Andrey Andreyevich Markov), 随机过程中的马尔科夫链就是他的研究成果。
4.2.4 闵可夫斯基距离
从数学角度来看,将前述对距离的定义一般化,就是闵可夫斯基距离(Minkowski Distance)。设向量和
是两个向量,它们之间的闵可夫斯基距离是:
当p=1,,即为曼哈顿距离。
当p=2,,即为欧几里得距离。
当p→,
,即为切比雪夫距离。
这里用闵可夫斯基距离作为更一般化的定义,是要纪念这位伟大的数学家、物理学家,他创立了闵可夫斯基时空(四维时空),为后来爱因斯坦建立广义相对论提供了框架。
4.2.5 基于距离的分类
距离在机器学习当中有着非常广阔的应用,就是最典型的就是分类。如何分类?机器学习中有一种方法,根据两个样本的数据计算它们之间的距离,距离越小,则代表它们之间的相似度越高,归为一类的概率就越大。据有关资料说明,社会心理学将人际距离分为四种:
- 亲密距离:0~0.5米;
- 个人距离:0.45~1.2米;
- 社会距离:1.2~3.5米;
- 公众距离:3.5~7.5米。
借助人与人之间的距离,就可以将人划分为不同的社会关系。在机器学习中,我们也常常用类似的方式,通过距离决定样本的类别。下面从鸢尾花数据集Iris中选出两个特征Petal length和Petal width,即花瓣长度和宽度。通过花与花之间的距离,能否区分他们species类别也就是对数据集进行分类。
plt.figure(dpi=600)X = iris["data"][:, (2, 3)] # petal length, petal widthy = (iris["target"] == 2).astype(np.int)plt.plot(X[y==0, 0], X[y==0, 1], "bs")plt.plot(X[y==1, 0], X[y==1, 1], "g^")plt.text(3.5, 1.5, "Not Iris virginica", fontsize=8, color="b", ha="center")plt.text(6.5, 2.3, "Iris virginica", fontsize=8, color="g", ha="center")plt.xlabel("Petal length", fontsize=14)plt.ylabel("Petal width", fontsize=14)plt.axis([2.9, 7, 0.8, 2.7])plt.show()
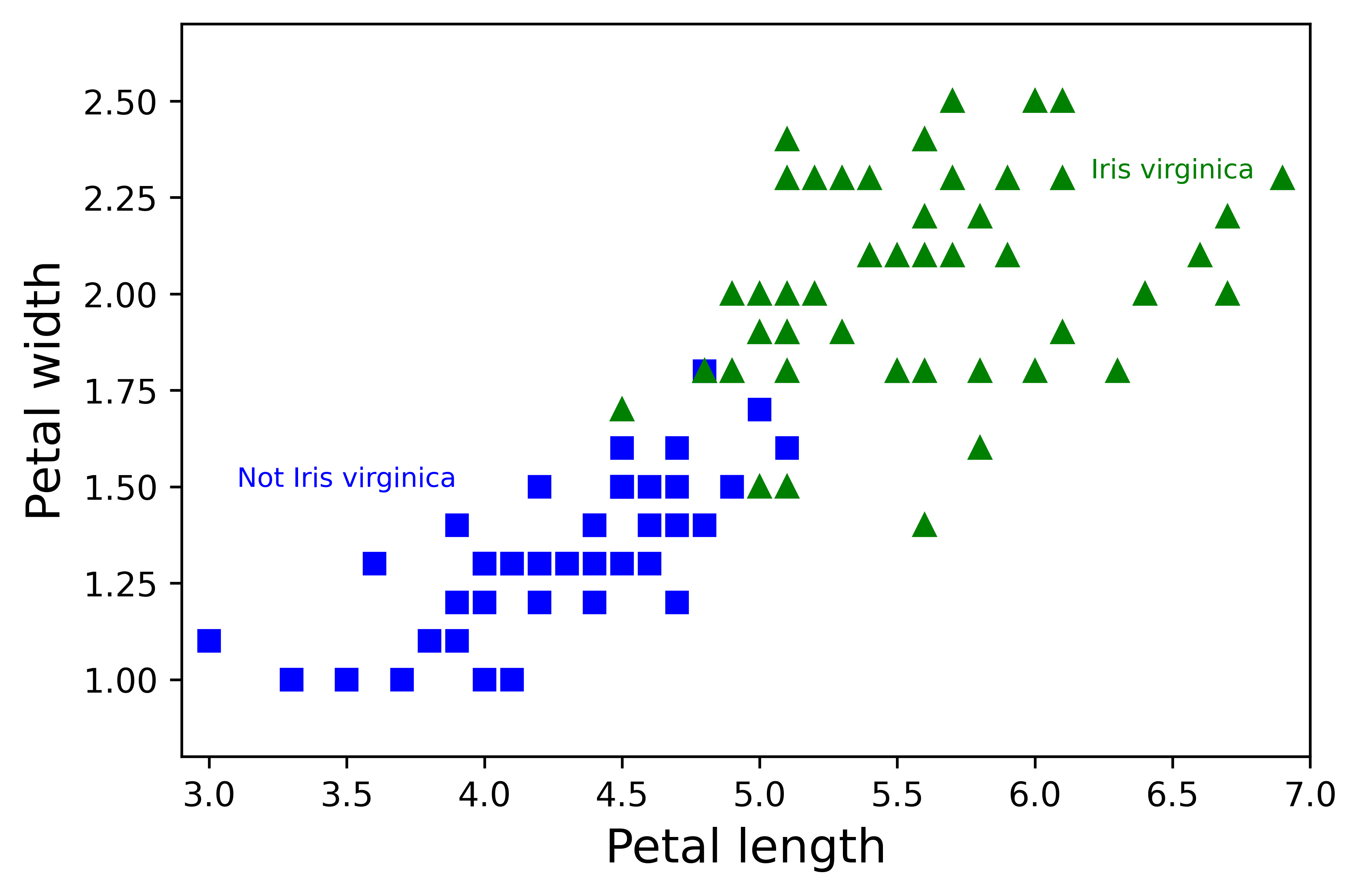
很显然,如图4-6 所示同一类别的鸢尾花“聚集”在一起,即彼此之间的“花际距离”比较近。那么,如果我们在每个类别中选一个相对中心的位置,并以此中心画一个圆,如果某样本到“中心”的距离不超过圆的半径,就可以认为该样本属于“中心”所在的类别。机器学习中的k-最近邻算法(k-Nearest Neighbors Algorithm,k-NN算法)就是基于这个设想发展而来的。
KNeighborsClassifier是sklearn中用于实现k-NN算法的模型,其中metric=’minkowski’,默认值为字符串’minkowski’,表示使用闵可夫斯基距离;另外一个参数默认值p=2,意味着令4.2.3节中介绍的闵可夫斯基距离中的p=2,即具体应用的是欧几里得距离;如果设置p=1,则应用曼哈顿距离。
4.2.6 范数
了解距离之后,探讨范数,会发现它不过是一种特殊情况。内积空间中两个向量的距离为如果其中一个向量是零向量,设v=0则可以得到
即:
其实,这个式子表示了一个向量的终点和起点之间的距离,因此,它被称为向量的长度、大小或范数(norm)。在欧几里得空间,根据点积的定义,范数的具体计算方法为:
由于它是欧几里得空间中的计算方式,所以被称为欧几里得范数,又因为要对每个坐标的平方后求和,所以还被称为范数,除
范数之外,与4.2.2中的曼哈顿距离类似,也有曼哈顿范数,又被称为
范数:
对于范数,还可以使用NumPy中的函数np.linalg.norm(),通过设置参数ord的值计算不同类型的范数类型。例如计算范数:
import numpy as npa = np.array([[3], [4]])L1 = np.linalg.norm(a, ord=1)print(L1)
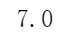
如果不设置参数ord的值,则默认为None,对于向量而言,就是计算范数。
L2 = np.linalg.norm(a)L2
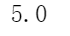
4.3 梯度下降
梯度下降是一种非常通用的优化算法,能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。
假设你迷失在山上的浓雾之中,你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。这就是梯度下降的做法:通过测量参数向量θ相关的误差函数的局部梯度,并不断沿着降低梯度的方向调整,直到梯度降为0,到达最小值!
具体来说,首先使用一个随机的θ值(这被称为随机初始化),然后逐步改进,每次踏出一步,每一步都尝试降低一点成本函数(如MSE),直到算法收敛出一个最小值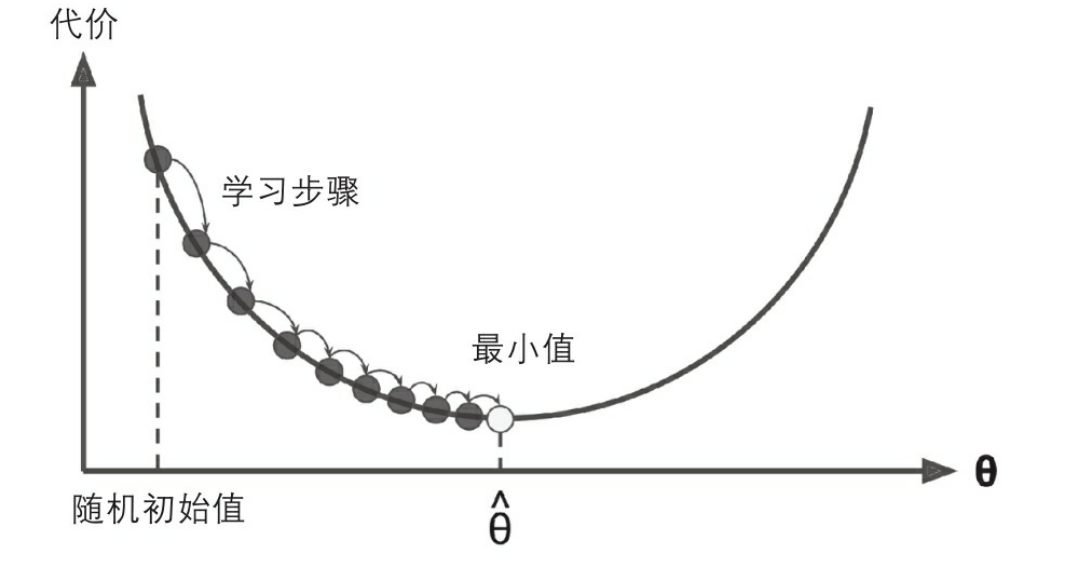
在梯度下降的描述中,模型参数被随机初始化并反复调整使成本函数最小化。学习步长与成本函数的斜率成正比,因此,当参数接近最小值时,步长逐渐变小。梯度下降中一个重要参数是每一步的步长,这取决于超参数学习率。如果学习率太低,算法需要经过大量迭代才能收敛,这将耗费很长时间。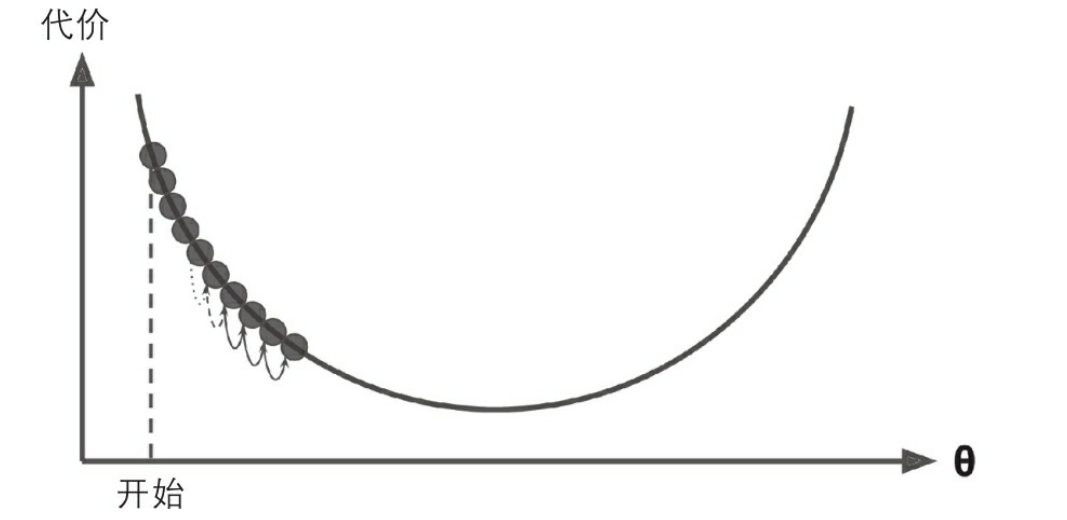
反过来说,如果学习率太高,那你可能会越过山谷直接到达另一边,甚至有可能比之前的起点还要高。这会导致算法发散,值越来越大,最后无法找到好的解决方案(参见图 4-9)。
最后,并不是所有的成本函数看起来都像一个漂亮的碗。有的可能看着像洞、山脉、高原或者各种不规则的地形,导致很难收敛到最小值。图4-10显示了梯度下降的两个主要挑战:如果随机初始化,算法从左侧起步,那么会收敛到一个局部最小值,而不是全局最小值。如果算法从右侧起步,那么需要经过很长时间才能越过整片高原,如果你停下得太早,将永远达不到全局最小值。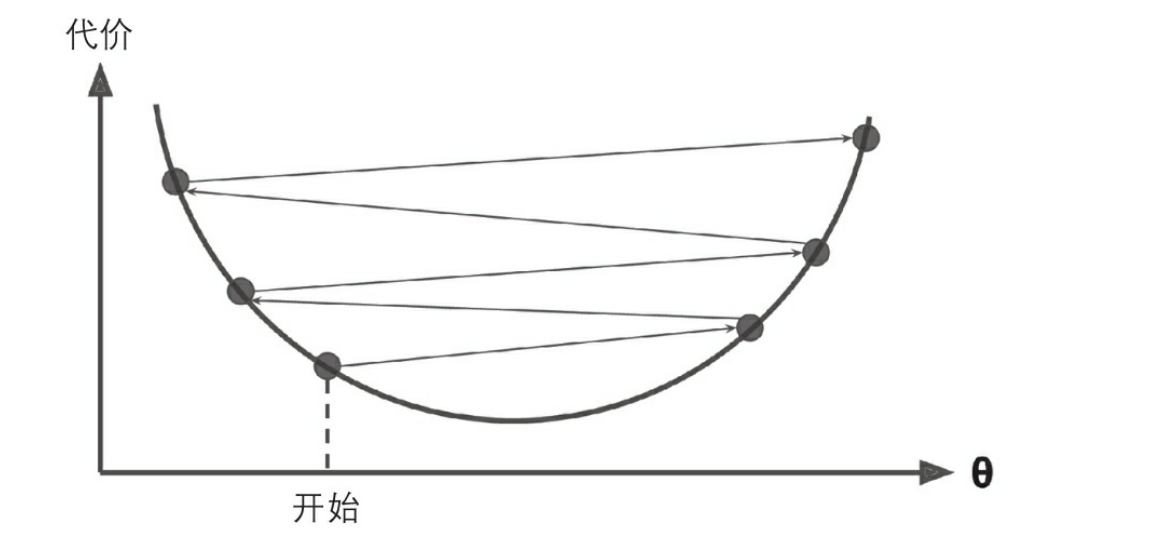
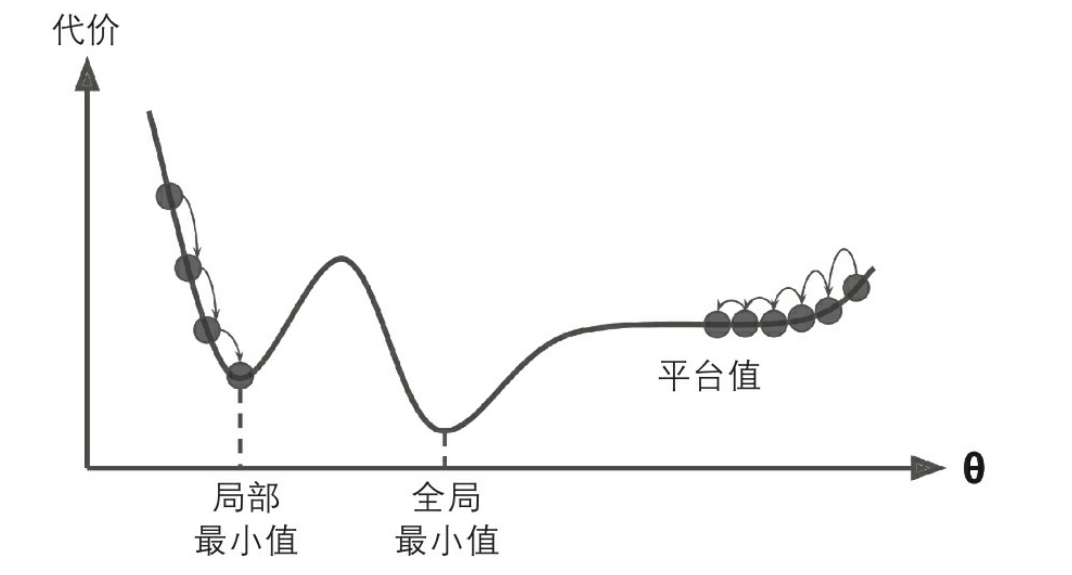
幸好,线性回归模型的MSE成本函数恰好是个凸函数,这意味着连接曲线上任意两点的线段永远不会跟曲线相交。也就是说,不存在局部最小值,只有一个全局最小值。它同时也是一个连续函数,所以斜率不会产生陡峭的变化[1]。这两点保证的结论是:即便是乱走,梯度下降都可以趋近到全局最小值(只要等待时间足够长,学习率也不是太高)。
成本函数虽然是碗状的,但如果不同特征的尺寸差别巨大,那它可能是一个非常细长的碗。如图4-11所示的梯度下降,左边的训练集上特征1和特征2具有相同的数值规模,而右边的训练集上,特征1的值则比特征2要小得多(注:因为特征1的值较小,所以θ1需要更大的变化来影响成本函数,这就是为什么碗形会沿着θ1轴拉长。)。 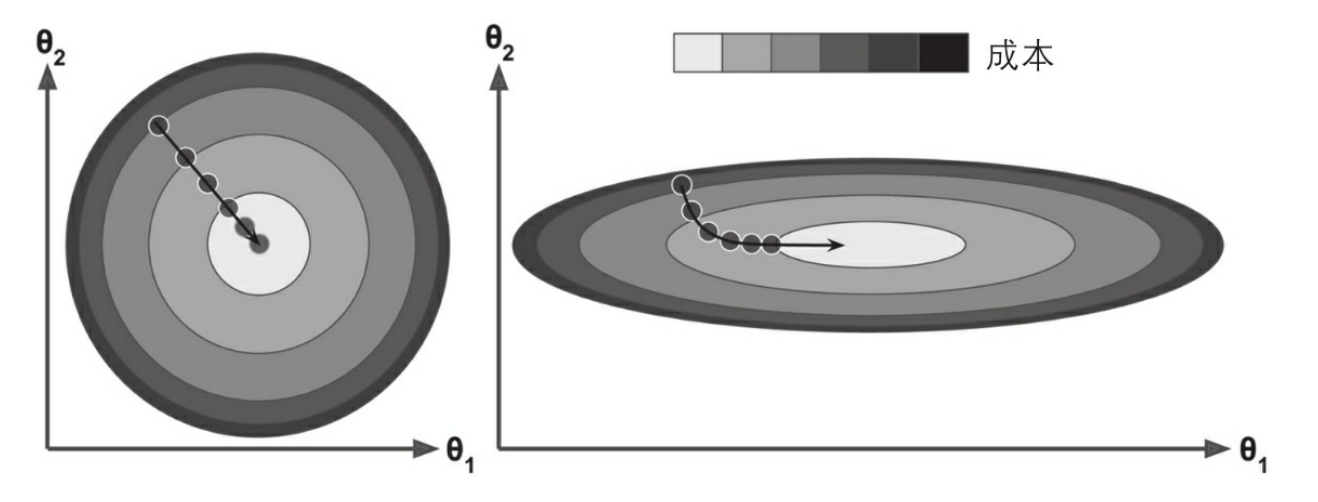
正如你所见,左图的梯度下降算法直接走向最小值,可以快速到达。而在右图中,先是沿着与全局最小值方向近乎垂直的方向前进,接下来是一段几乎平坦的长长的山谷。最终还是会抵达最小值,但是这需要花费大量的时间。
应用梯度下降时,需要保证所有特征值的大小比例都差不多(比如使用Scikit- Learn的StandardScaler类),如图4-11右侧所示,如果某个特征的数据比其他特征大很多,就会导致在进行梯度下降时,在该特征运行很长时间来寻找最短路径,因此收敛的时间就会长很多。
图4-7也说明,训练模型也就是搜寻使成本函数(在训练集上)最小化的参数组合。这是模型参数空间层面上的搜索:模型的参数越多,这个空间的维度就越多,搜索就越难。同样是在干草堆里寻找一根针,在一个三百维的空间里就比在一个三维空间里要棘手得多。幸运的是,线性回归模型的成本函数是凸函数,针就躺在碗底。
4.2.1 批量梯度下降
要实现梯度下降,你需要计算每个模型关于参数θj的成本函数的梯度。换言之,你需要计算的是如果改变θj,成本函数会改变多少。这被称为偏导数。这就好比是在问“如果我面向东,我脚下的坡度斜率是多少?”然后面向北问同样的问题(如果你想象超过三个维度的宇宙,对于其他的维度以此类推)。公式4-5计算了关于参数θj的成本函数的偏导数,计作
公式4-5:损失函数的偏导数:
如果不想单独计算这些偏导数,可以使用公式4-6对其进行一次性计算。梯度向量记作,包含所有成本函数(每个模型参数一个)的偏导数。
公式4-6:损失函数的梯度向量:
请注意,在计算梯度下降的每一步时,都是基于完整的训练集X的。这就是为什么该算法会被称为批量梯度下降:每一步都使用整批训练数据(实际上,全梯度下降可能是个更好的名字)。因此,面对非常庞大的训练集时,算法会变得极慢(不过我们即将看到快得多的梯度下降算法)。但是,梯度下降算法随特征数量扩展的表现比较好。如果要训练的线性模型拥有几十万个特征,使用梯度下降比标准方程或者SVD要快得多。
一旦有了梯度向量,哪个点向上,就朝反方向下坡。也就是从θ中减去这时学习率η就发挥作用了[2]:用梯度向量乘以η确定下坡步长的大小(见公式4-7)。
公式4-7:梯度下降步骤:
让我们看一下该算法的快速实现:
eta = 0.1 # learning raten_iterations = 1000m = 100theta = np.random.randn(2,1) # random initializationfor iteration in range(n_iterations):gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)theta = theta - eta * gradientstheta

嘿,这不正是标准方程的发现么!梯度下降表现完美。如果使用了其他的学习率eta呢?图4-12展现了分别使用三种不同的学习率时,梯度下降的前十步(虚线表示起点)。
左图的学习率太低:算法最终还是能找到解决方法,就是需要太长时间。中间图的学习率看起来非常棒:几次迭代就收敛出了最终解。而右图的学习率太高:算法发散,直接跳过了数据区域,并且每一步都离实际解决方案越来越远。要找到合适的学习率,可以使用网格搜索(见第2章)。但是你可能需要限制迭代次数,这样网格搜索可以淘汰掉那些收敛耗时太长的模型。
你可能会问,要怎么限制迭代次数呢?如果设置太低,算法可能在离最优解还很远时就停了。但是如果设置得太高,模型达到最优解后,继续迭代则参数不再变化,又会浪费时间。一个简单的办法是在开始时设置一个非常大的迭代次数,但是当梯度向量的值变得很微小时中断算法——也就是当它的范数变得低于ε(称为容差)时,因为这时梯度下降已经(几乎)到达了最小值
成本函数为凸函数,并且斜率没有陡峭的变化时(如MSE成本函数),具有固定学习率的批量梯度下降最终会收敛到最佳解,但是你需要等待一段时间:它可以进行O(1/ ε)次迭代以在ε的范围内达到最佳值,具体取决于成本函数的形状。换句话说,如果将容差缩小为原来的1/10(以得到更精确的解),算法将不得不运行10倍的时间。
4.2.2 随机梯度下降
批量梯度下降的主要问题是它要用整个训练集来计算每一步的梯度,所以训练集很大时,算法会特别慢。与之相反的极端是随机梯度下降,每一步在训练集中随机选择一个实例,并且仅基于该单个实例来计算梯度。显然,这让算法变得快多了,因为每次迭代都只需要操作少量的数据。它也可以被用来训练海量的数据集,因为每次迭代只需要在内存中运行一个实例即可(SGD可以作为核外算法实现,见第1章)。
另一方面,由于算法的随机性质,它比批量梯度下降要不规则得多。成本函数将不再是缓缓降低直到抵达最小值,而是不断上上下下,但是从整体来看,还是在慢慢下降。随着时间的推移,最终会非常接近最小值,但是即使它到达了最小值,依旧还会持续反弹,永远不会停止(见图4-13)。所以算法停下来的参数值肯定是足够好的,但不是最优的。 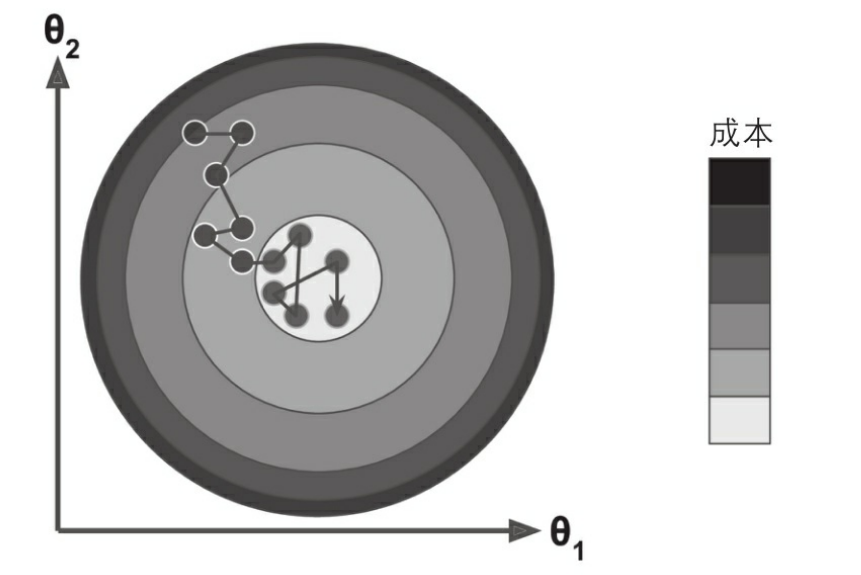
与使用批量梯度下降相比,使用随机梯度下降时,每个训练步骤要快得多,但也更加随机 。当成本函数非常不规则时(见图4-10),随机梯度下降其实可以帮助算法跳出局部最小值,所以相比批量梯度下降,它对找到全局最小值更有优势。
因此,随机性的好处在于可以逃离局部最优,但缺点是永远定位不出最小值。要解决这个困境,有一个办法是逐步降低学习率。开始的步长比较大(这有助于快速进展和逃离局部最小值),然后越来越小,让算法尽量靠近全局最小值。这个过程叫作模拟退火,因为它类似于冶金时熔化的金属慢慢冷却的退火过程。确定每个迭代学习率的函数叫作学习率调度。如果学习率降得太快,可能会陷入局部最小值,甚至是停留在走向最小值的半途中。如果学习率降得太慢,你需要太长时间才能跳到差不多最小值附近,如果提早结束训练,可能只得到一个次优的解决方案。
下面这段代码使用了一个简单的学习率调度实现随机梯度下降:
n_epochs = 50t0, t1 = 5, 50 # learning schedule hyperparametersdef learning_schedule(t):return t0 / (t + t1)theta = np.random.randn(2,1) # random initializationfor epoch in range(n_epochs):for i in range(m):random_index = np.random.randint(m)xi = X_b[random_index:random_index+1]yi = y[random_index:random_index+1]gradients = 2 * xi.T.dot(xi.dot(theta) - yi)eta = learning_schedule(epoch * m + i)theta = theta - eta * gradientstheta
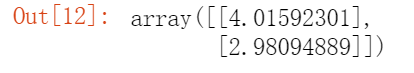
按照惯例,我们进行m个回合的迭代。每个回合称为一个轮次。虽然批量梯度下降代码在整个训练集中进行了1000次迭代,但此代码仅在训练集中遍历了50次,并达到了一个很好的解决方案。
图4-14 显示了训练的前20个步骤(注意这些步骤有多不规则)。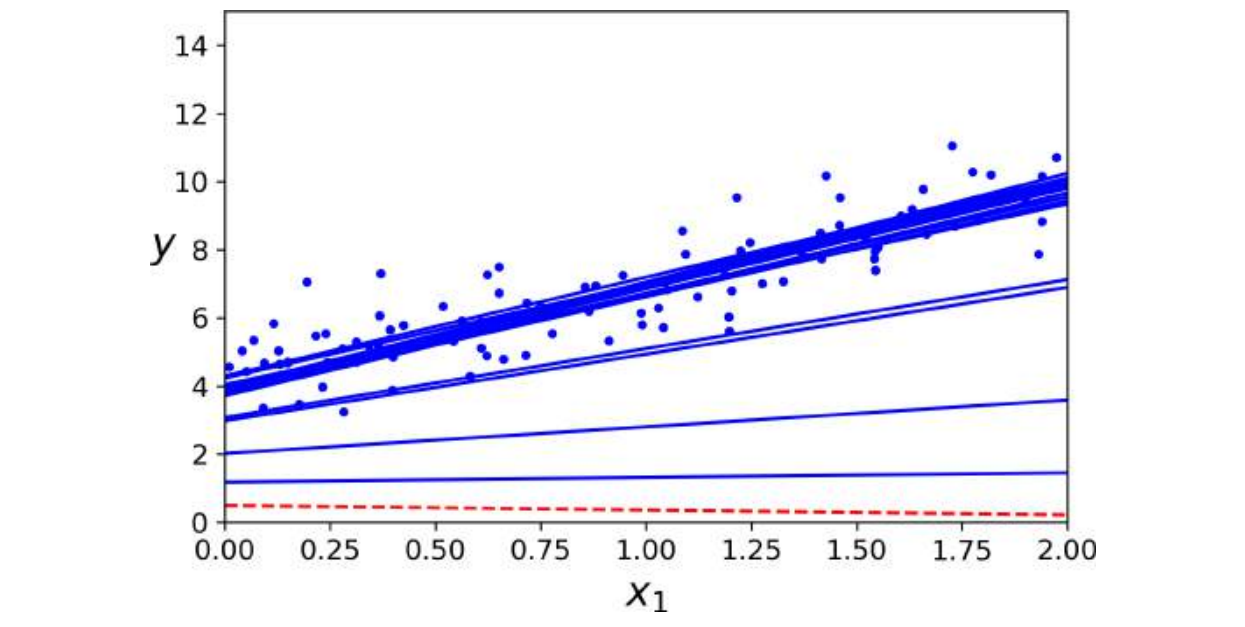
请注意,由于实例是随机选取的,因此某些实例可能每个轮次中被选取几次,而其他实例则可能根本不被选取。如果要确保算法在每个轮次都遍历每个实例,则另一种方法是对训练集进行混洗(确保同时对输入特征和标签进行混洗),然后逐个实例进行遍历,然后对其进行再次混洗,以此类推。但是,这种方法通常收敛较慢。
使用随机梯度下降时,训练实例必须独立且均匀分布(IID),以确保平均而言将参数拉向全局最优值。确保这一点的一种简单方法是在训练过程中对实例进行随机混洗(例如,随机选择每个实例,或者在每个轮次开始时随机混洗训练集)。如果不对实例进行混洗(例如,如果实例按标签排序),那么SGD将首先针对一个标签进行优化,然后针对下一个标签进行优化,以此类推,并且它不会接近全局最小值。
要使用带有Scikit-Learn的随机梯度下降执行线性回归,可以使用SGDRegressor类,该类默认优化平方误差成本函数。以下代码最多可运行1000个轮次,或者直到一个轮次期间损失下降小于0.001为止(max_iter=1000,tol=1e-3)。它使用默认的学习调度(与前一个学习调度不同)以0.1(eta0=0.1)的学习率开始。最后,它不使用任何正则化(penalty=None,稍后将对此进行详细介绍):
from sklearn.linear_model import SGDRegressorsgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)sgd_reg.fit(X, y.ravel())
你再次找到了一种非常接近于由标准方程返回的解:
sgd_reg.intercept_, sgd_reg.coef_
4.3.3 小批量梯度下降
我们要研究的最后一个梯度下降算法称为小批量梯度下降。只要你了解了批量和随机梯度下降,就很容易理解它:在每一步中,不是根据完整的训练集(如批量梯度下降)或仅基于一个实例(如随机梯度下降)来计算梯度,小批量梯度下降在称为小型批量的随机实例集上计算梯度。小批量梯度下降优于随机梯度下降的主要优点是,你可以通过矩阵操作的硬件优化来提高性能,特别是在使用GPU时。
与随机梯度下降相比,该算法在参数空间上的进展更稳定,尤其是在相当大的小批次中。结果,小批量梯度下降最终将比随机梯度下降走得更接近最小值,但它可能很难摆脱局部最小值(在受局部最小值影响的情况下,不像线性回归)。图4-15显示了训练期间参数空间中三种梯度下降算法所采用的路径。它们最终都接近最小值,但是批量梯度下降的路径实际上是在最小值处停止,而随机梯度下降和小批量梯度下降都继续走动。但是,不要忘记批量梯度下降每步需要花费很多时间,如果你使用良好的学习率调度,随机梯度下降和小批量梯度下降也会达到最小值。
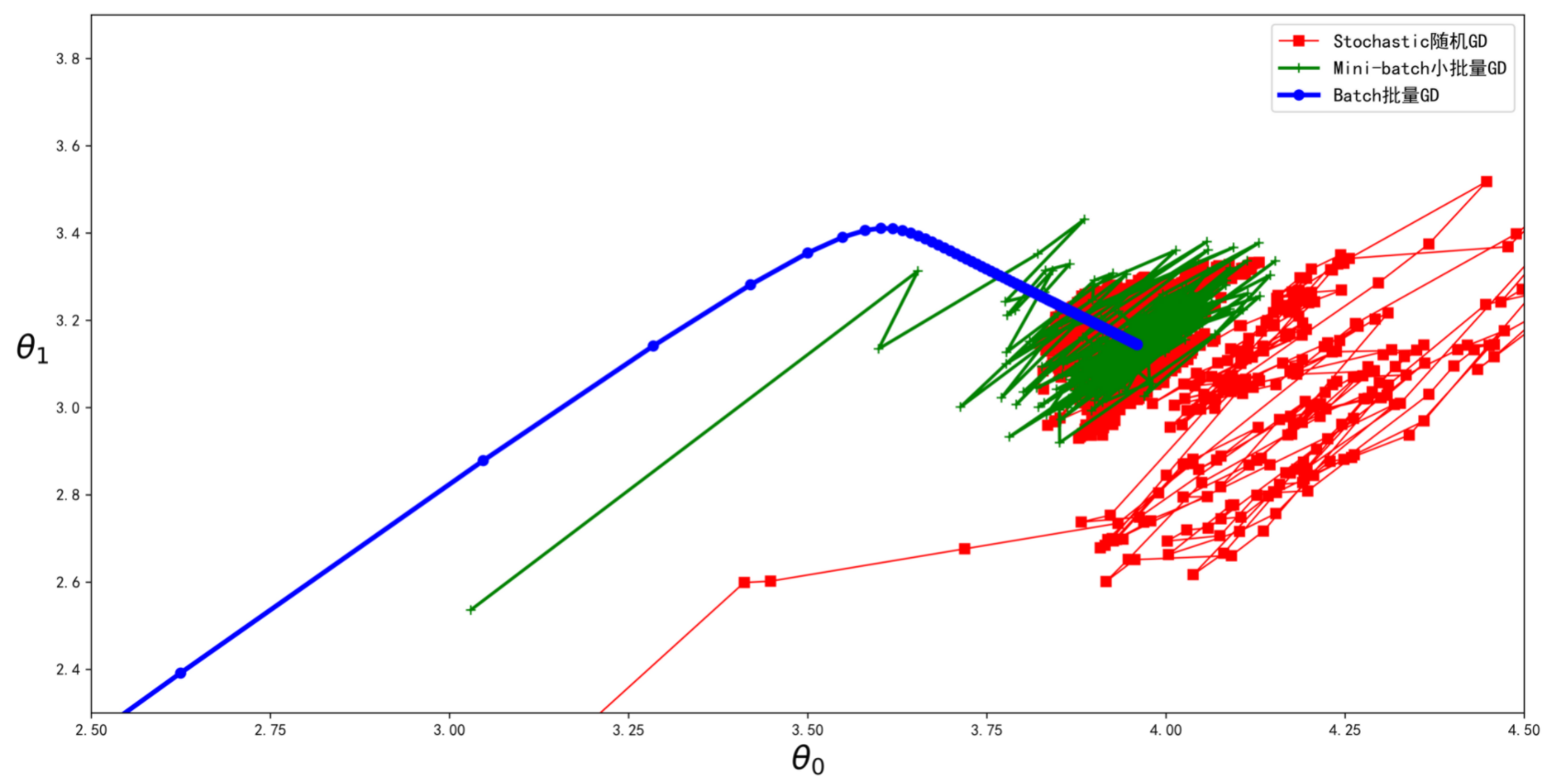
让我们比较到目前为止讨论的线性回归算法[3](回想一下,m是训练实例的数量,n是特征的数量)。请参阅表4-1。
| 算法 | m很大 | 核外支持 | n很大 | 超参数 | 要求缩放 | Scikit-Learn |
|---|---|---|---|---|---|---|
| 标准方程 | 快 | 否 | 慢 | 0 | 否 | N/A |
| SVD | 快 | 否 | 慢 | 0 | 否 | LinerRegression |
| 批量GD | 慢 | 否 | 快 | 2 | 是 | SGDRegressor |
| 随机GD | 快 | 是 | 快 | ≥2 | 是 | SGDRegressor |
| 小批量GD | 快 | 是 | 快 | ≥2 | 是 | SGDRegressor |
训练后几乎没有区别:所有这些算法最终都具有非常相似的模型,并且以完全相同的方式进行预测。
[1] 从技术上讲,它的导数是Lipschitz连续的。
[2] Eta(η)是希腊字母的第7个字母。
[3] 标准方程只能执行线性回归,但可以看到,梯度下降算法可用于训练许多其他模型。
4.3 多项式回归
如果你的数据比直线更复杂怎么办?令人惊讶的是,你可以使用线性模型来拟合非线性数据。一个简单的方法就是将每个特征的幂次方添加为一个新特征,然后在此扩展特征集上训练一个线性模型。这种技术称为多项式回归。
让我们看一个示例。首先,让我们基于一个简单的二次方程式(注:二次方程的形式为y=ax2+bx+c。)(加上一些噪声,见图4-16)生成一些非线性数据:
m = 100X = 6 * np.random.rand(m, 1) - 3y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)plt.figure(dpi=600)plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.axis([-3, 3, 0, 10])plt.rcParams['axes.unicode_minus'] = Falseplt.show()
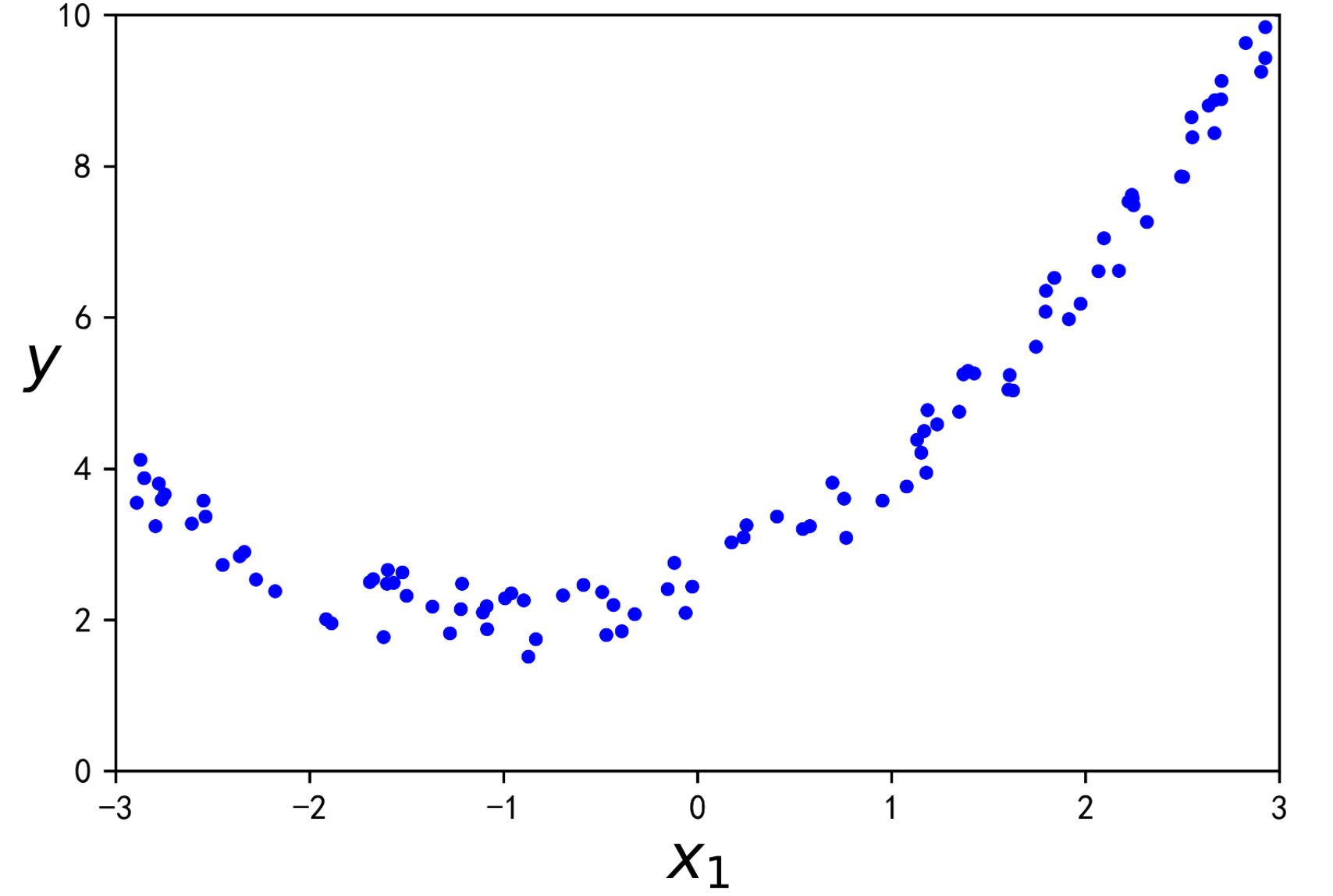
显然,一条直线永远无法正确地拟合此数据。因此,让我们使用Scikit-Learn的PolynomialFeatures类来转换训练数据,将训练集中每个特征的平方(二次多项式)添加为新特征(在这种情况下,只有一个特征):
from sklearn.preprocessing import PolynomialFeaturespoly_features = PolynomialFeatures(degree=2, include_bias=False)X_poly = poly_features.fit_transform(X)X[0]
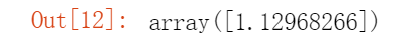
X_poly[0]
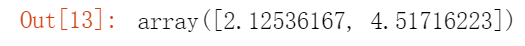
X_poly现在包含X的原始特征以及该特征的平方。现在,你可以将LinearRegression模型拟合到此扩展训练数据中。
lin_reg = LinearRegression()lin_reg.fit(X_poly, y)lin_reg.intercept_, lin_reg.coef_
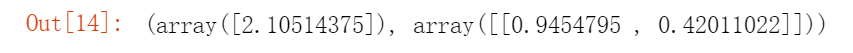
绘制一条曲线来拟合数据:
X_new=np.linspace(-3, 3, 100).reshape(100, 1)X_new_poly = poly_features.transform(X_new)y_new = lin_reg.predict(X_new_poly)plt.figure(dpi=600)plt.plot(X, y, "b.")plt.plot(X_new, y_new, "r-", linewidth=2, label="预测值")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.legend(loc="upper left", fontsize=14)plt.axis([-3, 3, 0, 10])plt.rcParams['axes.unicode_minus'] = Falseplt.show()
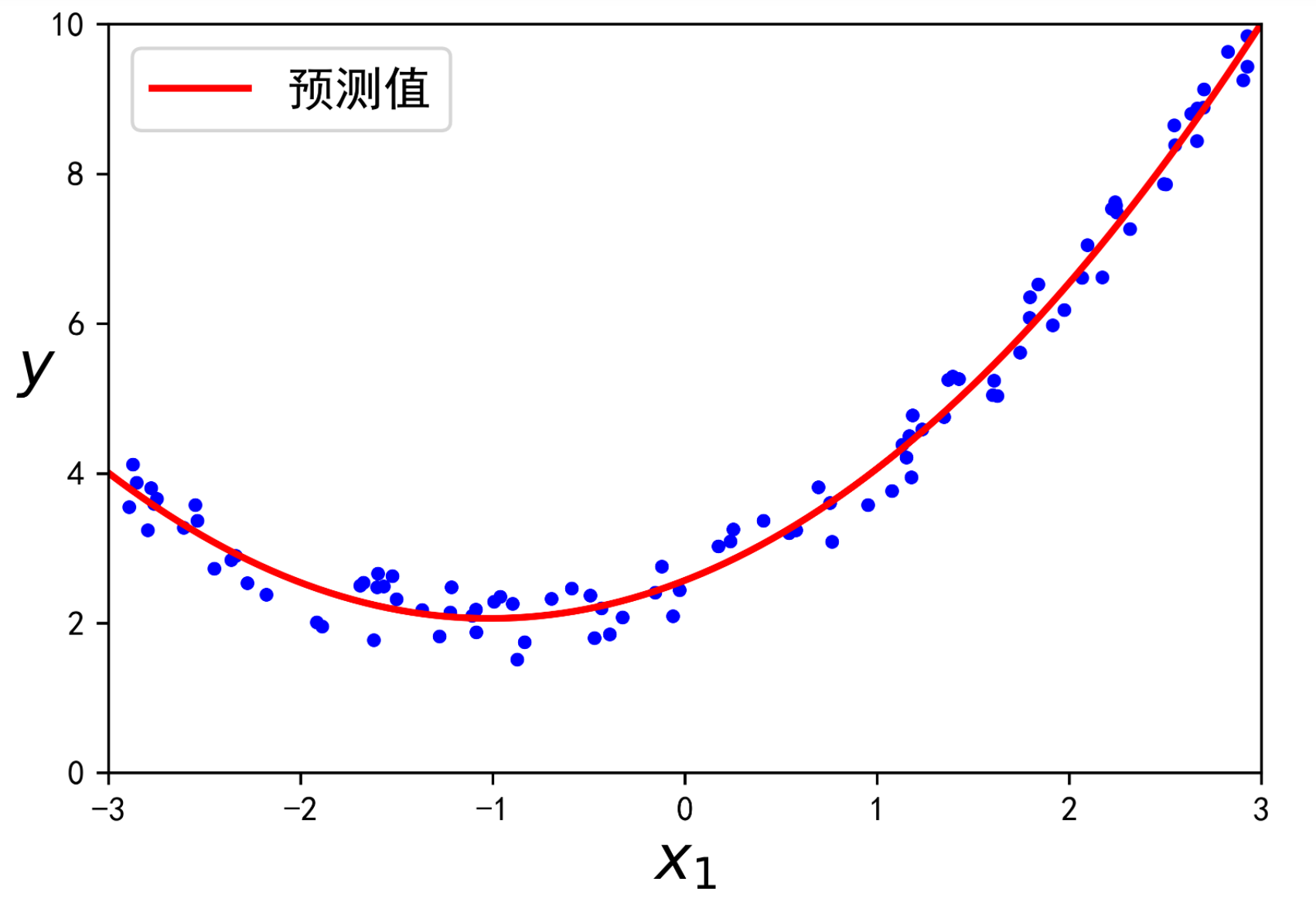
不错:模型估算,而实际上原始函数为
请注意,当存在多个特征时,多项式回归能够找到特征之间的关系(这是普通线性回归模型无法做到的)。PolynomialFeatures还可以将特征的所有组合添加到给定的多项式阶数。例如,如果有两个特征a和b,则degree=3 的PolynomialFeatures不仅会添加特征a2、a3、b2和b3,还会添加组合ab、a2b和ab2。
PolynomialFeatures(degree=d)可以将一个包含n个特征的数组转换为包含
个特征的数组,其中n!是n的阶乘,等于1×2×3×…×n。要小心特征组合的数量爆炸。
4.4 学习曲线
你如果执行高阶多项式回归,与普通线性回归相比,拟合数据可能会更好。例如,图4-18将300阶多项式模型应用于先前的训练数据,将结果与纯线性模型和二次模型(二次多项式)进行比较。请注意300阶多项式模型是如何摆动以尽可能接近训练实例的。 
这种高阶多项式回归模型严重过拟合训练数据,而线性模型则欠拟合。在这种情况下,最能泛化的模型是二次模型,因为数据是使用二次模型生成的。但是总的来说,你不知道数据由什么函数生成,那么如何确定模型的复杂性呢?你如何判断模型是过拟合数据还是欠拟合数据呢?
在第2章中,你使用交叉验证来估计模型的泛化性能。如果模型在训练数据上表现良好,但根据交叉验证的指标泛化较差,则你的模型过拟合。如果两者的表现均不理想,则说明欠拟合。这是一种区别模型是否过于简单或过于复杂的方法。
还有一种方法是观察学习曲线:这个曲线绘制的是模型在训练集和验证集上关于训练集大小(或训练迭代)的性能函数。要生成这个曲线,只需要在不同大小的训练子集上多次训练模型即可。下面这段代码在给定训练集下定义了一个函数,绘制模型的学习曲线:
from sklearn.metrics import mean_squared_errorfrom sklearn.model_selection import train_test_splitdef plot_learning_curves(model, X, y):X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(X_train)):model.fit(X_train[:m], y_train[:m])y_train_predict = model.predict(X_train[:m])y_val_predict = model.predict(X_val)train_errors.append(mean_squared_error(y_train[:m], y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))plt.figure(dpi=400)plt.rc('font',family='SimHei')plt.legend(['训练','验证'])plt.xlabel('训练集大小')plt.ylabel('RMSE')plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
让我们看一下普通线性回归模型的学习曲线(一条直线,见图4-19):
lin_reg = LinearRegression()plot_learning_curves(lin_reg, X, y)plt.legend()plt.ylim([0, 3])
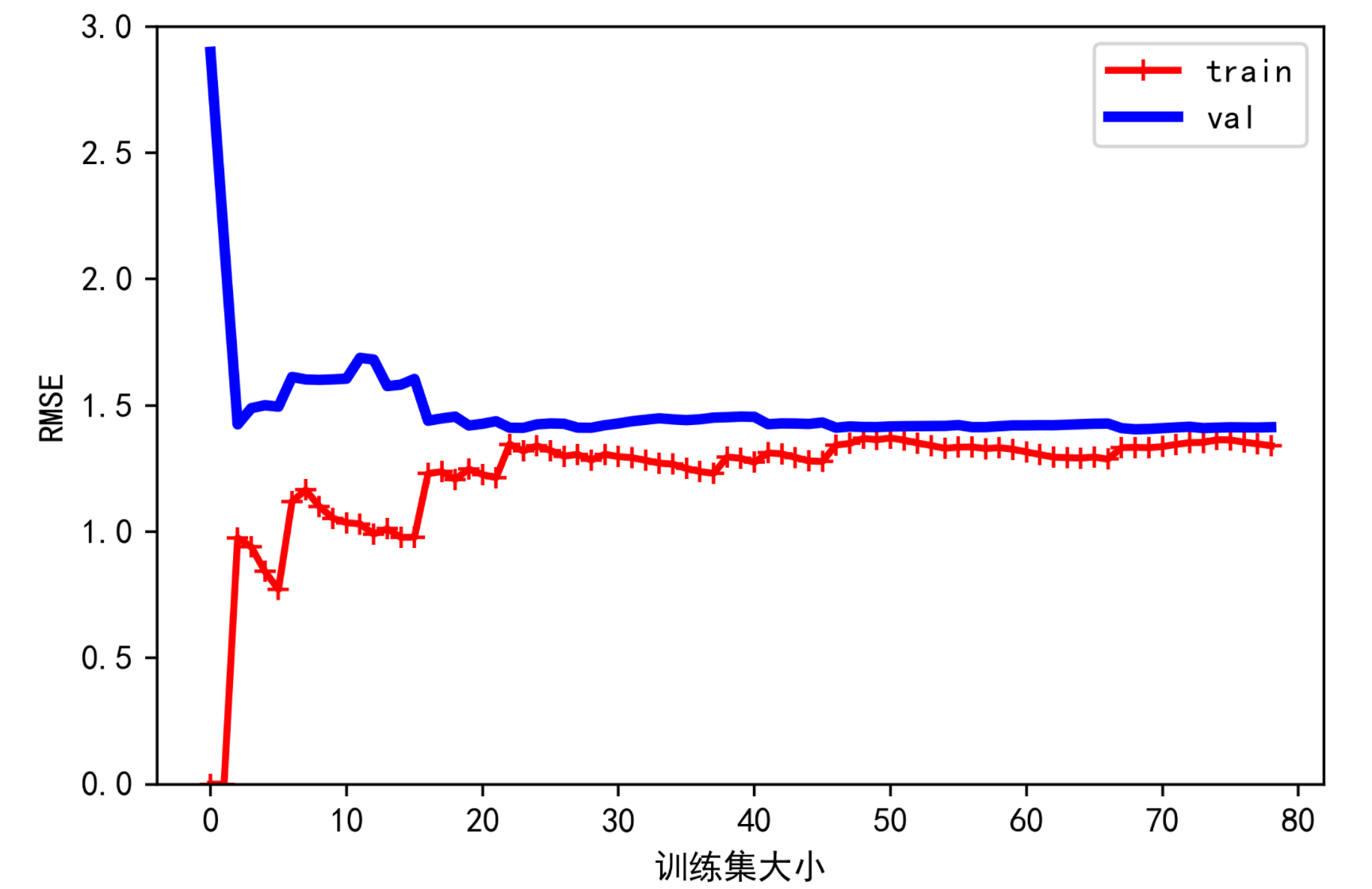
这种欠拟合的模型值得解释一下。首先,让我们看一下在训练数据上的性能:当训练集中只有一个或两个实例时,模型可以很好地拟合它们,这就是曲线从零开始的原因。但是,随着将新实例添加到训练集中,模型就不可能完美地拟合训练数据,这既因为数据有噪声,又因为它根本不是线性的。因此,训练数据上的误差会一直上升,直到达到平稳状态,此时在训练集中添加新实例并不会使平均误差变好或变差。现在让我们看一下模型在验证数据上的性能。当在很少的训练实例上训练模型时,它无法正确泛化,这就是验证误差最初很大的原因。然后,随着模型经历更多的训练示例,它开始学习,因此验证错误逐渐降低。但是,直线不能很好地对数据进行建模,因此误差最终达到一个平稳的状态,非常接近另外一条曲线。
这些学习曲线是典型的欠拟合模型。两条曲线都达到了平稳状态。它们很接近而且很高。
如果你的模型欠拟合训练数据,添加更多训练示例将无济于事。你需要使用更复杂的模型或提供更好的特征。
现在让我们看一下在相同数据上的10阶多项式模型的学习曲线(见图4-20):
from sklearn.pipeline import Pipelinepolynomial_regression = Pipeline([("poly_features", PolynomialFeatures(degree=10, include_bias=False)),("lin_reg", LinearRegression()),])plot_learning_curves(polynomial_regression, X, y)plt.ylim([0, 3])plt.legend()
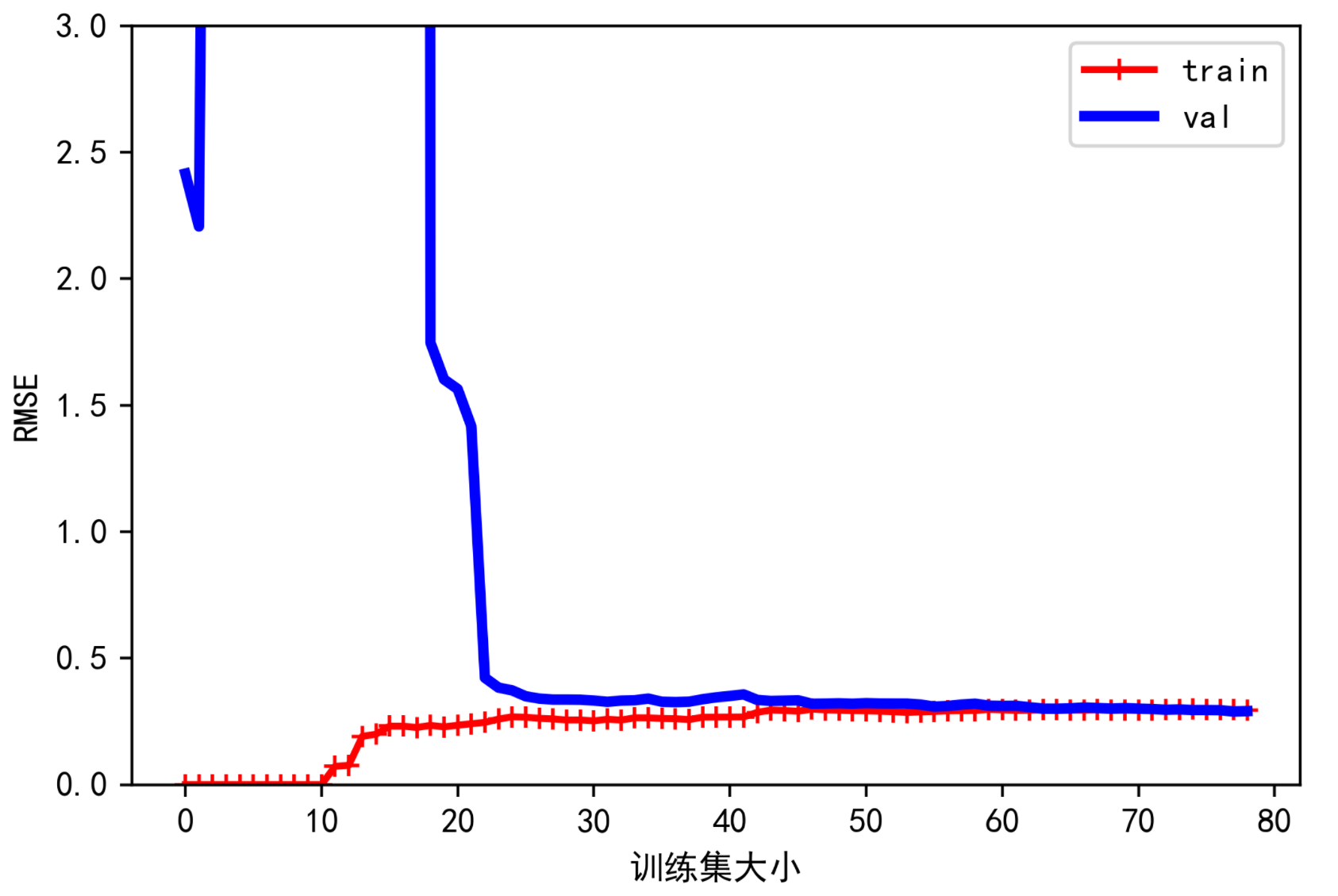
这些学习曲线看起来有点像以前的曲线,但是有两个非常重要的区别:
- 与线性回归模型相比,训练数据上的误差要低得多。
- 曲线之间存在间隙。这意味着该模型在训练数据上的性能要比在验证数据上的性能好得多,这是过拟合模型的标志。但是,如果你使用更大的训练集,则两条曲线会继续接近。
改善过拟合模型的一种方法是向其提供更多的训练数据,直到验证误差达到训练误差为止。
偏差/方差权衡: 统计学和机器学习的重要理论成果是以下事实:模型的泛化误差可以表示为三个非常不同的误差之和:
- 偏差:这部分泛化误差的原因在于错误的假设,比如假设数据是线性的,而实际上是二次的。高偏差模型最有可能欠拟合训练数据[1]。
- 方差:这部分是由于模型对训练数据的细微变化过于敏感。具有许多自由度的模型(例如高阶多项式模型)可能具有较高的方差,因此可能过拟合训练数据。
- 不可避免的误差:这部分误差是因为数据本身的噪声所致。减少这部分误差的唯一方法就是清理数据 (例如修复数据源(如损坏的传感器),或者检测并移除异常值)。
增加模型的复杂度通常会显著提升模型的方差并减少偏差。反过来,降低模型的复杂度则会提升模型的偏差并降低方差。这就是为什么称其为权衡。
[1] 不要将这里的偏差概念与线性模型中的偏置项概念弄混。
4.5 正则化线性模型
正如我们在第1章和第2章中看到的那样,减少过拟合的一个好方法是对模型进行正则化(即约束模型):它拥有的自由度越少,则过拟合数据的难度就越大。正则化多项式模型的一种简单方法是减少多项式的次数。对于线性模型,正则化通常是通过约束模型的权重来实现的。现在,我们看一下岭回归、Lasso回归和弹性网络,它们实现了三种限制权重的方法。
4.5.1 岭回归
岭回归(也称为Tikhonov正则化)是线性回归的正则化版本:将等于的正则化项添加到成本函数。这迫使学习算法不仅拟合数据,而且还使模型权重尽可能小。注意仅在训练期间将正则化项添加到成本函数中。训练完模型后,你要使用非正则化的性能度量来评估模型的性能。
训练过程中使用的成本函数与用于测试的性能指标不同是很常见的。除正则化外,它们可能不同的另一个原因是好的训练成本函数应该具有对优化友好的导数,而用于测试的性能指标应尽可能接近最终目标。例如,通常使用成本函数(例如对数损失(稍后讨论))来训练分类器,但使用精度/召回率对其进行评估。
超参数α控制要对模型进行正则化的程度。如果α=0,则岭回归仅是线性回归。如果α非常大,则所有权重最终都非常接近于零,结果是一条经过数据均值的平线。公式4-8给出了岭回归成本函数[1]。
公式4-8:岭回归成本函数 :
请注意,偏置项θ0没有进行正则化(总和从i=1开始,而不是0)。如果我们将w定义为特征权重的向量(θ1至θn),则正则项等于,其中
表示权重向量的 2范数[2]。对于梯度下降,只需将αw添加到MSE梯度向量(见公式4-6)。
在执行岭回归之前缩放数据(例如使用StandardScaler)很重要,因为它对输入特征的缩放敏感。大多数正则化模型都需要如此。
图4-21显示了使用不同的α值对某些线性数据进行训练的几种岭模型。左侧使用普通岭模型,导致了线性预测。在右侧,首先使用PolynomialFeatures(degree=10)扩展数据,然后使用StandardScaler对其进行缩放,最后将岭模型应用于结果特征:这是带有岭正则化的多项式回归。请注意,α的增加会导致更平坦(即不极端,更合理)的预测,从而减少了模型的方差,但增加了其偏差。
与线性回归一样,我们可以通过计算闭合形式的方程或执行梯度下降来执行岭回归。利弊是相同的。公式4-9显示了闭式解,其中A是(n+1)×(n+1)单位矩阵[3],除了在左上角的单元格中有0(对应于偏置项)。 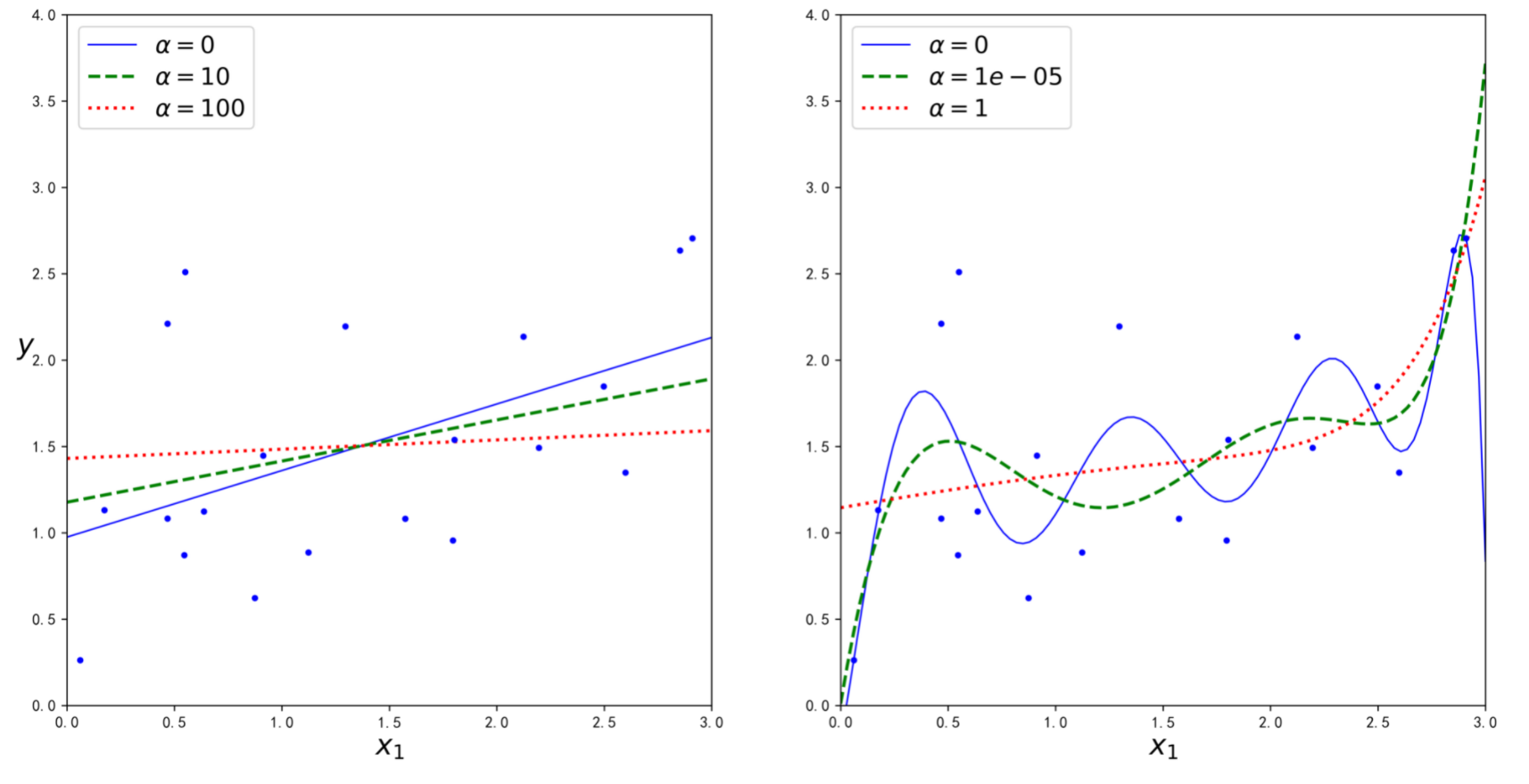
公式4-9:闭式解的岭回归:
以下是用Scikit-Learn和闭式解(方程式4-9正规方程)的一种变体,它使用AndréLouis Cholesky矩阵分解技术)来执行岭回归的方法:
1.首先生成一个横纵坐标范围在[0,3)的随机数,并绘制图像。
np.random.seed(42)m = 20X = 3 * np.random.rand(m, 1)y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5X_new = np.linspace(0, 3, 100).reshape(100, 1)plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.axis([0, 4, 0, 4])plt.figure(figsize=(18, 12),dpi=600)plt.show()
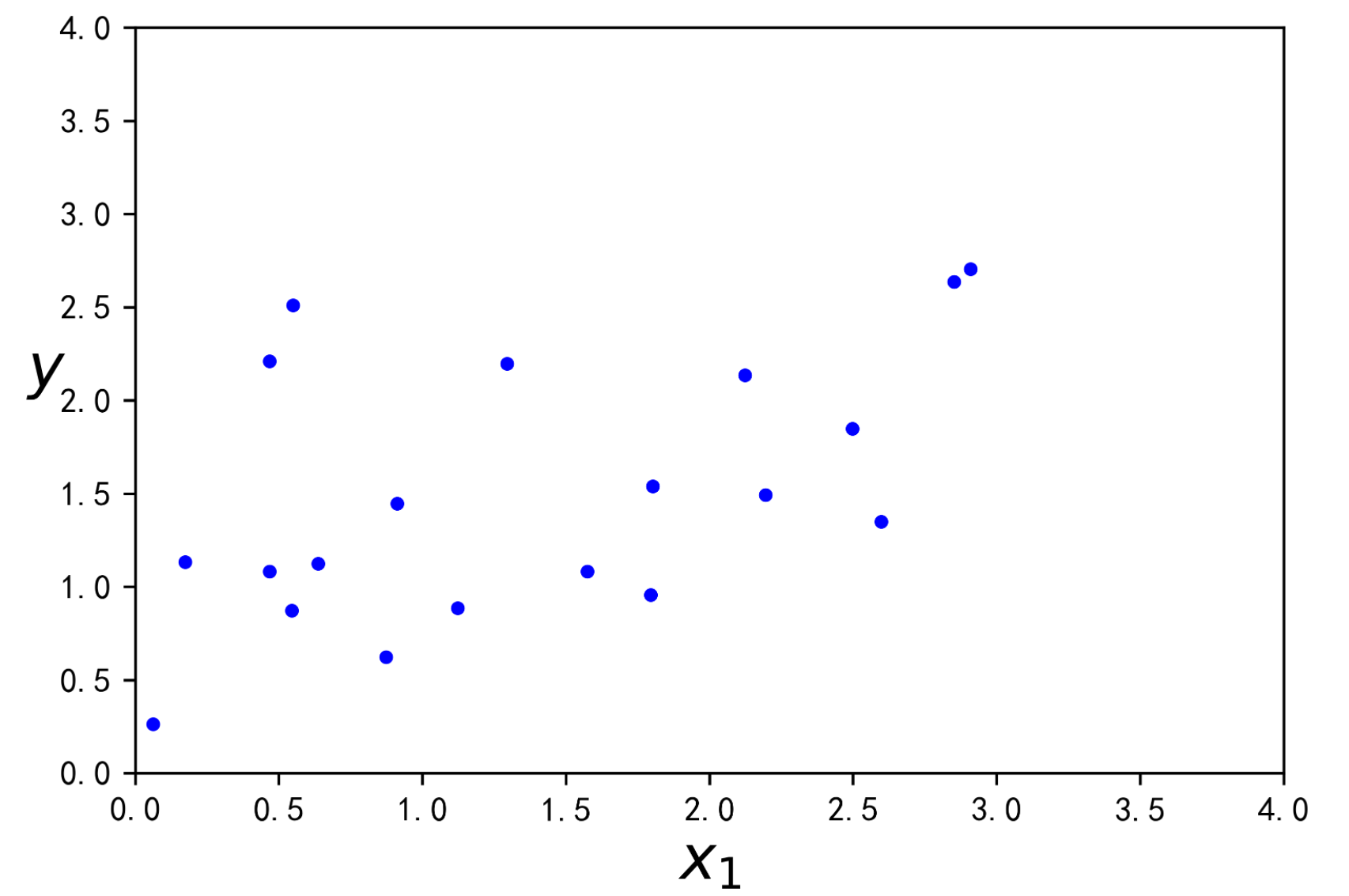
2.训练一个岭回归模型并对X=1.5进行求解预测值。
from sklearn.linear_model import Ridgeridge_reg = Ridge(alpha=1, solver="cholesky")ridge_reg.fit(X, y)ridge_reg.predict([[1.5]])
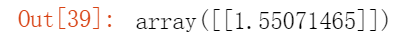
3.并使用随机梯度下降法[4]:
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)ridge_reg.fit(X, y)ridge_reg.predict([[1.5]])

超参数penalty设置的是使用正则项的类型。设为”l2”表示希望SGD在成本函数中添加一个正则项,等于权重向量的 范数的平方的一半,即岭回归。
4.5.2 Lasso回归
线性回归的另一种正则化叫作最小绝对收缩和选择算子回归(Least Absolute Shrinkage and Selection Operator Regression,简称Lasso回归)。与岭回归一样,它也是向成本函数添加一个正则项,但是它增加的是权重向量的范数,而不是
范数的平方的一半(参见公式4-10)。
公式4-10:Lasso回归成本函数:
图4-18显示了与图4-17相同的东西,但是用Lasso模型替换了岭模型,并使用了较小的α值
def plot_model(model_class, polynomial, alphas, **model_kargs):for alpha, style in zip(alphas, ("b-", "g--", "r:")):model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()if polynomial:model = Pipeline([("poly_features", PolynomialFeatures(degree=10, include_bias=False)),("std_scaler", StandardScaler()),("regul_reg", model),])model.fit(X, y)y_new_regul = model.predict(X_new)lw = 2 if alpha > 0 else 1plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))plt.plot(X, y, "b.", linewidth=3)plt.legend(loc="upper left", fontsize=15)plt.xlabel("$x_1$", fontsize=18)plt.axis([0, 3, 0, 4])
from sklearn.linear_model import Lassoplt.figure(figsize=(16,8),dpi=600)plt.subplot(121)plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)plt.ylabel("$y$", rotation=0, fontsize=18)plt.subplot(122)plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)plt.figure(figsize=(18, 12),dpi=600)plt.show()
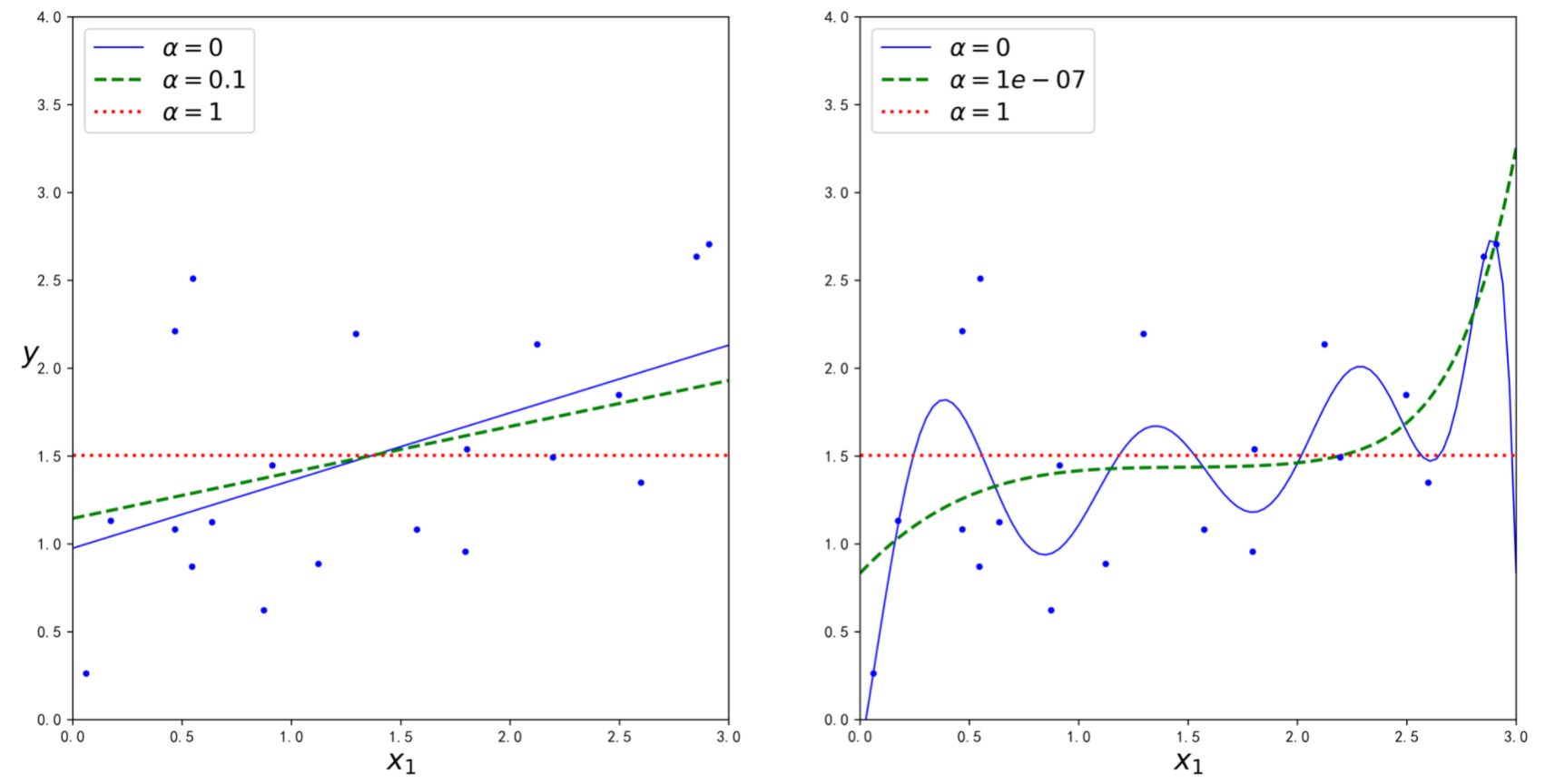
Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重(也就是将它们设置为零)。例如,在图4-23的右图中的虚线(α=10-7)看起来像是二次的,快要接近于线性:因为所有高阶多项式的特征权重都等于零。换句话说,Lasso回归会自动执行特征选择并输出一个稀疏模型(即只有很少的特征有非零权重)。
你可以通过查看图4-24来了解为什么会这样:轴代表两个模型参数,背景轮廓代表不同的损失函数。在左上图中,轮廓线代表损失(|θ1|+|θ2|),当你靠近任何轴时,该损失呈线性下降。例如,如果将模型参数初始化为θ1=2和θ2=0.5,运行梯度下降会使两个参数均等地递减(如黄色虚线所示)。因此θ2将首先达到0(因为开始时接近0)。之后,梯度下降将沿山谷滚动直到其达到θ1=0(有一点反弹,因为
的梯度永远不会接近0:对于每个参数,它们都是-1或1)。在右上方的图中,轮廓线代表Lasso的成本函数(即MSE成本函数加
损失)。白色的小圆圈显示了梯度下降优化某些模型参数的路径,这些参数在θ1=0.25和θ2=-1附近初始化:再次注意该路径如何快速到达θ2=0,然后向下滚动并最终在全局最优值附近反弹(由红色正方形表示)。如果增加α,则全局最优值将沿黄色虚线向左移动;如果减少α,则全局最优值将向右移动(在此示例中,非正则化的MSE的最优参数为θ1=2和θ2=0.5)。
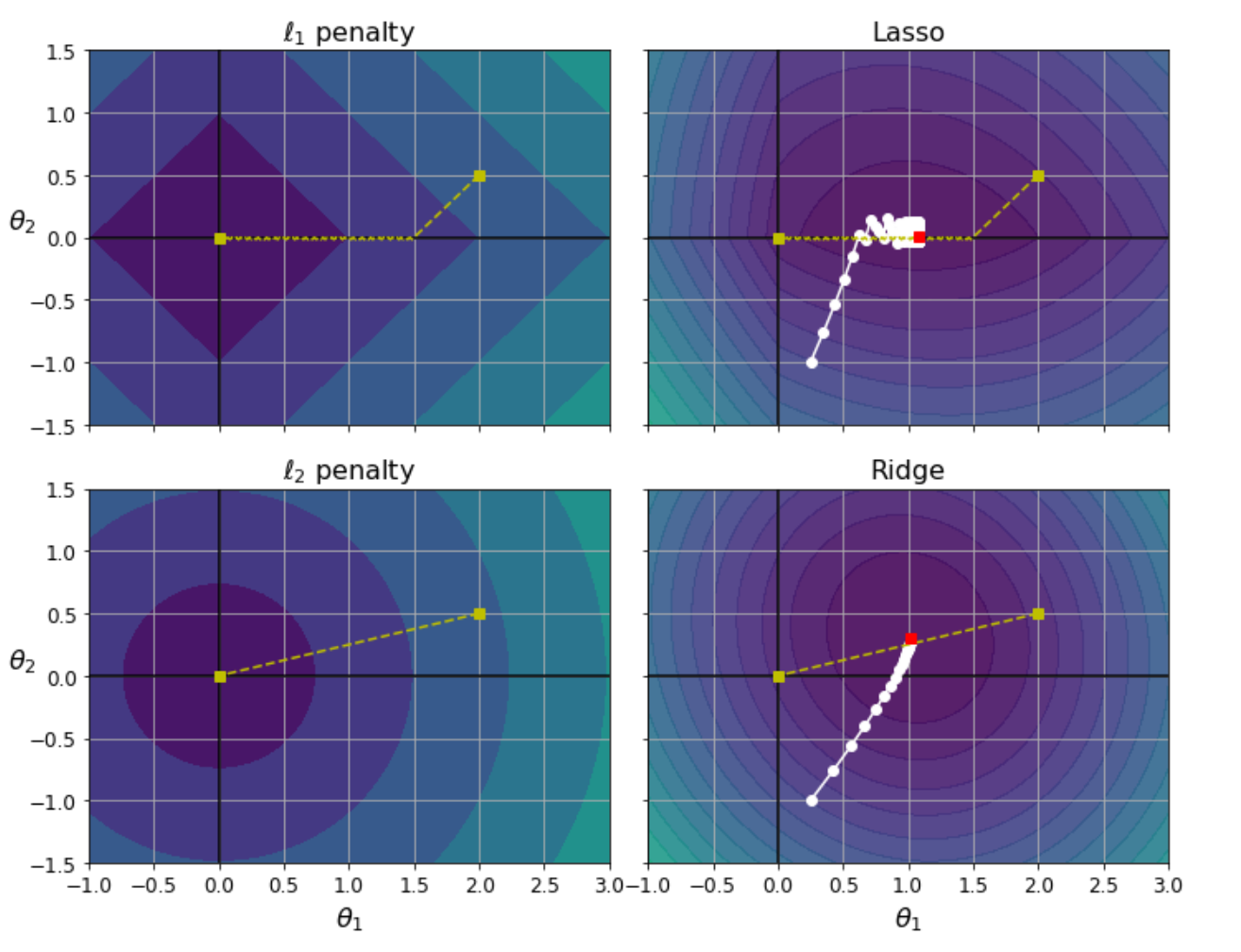
底部的两个图显示了相同的内容,但惩罚为。在左下图中,你可以看到
损失随距原点的距离而减小,因此梯度下降沿该点直走。在右下图中,轮廓线代表岭回归的成本函数(即MSE成本函数加
损失)。Lasso有两个主要区别。
- 首先,随着参数接近全局最优值,梯度会变小,因此,梯度下降自然会减慢,这有助于收敛(因为周围没有反弹)。
- 其次,当你增加α时,最佳参数(用红色正方形表示)越来越接近原点,但是它们从未被完全被消除。
为了避免在使用Lasso时梯度下降最终在最优解附近反弹,你需要逐渐降低训练期间的学习率(它仍然会在最优解附近反弹,但是步长会越来越小,因此会收敛)。
Lasso成本函数在θi=0(对于i=1,2,…,n)处是不可微的,但是如果你使用子梯度向量g[5]代替任何θi=0,则梯度下降仍然可以正常工作。公式4-11显示了可用于带有Lasso成本函数的梯度下降的子梯度向量方程。
公式4-11:Lasso回归子梯度向量:
这是一个使用Lasso类的Scikit-Learn小示例:
请注意,你可以改用SGDRegressor(penalty=”l1”)。
from sklearn.linear_model import Lassolasso_reg = Lasso(alpha=0.1)lasso_reg.fit(X, y)lasso_reg.predict([[1.5]])
4.5.3 弹性网络
弹性网络是介于岭回归和Lasso回归之间的中间地带。正则项是岭和Lasso正则项的简单混合,你可以控制混合比r。当r=0时,弹性网络等效于岭回归,而当r=1时,弹性网络等效于Lasso回归(见公式4-12)。
公式4-12:弹性网络成本函数
那么什么时候应该使用普通的线性回归(即不进行任何正则化)、岭、Lasso或弹性网络呢?通常来说,有正则化——哪怕很小,总比没有更可取一些。所以大多数情况下,你应该避免使用纯线性回归。岭回归是个不错的默认选择,但是如果你觉得实际用到的特征只有少数几个,那就应该更倾向于Lasso回归或是弹性网络,因为它们会将无用特征的权重降为零。一般而言,弹性网络优于Lasso回归,因为当特征数量超过训练实例数量,又或者是几个特征强相关时,Lasso回归的表现可能非常不稳定。
这是一个使用Scikit-Learn的ElasticNet的小示例(l1_ratio对应于混合比r):
from sklearn.linear_model import ElasticNetelastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)elastic_net.fit(X, y)elastic_net.predict([[1.5]])
4.5.4 提前停止
对于梯度下降这一类迭代学习的算法,还有一个与众不同的正则化方法,就是在验证误差达到最小值时停止训练,该方法叫作提前停止法。图4-25展现了一个用批量梯度下降训练的复杂模型(高阶多项式回归模型)。经过一轮一轮的训练,算法不断地学习,训练集上的预测误差(RMSE)自然不断下降,同样其在验证集上的预测误差也随之下降。但是,一段时间之后,验证误差停止下降反而开始回升。这说明模型开始过拟合训练数据。通过早期停止法,一旦验证误差达到最小值就立刻停止训练。这是一个非常简单而有效的正则化技巧,所以Geoffrey Hinton称其为“美丽的免费午餐”。
首先,创造一个带噪声的数据集,并把数据集拆分为训练集和验证集。
np.random.seed(42)m = 100X = 6 * np.random.rand(m, 1) - 3y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(),test_size=0.5, random_state=10)
然后,提前停止法的基本实现:
from copy import deepcopypoly_scaler = Pipeline([("poly_features", PolynomialFeatures(degree=90, include_bias=False)),("std_scaler", StandardScaler())])X_train_poly_scaled = poly_scaler.fit_transform(X_train)X_val_poly_scaled = poly_scaler.transform(X_val)sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)minimum_val_error = float("inf")best_epoch = Nonebest_model = Nonefor epoch in range(1000):sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left offy_val_predict = sgd_reg.predict(X_val_poly_scaled)val_error = mean_squared_error(y_val, y_val_predict)if val_error < minimum_val_error:minimum_val_error = val_errorbest_epoch = epochbest_model = deepcopy(sgd_reg)
请注意,在使用warm_start=True的情况下,当调用fit()方法时,它将在停止的地方继续训练,而不是从头开始。
最后,绘制出图像。
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)n_epochs = 500train_errors, val_errors = [], []for epoch in range(n_epochs):sgd_reg.fit(X_train_poly_scaled, y_train)y_train_predict = sgd_reg.predict(X_train_poly_scaled)y_val_predict = sgd_reg.predict(X_val_poly_scaled)train_errors.append(mean_squared_error(y_train, y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))best_epoch = np.argmin(val_errors)best_val_rmse = np.sqrt(val_errors[best_epoch])plt.figure(dpi=600)plt.annotate('最佳模型',xy=(best_epoch, best_val_rmse),xytext=(best_epoch, best_val_rmse + 1),ha="center",arrowprops=dict(facecolor='black', shrink=0.05),fontsize=16,)best_val_rmse -= 0.03 # just to make the graph look betterplt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="验证集")plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="训练集")plt.legend(loc="upper right", fontsize=14)plt.xlabel("轮次", fontsize=14)plt.ylabel("RMSE", fontsize=14)plt.show()
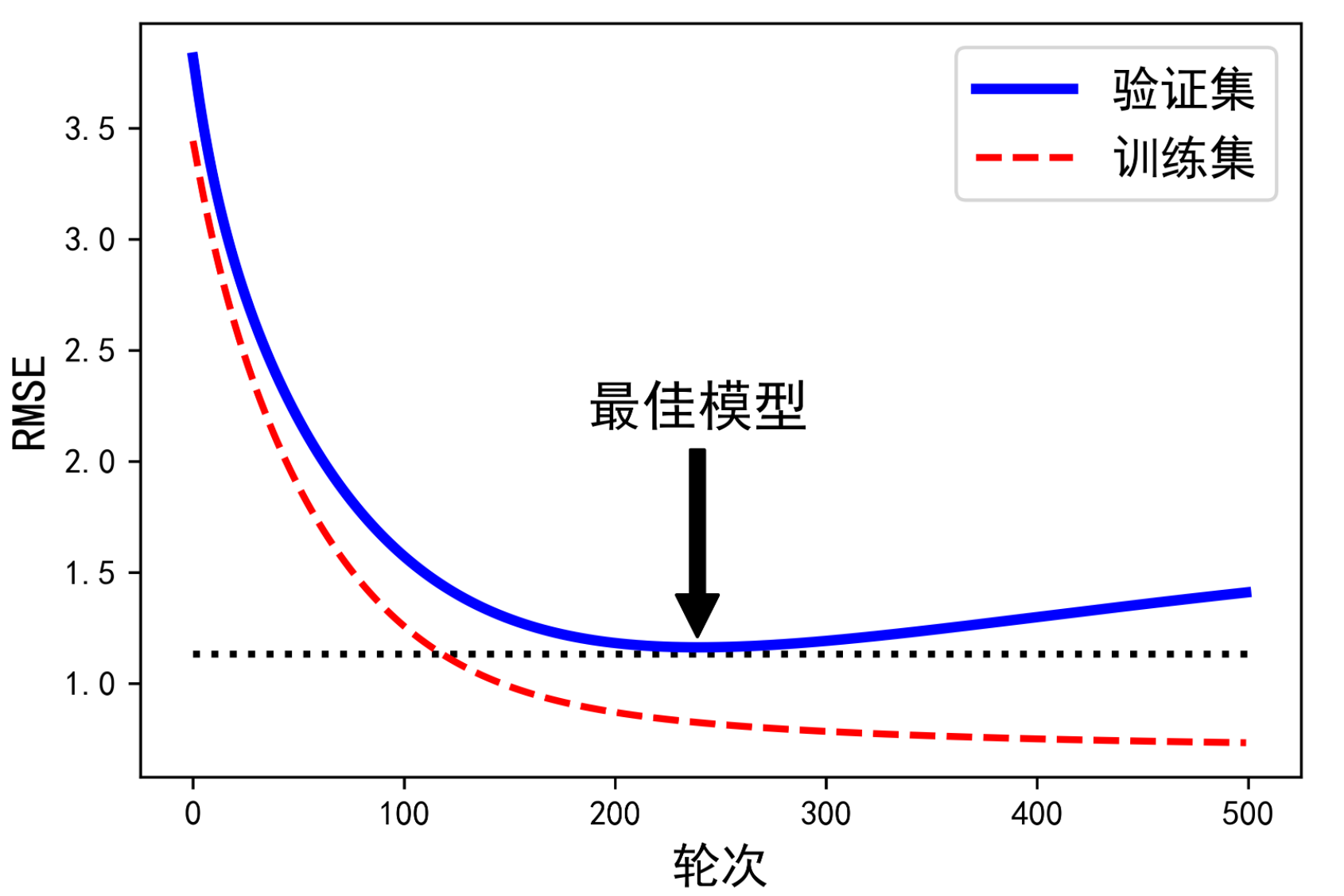
使用随机和小批量梯度下降时,曲线不是那么平滑,可能很难知道你是否达到了最小值。一种解决方案是仅在验证错误超过最小值一段时间后停止(当你确信模型不会做得更好时),然后回滚模型参数到验证误差最小的位置。
[1] 对于没有缩写名称的成本函数,通常使用符号。在本书的其余部分中,我们将经常使用这种表示法。上下文将清楚地说明正在讨论哪个成本函数。
[2] 范数在第2章中讨论。
[3] 除主对角线上的1之外,全为0的方阵(从左上到右下)。
[4] 或者,你可以将Ridge类与”sag”求解器一起使用。随机平均梯度下降是随机梯度下降的变 体。有关更多详细信息,请参阅来自不列颠哥伦比亚大学Mark Schmidt等人的论文 “ Minimizing Finite Sums with the Stochastic Average Gradient Algorithm”。
[5] 你可以将不可微分点处的子梯度向量视为该点周围的梯度向量之间的中间向量。
4.6 逻辑回归
正如第1章中提到过的,一些回归算法也可用于分类(反之亦然)。逻辑回归(Logistic回归,也称为Logit回归)被广泛用于估算一个实例属于某个特定类别的概率。(比如,这封电子邮件属于垃圾邮件的概率是多少?)如果预估概率超过50%,则模型预测该实例属于该类别(称为正类,标记为“1”),反之,则预测不是(称为负类,标记为“0”)。这样它就成了一个二元分类器。
4.6.1 估计概率
所以逻辑回归是怎么工作的呢?与线性回归模型一样,逻辑回归模型也是计算输入特征的加权和(加上偏置项),但是不同于线性回归模型直接输出结果,它输出的是结果的数理逻辑值(参见公式4-13)。
公式4-13:逻辑回归模型的估计概率(向量化形式)
逻辑记为,是一个sigmoid函数(即S型函数),输出一个介于0和1之间的数字。其定义如公式4-14和图4-21所示。
公式4-14:逻辑函数
t = np.linspace(-10, 10, 100)sigmoid = 1 / (1 + np.exp(-t))plt.figure(dpi=600)plt.plot([-10, 10], [0, 0], "k-")plt.plot([-10, 10], [0.5, 0.5], "k:")plt.plot([-10, 10], [1, 1], "k:")plt.plot([0, 0], [-1.1, 1.1], "k-")plt.plot(t, sigmoid, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")plt.xlabel("t")plt.legend(loc="upper left", fontsize=16)plt.axis([-10, 10, -0.1, 1.1])plt.show()
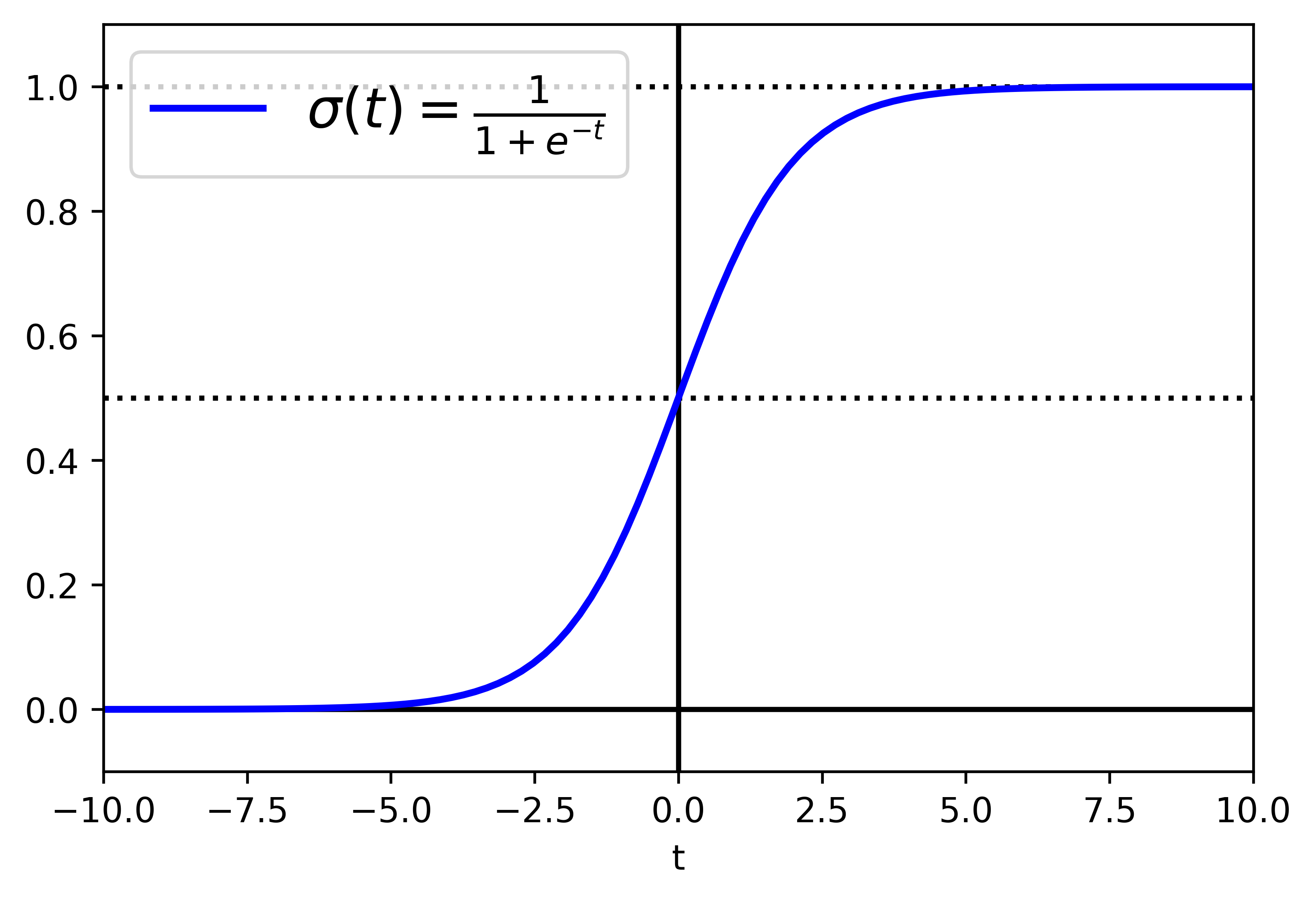
一旦逻辑回归模型估算出实例x属于正类的概率就可以轻松做出预测出
(见公式4-15)。
公式4-15:逻辑回归模型预测
注意,当t<0时,σ(t)<0.5;当t≥0时,σ(t)≥0.5。所以如果xTθ是正类,逻辑回归模型预测结果是1,如果是负类,则预测为0。
分数t通常称为logit。该名称源于以下事实:定义为
的logit函数与logistic函数相反。确实,如果你计算估计概率p的对数,则会发现结果为t。对数也称为对数奇数,因为它是正类别的估计概率与负类别的估计概率之比的对数。
4.6.2 训练和成本函数
现在你知道逻辑回归模型是如何估算概率并做出预测了。但是要怎么训练呢?训练的目的就是设置参数向量θ,使模型对正类实例做出高概率估算(y=1),对负类实例做出低概率估算(y=0)。公式4-16所示为单个训练实例x的成本函数,正说明了这一点。
公式4-16:单个训练实例的成本函数
这个成本函数是有道理的,因为当t接近于0时,-log(t)会变得非常大,所以如果模型估算一个正类实例的概率接近于0,成本将会变得很高。同理估算出一个负类实例的概率接近1,成本也会变得非常高。那么反过来,当t接近于1的时候,-log(t)接近于0,所以对一个负类实例估算出的概率接近于0,对一个正类实例估算出的概率接近于1,而成本则都接近于0,这不正好是我们想要的吗?
整个训练集的成本函数是所有训练实例的平均成本。可以用一个称为对数损失的单一表达式来表示,见公式4-17。
公式4-17:逻辑回归成本函数(对数损失)
但是坏消息是,这个函数没有已知的闭式方程(不存在一个标准方程的等价方程)来计算出最小化成本函数的θ值。而好消息是这是个凸函数,所以通过梯度下降(或是其他任意优化算法)保证能够找出全局最小值(只要学习率不是太高,你又能长时间等待)。公式4-18给出了成本函数关于第j个模型参数θj的偏导数方程。
公式4-18:逻辑成本函数偏导数
该公式与公式4-5非常相似:对于每个实例,它都会计算预测误差并将其乘以第j个特征值,然后计算所有训练实例的平均值。一旦你有了包含所有偏导数的梯度向量就可以使用梯度下降算法了。就是这样,现在你知道如何训练逻辑模型了。对于随机梯度下降,一次使用一个实例;对于小批量梯度下降,一次使用一个小批量。
4.6.3 决策边界
这里我们用鸢尾植物数据集来说明逻辑回归。这是一个非常著名的数据集Iris数据集,共有150朵鸢尾花,分别来自三个不同品种(山鸢尾、变色鸢尾和维吉尼亚鸢尾),数据里包含花的萼片以及花瓣的长度和宽度(见图4-22)。 ![4-22 三种不同品种的鸢尾花[1] image.png](/uploads/projects/shekonghuanzheyanglaoshi@gfys4s/535626522920771ecf992b851b186ab5.png)
我们试试仅基于花瓣宽度这一个特征,创建一个分类器来检测维吉尼亚鸢尾花。首先加载数据:
from sklearn import datasetsiris = datasets.load_iris()list(iris.keys())

X = iris["data"][:, 3:] # petal widthy = (iris["target"] == 2).astype(np.int) # 1 if Iris virginica, else 0
训练一个逻辑回归模型:
from sklearn.linear_model import LogisticRegressionlog_reg = LogisticRegression(solver="lbfgs", random_state=42)log_reg.fit(X, y)
我们来看看花瓣宽度在0到3cm之间的鸢尾花,模型估算出的概率(见图4-23)[2]:
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)y_proba = log_reg.predict_proba(X_new)decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]plt.figure(dpi=600)plt.rc('font',family='SimHei')plt.rcParams['axes.unicode_minus'] = Falseplt.plot(X[y==0], y[y==0], "bs")plt.plot(X[y==1], y[y==1], "g^")plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="维吉尼亚鸢尾花")plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="非维吉尼亚鸢尾花")plt.text(decision_boundary+0.02, 0.15, "决策边界", fontsize=14, color="k", ha="center")plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')plt.xlabel("花瓣宽度 (cm)", fontsize=14)plt.ylabel("概率", fontsize=14)plt.legend(loc="center left", fontsize=14)plt.axis([0, 3, -0.02, 1.02])plt.show()

维吉尼亚鸢尾(三角形所示)的花瓣宽度范围为1.4~2.5cm,而其他两种鸢尾花(正方形所示)花瓣通常较窄,花瓣宽度范围为0.1~1.8cm。注意,这里有一部分重叠。对花瓣宽度超过2cm的花,分类器可以很有信心地说它是一朵维吉尼亚鸢尾花(对该类别输出一个高概率值),对花瓣宽度低于1cm以下的,也可以胸有成竹地说其不是(对“非维吉尼亚鸢尾”类别输出一个高概率值)。在这两个极端之间,分类器则不太有把握。但是,如果你要求它预测出类别(使用predict()方法而不是predict_proba()方法),它将返回一个可能性最大的类别。也就是说,在大约1.6cm处存在一个决策边界,这里“是”和“不是”的可能性都是50%,如果花瓣宽度大于1.6cm,分类器就预测它是维吉尼亚鸢尾花,否则就预测不是(即使它没什么把握):
log_reg.predict([[1.7], [1.5]])
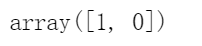
图4-24还是同样的数据集,但是这次显示了两个特征:花瓣宽度和花瓣长度。经过训练,这个逻辑回归分类器就可以基于这两个特征来预测新花朵是否属于维吉尼亚鸢尾。虚线表示模型估算概率为50%的点,即模型的决策边界。注意这里是一个线性的边界(注: 这是点x的集合,使得θ0+θ1x1+θ2x2=0,它定义了一条直线。)。每条平行线都分别代表一个模型输出的特定概率,从左下的15%到右上的90%。根据这个模型,右上线之上的所有花朵都有超过90%的概率属于维吉尼亚鸢尾。
与其他线性模型一样,逻辑回归模型可以用或
惩罚函数来正则化。Scikit-Learn默认添加的是
函数。
控制Scikit-Learn LogisticRegression模型的正则化强度的超参数不是alpha(与其他 线性模型一样),而是反值C。C值越高,对模型的正则化越少。
4.6.4 Softmax回归
逻辑回归模型经过推广,可以直接支持多个类别,而不需要训练并组合多个二元分类器(如第3章所述)。这就是Softmax回归,或者叫作多元逻辑回归。
原理很简单:给定一个实例x,Softmax回归模型首先计算出每个类k的分数sk(x),然后对这些分数应用softmax函数(也叫归一化指数),估算出每个类的概率。你应该很熟悉计算sk(x)分数的公式(见公式4-19),因为它看起来就跟线性回归预测的方程一样。
公式4-19:类k的Softmax分数
请注意,每个类都有自己的特定参数向量θ(x)。所有这些向量通常都作为行存储在参数矩阵Θ中。
一旦为实例x计算了每个类的分数,就可以通过softmax函数来估计实例属于类k的概率(见公式4-20)。该函数计算每个分数的指数,然后对其进行归一化(除以所有指数的总和)。分数通常称为对数或对数奇数(尽管它们实际上是未归一化的对数奇数)。
公式4-20:Softmax函数
在此等式中:
- K是类数。
- s(x)是一个向量,其中包含实例x的每个类的分数。
- σ(s(x))k是实例x属于类k的估计概率,给定该实例每个类的分数。
就像逻辑回归分类器一样,Softmax回归分类器预测具有最高估计概率的类(简单来说就是得分最高的类),如公式4-21所示。
公式4-21:Softmax回归分类预测
argmax运算符返回使函数最大化的变量值。在此等式中,它返回使估计概率 σ(s(x))k最大化的k值。
Softmax回归分类器一次只能预测一个类(即它是多类,而不是多输出),因此它只能与互斥的类(例如不同类型的植物)一起使用。你无法使用它在一张照片中识别多个人。
既然你已经知道了模型如何进行概率估算并做出预测,那我们再来看看怎么训练。训练目标是得到一个能对目标类做出高概率估算的模型(也就是其他类的概率相应要很低)。通过将公式4-22的成本函数(也叫作交叉熵)最小化来实现这个目标,因为当模型对目标类做出较低概率的估算时会受到惩罚。交叉熵经常被用于衡量一组估算出的类概率跟目标类的匹配程度(后面的章节中还会多次用到)。
公式4-22:交叉熵成本函数
在此等式中:
· 是属于类k的第i个实例的目标概率。一般而言等于1或0,具体取决于实例是否属于该类请注意,当只有两个类(K=2)时,此成本函数等效于逻辑回归的成本函数(对数损失,请参见公式4-17)。
交叉熵: 交叉熵源于信息理论。假设你想要有效传递每天的天气信息,选项(晴、下雨等)有8个,那么你可以用3比特对每个选项进行编码,因为23=8。但是,如果你认为几乎每天都是晴天,那么,对“晴天”用1比特(0),其他7个类用4比特(从1开始)进行编码,显然会更有效率一些。交叉熵测量的是你每次发送天气选项的平均比特数。如果你对天气的假设是完美的,交叉熵将会等于天气本身的熵(也就是其本身固有的不可预测性)。但是如果你的假设是错误的(比如经常下雨),交叉熵将会变大,增加的这一部分我们称之为KL散度(Kullback-Leibler divergence,也叫作相对熵)。
两个概率分布p和q之间的交叉熵定义为H(p,q)=-∑x p(x) logqp(x)(至少在离散分布时可以这样定义)。
公式(4-23)给出了该成本函数相对于θ(k)的梯度向量。
公式4-23:类k的交叉熵梯度向量
现在,你可以计算每个类的梯度向量,然后使用梯度下降(或任何其他优化算法)来找到最小化成本函数的参数矩阵
我们来使用Softmax回归将鸢尾花分为三类。当用两个以上的类训练时,Scikit-Learn 的LogisticRegressio默认选择使用的是一对多的训练方式,不过将超参数multiclass设置为”multinomial”,可以将其切换成Softmax回归。你还必须指定一个支持Softmax回归的求解器,比如”lbfgs”求解器(详见Scikit-Learn文档)。默认使用正则化,你可以通过超参数C进行控制:
X = iris["data"][:, (2, 3)] # petal length, petal widthy = iris["target"]softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)softmax_reg.fit(X, y)
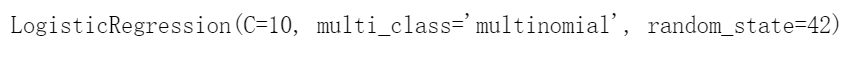
所以当你下次碰到一朵鸢尾花,花瓣长5cm宽2cm,你就可以让模型告诉你它的种类,它会回答说:94.2%的概率是维吉尼亚鸢尾(第2类)或者5.8%的概率为变色鸢尾:
softmax_reg.predict([[5, 2]])
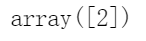
softmax_reg.predict_proba([[5, 2]])
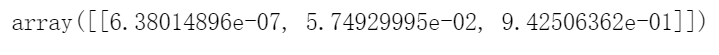
图4-25展现了由不同背景色表示的决策边界。注意,任何两个类之间的决策边界都是线性的。图中的折线表示属于变色鸢尾的概率(例如,标记为0.45的线代表45%的概率边界)。注意,该模型预测出的类,其估算概率有可能低于50%,比如,在所有决策边界相交的地方,所有类的估算概率都为33%。 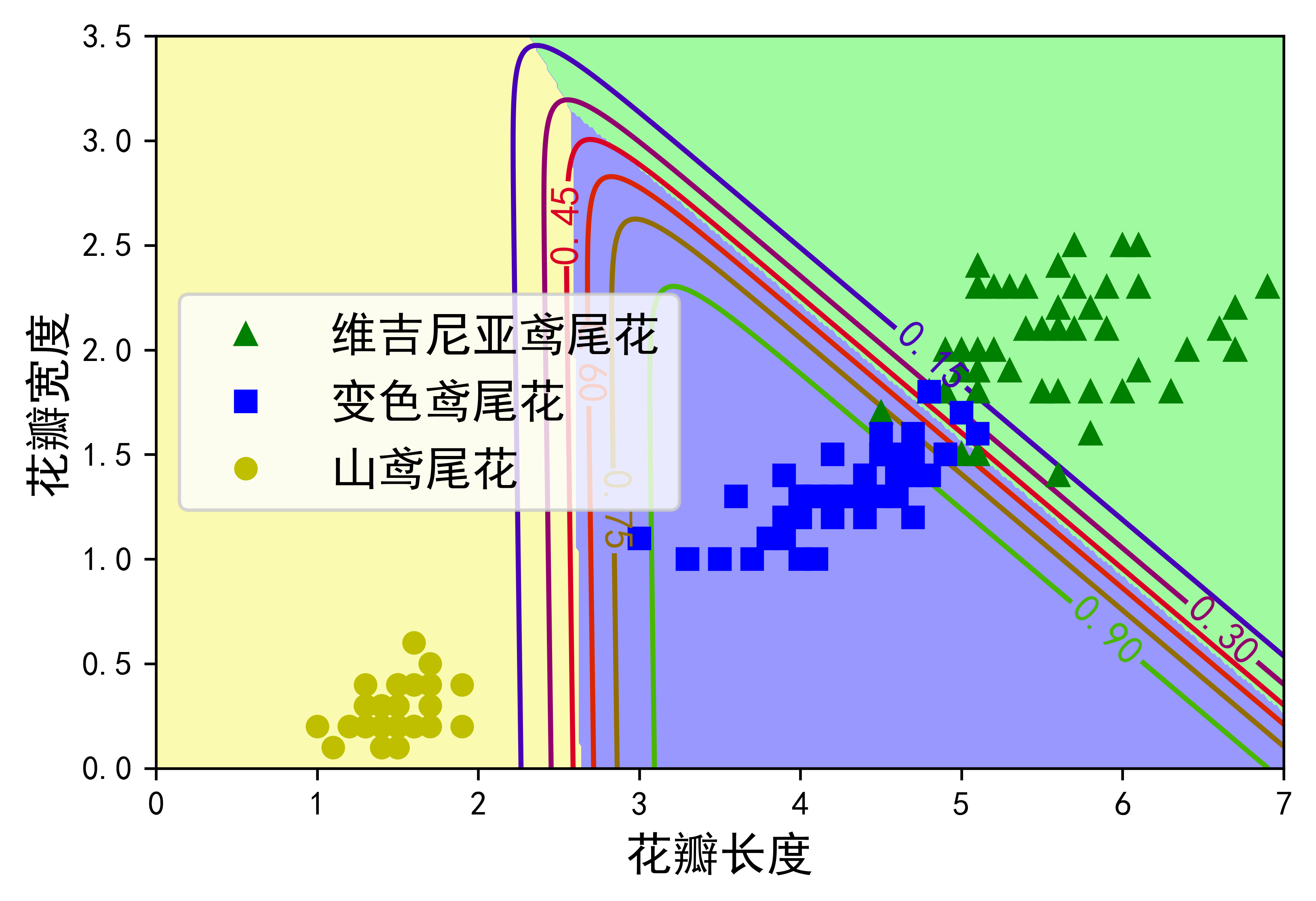
[1] 图片转自相应的维基百科页面。维吉尼亚鸢尾花的图片出自Frank Mayfield,变色鸢尾花的图片出自D.Gordon E.Robertson(Creative Commons BY-SA 3.0),山鸢尾花图片来自公共域。
[2] NumPy的reshape()函数允许将一个维度设为“-1”,这意味着“未指定”:该值是从数组的长度和其余维度推断出来的。
4.7 练习题
- 如果训练集具有数百万个特征,那么可以使用哪种线性回归训练算法?
- 如果训练集里特征的数值大小迥异,哪种算法可能会受到影响?受影响程度如何?你应该怎么做?
- 训练逻辑回归模型时,梯度下降会卡在局部最小值中吗?
- 如果你让它们运行足够长的时间,是否所有的梯度下降算法都能得出相同的模型?
- 假设你使用批量梯度下降,并在每个轮次绘制验证误差。如果你发现验证错误持续上升,可 能是什么情况?你该如何解决?
- 当验证错误上升时立即停止小批量梯度下降是个好主意吗?
- 哪种梯度下降算法(在我们讨论过的算法中)将最快到达最佳解附近?哪个实际上会收敛?如何使其他的也收敛?
- 假设你正在使用多项式回归。绘制学习曲线后,你会发现训练误差和验证误差之间存在很大的差距。发生了什么?解决此问题的三种方法是什么?
- 假设你正在使用岭回归,并且你注意到训练误差和验证误差几乎相等且相当高。你是否会说模型存在高偏差或高方差?你应该增加正则化超参数α还是减小它呢?
- 为什么要使用:
a.岭回归而不是简单的线性回归(即没有任何正则化)?
b.Lasso而不是岭回归?
c.弹性网络而不是Lasso?
- 假设你要将图片分类为室外/室内和白天/夜间。你应该实现两个逻辑回归分类器还是一个 Softmax回归分类器?
- 用Softmax回归进行批量梯度下降训练,实现提前停止法(不使用Scikit-Learn)。