贝叶斯方法

朴素贝叶斯法（Naive Bayes）是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入 x ，利用贝叶斯定理求出后验概率最大的输出 y ，即为对应的类别。
在夏季，某公园男性穿凉鞋的概率为 1/2 ，女性穿凉鞋的概率为 2/3 ，并且该公园中男女比例通常为 2:1 ，问题：若你在公园中随机遇到一个穿凉鞋的人，请问他的性别为男性或女性的概率分别为多少？

先验概率

以上题为例，来解释一下什么是先验概率。假设某公园中一个人是男性为事件 Y=男 ,是女性则是 Y=女 ；一个人穿凉鞋为事件 X=凉鞋 ，未穿凉鞋为事件 X=非凉鞋 。而一个人的性别与是否穿凉鞋这两个事件之间是相互独立的。于是我们可以看到该例子中存在四个先验概率：

先验概率是指根据以往经验和分析得到的概率，上述的4个先验概率即为在未开始试验之前，事件发生的概率。由于男女生的比例是2:1，那么P(Y=男)自然等于2/3，P(Y=女)同理。而先验概率P(X=凉鞋)与P(X=非凉鞋) 并不能直接得出，需要根据全概率公式来求解。在学习全概率公式之前，我们先了解一下条件概率。

条件概率

一个事件发生后另一个事件发生的概率。一般的形式为P(x|y)表示已知事件y发生的条件下x发生的概率。设x，y为随机事件，且P(y)＞0，则有条件概率：
公式一：。
其中 P(xy) 是联合概率，也就是x和y两个事件共同发生的概率。而 P(y)以及P(x) 是先验概率。我们用例子来说明一下就是：“某公园男性穿凉鞋的概率为 1/2 ”，也就是说“是男性的前提下，穿凉鞋的概率是 1/2 ”，此概率为条件概率，即 P(X=凉鞋|Y=男)=1/2 。同理“女性穿凉鞋的概率为 2/3 ” 为条件概率 P(X=凉鞋|Y=女)=1/2 。

全概率公式

根据条件概率中的定义，P(X|Y)是事件Y发生的条件下事件X发生的概率，通常它不会等于P(X)——这比较好理解。而P(X|Y)=P(Y)，说明事件Y对事件X没有任何影响。像这样的两个事件X与Y， 则称之为相互独立的。
而在条件概率中联合事件概率P(XY)=P(X)P(Y)也是对两个事件相互独立的定义，并且是更普遍的判断方法，因为用这个式子不需要考虑P(Y)是否为0的情况了。因此如果我们把 P(XY)=P(X)P(Y)式推广到n个相互对立的事件，设事件 Y=y1,Y=y2,…,Y=yn 可构成一个完备事件组，即它们两两互不相容，其和为全集。则有：
公式二：

对这个式子左右两侧同时乘以可以得到：
公式三：

根据条件概率的公式我们可以把其中i=1,2,……,n。带入到公式三中，可得到：
公式四：

最终得到的公式四即为全概率公式。我们通常把全概率公式写为一般化形式：

因此对于上面的例子，我们可以根据全概率公式求得：

由题意已知P(男)=2/3,P(女)=1/3（男女比例2:1）最后带入求得P(凉鞋)=5/9,P(非凉鞋)=1-P(凉鞋)=4/9。

后验概率

后验概率是指，某事件 X=x 已经发生，那么该事件是因为事件 Y=y 的而发生的概率。也就是上例中所需要求解的“在知道一个人穿凉鞋的前提下，这个人是男性的概率或者是女性的概率是多少”。后验概率形式化便是：

后验概率的计算要以先验概率为基础。后验概率可以根据通过贝叶斯公式，用先验概率和似然函数计算出来。

贝叶斯公式

根据条件概率公式一，我们可以发现在后验概率和先验概率之间有这样的关系如下。
公式五：

这个公式就是大名鼎鼎的贝叶斯公式，结合一开始给出的例子，根据前面的约定，X=凉鞋，表示穿凉鞋，Y=男，表示男生，该公式即为，穿凉鞋情况下，是男生的概率，正式题目需要我们求的。

现在等式右边所有的数据都是已知的，带入上式即可求得P(男|凉鞋)=3/5,(女|凉鞋)=2/5。

朴素贝叶斯方法的计算过程

朴素贝叶斯分类

朴素贝叶斯分类是一种基于最大后验概率和特征条件独立假设的分类方法，因其思想基础的简单性所以称为朴素：其原理是根据某个对象的先验概率和类条件概率计算其后验概率，然后选择具有最大后验概率的类作为该对象所属的类。
公式如下，对于样本集D:

其中m表示有m个样本， n表示有n个特征(Feature)。y1,y2,..,yk 表示有m个样本类别(Category)，取值为 {C1,C2,…,Ck} 。怎么理解呢，y 我们可以理解为前例中类别男生或者女生，特征可以看成是穿拖鞋或者不穿拖鞋。
由此我们可以分析出已知先验概率分布：
①
还有条件概率分布：
②
在这里朴素贝叶斯法对条件概率的分布做了独立性假设，即假设n个特征值X=X1，X2，……，Xn，在类别确定的前提条件下，n个特征值都是条件独立的，也就是特征值两两互不相关。有了这个假设②式等号右边就可以写成
③
根据贝叶斯公式中先验概率和后验概率的关系：
④
将③式代入④式：

由于对于所有类别都相同，因此这里分母可以省略，可得：
⑤

极大似然法

极大似然估计(Maximum Likelihood Estimation,MLE)是概率论中很常用的估计方法，举一个抛硬币的简单例子来简单说明。现在我们拿到了一枚这种硬币，想试试这硬币是不是均匀的，即想知道抛这枚硬币，正反面出现的概率各是多少？把正面朝上的概率记为θ,那么反面朝上的概率就为1-θ，我们拿这枚硬币抛了10次，正面朝上的结果记为H，反面朝上记为T，抛10次的结果为T,H,H,H,H,T,H,H,H,T。我们想求的正面概率θ \thetaθ是模型参数，而抛硬币模型我们可以假设是二项分布。那么，出现该10次实验的结果x=(T,H,H,H,H,T,H,H,H,T)的似然函数L(x;θ)是多少呢？
抛硬币的似然函数：

其中xi表示第i次试验的结果，正面朝上xi=1，反面朝上xi=0
把10次试验结果带入即可得到注意，这是个只关于θ的函数。而最大似然估计，顾名思义，就是要最大化这个函数。我们可以画出L(x;θ)的图像：

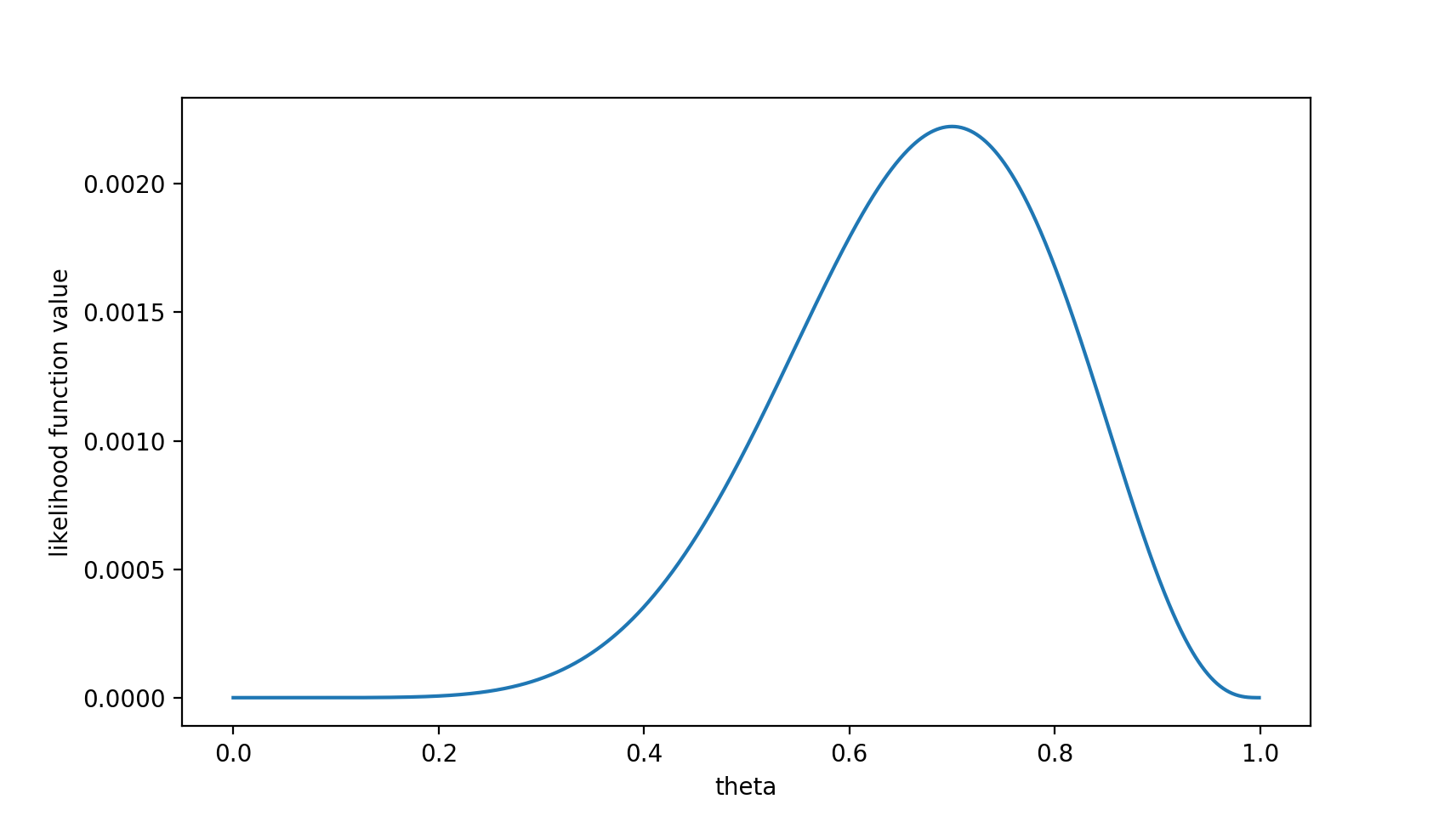
可以看出，在θ=0.7时，似然函数取得最大值。看到这个0.7的数据你可能认为不合理。通常的认知中抛硬币的正反面朝上的概率都应该为0.5。那么究竟是哪里出了问题呢？这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此，引入了最大后验估计。

最大后验估计

极大似然法中是求参数θ, 使似然函数L(x;θ)最大，即P(x | θ)的最大值。而贝叶斯学派认为在试验开始之前，根据人类在生产生活中积累的经验，对未知参数θ已经有了一定的知识，叫做θ的先验知识，先验知识可以用参数θ的某种概率分布来进行表达，记为P(θ)，那么在样本数据集X已知的条件下，再推断参数θ值的概率分布，就是求后验概率P(θ | x)。再带入贝叶斯公式即为求θ使P(x | θ ) P(θ )的值最 大 。 求得的θ不单单让似然函数P(x | θ )大，θ自己出现的先验概率P(θ )也得大。那么参数θ怎么求呢？
在朴素贝叶斯分类器中可以根据极大似然法来写出参数最大后验估计公式，再对似然函数取对数后求导：

最后再利用微积分中求导求最大值的方法来进行求解。

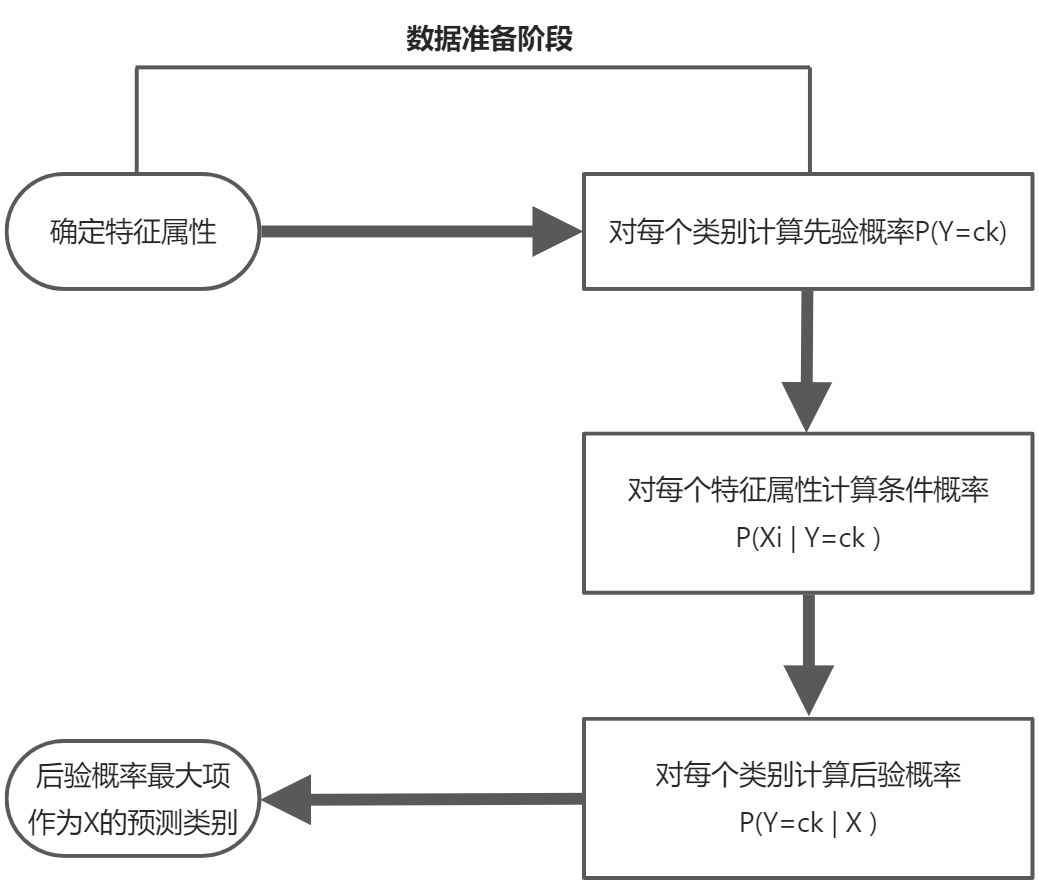
朴素贝叶斯分类的流程

朴素贝叶斯算法分析

优点：

（1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
（2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
（3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

（1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
（2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
（3）由于我们是通过先验概率和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
（4）对输入数据的表达形式很敏感。