决策树(decision tree)是一种基本的分类与回归方法。在分类问题中,表示基于特征对实例进行分类的过程。它可以被看成是if-else规则的集合,也可以认为是定义在特征空间与类空间的条件概率分布。主要特点是模型可解释性强,分类速度快。学习时,利用训练集,根据损失函数最小化原则建立决策树模型。做预测时,在测试集利用模型进行分类。决策树学习主要包括三个步骤:特征选择、决策树的生成和决策树剪枝。
决策树的思想来源于Quinlan于1984年提出来的ID3算法和1993年提出的C4,5算法,以及Breiman等人与1984年提出的CART算法。我们在本章节先介绍决策树基本概念,以及信息熵的相关概念。从讨论如何使用决策树进行训练、可视化和做出预测开始。然后,我们将了解Scikit-Learn使用的CART训练算法,并将讨论如何对树进行正则化并将其用于回归任务。最后,我们将讨论决策树的一些局限性。
6.1 决策树模型
分类决策树模型是一种描述对实例进行分类的树状结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种:内部结点(internal node)和叶子结点(leaf node),其中内部结点表示一个特征或者属性,叶子结点表示一个类。
我们先来通过一个小例子来理解什么是决策树。放暑假了,小明和小亮约了每天下午一起打篮球,但是由于一些原因,有些天他们并没有成行。今天他们把这几天的情况和是否适合打球列了一张表格。
表6-1:打篮球数据集
| ID | 场地 | 温度 | 天气 | 风力 | 是否适合打球 |
|---|---|---|---|---|---|
| 1 | 室内 | 晴天 | 炎热 | 大风 | 适合 |
| 2 | 室内 | 阴天 | 凉爽 | 微风 | 适合 |
| 3 | 室内 | 下雨 | 凉爽 | 大风 | 适合 |
| 4 | 室外 | 阴天 | 凉爽 | 微风 | 适合 |
| 5 | 室外 | 阴天 | 凉爽 | 大风 | 适合 |
| 6 | 室外 | 下雨 | 凉爽 | 大风 | 不适合 |
| 7 | 室外 | 晴天 | 炎热 | 微风 | 不适合 |
| 8 | 室外 | 晴天 | 炎热 | 微风 | 不适合 |
| 9 | 室外 | 晴天 | 凉爽 | 微风 | 适合 |
小明和小亮希望从这张表格中可以找到一个综合各个因素得出是否适合打球的规律,这样今后约球时只需把各个因素输入进去,就知道是否适合打球而不需要纠结思考了。从这个表格中我们分情况判断,很容易得出如下面这个树状图所示的一棵树。
图6-1 打篮球决策树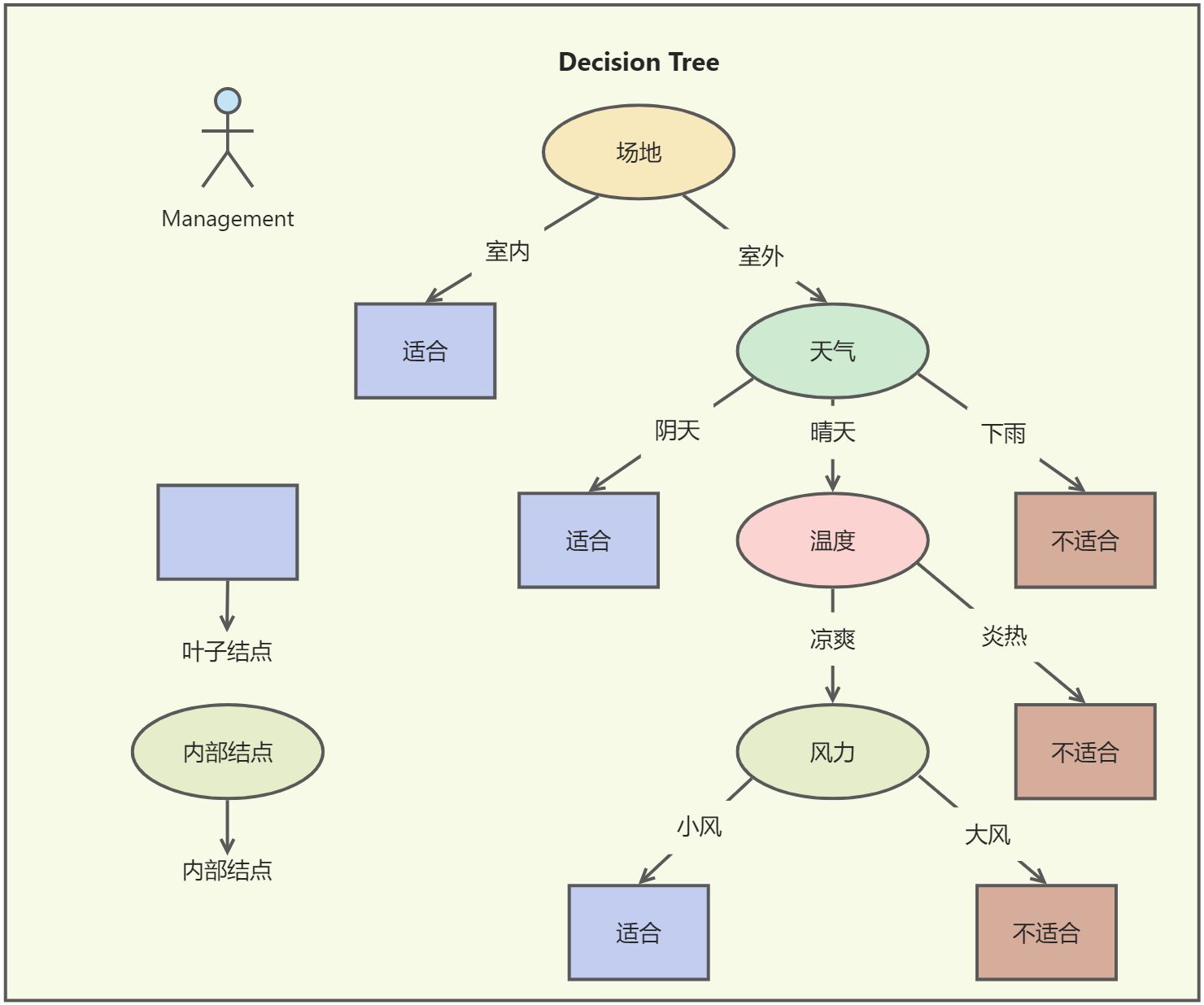
6.1.1决策树与if-else规则
我们可以把上面的树状图理解为Python编程语言条件语句中的if-else语句的集合。现在来观察这棵树。这棵树的节点分为两类,叶子节点和内部节点。
- 每个内部节点都是以某个属性为标准向下分支。
- 每个叶子节点都是一种决策结果。
在这棵决策树中,我们第一个选择的属性是场地,直接帮我们决策了三条数据 (1,2,3), 第二个选择的是天气,又帮我们决策了三条数据(4,5,6)。假设我们没有这样选择,而是第一个选择的风力或者温度,可能这棵树就会复杂很多,我们需要更多条件更多层次才能做出决策。可见在每一个非叶子节点处,选择以哪个属性来划分子树显得格外重要。
我们将决策树转换为if-else规则的过程如下:
- 由决策树的根结点到叶子结点的每一条路径上构建一条规则;
- 路径上内部结点的特征对应着规则的条件,而叶子结点的类对应着规则的结论。
决策树的路径或者其对应的if-else集合具有一个重要的性质:互斥并且完备。这就是说,每一个实例都被一条路径或者规则覆盖且只被一条路径所覆盖
6.1.2 训练和可视化决策树
为了理解决策树,让我们建立一个决策树,然后看看它是如何工作的。
首先导入相关的包并做相应设置:
from sklearn.datasets import load_irisfrom sklearn.tree import DecisionTreeClassifierimport numpy as npimport osimport matplotlib as mplimport matplotlib.pyplot as plt%matplotlib inlinePROJECT_ROOT_DIR = "."CHAPTER_ID = "decision_trees"IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)os.makedirs(IMAGES_PATH, exist_ok=True)
以下代码在鸢尾花数据集上训练了一个DecisionTreeClassifier:
iris = load_iris()X = iris.data[:, 2:] # petal length and widthy = iris.targettree_clf = DecisionTreeClassifier(criterion='entropy',max_depth=3, random_state=42)tree_clf.fit(X, y)iris = load_iris()X = iris.data[:, 2:] # petal length and widthy = iris.target
要将决策树可视化,首先,使用export_graphviz()方法输出一个图形定义文件,命名为iris_tree.dot:
from graphviz import Sourcefrom sklearn.tree import export_graphvizexport_graphviz(tree_clf,out_file=os.path.join(IMAGES_PATH, "iris_tree.dot"),feature_names=iris.feature_names[2:],class_names=iris.target_names,rounded=True,filled=True)Source.from_file(os.path.join(IMAGES_PATH, "iris_tree.dot"))
图6-2显示的是根结点根据特征即花瓣长度进行分类的情形。
这课树的根结点用白色作为底色,叶子结点则用三种不同的颜色作为底色。根据每个节点中的文字内容,我们就可以知道,这个节点选用了哪个属性以及属性值对数据进行再划分,样本量多少,还可以根据节点颜色的深浅来推断类别,不同颜色代表不同类别,颜色深度越浅说明各个类别的混杂程度高,颜色越深说明纯度越高。图6-3中绿、紫、土黄三个颜色就表示了鸢尾花的三种类别。
你可能会产生疑问,为什么图6-2中根结点以花瓣长度是否小于2.45cm来进行分支,Entropy=1.585又代表什么?换句话说就是如何知道一个特征是否具有更好的分类能力呢?于是我们就需要引入熵和信息增益以及包含的数据纯度大小(基尼指数或熵值)等概念,来作为我们选择分类的特征的准则了。
决策树的许多特质之一就是它们几乎不需要数据准备。实际上,它们根本不需要特征缩放或居中。
6.2 信息熵和信息增益
机器学习中,绕不开的一个概念就是熵 (Entropy),信息熵。信息熵常被用来作为一个系统的信息含量的量化指标,从而可以进一步用来作为系统方程优化的目标或者参数选择的判据。在决策树的生成过程中,就使用了熵来作为样本最优属性划分的判据。下面来系统梳理一下有关熵和信息熵的概念。
6.2.1 信息熵的定义
人类对自然世界的认知迈出了三大步:质量、能量和信息量。
人们很早就知道用秤或者天平计量物质的质量,而对能力的认知则是到了19世纪中叶,随着热力学和动力学的发展,以及能量守恒定律的建立才逐渐清楚。能量一词就是热和功的总称,而能量的计量则通过“卡里路、焦耳”等新单位的出现而得到解决。但是信息量是一个非常抽象的概念。比如别人说的一段话就包含某些“信息”,或者我们所看到的一个新闻也包含“信息”,人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一篇 10 万字的论文到底包含多少信息量?信息熵就是用来解决对信息的量化问题的。“熵”这一词语从热力学中借用过来的,热力学中的“热熵”是表示分子状态混乱程度的物理量,信息熵这一概念由克劳德·香农于1948 年提出。香农使用“信息熵”这一概念来量化“信息量”。信息的计算是非常复杂的,具有多重前提条件的信息,更是无法计算,但由于信息熵和热力熵紧密相关,所以信息熵可以在衰减的过程中被测定出来。
信息熵用来表示信息量的大小。为信息论和数字通信奠定了基础。信息熵是用于衡量不确定性的指标,也就是离散随机事件出现的概率,简单地说“情况越混乱,信息熵就越大,反之则越小”。比如,封闭的房间一直不打扫,那么房间不可能越来越干净,只能不断的落灰和结下蜘蛛网,如果想要让它变得整洁、有序就需要外力介入去打扫房间。这个过程中趋向于混乱的房间其信息熵不断增大,而打扫后的房间,则趋向于信息熵最小。伟大数学家香农给出了信息熵的计算公式。
若信号源X的信源符号有n种取值分别为,对应的概率P为
且各个信源符号的出现彼此独立。那么该信源X的平均不确定性,可称为信息熵。
信息熵的定义公式:
6.2.2 信息熵的三个性质
信息论之父克劳德·香农给出的信息熵的三个性质[1]:
- 单调性,发生概率越高的事件,其携带的信息量越低;
- 非负性,信息熵可以看作为一种广度量,非负性是一种合理的必然;
- 累加性,即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和,这也是广度量的一种体现。
香农从数学上严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式:
其中C为常数,我们将其归一化为C=1即得到了信息熵公式。log一般取2或自然对数e为底,如果以2为底,则信息熵的单位为比特(bit),如果以自然对数e为底,则信息熵的单位为纳特(nat)。为什么以2为底?这个数学分析的角度也是极其狭窄:信息是用来消除随机不定性的东西。在香农的眼睛里,信息就是用来表示“有”和“无”的东西。这就是为什么信息的度量是以2为底的log函数。
6.2.3 对信息熵三个性质的理解
单调性说的是,事件发生的概率越低,其发生时所能给出的信息量越大。举一个极端的例子,“太阳从西边升起”所携带的信息量就远大于“太阳从东边升起”,因为后者是一个万年不变的事实,不用特意述说大家都知道;而前者是一个相当不可能发生的事情,如果发生了,那代表了太多的可能性,可能太阳系有重大变故,可能物理法则发生了变化,等等。从某种角度来考虑,单调性也暗含了一种对信息含量的先验假设,即默认某些事实是不含信息量的(默认事实其实也是一种信息,我理解的默认事实应该指的是概率分布),这其实是把默认情况的信息量定标为0了。
对累加性的解释,考虑到信息熵的定义涉及到了事件发生的概率,我们可以假设信息熵是事件发生概率的函数:
对于两个相互独立的事件X=A,Y=B 来说,其同时发生的概率:
其同时发生的信息熵,根据累加性可知:
一种函数形式,满足两个变量乘积函数值等于两个变量函数值的和,那么这种函数形式应该是对数函数。再考虑到概率都是小于等于1的,取对数之后小于0,考虑到信息熵的第二条性质,所以需要在前边加上负号。
6.2.4 回看信息熵定义
回过头来再看信息熵的公式,其中对概率取负对数表示了一种可能事件发生时候携带出的信息量。把各种可能表示出的信息量乘以其发生的概率之后求和,就表示了整个系统所有信息量的一种期望值。从这个角度来说信息熵还可以作为一个系统复杂程度的度量,如果系统越复杂,出现不同情况的种类越多,那么他的信息熵是比较大的。如果一个系统越简单,出现情况种类很少(极端情况为 1种情况,那么对应概率为1,那么对应的信息熵为0),此时的信息熵较小[2]。因此信息熵是度量样本集合纯度最常用的一种指标。信息熵越小,纯度越高。虽然香农的信息概念比以往的认识有了巨大的进步,但仍存在局限性,这一概念同样没有包含信息的内容和价值,只考虑了随机型的不定性,没有从根本上回答”信息是什么”的问题。
事实上,香农最初的动机是把电话中的噪音除掉,他给出通信速率的上限,这个结论首先用在电话上,后来用到光纤,截止2013年又用在无线通信上。我们能够清晰地打越洋电话或卫星电话,都与通信信道质量的改善密切相关。
6.2.5 伯努利分布熵的计算
从熵的定义中可以看出,熵是关于变量X概率分布的函数,而与X的取值没有关系,所以也可以将X 的熵记作 H(p)
熵越大代表随机变量的不确定性越大,当变量可取值的种类一定时,其取每种值的概率分布越平均,其熵值越大。熵的取值范围为:
n 表示取值的种类。
以抛硬币伯努利试验为例,现在对一枚硬币做抛硬币试验,试验结果只有两种即正面和背面,我们把结果为正面记为事件X=1,其概率为p。把结果为背面记为事件X=0,其概率为1-p,其中0<p<1,事件X=1和X=0是独立事件,二者的结果互不影响。那么根据信息熵的定义公式可以得到。抛硬币的信息熵为:
我们在根据p的取值范围(0,1)在坐标轴上画出熵 H(P) 随概率 p变化的曲线如下图所示(单位为比特)
当p=0 或 p=1 时,H(p)=0,随机变量完全没有不确定性。当p=0.5 时,H(p)=1,熵取值最大,随机变量不确定性最大。
6.2.6 两随机变量系统中熵的相关概念
以上介绍了关于单随机变量系统的熵的计算,现实中的系统很多是含有多随机变量的。为了简化问题,以两随机变量系统来说,介绍几个与熵相关的概念。
互信息
两个离散随机变量X 和 Y 的互信息 (Mutual Information) 定义为:
为了理解互信息的涵义,我们把公式中的对数项分解:
我们知道概率取负对数表征了当前概率发生所代表的信息量。上式表明,两事件的互信息为各自事件单独发生所代表的信息量之和减去两事件同时发生所代表的信息量之后剩余的信息量,这表明了两事件单独发生给出的信息量之和是有重复的,互信息度量了这种重复的信息量大小。最后再求概率和表示了两事件互信息量的期望。从式中也可以看出,当两事件完全独立时,p(x,y)=p(x)⋅p(y),互信息计算为0,这也是与常识判断相吻合的。
联合熵
两个离散随机变量X和Y 的联合熵 (Joint Entropy) 为:
联合熵表征了两事件同时发生系统的不确定度。
条件熵
条件熵 (Conditional Entropy),H(Y∣X) 表示在已知随机变量X的条件下随机变量Y的不确定性。
6.2.7 信息增益
当熵和条件熵中的概率由极大似然法得到时,所对应的熵与条件熵分别被称为经验熵(Empirical Entropy)和经验条件熵(Empirical Conditional Entropy)。此时如果有0概率,那么令0log0=0.
信息增益(information gain)表示的是得知特征X的信息而使得类别Y的信息不确定性减少的程度。怎么理解呢?
简单地说,信息增益是针对一个具体的特征而言的,某个特征的有无对于整个系统、集合的影响程度就可以用“信息增益”来描述。我们知道,经过一次 if-else 判别后,原来的类别集合就被被分裂成两个集合,而我们的目的是让其中一个集合的某一类别的“纯度”尽可能高,如果分裂后子集的纯度比原来集合的纯度要高,那就说明这是一次 if-else 划分是有效果的。通过比较使的“纯度”最高的那个划分条件,也就是我们要找的“最合适”的特征维度判别条件。一般而言,信息增益越大,意味着使用特征A来进行划分所带来的纯度提升越大。因此,可以使用信息增益作为准则来进行决策树划分属性的选择,著名的ID3决策树即是如此。
信息增益的定义
信息增益的定义,特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与给定特征A在给定条件下D的经验条件熵H(D|A)之差,即:
经验熵H(D)表示数据集D进行分类的不确定性,而经验条件熵H(D|A)表示在特征A在给定条件下对数据集D进行分类的不确定性,二者之差即为信息增益,表示特征A使得数据集D的分类不确定性减少的程度。显然,对于信息增益大的特征具有更强的分类能力。
信息增益的计算
设训练数据集为D,|D|表示其样本容量, 即样本个数。设有K个类Ck, k = 1,2, …K,|Ck |为属于类Ck的样本个数
特征A有n个不同的 取值{a1,a2…an}根据特征A的取值将D划分为n个子集D1,D2,…… ,Dn,|Di|为 Di的样本个数。
记子集Di中属于类Ck的样本集合为Dik,|Dik|为Dik的样本个数。
输入: 训练数据集D和特征A;
输出: 特征A对训练数据集D的信息增益g(D,A)
(1)计算数据集D的经验熵H(D)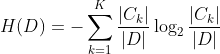
其中K为类别数,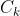 为第k类的样本个数,D为所有类别的样本个数。
为第k类的样本个数,D为所有类别的样本个数。
(2)计算特征A对数据集的经验条件熵H(D|A)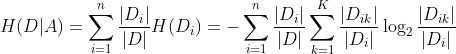
其中,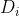 为特征A的取值将D分为n个子集,i=1,…,n,
为特征A的取值将D分为n个子集,i=1,…,n,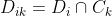 ,即
,即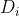 中属于
中属于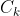 样本的集合。
样本的集合。
(3)计算信息增益
6.2.8 信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。使用信息增益比可以对这一问题进行校正。
信息增益比定义:定义为信息增益与训练数据集D关于特征A的值的熵之比
其中g(D,A)为信息增益,,n是特征值A取值的个数。
6.2.9 基尼指数
CART 决策树采用基尼指数选取最优划分属性。基尼指数的定义:在分类问题中,假设有X个类,样本点位于第x类的概率为Px,那么概率分布的基尼指数定义为:
对于二分类问题,如果样本点属于第1个类别的概率为p,则概率分布基尼指数为:
可以看出,基尼系数反映了随机抽取两个样本,其类别不一致的概率。
与上文类似,分支划分后的基尼系数为各个分支的基尼系数以分支概率为权重进行加和。
6.3 决策树的核心—特征选择
特征选择在于选取对训练数据具有分类能力的特征,可以让划分后的分支数据更有区分性,使各个分支的数据分类纯度更高,最好是每个分支的数据尽可能属于同一类别。根据这个标准,如果找到《计算选择特征前后纯度变化的方法》,那么比较各个选择特征划分纯度变化的大小,选取纯度变化最大的属性来划分分支就行了。选择特征划分纯度变化的计算方法较为典型的有三种:
- 信息增益:在 ID3 决策树中使用
- 信息增益率:在 C4.5 决策树中使用
- 基尼系数:在 CART 决策树中使用
选择特征的方法是决策树的核心。下面我们依次来讨论。
我们以”场地”属性进行划分为例,讨论这三种算法分别如何计算划分前后纯度的变化。(一个属性弄清楚后,依次计算每个属性划分的纯度变化,选择最优的属性划分即可)
下面是我们将用到的”场地”划分的基本数据。
| ID | 场地 | 温度 | 天气 | 风力 | 是否适合打球 |
|---|---|---|---|---|---|
| 1 | 室内 | 晴天 | 炎热 | 大风 | 适合 |
| 2 | 室内 | 阴天 | 凉爽 | 微风 | 适合 |
| 3 | 室内 | 下雨 | 凉爽 | 大风 | 适合 |
| 4 | 室外 | 阴天 | 凉爽 | 微风 | 适合 |
| 5 | 室外 | 阴天 | 凉爽 | 大风 | 适合 |
| 6 | 室外 | 下雨 | 凉爽 | 大风 | 不适合 |
| 7 | 室外 | 晴天 | 炎热 | 微风 | 不适合 |
| 8 | 室外 | 晴天 | 炎热 | 微风 | 不适合 |
| 9 | 室外 | 晴天 | 凉爽 | 微风 | 适合 |
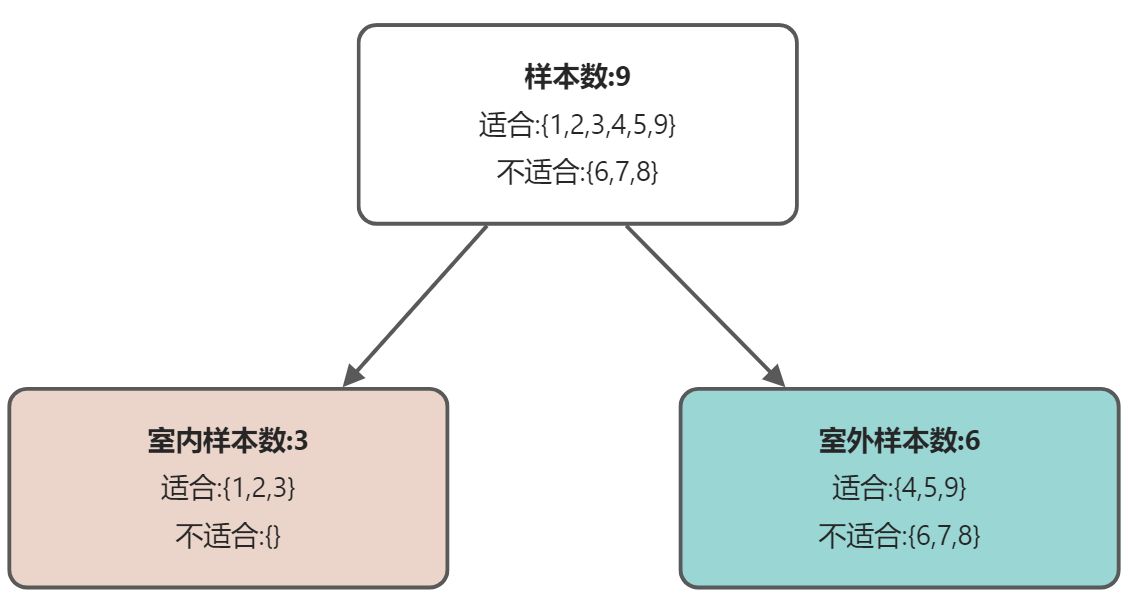
- 划分前: 样本 9
- 适合:{1,2,3,4,5,9},P(适合)=6/9
- 不适合:{6,7,8} P(不适合)=3/9
- 按类别划分后:
- 室外样本 3
- 室内适合:{1,2,3} 联合概率:P(室内,适合)=3/3
- 室内不适合:{} 联合概率:P(室内,适合)=0/3
- 室外样本 6
- 划分之前计算事件的熵:H(X)
- 按照属性 A 划分后再次计算事件的熵:H(X|A)
- 则 g(X,A)=H(X) - H(X|A) 就是划分之后熵被消除了多少。
从我们场地划分的数据,已知P(适合)=6/9,P(不适合)=3/9。根据信息熵的定义公式,场地划分之前的信息熵为:
再计算划分后的条件熵,这一步我们需要先计算条件概率P(X|A),根据条件概率公式:
可以分别求出A=室内和A=室外分别对应的条件概率:
P(X=适合|A=室内)=1,P(X=适合|A=室外)=1/2,P(X=不适合|A=室内)=0,P(X=不适合|A=室外)=1/2。
然后根据条件熵的定义,先分别求出场地为室内和室外两种条件熵:
然后根据求得H(X∣A)=0.2007。
最后根据信息增益的定义求出
我们依次计算各个属性的信息增益然后选择最大的那个属性来划分分支就可以了。
6.3.2 C4.5 算法
C4.5 决策树的方法实际上是在ID3基础上做了改进,C4.5 决策树采用信息增益率选取最优划分属性。之所以改用信息增益率做特征选择是因为信息增益有下列缺陷:
- 如果各个属性的值的个数比较类似,缺陷并不明显
比如:场地{室内、室外},风力{大风、小风},属性值都只有两个
- 如果各个属性的值的个数差异较大,会发现信息增益偏向值个数多的属性
比如:场地{室内、室外},风力{台风、狂风、大风、小风、微风、无风},属性值一个是两个一个是六个
所以为了纠正信息增益偏向值个数多的属性这个缺陷,C4.5 决策树采用了信息增益率。
我们在ID3算法中已经求出了信息增益,现在我们只需求出特征值A的信息熵即可,根据信息熵定义公式求出:
最后求出信息增益比。信息增益率有点矫枉过正,和信息增益相比
- 信息增益偏向值个数多的属性
- 信息增益率偏向值个数少的属性
所以 C4.5 其实并没有直接使用信息增益率,而是先用信息增益选出一些高于平均水平的属性候选集,再从候选集中选出信息增益率最高的属性
6.3.3 CART 算法
CART(classification and regression tree,CART)是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法,是应用广泛的决策树学习方法。
CART算法步骤:
(1)决策树生成:基于训练数据集生成决策树,生成的决策树要尽量大;
(2)决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时用损失函数最小作为剪枝的标准。
CART既可以用于分类又可以用来回归,其中对回归树用平方误差最小化准则,对分类树用基尼指数最小化原则,进行特征选择,生成二叉树。下表列出了三种不同决策树算法的差别:
表6-2 不同决策树算法之间的区别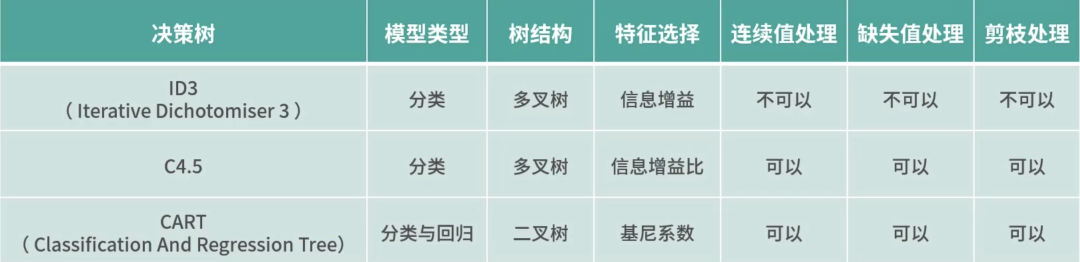
6.4 决策树的生成
根据上述纯度变化的三种不同算法,我们可以选择最优属性开始进行分支,我们通过一段伪代码来看看决策树的构建过程。
决策树构建过程输入:
样本集:DataSet 用 D 表示
属性集:AttributeSet 用 A 表示
决策树构建过程:函数 TreeGenerate(D, A)
- 生成数据原始节点 node # 该节点包含整个输入数据集
- if 样本集数据同属于一个类别,then
将 node 节点标记为叶子节点,构建完成
return
endif - if A 中属性集为空,或 样本集每个样本的每个属性都一样,then
将 node 节点标记为叶子节点, 决策类别为样本个数最多的类别,构建完成
return
endif - 从 A 中选取最优划分属性 aBest:
for aBest 属性上的每个值 aValue:
根据 aValue 生成一个分支节点 branch
- 这个 branch 上的样本集为原样本集的分支子集 DBranch
- 这个 branch 上的属性集为属性集去掉刚刚用过的aBest属性后的属性集 ABranch
if branch 上样本集为空,then
将 branch 标记为叶节点,决策类别为上层样本集中个数最多的类别
else
递归调用 TreeGenerate(DBranch, ABranch)
endif
endfor
容易看出决策树的构建过程是一个属性划分递归的过程,生成决策树的递归过程有三种情形导致递归返回:
- 样本集数据同属于一个类别, 无需划分
- 属性集是空的,或者所有样本所有属性都一样,无法划分
-
6.4.1 连续值的处理
上面打篮球决策树中讨论的特征的值是离散的,如果特征值连续的,比如温度不再是”炎热”和”凉爽”的离散值,而是一个数(比如 1.75),此时应该如何进行属性划分呢?最简单的方法是”二分法”,这也是 C4.5 决策树中采用的机制。
首先找到这个特征在样本集中出现的所有数字并排序,比如有 n 个值,此时连续值变成了每个样本的离散值。
- 排完序的 n 个值在任意两个值中间进行划分,有 n-1 中划分的方法, 比如从第i个与第i+1个之间划分,划分点
.
- 依次计算每个划分点的划分前后区分度(纯度)的变化,选择纯度变化最大的划分点作为该连续特征的划分点,将数据划分为两部分。
6.4.2 CART分类树的生成
从CART算法介绍我们已经知道,CART生成分类树,是用基尼指数选择最优特征后,生成二叉树。如图6-2鸢尾花决策树所示那样,我们看看Scikit-Learn中CART分类树是如何工作的。
首先使用单个特征k和阈值tk(例如,“花瓣长度”≤2.45cm”)将训练集分为两个子集。如何选择k和tk?它搜索产生最纯子集(按其大小加权)的一对(k,tk)下面的公式给出了算法试图最小化的成本函数。
设样本集合D根据特征K取一可能值tk,被分割为D1和D2两部分,则在特征K的条件下
公式:CART分类成本函数:
一旦CART算法成功地将训练集分为两部分,它就会使用相同的逻辑将子集进行分割,然后再分割子集,以此类推。一旦达到最大深度(由超参数max_depth定义),或者找不到可减少不纯度的分割,它将停止递归。其他一些超参数可以控制其他一些停止条件(min_samples_split、min_samples_leaf、min_weight_fraction_leaf和max_leaf_nodes)。
下面我们就用Scikit-Learn中的DecisionTreeClassifier,选择gini指数作为决策函数,生成一颗分类决策树。
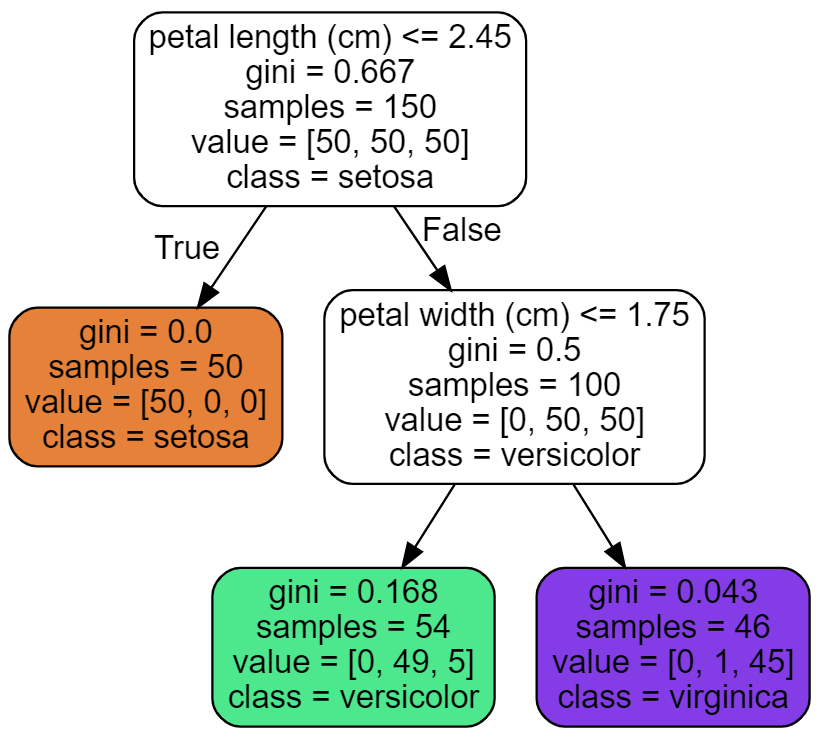
如图6-2中所示。假设你找到一朵鸢尾花,要对其进行分类。你从根节点开始(深度为0,在顶部):该节点询问花的花瓣长度是否小于2.45cm。如果是,则向下移动到根的左子节点(深度1,左侧土黄色)。在这种情况下,它是一片叶子节点(即它没有任何子节点),因此它不会提出任何问题:只需查看该节点的预测类,然后决策树就可以预测花朵是山鸢尾花(class=setosa)。
现在假设你发现了另一朵花,这次花瓣的长度大于2.45cm,你必须向下移动到根的右子节点(深度1,右侧白色),该子节点不是叶子节点,因此该节点会问另一个问题:花瓣宽度是否小于1.75cm?如果是,则你的花朵很可能是变色鸢尾花(深度2,左侧绿色)。如果不是,则可能是维吉尼亚鸢尾花(深度2,右侧紫色)
如你所见,CART是一种贪婪算法:从顶层开始搜索最优分裂,然后每层重复这个过程。几层分裂之后,它并不会检视这个分裂的不纯度是否为可能的最低值。贪婪算法通常会产生一个相当不错的解,但是不能保证是最优解。 而不幸的是,寻找最优树是一个已知的NP完全问题[1]:需要的时间是O(exp(m)),所以即使是很小的训练集,也相当棘手。这就是为什么我们必须接受一个“相当不错”的解。
[1] P是可以在多项式时间内解决的一组问题。NP是可以在多项式时间内验证其解的一组问题。NP难问题是可以在多项式时间内将任何NP问题减少的问题。一个NP完全问题是NP和NP难。一个主要的开放数学问题是P=NP是否相等。如果P≠NP(这似乎是可能的),那么不会找到针对任何NP完全问题的多项式算法(也许在量子计算机上除外)。
6.4.3 CART回归树的生成
让我们使用Scikit-Learn的DecisionTreeRegressor类构建一个回归树,并用max_depth=2在一个有噪声的二次数据集上对其进行训练:
首先构造一个带噪声的数据集
import numpy as npimport osPROJECT_ROOT_DIR = "."CHAPTER_ID = "decision_trees"IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)# Quadratic training set + noisenp.random.seed(42)m = 200X = np.random.rand(m, 1)y = 4 * (X - 0.5) ** 2y = y + np.random.randn(m, 1) / 10
训练决策树回归模型
from sklearn.tree import DecisionTreeRegressortree_reg = DecisionTreeRegressor(criterion='mse',max_depth=2, random_state=42)tree_reg.fit(X, y)
使用export_graphviz()方法将回归决策树可视化
from graphviz import Sourcefrom sklearn.tree import export_graphvizexport_graphviz(tree_reg,out_file=os.path.join(IMAGES_PATH,'tree_reg.dot'),rounded = True, proportion =False,precision = 2, filled = True)Source.from_file(os.path.join(IMAGES_PATH, "tree_reg.dot"))
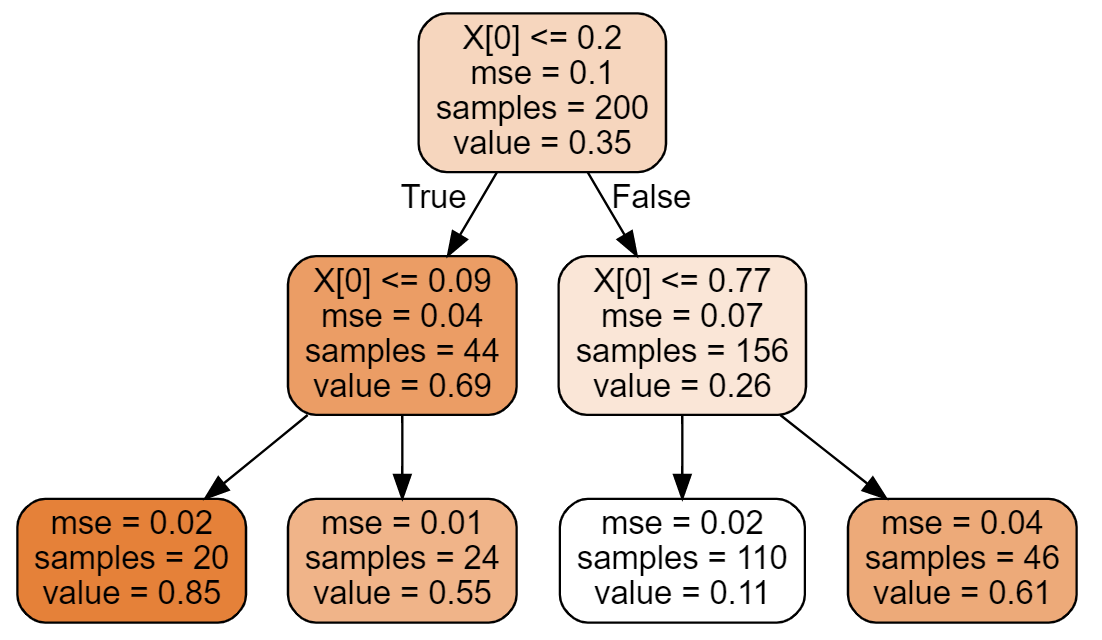
这棵树看起来与之前建立的分类树很相似。主要差别在于,每个节点上不再预测一个类别而是预测一个值。例如,如果你想要对一个x[0]=0.6的新实例进行预测,那么从根节点开始遍历,最后到达预测value=0.11的叶节点。这个预测结果其实就是与这个叶节点关联的110个实例的平均目标值。在这110个实例上,预测产生的均方误差(MSE)等于0.02。
CART用于回归的算法的工作原理与以前的方法大致相同,不同之处在于,它不再尝试以最小化不纯度的方式来拆分训练集,而是以最小化MSE的方式来拆分训练集。公式6-4给出了算法试图最小化的成本函数。
其中即假设样本被划分为m个空间后y^m是Rm上所有实例xi对应输出yi的均值。
图6-5的左侧显示了该模型的预测。如果设置max_depth=3,将得到如图6-5右侧所示的预测。注意看,每个区域的预测值永远等于该区域内实例的目标平均值。算法分裂每个区域的方法就是使最多的训练实例尽可能接近这个预测值。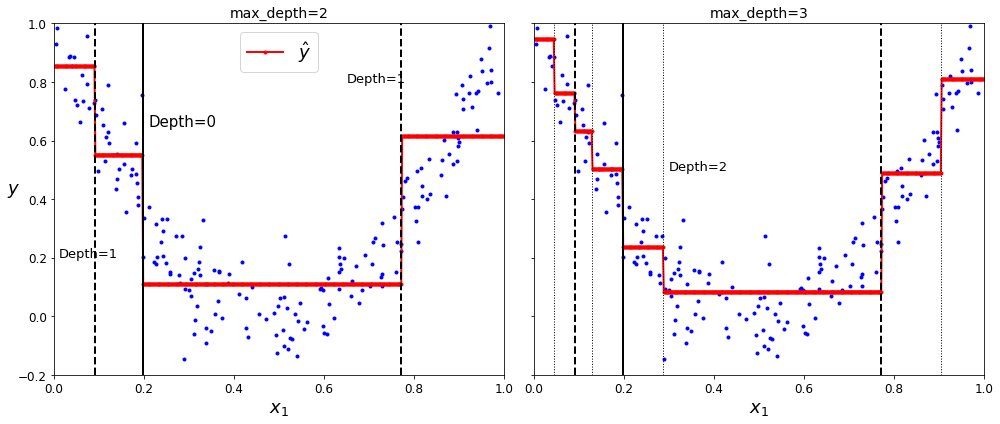
问题是如何对样本进行划分呢?这里就采用启发式的方法:
- 假设第j个变量x(j)和它的取值s,作为切分变量(splitting variable)和切分点(splitting point),并定义两个区域:
- 然后遍历变量j,对固定的切分变量j扫描切分点s,并使得公式6-4达到最小值。
这时即可得出我们定义的两个区域R1和R2中对应的和
。继续对划分后的R1和R2重复这两个步骤。直到将样本空间划分为M个区域即R1,R2,……,Rm,即可完全生成决策树。
6.5 计算复杂度
进行预测需要从根到叶遍历决策树。决策树通常是近似平衡的,因此遍历决策树需要经过大约O(log2(m))个节点(注:log2是二进制对数。它等于log2(m)=log(m)/log(2)。)。由于每个节点仅需要检查一个特征值,因此总体预测复杂度为O(log2(m))。与特征数量无关。因此,即使处理大训练集,预测也非常快。 训练算法比较每个节点上所有样本上的所有特征(如果设置了max_features,则更少)。比较每个节点上所有样本的所有特征会导致训练复杂度为O(n×m log2(m))。对于小训练集(少于几千个实例),Scikit-Learn可以通过对数据进行预排序(设置presort=True)来加快训练速度,但是这样做会大大降低大训练集的训练速度。
6.6 决策树剪枝
决策树生成算法递归地产生决策树,直到不能继续为止。这样产生的树往往对训练数据的分类很准确,决策树极少对训练数据做出假设(比如线性模型就正好相反,它显然假设数据是线性的)。如果不加以限制,树的结构将跟随训练集变化,严密拟合,并且很可能过拟合。这种模型通常被称为非参数模型,这不是说它不包含任何参数(事实上它通常有很多参数),而是指在训练之前没有确定参数的数量,导致模型结构自由而紧密地贴近数据。相反,参数模型(比如线性模型)则有预先设定好的一部分参数,因此其自由度受限,从而降低了过拟合的风险(但是增加了欠拟合的风险)。解决这一问题的办法就是考虑决策树的复杂度,对已经生成的决策树进行简化,我们把这一过程形象地称为剪枝(pruning)。
简单来说就是剪枝就是从已经生成的数上裁掉一些子树或者叶子结点,并将其根结点或父结点作为新的叶子结点,达到简化分类树模型的目的。具体操作则是通过极小化决策树整体的损失函数(loss function)来实现的。
决策树损失函数:
其中C(T)表示模型对训练数据的预测误差,即模型对训练集的拟合程度,|T|表示模型的复杂度,参数α≥0控制两者之间的影响。较大的α促使选择较为简单的决策树模型,较小的α促使选择较为复制的决策树模型。α=0意味着只考虑模型与训练集的拟合程度,不考虑模型复杂度。
在Scikit-Learn中则由设置超参数来实现,决策树的最大深度超参数maxdepth控制(默认值为None,意味着无限制)减小max_depth可使模型更简单,从而降低过拟合的风险。 DecisionTreeClassifier类还有一些其他的参数,同样可以限制决策树的形状:min_samples_split(分裂前节点必须有的最小样本数)、min_samples_leaf(叶节点必须有的最小样本数量)、min_weight_fraction_leaf(与min_samples_leaf一样,但表现为加权实例总数的占比)、max_leaf_nodes(最大叶子节点数量),以及max_features(分裂每个节点评估的最大特征数量)。增大超参数min或减小max_将使模型正则化。
Scikit-Learn还可以先不加约束地训练模型,然后再对不必要的节点进行剪枝(删除)。如果一个节点的子节点全部为叶节点,则该节点可被认为不必要,除非它所表示的纯度提升有重要的统计意义。标准统计测试(比如χ2卡方检验)用来估算“提升纯粹是出于偶然”(被称为零假设)的概率。如果这个概率(称之为p值)高于一个给定阈值(通常是5%,由超参数控制),那么这个节点可被认为不必要,其子节点可被删除。直到所有不必要的节点都被删除,剪枝过程结束。
图6-6显示了在卫星数据集上训练的两个决策树(在第5章中介绍)。左侧使用默认的超参数(即无限制)训练决策树,右侧使用min_samples_leaf=4进行训练。显然,左边的模型过拟合,右边的模型可能会更好地泛化。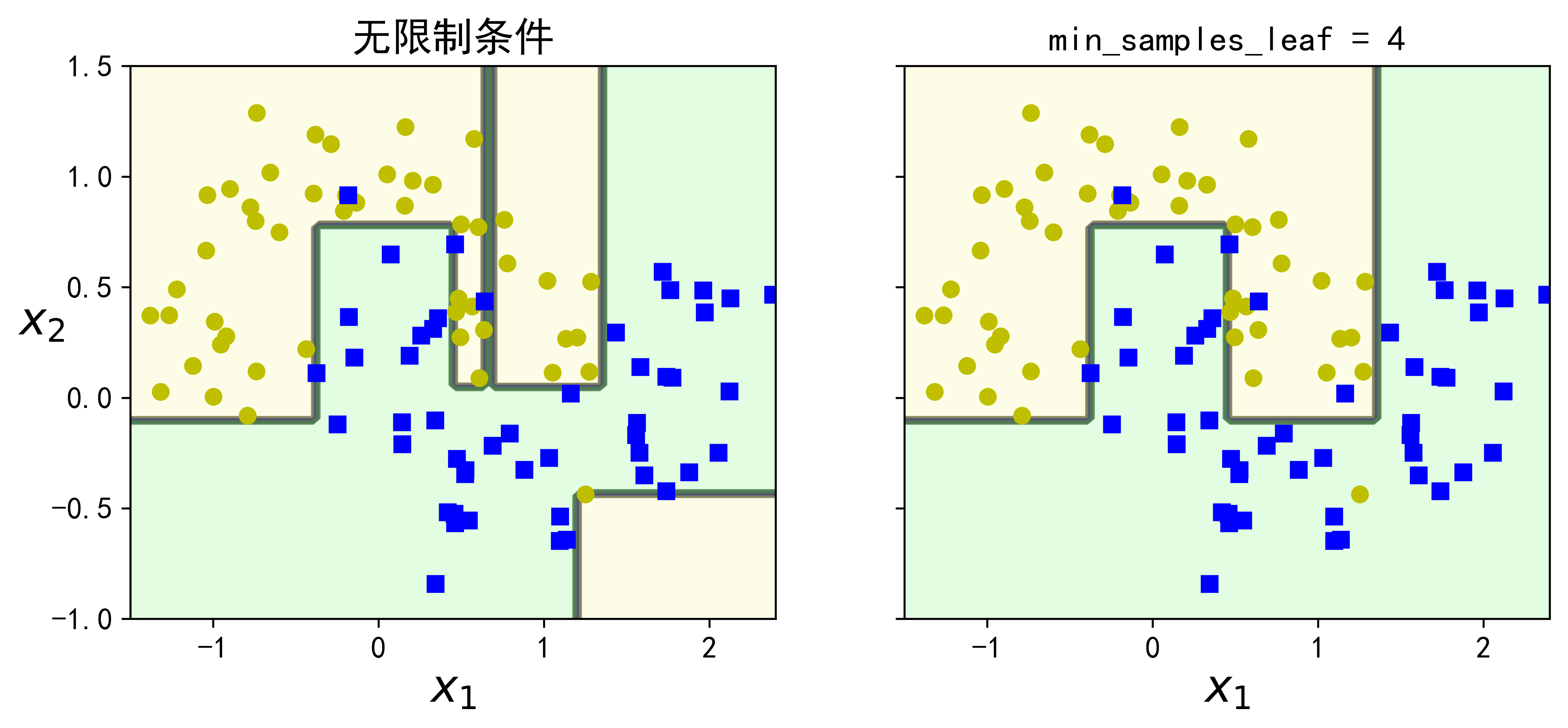
就像分类任务一样,决策树在处理回归任务时容易过拟合。如果不进行任何正则化(如使用默认的超参数),你会得到图6-7左侧的预测。这些预测显然非常过拟合训练集。只需设置min_samples_leaf=10就可以得到一个更合理的模型,如图6-7右侧所示。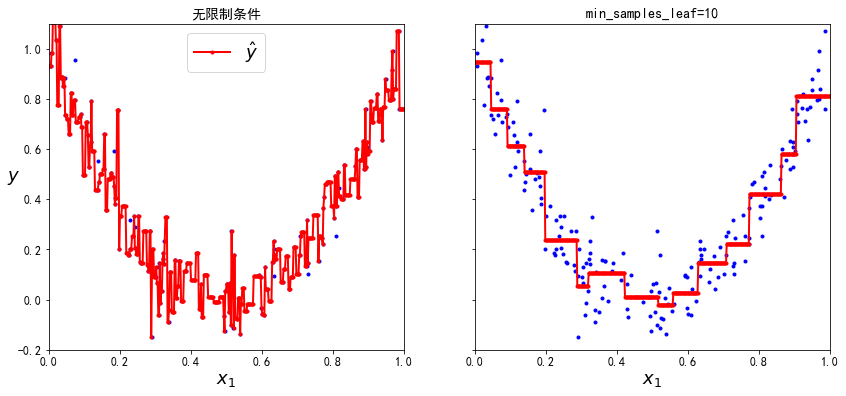
6.7 不稳定性
到目前为止,你已经看到决策树有很多用处:它们易于理解和解释、易于使用、用途广泛且功能强大。但是,它们确实有一些局限性。首先,你可能已经注意到,决策树喜欢正交的决策边界(所有分割都垂直于轴),这使它们对训练集旋转敏感。例如,图6-8显示了一个简单的线性可分离数据集:在左侧,决策树可以轻松地对其进行拆分,而在右侧,将数据集旋转45度后,决策边界看起来复杂了(没有必要)。尽管两个决策树都非常拟合训练集,但右侧的模型可能无法很好地泛化。限制此问题的一种方法是使用主成分分析(见第8章),这通常会使训练数据的方向更好。 
更概括地说,决策树的主要问题是它们对训练数据中的小变化非常敏感。我们来观察下面这个例子:
图6-9显示的是如图6-3基于基尼指数鸢尾花决策树的决策边界。加粗直线表示根节点(深度0)的决策边界:花瓣长度=2.45cm。因为左侧区域是纯的(只有山鸢尾花),所以它不可再分。但是右侧区域是不纯的,所以深度1右侧的节点在花瓣宽度=1.75cm处(虚线所示)再次分裂。因为这里最大深度max_depth设置为2,所以决策树在此停止。但是如果你将max_depth设置为3,那么两个深度为2的节点将各自再产生一条决策边界(点线所示)。 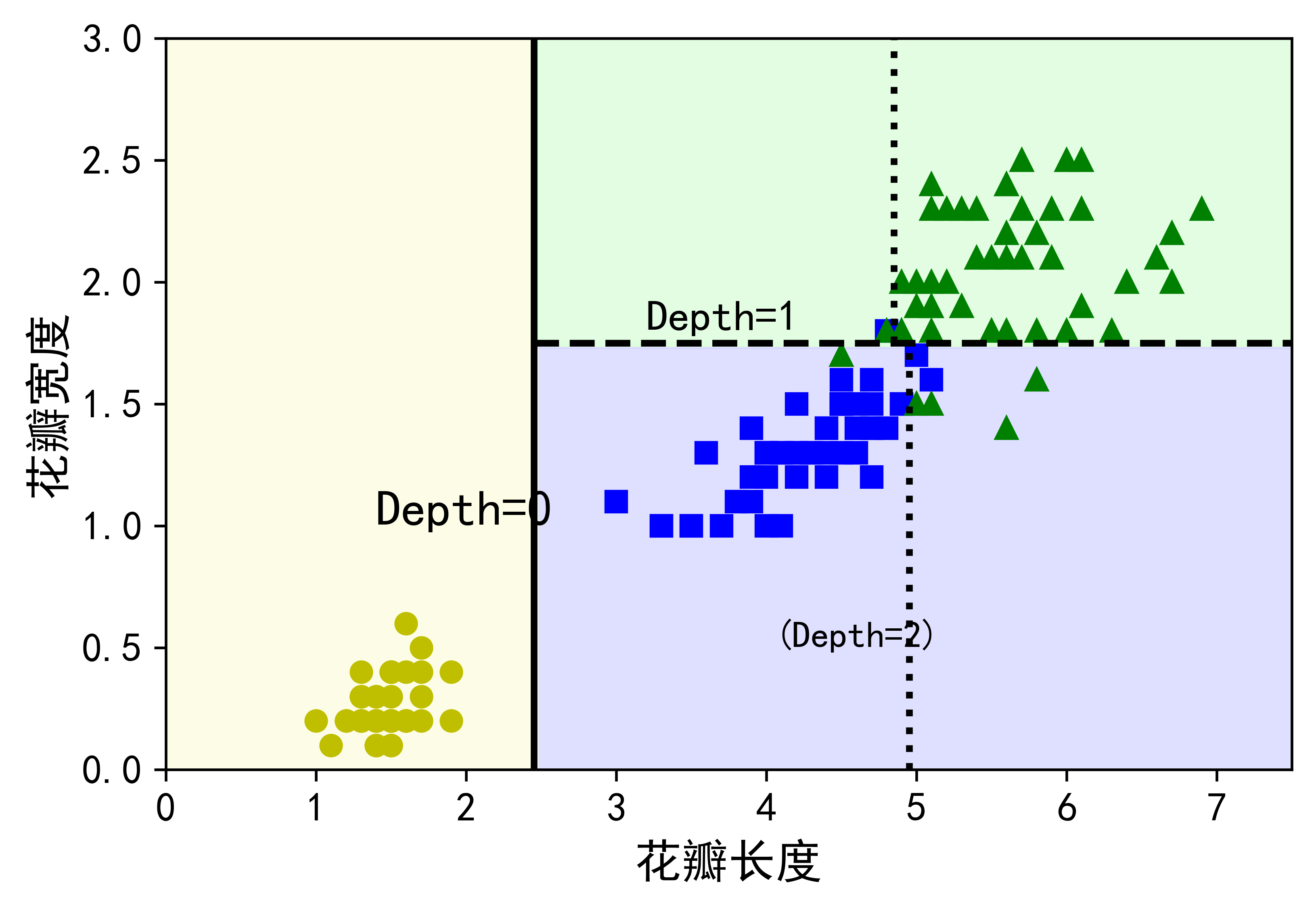
如果你从鸢尾花数据集中移除花瓣最宽的变色鸢尾花(花瓣长4.8cm,宽1.8cm),然后重新训练一个决策树,你可能得到如图6-10所示的模型。这跟之前图6-9的决策树看起来截然不同。事实上,由于Scikit-Learn所使用的算法是随机的[1] ,即使是在相同的训练数据上,你也可能得到完全不同的模型(除非你对超参数random_state进行设置)。
随机森林可以通过对许多树进行平均预测来限制这种不稳定性,正如我们将在第7章中看到的那样。
决策树是直观的,其决策也易于解释。这种模型通常称为白盒模型。相反,正如我们将看到的,通常将随机森林或神经网络视为黑盒模型。它们做出了很好的预测,你可以轻松地检查它们为做出这些预测而执行的计算。但是,通常很难用简单的话语来解释为什么做出这样的预测。例如,如果神经网络说某个人出现在图片上,那么很难知道是什么因素促成了这一预测:该模型识别该人的眼睛、嘴、鼻子、鞋子,甚至他们坐的沙发?相反,决策树提供了很好的、简单的分类规则,如果需要的话,甚至可以手动应用这些规则(例如,用于花的分类)。
[1] 每个节点随机选择特征集进行评估。
6.8 练习题
1.如果训练集有100万个实例,训练决策树(无约束)大致的深度是多少?
2.通常来说,子节点的基尼不纯度是高于还是低于其父节点?是通常更高/更低?还是永远更高/更低?
3.如果决策树过拟合训练集,减少max_depth是否为一个好主意?
4.如果决策树对训练集欠拟合,尝试缩放输入特征是否为一个好主意?
5.如果在包含100万个实例的训练集上训练决策树需要一个小时,那么在包含1000万个实例的训练集上训练决策树,大概需要多长时间?
6.如果训练集包含10万个实例,设置presort=True可以加快训练吗?
7.为卫星数据集训练并微调一个决策树。
- 使用make_moons(n_samples=10000,noise=0.4)生成一个卫星数据集。
- 使用train_test_split()拆分训练集和测试集。
- 使用交叉验证的网格搜索(在GridSearchCV的帮助下)为DecisionTreeClassifier找到适合的超参数。提示:尝试max_leaf_nodes的多种值。
- 使用超参数对整个训练集进行训练,并测量模型在测试集上的性能。你应该得到约85%~87%的准确率。
8.按照以下步骤种植森林。
- 继续之前的练习,生产1000个训练集子集,每个子集包含随机挑选的100个实例。 提示:使用Scikit-Learn的ShuffleSplit来实现。
- 使用前面得到的最佳超参数值,在每个子集上训练一个决策树。在测试集上评估这1000个决策树。因为训练集更小,所以这些决策树的表现可能比第一个决策树要差一些,只能达到约80%的准确率。
- 见证奇迹的时刻到了。对于每个测试集实例,生成1000个决策树的预测,然后仅保留次数最频繁的预测(可以使用SciPy的mode()函数)。这样你在测试集上可获得大多数投票的预测结果。
- 评估测试集上的这些预测,你得到的准确率应该比第一个模型更高(高出0.5%~1.5%)。恭喜,你已经训练出了一个随机森林分类器!

